苏科版数学八年级下册9.4 矩形、菱形、正方形 课件(共19张PPT)
文档属性
| 名称 | 苏科版数学八年级下册9.4 矩形、菱形、正方形 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 12:59:38 | ||
图片预览






文档简介
(共19张PPT)
单/击/此/处/添/加/副/标/题/内/容
9.4矩形、菱形、正方形
温故知新
你还记得菱形的定义与其性质吗?
有一组邻边相等的平行四边形是菱形.(定义)
菱形的四条边相等,对角线互相垂直.(性质定理)
类比探究
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
矩形
对角线相等
一个角是直角
菱形
(定义)
有三个角是直角
类比矩形的判定方法,菱形可能有哪些判定方法呢?
猜想1:
四边相等的四边形是菱形.
猜想2:
对角线互相垂直的平行四边形是菱形.
菱形的判定方法1:有一组邻边相等的平行四边形是菱形.(定义)
猜想
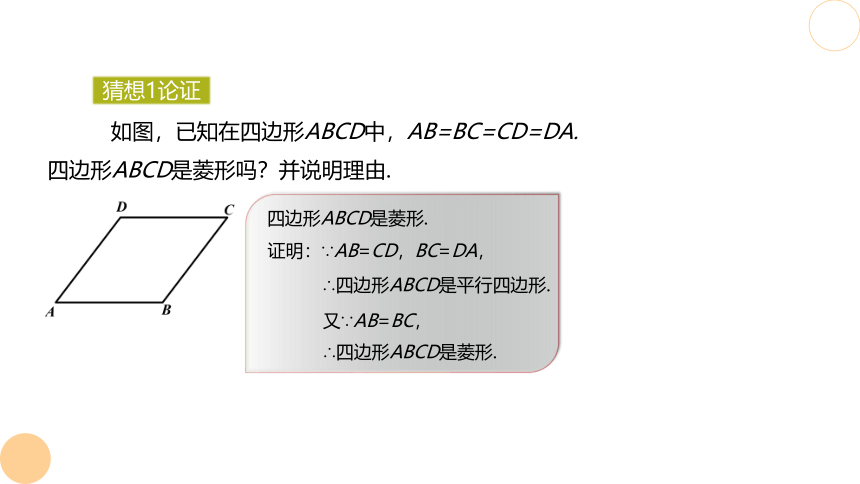
如图,已知在四边形ABCD中,AB=BC=CD=DA.
四边形ABCD是菱形吗?并说明理由.
证明:∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
四边形ABCD是菱形.
猜想1论证
几何语言:
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
菱形的判定方法2 四边相等的四边形是菱形.
猜想2论证
如图,已知在 ABCD中,若AC⊥BD于点O, ABCD是菱形
吗?并说明理由.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,
又∵AC⊥BD,
∴AD=CD,
ABCD是菱形.
∴ ABCD是菱形.
几何语言:
∵在 ABCD中,AC⊥BD,
∴ ABCD是菱形.
菱形的判定方法3 对角线互相垂直的平行四边形是菱形.
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
菱形
对角线垂直
一组邻边相等
(定义)
四边相等
现在你能对刚才视频的猜想进行证明了吗 你有哪些不同的证法?
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
证明方法一:
∴平行四边形ABCD是菱形.
证明方法二:
∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形.
又∵∠1=∠2=∠3=∠4,
∠1+∠2+∠3+∠4=360°,
∴∠1=90°,即AC⊥BD.
你还有其它不同的证法吗?
证明: 如图1,由折叠可知:
∠1=∠2,∠3=∠4,AD=CD,
∵矩形纸片,
∴AD∥BC,
∴∠1=∠4,
∴∠2=∠4,
∴BC=CD,
∴四边形ABCD是菱形.
∴AD=BC,
证明:如图2,由折叠可知:
AO=CO, BO=DO,∠1=∠2,
∴四边形ABCD是平行四边形,
又∵∠1+∠2=180°,
∴∠1=∠2=90°,
∴AC⊥BD,
∴四边形ABCD是菱形.
图1
图2
(视频暂停3 min)
若将视频中“矩形纸片”换成“平行四边形纸片”,结论还成立吗?
将平行四边形纸片ABCD按照如图方式进行折叠,使得点A与点C重合后再展开,折痕与AD、AC、BC分别相交于点E、点O、点F,连接AF和EC.
求证:四边形AFCE是菱形.
1
2
3
想一想
证一证
(视频暂停2 min)
证明:如图,由折叠可知:
AE=EC,∠1=∠2,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴EC=FC,
1
2
3
∴AE=FC,
又∵AE∥FC,
∴四边形AFCE是平行四边形,
∴四边形AFCE是菱形.
若将“证一证”中“平行四边形纸片”换成 “梯形纸片”,结论还成立吗?
由前面的证明可知,结论仍然成立.
想一想
挑战自我
(1)如图1,将一张矩形纸片对折剪开,得到两张长、宽一样大小的矩形纸条,你能利用它们拼出一个菱形吗?
(2)如图2,如果两张矩形的纸片长都是8,宽都是2.那么菱形ABCD的周长、面积是否存在最大值或者最小值?若存在该如何叠放,并分别求出最大值或最小值.
图1
图2
(视频暂停5min)
解:(1)能拼出菱形.
如图3所示:分别过点A、点D作
AE⊥BC于点E,BF⊥CD于点F,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
∵两张矩形纸片的宽度相等,
∴AE=BF,
又∵AE BC=BF CD=
∴BC=CD,
∴平行四边形ABCD是菱形.
图3
(2)存在菱形ABCD的周长、面积最大值与最小值.
①如图4,当∠ABC=90°时,
菱形ABCD的周长与面积同时存在最小值.
周长最小值为8,面积最小值为4.
②如图5,当BD为矩形对角线时,
菱形ABCD的周长与面积同时存在最大值.
设BC=x,在Rt△CDE中,CD2=CE2+DE2,
即 ,
解得 ,
∴菱形ABCD的周长最大值为17,面积最大值为 .
图4
图5
课堂小结
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
矩形
对角线相等
一个角是直角
菱形
(定义)
有三个角是直角
一组邻边相等
(定义)
四边相等
对角线垂直
谢谢观看!
汇报人姓名
单/击/此/处/添/加/副/标/题/内/容
9.4矩形、菱形、正方形
温故知新
你还记得菱形的定义与其性质吗?
有一组邻边相等的平行四边形是菱形.(定义)
菱形的四条边相等,对角线互相垂直.(性质定理)
类比探究
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
矩形
对角线相等
一个角是直角
菱形
(定义)
有三个角是直角
类比矩形的判定方法,菱形可能有哪些判定方法呢?
猜想1:
四边相等的四边形是菱形.
猜想2:
对角线互相垂直的平行四边形是菱形.
菱形的判定方法1:有一组邻边相等的平行四边形是菱形.(定义)
猜想
如图,已知在四边形ABCD中,AB=BC=CD=DA.
四边形ABCD是菱形吗?并说明理由.
证明:∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
四边形ABCD是菱形.
猜想1论证
几何语言:
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
菱形的判定方法2 四边相等的四边形是菱形.
猜想2论证
如图,已知在 ABCD中,若AC⊥BD于点O, ABCD是菱形
吗?并说明理由.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,
又∵AC⊥BD,
∴AD=CD,
ABCD是菱形.
∴ ABCD是菱形.
几何语言:
∵在 ABCD中,AC⊥BD,
∴ ABCD是菱形.
菱形的判定方法3 对角线互相垂直的平行四边形是菱形.
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
菱形
对角线垂直
一组邻边相等
(定义)
四边相等
现在你能对刚才视频的猜想进行证明了吗 你有哪些不同的证法?
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
证明方法一:
∴平行四边形ABCD是菱形.
证明方法二:
∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形.
又∵∠1=∠2=∠3=∠4,
∠1+∠2+∠3+∠4=360°,
∴∠1=90°,即AC⊥BD.
你还有其它不同的证法吗?
证明: 如图1,由折叠可知:
∠1=∠2,∠3=∠4,AD=CD,
∵矩形纸片,
∴AD∥BC,
∴∠1=∠4,
∴∠2=∠4,
∴BC=CD,
∴四边形ABCD是菱形.
∴AD=BC,
证明:如图2,由折叠可知:
AO=CO, BO=DO,∠1=∠2,
∴四边形ABCD是平行四边形,
又∵∠1+∠2=180°,
∴∠1=∠2=90°,
∴AC⊥BD,
∴四边形ABCD是菱形.
图1
图2
(视频暂停3 min)
若将视频中“矩形纸片”换成“平行四边形纸片”,结论还成立吗?
将平行四边形纸片ABCD按照如图方式进行折叠,使得点A与点C重合后再展开,折痕与AD、AC、BC分别相交于点E、点O、点F,连接AF和EC.
求证:四边形AFCE是菱形.
1
2
3
想一想
证一证
(视频暂停2 min)
证明:如图,由折叠可知:
AE=EC,∠1=∠2,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠3,
∴∠2=∠3,
∴EC=FC,
1
2
3
∴AE=FC,
又∵AE∥FC,
∴四边形AFCE是平行四边形,
∴四边形AFCE是菱形.
若将“证一证”中“平行四边形纸片”换成 “梯形纸片”,结论还成立吗?
由前面的证明可知,结论仍然成立.
想一想
挑战自我
(1)如图1,将一张矩形纸片对折剪开,得到两张长、宽一样大小的矩形纸条,你能利用它们拼出一个菱形吗?
(2)如图2,如果两张矩形的纸片长都是8,宽都是2.那么菱形ABCD的周长、面积是否存在最大值或者最小值?若存在该如何叠放,并分别求出最大值或最小值.
图1
图2
(视频暂停5min)
解:(1)能拼出菱形.
如图3所示:分别过点A、点D作
AE⊥BC于点E,BF⊥CD于点F,
∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
∵两张矩形纸片的宽度相等,
∴AE=BF,
又∵AE BC=BF CD=
∴BC=CD,
∴平行四边形ABCD是菱形.
图3
(2)存在菱形ABCD的周长、面积最大值与最小值.
①如图4,当∠ABC=90°时,
菱形ABCD的周长与面积同时存在最小值.
周长最小值为8,面积最小值为4.
②如图5,当BD为矩形对角线时,
菱形ABCD的周长与面积同时存在最大值.
设BC=x,在Rt△CDE中,CD2=CE2+DE2,
即 ,
解得 ,
∴菱形ABCD的周长最大值为17,面积最大值为 .
图4
图5
课堂小结
四边形
平行四边形
一组对边平行且相等
两组对边分别平行
两组对边分别相等
对角线互相平分
矩形
对角线相等
一个角是直角
菱形
(定义)
有三个角是直角
一组邻边相等
(定义)
四边相等
对角线垂直
谢谢观看!
汇报人姓名
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
