苏科版数学八年级下册第九章 中心对称图形——平行四边形 复习课件(共18张PPT)
文档属性
| 名称 | 苏科版数学八年级下册第九章 中心对称图形——平行四边形 复习课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 12:56:25 | ||
图片预览




文档简介
(共18张PPT)
平行四边形小结
从概念到判定
01
02
从一般到特殊
从已知到新探
从概念到判定
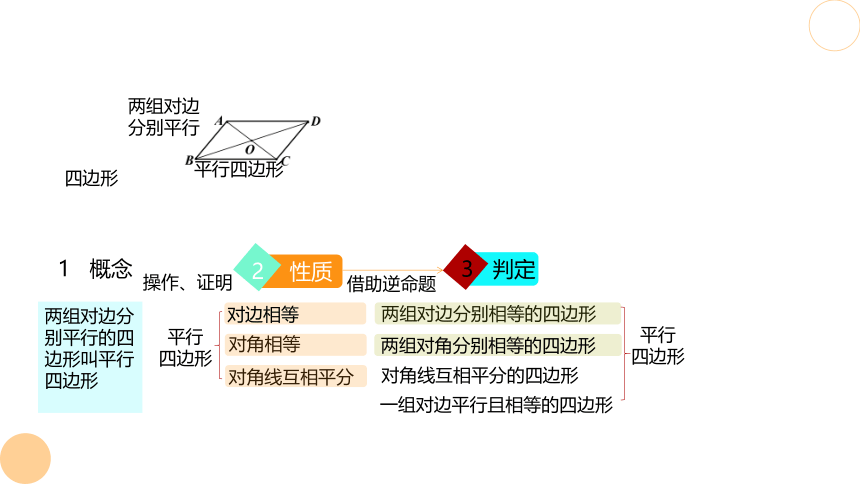
两组对边分别平行
平行四边形
四边形
两组对边分别平行的四边形叫平行四边形
1 概念
2 性质
3 判定
两组对边分别相等的四边形
对角线互相平分的四边形
一组对边平行且相等的四边形
对角相等
对角线互相平分
对边相等
平行
四边形
平行
四边形
操作、证明
借助逆命题
两组对角分别相等的四边形
两组对边分别平行
有一个角是直角的平行四边形叫矩形
矩形
四个角都是直角
对角线相等
矩形
对角线相等的平行四边形
有三个角是直角的四边形
矩形
平行四边形
四边形
有一个角是直角
1 概念
2 性质
3 判定
操作、证明
借助逆命题
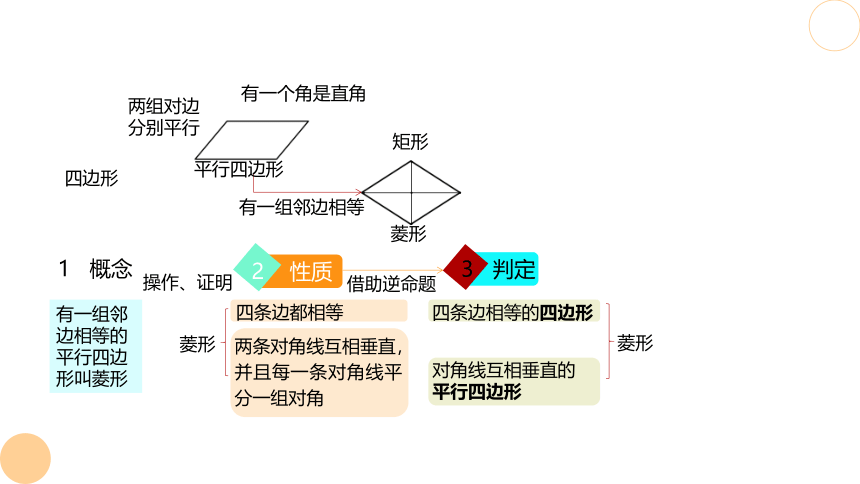
两组对边分别平行
有一组邻边相等的平行四边形叫菱形
菱形
四条边都相等
两条对角线互相垂直,
并且每一条对角线平分一组对角
菱形
对角线互相垂直的
平行四边形
四条边相等的四边形
菱形
四边形
有一组邻边相等
平行四边形
有一个角是直角
矩形
1 概念
2 性质
3 判定
操作、证明
借助逆命题
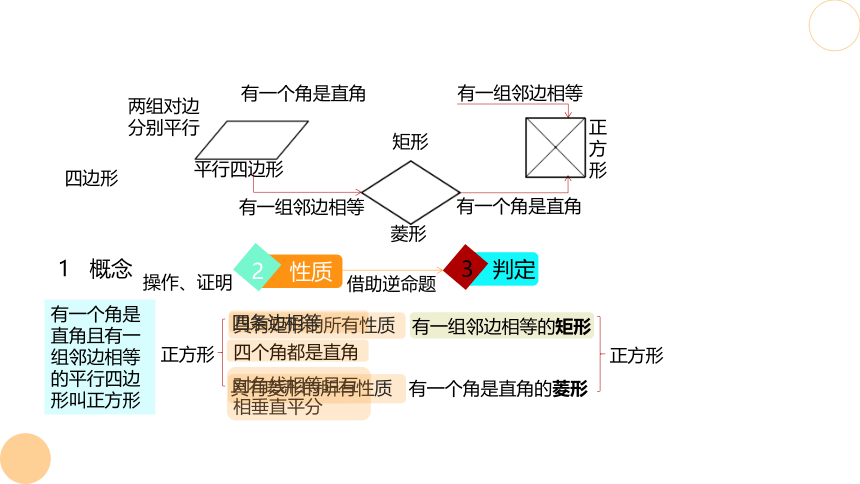
有一个角是直角且有一组邻边相等的平行四边形叫正方形
正方形
具有矩形的所有性质
具有菱形的所有性质
正
方
形
平行四边形
四边形
有一个角是直角
有一组邻边相等
正方形
有一组邻边相等的矩形
有一个角是直角的菱形
两组对边分别平行
矩形
有一个角是直角
有一组邻边相等
菱形
1 概念
2 性质
3 判定
操作、证明
借助逆命题
四个角都是直角
对角线相等且互相垂直平分
四条边相等
平面几何图形的一般研究方法:
1 概念
2 性质
3 判定
操作、证明
借助逆命题
问题1 两组邻边分别相等的四边形叫做筝形.
如图,四边形ABCD中,AB=AD,CB=CD,则四边形ABCD是筝形. 请探究筝形的性质和判定.
一条对角线垂直平分另一条对角线
有一条对角线垂直平分另一条对角线的四边形
有一组对角相等
筝形
有一组对角相等且有一组邻边相等的四边形
筝形
性质:
判定:
从一般到特殊
PART TWO
四边形
平行四边形
矩形
菱形
菱形
矩形
正
方
形
平行四边形
四边形
两组对边分别平行
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
正方形
一般
特殊
【问题1反思】改变筝形ABCD的条件,你会有哪些发现?
问题2 证明中位线定理
已知:如图,△ABC中,点D、E分别是AB、AC的中点.
【分析】 构造平行四边形
当△ABC满足 时,
平行四边形DBCF是
(有一个角是直角的
平行四边形是矩形)
(有一组邻边相等的平行四边形是菱形)
(有一组邻边相等的矩形是正方形)
(有一个角是直角 的矩形是正方形)
矩形.
菱形.
正方形.
∠B=90°
AB=2BC
∠B=90°且AB=2BC
【问题2反思】△ABC形状改变,四边形DBCF的形状随之改变.
从已知到新探
PART THREE
问题3 如图,△ABC中,AD是BC边的中线. 求证:AB+AC>2AD.
证明:延长AD到E,使DE=AD,分别连接BE、CE.
又∵BD=CD,
∴四边形ABEC是平行四边形.
(对角线互相平分的四边形是平行四边形)
∴BE=AC.
在△ABE中
∵AB+BE>AE,
∴AB+AC>2AD.
边
【分析】平行四边形
转
化
小结:
概念
性质
判定
操作、证明
借助逆命题
1.
菱形
矩形
正
方
形
平行四边形
四边形
两组对边分别平行
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
2.
良弓利箭 事半功倍
汇报人姓名
平行四边形小结
从概念到判定
01
02
从一般到特殊
从已知到新探
从概念到判定
两组对边分别平行
平行四边形
四边形
两组对边分别平行的四边形叫平行四边形
1 概念
2 性质
3 判定
两组对边分别相等的四边形
对角线互相平分的四边形
一组对边平行且相等的四边形
对角相等
对角线互相平分
对边相等
平行
四边形
平行
四边形
操作、证明
借助逆命题
两组对角分别相等的四边形
两组对边分别平行
有一个角是直角的平行四边形叫矩形
矩形
四个角都是直角
对角线相等
矩形
对角线相等的平行四边形
有三个角是直角的四边形
矩形
平行四边形
四边形
有一个角是直角
1 概念
2 性质
3 判定
操作、证明
借助逆命题
两组对边分别平行
有一组邻边相等的平行四边形叫菱形
菱形
四条边都相等
两条对角线互相垂直,
并且每一条对角线平分一组对角
菱形
对角线互相垂直的
平行四边形
四条边相等的四边形
菱形
四边形
有一组邻边相等
平行四边形
有一个角是直角
矩形
1 概念
2 性质
3 判定
操作、证明
借助逆命题
有一个角是直角且有一组邻边相等的平行四边形叫正方形
正方形
具有矩形的所有性质
具有菱形的所有性质
正
方
形
平行四边形
四边形
有一个角是直角
有一组邻边相等
正方形
有一组邻边相等的矩形
有一个角是直角的菱形
两组对边分别平行
矩形
有一个角是直角
有一组邻边相等
菱形
1 概念
2 性质
3 判定
操作、证明
借助逆命题
四个角都是直角
对角线相等且互相垂直平分
四条边相等
平面几何图形的一般研究方法:
1 概念
2 性质
3 判定
操作、证明
借助逆命题
问题1 两组邻边分别相等的四边形叫做筝形.
如图,四边形ABCD中,AB=AD,CB=CD,则四边形ABCD是筝形. 请探究筝形的性质和判定.
一条对角线垂直平分另一条对角线
有一条对角线垂直平分另一条对角线的四边形
有一组对角相等
筝形
有一组对角相等且有一组邻边相等的四边形
筝形
性质:
判定:
从一般到特殊
PART TWO
四边形
平行四边形
矩形
菱形
菱形
矩形
正
方
形
平行四边形
四边形
两组对边分别平行
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
正方形
一般
特殊
【问题1反思】改变筝形ABCD的条件,你会有哪些发现?
问题2 证明中位线定理
已知:如图,△ABC中,点D、E分别是AB、AC的中点.
【分析】 构造平行四边形
当△ABC满足 时,
平行四边形DBCF是
(有一个角是直角的
平行四边形是矩形)
(有一组邻边相等的平行四边形是菱形)
(有一组邻边相等的矩形是正方形)
(有一个角是直角 的矩形是正方形)
矩形.
菱形.
正方形.
∠B=90°
AB=2BC
∠B=90°且AB=2BC
【问题2反思】△ABC形状改变,四边形DBCF的形状随之改变.
从已知到新探
PART THREE
问题3 如图,△ABC中,AD是BC边的中线. 求证:AB+AC>2AD.
证明:延长AD到E,使DE=AD,分别连接BE、CE.
又∵BD=CD,
∴四边形ABEC是平行四边形.
(对角线互相平分的四边形是平行四边形)
∴BE=AC.
在△ABE中
∵AB+BE>AE,
∴AB+AC>2AD.
边
【分析】平行四边形
转
化
小结:
概念
性质
判定
操作、证明
借助逆命题
1.
菱形
矩形
正
方
形
平行四边形
四边形
两组对边分别平行
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
2.
良弓利箭 事半功倍
汇报人姓名
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
