苏科版数学八年级下册12.1 二次根式 课件(共17张PPT)
文档属性
| 名称 | 苏科版数学八年级下册12.1 二次根式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 770.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
单/击/此/处/添/加/副/标/题/内/容
二次根式
复 习 回 顾
有理数
整式、分式
加、减、乘、除、乘方、开方
性质
运算
定义
性质
运算
定义
加、减、乘、除、乘方
类
比
开平方
开立方
复 习 回 顾
1. 什么是开平方?
2. 平方根的定义是什么?
求一个数平方根的运算 .
若 x = a(a ≥0),则 x 叫做 a 的平方根 .
正数a 的平方根可以表示为±
叫做 a 的算术平方根.
问 题 情 境
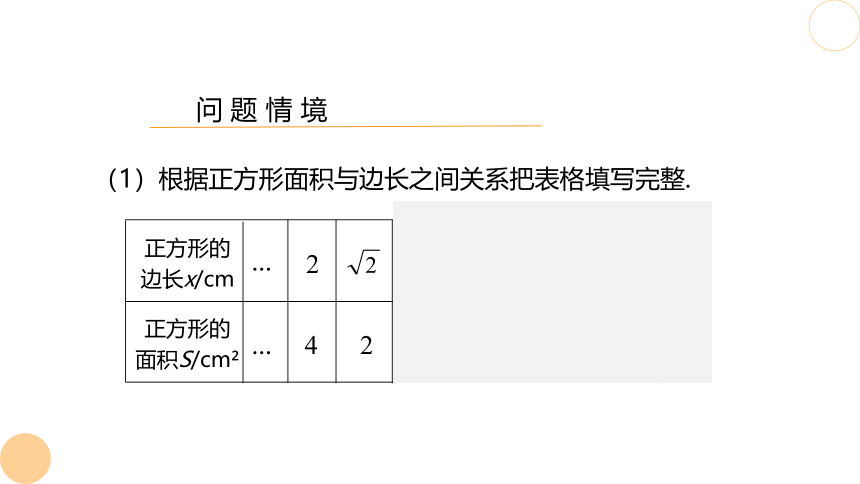
(1)根据正方形面积与边长之间关系把表格填写完整.
正方形的
面积S/cm
正方形的
边长x/cm
…
…
…
…
问 题 情 境
(3)面积为 S 的圆的半径 r 为 .
(2)直角三角形的两条直角边长分别为a、b,则它的
斜边 c 的长为 .
探 究 归 纳
这些式子有什么共同特征?
你能够用一个统一的形式表示这些式子吗?
、
、
、
、
……
、
、
定义 一般地,式子 叫做二次根式,
a 叫做被开方数 .
(a≥0)
概 念 辨 析
下列各式是不是二次根式?
(m≤0)
是
是
是
不是
不是
不是
当 a ≥0 时, 有意义.
知 识 运 用
例1 要使下列各式在实数范围内有意义,x 应是怎样的实数?
解:(1)要使 有意义,必须 x- 5≥0,即 x ≥5 ;
(2)不论 x 取何实数,总有 x ≥0, x + 1≥1,二次
根式 在实数范围内总有意义 .
要使下列各式在实数范围内有意义,x 应是怎样的实数?
解:(1) x ≤ 5 ;
(2) x < 5 .
巩 固 练 习
归 纳 总 结
谈谈对二次根式 的认识 .
性质1
a ≥ 0 ,
≥ 0 .
归 纳 总 结
根据正方形面积与边长之间关系把表格填写完整.
你还能如何理解 ?
“形”
正方形的
面积/cm
正方形的
边长/cm
…
…
…
…
S=2
“数”
是2的算术平方根,由算术平方根的定义可得: =2.
归 纳 总 结
根据正方形面积与边长之间关系把表格填写完整.
2
……
当a≥0时,
性质2
观察这些等式,你能得到什么结论
正方形的
面积/cm
正方形的
边长/cm
…
…
…
…
归 纳 总 结
当a≥0时,
性质2
任何一个非负数的算术平方根的平方就是它本身.
任何一个非负数均可表示为一个数的平方.
当a≥0时,
知 识 运 用
例2 计算:
(a+b≥0).
当a+b≥0时,
解:
巩 固 练 习
1.计算:
解:
拓 展 提 升
2. 在实数范围内分解因式:
初中阶段有三种类型的非负数:① 绝对值;
② 二次根式(算术平方根);③ 偶数次方.
当它们和为0时,必须满足其中的每一项都为0.
1. 若 ,则 = .
总 结 反 思
通过本节课的学习,你有哪些收获?
1. 定义 一般地,式子(a ≥0)叫做二次根式.
2. 性质
性质1
a ≥ 0 ,
≥ 0 .
当a≥0时,
性质2
单/击/此/处/添/加/副/标/题/内/容
二次根式
复 习 回 顾
有理数
整式、分式
加、减、乘、除、乘方、开方
性质
运算
定义
性质
运算
定义
加、减、乘、除、乘方
类
比
开平方
开立方
复 习 回 顾
1. 什么是开平方?
2. 平方根的定义是什么?
求一个数平方根的运算 .
若 x = a(a ≥0),则 x 叫做 a 的平方根 .
正数a 的平方根可以表示为±
叫做 a 的算术平方根.
问 题 情 境
(1)根据正方形面积与边长之间关系把表格填写完整.
正方形的
面积S/cm
正方形的
边长x/cm
…
…
…
…
问 题 情 境
(3)面积为 S 的圆的半径 r 为 .
(2)直角三角形的两条直角边长分别为a、b,则它的
斜边 c 的长为 .
探 究 归 纳
这些式子有什么共同特征?
你能够用一个统一的形式表示这些式子吗?
、
、
、
、
……
、
、
定义 一般地,式子 叫做二次根式,
a 叫做被开方数 .
(a≥0)
概 念 辨 析
下列各式是不是二次根式?
(m≤0)
是
是
是
不是
不是
不是
当 a ≥0 时, 有意义.
知 识 运 用
例1 要使下列各式在实数范围内有意义,x 应是怎样的实数?
解:(1)要使 有意义,必须 x- 5≥0,即 x ≥5 ;
(2)不论 x 取何实数,总有 x ≥0, x + 1≥1,二次
根式 在实数范围内总有意义 .
要使下列各式在实数范围内有意义,x 应是怎样的实数?
解:(1) x ≤ 5 ;
(2) x < 5 .
巩 固 练 习
归 纳 总 结
谈谈对二次根式 的认识 .
性质1
a ≥ 0 ,
≥ 0 .
归 纳 总 结
根据正方形面积与边长之间关系把表格填写完整.
你还能如何理解 ?
“形”
正方形的
面积/cm
正方形的
边长/cm
…
…
…
…
S=2
“数”
是2的算术平方根,由算术平方根的定义可得: =2.
归 纳 总 结
根据正方形面积与边长之间关系把表格填写完整.
2
……
当a≥0时,
性质2
观察这些等式,你能得到什么结论
正方形的
面积/cm
正方形的
边长/cm
…
…
…
…
归 纳 总 结
当a≥0时,
性质2
任何一个非负数的算术平方根的平方就是它本身.
任何一个非负数均可表示为一个数的平方.
当a≥0时,
知 识 运 用
例2 计算:
(a+b≥0).
当a+b≥0时,
解:
巩 固 练 习
1.计算:
解:
拓 展 提 升
2. 在实数范围内分解因式:
初中阶段有三种类型的非负数:① 绝对值;
② 二次根式(算术平方根);③ 偶数次方.
当它们和为0时,必须满足其中的每一项都为0.
1. 若 ,则 = .
总 结 反 思
通过本节课的学习,你有哪些收获?
1. 定义 一般地,式子(a ≥0)叫做二次根式.
2. 性质
性质1
a ≥ 0 ,
≥ 0 .
当a≥0时,
性质2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
