11.1.6 祖暅原理与几何体的体积 教学设计(表格式)
文档属性
| 名称 | 11.1.6 祖暅原理与几何体的体积 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览


文档简介
教学设计
课程基本信息
课题 祖暅原理与几何体的体积
教学目标
1. 了解祖暅原理; 2. 理解柱体、锥体、台体、球体体积公式的产生过程; 3. 体会等价转化的数学思想方法和类比抽象等科学研究方法.
教学内容
教学重点: 理解柱体、锥体、台体、球体的体积公式,并能够运用体积公式求解简单几何体的体积. 教学难点: 利用祖暅原理推导球体体积公式.
教学过程
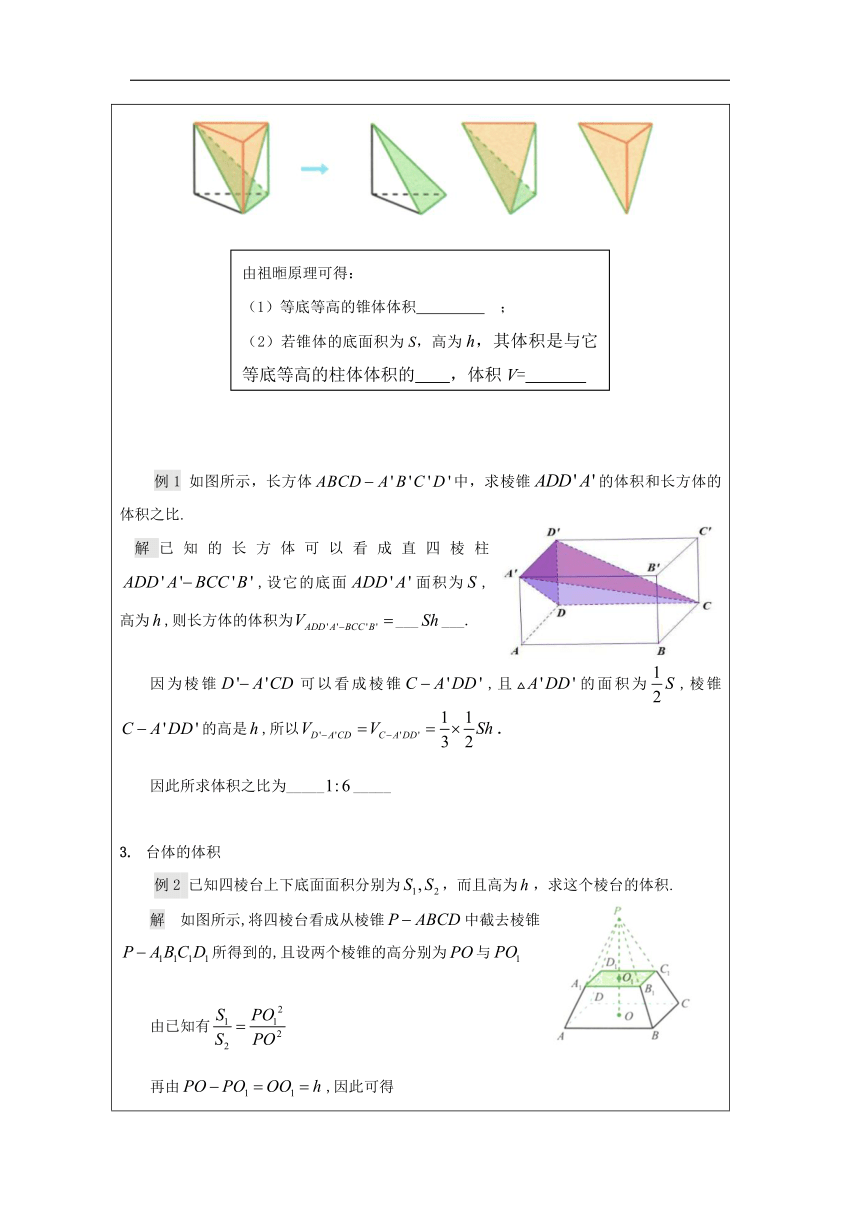
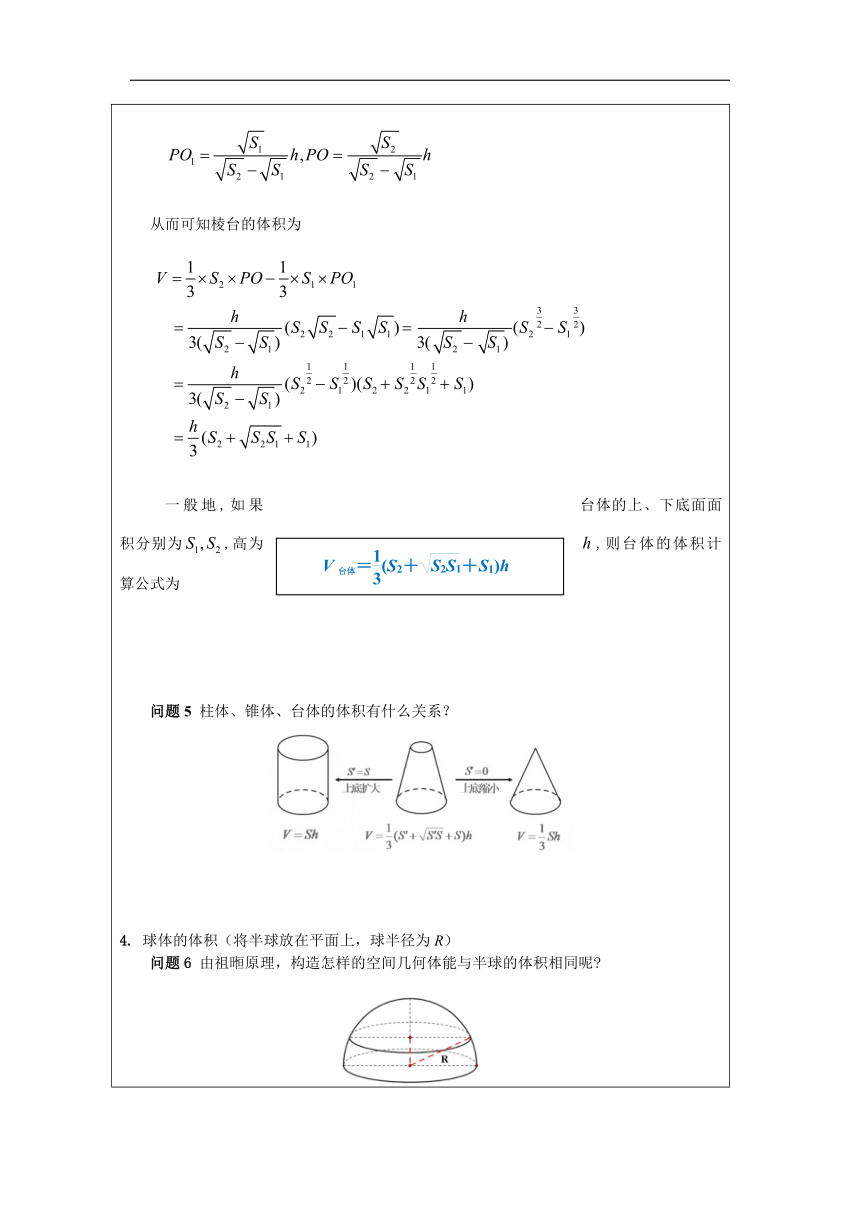
过程一 类比与猜想 问题1 如图所示的矩形与平行四边形面积分别是多少 追问1 对于平面图形中的面积,有怎样一般性的结论 追问2 你能把这一结论推广到空间吗? 过程二 推理与验证 问题2 一摞书本整齐的堆在一起,从外观上可看成什么几何体?体积怎么算? 追问1 把书本朝一个方向推歪了,体积会变化吗?为什么? 追问2 把书本旋转以后,体积会变化吗?为什么? 祖暅原理: 关键词:幂:水平截面面积 势:高 过程三 探究与发现 柱体的体积 问题3 由祖暅原理,等底等高的柱体体积相等吗 追问 柱体转化怎样的特殊几何体求体积呢 2.锥体的体积 问题4 由祖暅原理,等底等高的锥体体积相等吗?为什么 追问1 锥体转化怎样的特殊几何体求体积呢 追问2 能否直接验证棱锥体积是等底等高的棱柱体积的1/3 例1 如图所示,长方体中,求棱锥的体积和长方体的体积之比. 解已知的长方体可以看成直四棱柱,设它的底面面积为,高为,则长方体的体积为______. 因为棱锥可以看成棱锥,且的面积为,棱锥的高是,所以. 因此所求体积之比为__________ 台体的体积 例2 已知四棱台上下底面面积分别为,而且高为,求这个棱台的体积. 解 如图所示,将四棱台看成从棱锥中截去棱锥所得到的,且设两个棱锥的高分别为与 由已知有 再由,因此可得 从而可知棱台的体积为 一般地,如果台体的上、下底面面积分别为,高为,则台体的体积计算公式为 问题5 柱体、锥体、台体的体积有什么关系? 4. 球体的体积(将半球放在平面上,球半径为R) 问题6 由祖暅原理,构造怎样的空间几何体能与半球的体积相同呢 问题7 构造如图所示的圆柱或者圆锥可以吗?为什么 它们的体积之间有怎样的关系? 问题8 将问题7中圆锥倒置在水平桌面上, 用一个与桌面相距为h(0 R)的平面去截半球、圆锥、圆柱,分别求截面面积,你有怎样的发现 问题9 如何构造符合条件的几何体 例3 如图所示,某铁质零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高为2cm,现有这种零件一盒共50kg,取铁的密度为,试估计有多少个这样的零件? 解每个零件的体积为, 因此每个零件的质量为. 因此可以估计出零件的个数为. 例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体.求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可. 过程四 迁移与应用 3.我国南北朝时期的数学家祖暅在计算球的体积时,提出了一个原理(祖暅原理):“幂势既同,则积不容异”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的,几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形。模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为 A. B. C. D. 答案: 1. 2. B 3. B 过程五 总结与提升 问题10 请大家总结这节课在知识、思想和方法上的收获. 知识:柱体、锥体、台体、球体的体积公式 思想:等价转化 方法:类比、抽象 课后练习 教材87页练习A 1~5
课程基本信息
课题 祖暅原理与几何体的体积
教学目标
1. 了解祖暅原理; 2. 理解柱体、锥体、台体、球体体积公式的产生过程; 3. 体会等价转化的数学思想方法和类比抽象等科学研究方法.
教学内容
教学重点: 理解柱体、锥体、台体、球体的体积公式,并能够运用体积公式求解简单几何体的体积. 教学难点: 利用祖暅原理推导球体体积公式.
教学过程
过程一 类比与猜想 问题1 如图所示的矩形与平行四边形面积分别是多少 追问1 对于平面图形中的面积,有怎样一般性的结论 追问2 你能把这一结论推广到空间吗? 过程二 推理与验证 问题2 一摞书本整齐的堆在一起,从外观上可看成什么几何体?体积怎么算? 追问1 把书本朝一个方向推歪了,体积会变化吗?为什么? 追问2 把书本旋转以后,体积会变化吗?为什么? 祖暅原理: 关键词:幂:水平截面面积 势:高 过程三 探究与发现 柱体的体积 问题3 由祖暅原理,等底等高的柱体体积相等吗 追问 柱体转化怎样的特殊几何体求体积呢 2.锥体的体积 问题4 由祖暅原理,等底等高的锥体体积相等吗?为什么 追问1 锥体转化怎样的特殊几何体求体积呢 追问2 能否直接验证棱锥体积是等底等高的棱柱体积的1/3 例1 如图所示,长方体中,求棱锥的体积和长方体的体积之比. 解已知的长方体可以看成直四棱柱,设它的底面面积为,高为,则长方体的体积为______. 因为棱锥可以看成棱锥,且的面积为,棱锥的高是,所以. 因此所求体积之比为__________ 台体的体积 例2 已知四棱台上下底面面积分别为,而且高为,求这个棱台的体积. 解 如图所示,将四棱台看成从棱锥中截去棱锥所得到的,且设两个棱锥的高分别为与 由已知有 再由,因此可得 从而可知棱台的体积为 一般地,如果台体的上、下底面面积分别为,高为,则台体的体积计算公式为 问题5 柱体、锥体、台体的体积有什么关系? 4. 球体的体积(将半球放在平面上,球半径为R) 问题6 由祖暅原理,构造怎样的空间几何体能与半球的体积相同呢 问题7 构造如图所示的圆柱或者圆锥可以吗?为什么 它们的体积之间有怎样的关系? 问题8 将问题7中圆锥倒置在水平桌面上, 用一个与桌面相距为h(0 R)的平面去截半球、圆锥、圆柱,分别求截面面积,你有怎样的发现 问题9 如何构造符合条件的几何体 例3 如图所示,某铁质零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高为2cm,现有这种零件一盒共50kg,取铁的密度为,试估计有多少个这样的零件? 解每个零件的体积为, 因此每个零件的质量为. 因此可以估计出零件的个数为. 例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体.求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可. 过程四 迁移与应用 3.我国南北朝时期的数学家祖暅在计算球的体积时,提出了一个原理(祖暅原理):“幂势既同,则积不容异”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的,几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差.图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形。模仿上述半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为 A. B. C. D. 答案: 1. 2. B 3. B 过程五 总结与提升 问题10 请大家总结这节课在知识、思想和方法上的收获. 知识:柱体、锥体、台体、球体的体积公式 思想:等价转化 方法:类比、抽象 课后练习 教材87页练习A 1~5
