11.1.6 祖暅原理与几何体的体积 课件(共42张PPT)2023-2024学年人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.6 祖暅原理与几何体的体积 课件(共42张PPT)2023-2024学年人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
单/击/此/处/添/加/副/标/题/内/容
祖暅原理与几何体的体积
学习目标
01
02
03
了解祖暅原理;
体会等价转化的数学思想方法和类比抽象等科学研究方法.
理解柱体、锥体、台体、球体积公式的产生过程;
目录/CONTENTS
01
02
03
04
05
06
球
柱体
棱柱
圆柱
锥体
棱锥
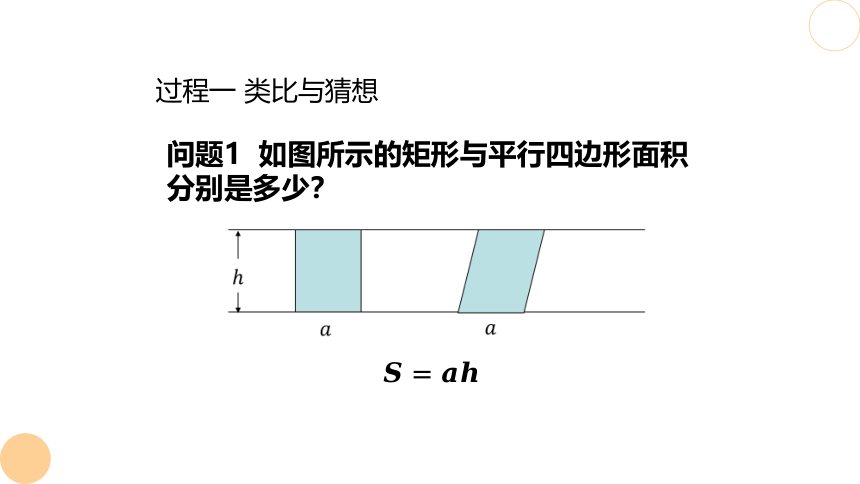
问题1 如图所示的矩形与平行四边形面积分别是多少?
过程一 类比与猜想
追问1 对于等底等高的平行四边形与矩形,有怎样一般性的结论?
过程一 类比与猜想
平行四边形面积
矩形面积
追问2 你能把这一结论推广到空间吗?
等底等高的平行四边形面积相等
实验:取一摞书本堆放在桌面上.
过程二 推理与验证
问题2 一摞书本整齐的堆在一起,从外观上可看成什么几何体?体积怎么算?
长方体体积公式
过程二 推理与验证
追问1 把书本朝一个方向推歪了,体积会变化吗?为什么?
追问2 把书本旋转以后,体积会变化吗?为什么?
过程二 推理与验证
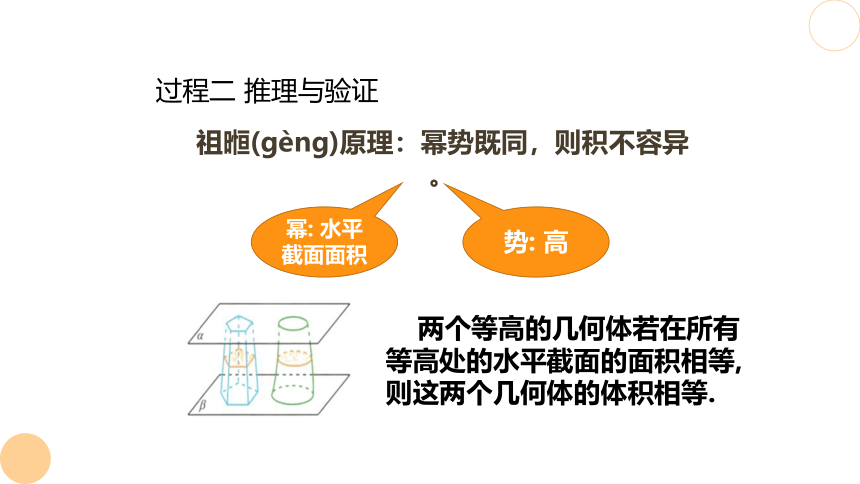
祖暅(gèng)原理:幂势既同,则积不容异。
幂: 水平截面面积
势: 高
两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
过程二 推理与验证
祖暅的介绍:
祖暅是南北朝时期著名数学家祖冲之的儿子. 他从小对数学具有浓厚的兴趣. 祖冲之除了在计算圆周率方面的成就,还与他的儿子祖暅一起,用巧妙的方法解决了柱体,锥体,球体的体积计算. 他们当时采用的原理,在西方被称为“卡瓦列利”原理,但这是在祖氏父子以后一千多年才由意大利数学家卡瓦列利发现的.为了纪念祖氏父子的这一伟大发现,数学上称这个原理为“祖暅原理”.
过程三 探究与发现
1. 柱体的体积
问题3 由祖暅原理,等底等高的柱体体积相等吗?为什么?
追问 柱体转化怎样的几何体求体积呢?
柱体
等底等高的长方体
过程三 探究与发现
由祖暅原理可得:
(1)等底等高的柱体体积_______
(2)若柱体的底面积为S,高为h,则体积V=__________
相等
过程三 探究与发现
2.锥体的体积
问题4 由祖暅原理,等底等高的锥体体积相等吗?为什么?
过程三 探究与发现
追问1 锥体转化为怎样的特殊几何体求体积呢?
追问2 能否直接验证棱锥体积是等底等高的棱柱体
积的1/3?
过程三 探究与发现
等底等高的柱体
锥体
过程三 探究与发现
由祖暅原理可得:
(1)等底等高的锥体体积_______
(2)若锥体的底面积为S,高为h,其体积是与它等底等高的柱体体积的______,体积V=___________
相等
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
3. 台体的体积
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
问题5 柱体、锥体、台体的体积有什么关系?
过程三 探究与发现
4. 球的体积
(将半球放在水平桌面上,球半径为R)
问题6 由祖暅原理,构造怎样的空间几何体能与半球的体积相同呢?
半球体
?
过程三 探究与发现
问题7 构造如图所示的圆柱或者圆锥可以吗?为什么?它们的体积之间有怎样的关系?
R
R
过程三 探究与发现
问题8 将问题7中圆锥倒置在水平桌面上, 用一个与桌面相距为(0 R)的平面去截半球、圆锥、圆柱,分别求截面面积,你有怎样的发现?
过程三 探究与发现
问题9 如何构造符合条件的几何体?
发现:
过程三 探究与发现
实验演示:
1. 拿出圆锥和圆柱
2. 将圆锥倒立放入圆柱
过程三 探究与发现
R
3. 作半球和新的几何体平行于底面的截面
过程三 探究与发现
半球
圆柱与圆锥的组合体
过程三 探究与发现
过程三 探究与发现
由祖暅原理可得:
(1)左右两个几何体体积______
(2)= _____________
则=_______________
相等
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体.求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可.
过程四 迁移与应用
过程四 迁移与应用
过程四 迁移与应用
3. 如图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形。模仿半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为
过程四 迁移与应用
图1 图2
过程四 迁移与应用
过程五 总结与提升
问题10 请大家总结这节课在知识、思想和方法上的收获.
知识:柱体、锥体、台体、球体的体积公式
思想:等价转化
锥体
柱体
长方体
球体
方法:类比、抽象
过程五 总结与提升
课后练习:
教材87页练习A 1~5
谢谢收看
汇报人姓名
单/击/此/处/添/加/副/标/题/内/容
祖暅原理与几何体的体积
学习目标
01
02
03
了解祖暅原理;
体会等价转化的数学思想方法和类比抽象等科学研究方法.
理解柱体、锥体、台体、球体积公式的产生过程;
目录/CONTENTS
01
02
03
04
05
06
球
柱体
棱柱
圆柱
锥体
棱锥
问题1 如图所示的矩形与平行四边形面积分别是多少?
过程一 类比与猜想
追问1 对于等底等高的平行四边形与矩形,有怎样一般性的结论?
过程一 类比与猜想
平行四边形面积
矩形面积
追问2 你能把这一结论推广到空间吗?
等底等高的平行四边形面积相等
实验:取一摞书本堆放在桌面上.
过程二 推理与验证
问题2 一摞书本整齐的堆在一起,从外观上可看成什么几何体?体积怎么算?
长方体体积公式
过程二 推理与验证
追问1 把书本朝一个方向推歪了,体积会变化吗?为什么?
追问2 把书本旋转以后,体积会变化吗?为什么?
过程二 推理与验证
祖暅(gèng)原理:幂势既同,则积不容异。
幂: 水平截面面积
势: 高
两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
过程二 推理与验证
祖暅的介绍:
祖暅是南北朝时期著名数学家祖冲之的儿子. 他从小对数学具有浓厚的兴趣. 祖冲之除了在计算圆周率方面的成就,还与他的儿子祖暅一起,用巧妙的方法解决了柱体,锥体,球体的体积计算. 他们当时采用的原理,在西方被称为“卡瓦列利”原理,但这是在祖氏父子以后一千多年才由意大利数学家卡瓦列利发现的.为了纪念祖氏父子的这一伟大发现,数学上称这个原理为“祖暅原理”.
过程三 探究与发现
1. 柱体的体积
问题3 由祖暅原理,等底等高的柱体体积相等吗?为什么?
追问 柱体转化怎样的几何体求体积呢?
柱体
等底等高的长方体
过程三 探究与发现
由祖暅原理可得:
(1)等底等高的柱体体积_______
(2)若柱体的底面积为S,高为h,则体积V=__________
相等
过程三 探究与发现
2.锥体的体积
问题4 由祖暅原理,等底等高的锥体体积相等吗?为什么?
过程三 探究与发现
追问1 锥体转化为怎样的特殊几何体求体积呢?
追问2 能否直接验证棱锥体积是等底等高的棱柱体
积的1/3?
过程三 探究与发现
等底等高的柱体
锥体
过程三 探究与发现
由祖暅原理可得:
(1)等底等高的锥体体积_______
(2)若锥体的底面积为S,高为h,其体积是与它等底等高的柱体体积的______,体积V=___________
相等
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
3. 台体的体积
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
问题5 柱体、锥体、台体的体积有什么关系?
过程三 探究与发现
4. 球的体积
(将半球放在水平桌面上,球半径为R)
问题6 由祖暅原理,构造怎样的空间几何体能与半球的体积相同呢?
半球体
?
过程三 探究与发现
问题7 构造如图所示的圆柱或者圆锥可以吗?为什么?它们的体积之间有怎样的关系?
R
R
过程三 探究与发现
问题8 将问题7中圆锥倒置在水平桌面上, 用一个与桌面相距为(0 R)的平面去截半球、圆锥、圆柱,分别求截面面积,你有怎样的发现?
过程三 探究与发现
问题9 如何构造符合条件的几何体?
发现:
过程三 探究与发现
实验演示:
1. 拿出圆锥和圆柱
2. 将圆锥倒立放入圆柱
过程三 探究与发现
R
3. 作半球和新的几何体平行于底面的截面
过程三 探究与发现
半球
圆柱与圆锥的组合体
过程三 探究与发现
过程三 探究与发现
由祖暅原理可得:
(1)左右两个几何体体积______
(2)= _____________
则=_______________
相等
过程三 探究与发现
过程三 探究与发现
过程三 探究与发现
例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体.求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可.
过程四 迁移与应用
过程四 迁移与应用
过程四 迁移与应用
3. 如图1是一种“四脚帐篷”的示意图,其中曲线AOC和BOD均是以1为半径的半圆,平面AOC和平面BOD均垂直于平面ABCD,用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形。模仿半球的体积计算方法,可以构造一个与帐篷同底等高的正四棱柱,从中挖去一个倒放的同底等高的正四棱锥(如图2),从而求得该帐篷的体积为
过程四 迁移与应用
图1 图2
过程四 迁移与应用
过程五 总结与提升
问题10 请大家总结这节课在知识、思想和方法上的收获.
知识:柱体、锥体、台体、球体的体积公式
思想:等价转化
锥体
柱体
长方体
球体
方法:类比、抽象
过程五 总结与提升
课后练习:
教材87页练习A 1~5
谢谢收看
汇报人姓名
