2.3.1 圆的标准方程 课件(共31张PPT)2023-2024学年人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.3.1 圆的标准方程 课件(共31张PPT)2023-2024学年人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 16:40:54 | ||
图片预览










文档简介
(共31张PPT)
圆的标准方程
生活中,我们经常接触一些圆形,下面我们就一起来认识一下!
新课引入
完美曲线
01
02
古希腊毕达哥拉斯学派认为圆是平面图形中最美的图形,通过观察这几幅图片,大家能从数学的角度说说为什么吗?
圆 满
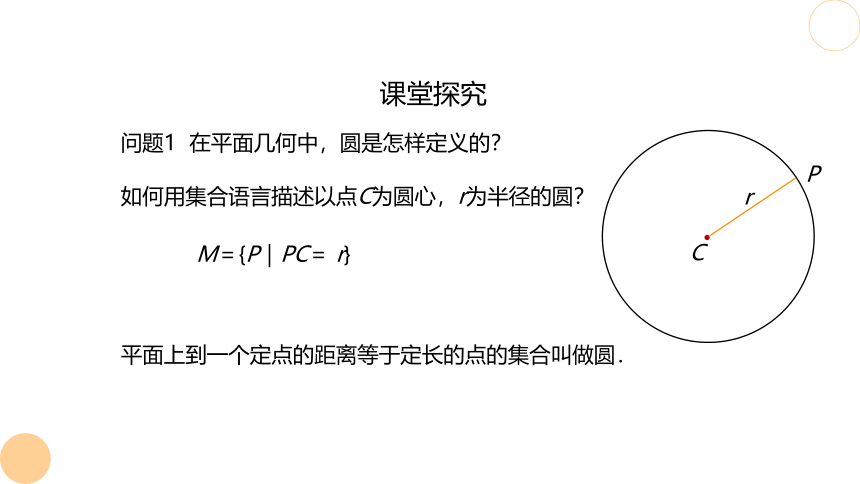
问题1 在平面几何中,圆是怎样定义的?
如何用集合语言描述以点C为圆心,r为半径的圆?
M={P|PC= r}
P
C
r
平面上到一个定点的距离等于定长的点的集合叫做圆.
课堂探究
问题2 在平面几何中,我们学习了圆的哪些主要性质?
(1)圆是轴对称图形,其对称轴是任意一条通过圆心的直线.
圆也是中心对称图形,其对称中心是圆心.
……
(2) 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
(3) 经过切点垂直于切线的直线必经过圆心.
(4) 从圆外一点作圆的两条切线,切线的长相等.
课堂探究
追问:确定一个圆需要哪些条件?
一个圆的圆心位置和半径一旦给定,这个圆就被确定下来了.
课堂探究
用代数的方法研究几何图形的性质
在平面内 在平面直角坐标系中
点 (x,y)
几何 代数
直线 Ax+By+C=0(A2+B2≠0)
圆
课堂探究
学习目标:
理解点在圆上的充要条件;
(2) 根据圆的标准方程,写出圆心,半径;
(3) 会利用条件求圆的标准方程.
圆的标准方程
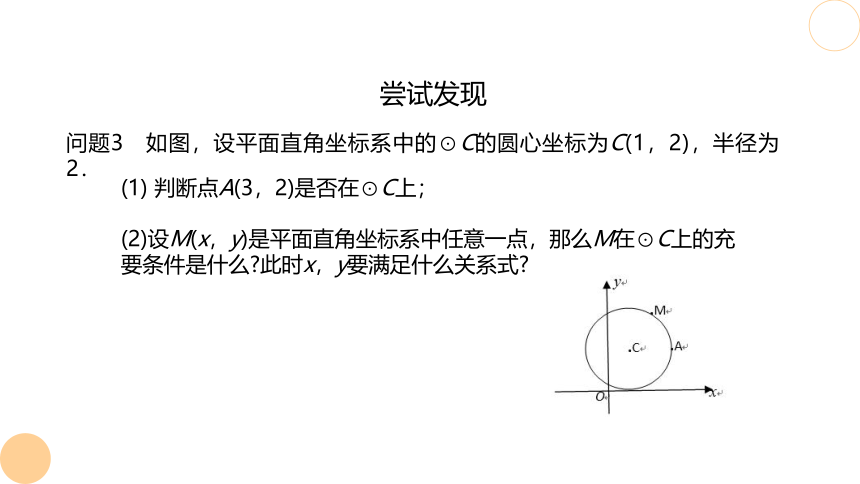
问题3 如图,设平面直角坐标系中的⊙C的圆心坐标为C(1,2),半径为2.
(1) 判断点A(3,2)是否在⊙C上;
(2)设M(x,y)是平面直角坐标系中任意一点,那么M在⊙C上的充要条件是什么 此时x,y要满足什么关系式
尝试发现
尝试发现
追问:一般地,如果⊙C的圆心坐标为C(a,b),而且半径为r(r>0),M(x,y)是平面直角坐标系中任意一点,那么M在⊙C上的充要条件是什么?此时x,y要满足什么关系式?
M(x,y) 在⊙C上的充要条件是|CM|=r,
因此x,y要满足(x-a)2+(y-b)2=r2. ①
尝试发现
(x-a)2+(y-b)2=r2. ①
上述充要条件表明,⊙C上任意一点M(x,y)满足方程①;
如果平面上一点M(x,y)满足方程①,可得|CM|=r,
则点M也在⊙C上.
因此方程①表示以C(a,b)为圆心,r为半径的圆,
①式称为圆的标准方程.
为了方便,我们称圆 (x-a)2+(y-b)2=r2时,
指的是方程为(x-a)2+(y-b)2=r2的圆.
尝试发现
问题4 点M1(x1,y1)在⊙C:(x-a)2+(y-b)2=r2外的充要条件是什么?
(x1-a)2+(y1-b)2>r2
(x2-a)2+(y2-b)2<r2
追问:点M2(x2,y2)在⊙C:(x-a)2+(y-b)2=r2内的充要条件是什么?
尝试发现
问题5 圆的标准方程形式上有什么特点?
圆的标准方程是二元二次方程,无xy项,方程左边是x,y与实数差的平方和;方程的右边是某个非零实数的平方.
含a,b,r三个参数,须有三个独立的条件才能确定一个圆.
若圆心在原点,半径为1,即x2+y2=1称为单位圆.
(x-a)2+(y-b)2=r2
尝试发现
(x-1)2+y2=4 (y≥0)
数学运用
例2 根据下列条件,求圆的标准方程.
(1)圆心在点C(-2,1),且过点A(2,-2);
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
数学运用
(1)圆心在点C(-2,1),且过点A(2,-2);
几何角度:
圆心C(-2,1)
r=|AC|
圆的标准方程
代数角度:
(x+2)2+(y-1)2=r2
代入A点坐标,可得r=5
数学运用
例2 根据下列条件,求圆的标准方程.
代数角度:
设圆方程为(x-a)2+(y-b)2=5
代入A点,B点坐标,求出a,b
数学运用
例2 根据下列条件,求圆的标准方程.
数学运用
例2 根据下列条件,求圆的标准方程.
几何角度:
弦AB中垂线x=1经过圆心,设圆心C(1,b)
数学运用
例2 根据下列条件,求圆的标准方程.
例2 根据下列条件,求圆的标准方程.
数学运用
代数角度:
设圆方程为(x-a)2+(y-b)2=r2
数学运用
例2 根据下列条件,求圆的标准方程.
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
待定系数法
数学运用
例2 根据下列条件,求圆的标准方程.
几何角度:
圆心
在l上
在弦AB中垂线上
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
几何法
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
例3 赵州桥位于我国河北省,是我国现存最早、保存最好的巨大石拱桥.如图赵州桥是一座空腹式的圆弧形石拱桥,利用解析几何的方法,用赵州桥的跨度a和圆拱高b表示出赵州桥圆弧所在圆的半径.
数学运用
x
A
B
y
O
C
D
A
B
例3 赵州桥位于我国河北省,是我国现存最早、保存最好的巨大石拱桥.如图赵州桥是一座空腹式的圆弧形石拱桥,利用解析几何的方法,用赵州桥的跨度a和圆拱高b表示出赵州桥圆弧所在圆的半径.
思考:本题不用解析法怎么解决?
x
y
O
C
D
|OC|.|OD|=|OB|2
△BOC∽△DOB
问题6 求满足下列条件的圆的标准方程:
1.已知A(0,-5),B(0,-1),以线段AB为直径的圆;
2.圆过点(0,1)和(0,3),半径等于1.
课堂检测
问题7 这节课我们学习了什么?请大家总结一下:
知识:①圆的标准方程的推导;
② 判断点与圆的位置关系;
③求圆的标准方程;
(2)方法:求圆的标准方程的两种常用方法:①待定系数法;②几何法;
(3) 思想:数形结合思想.
小结提升
课本第101页练习A第3,5题;练习B第2,3题;
将圆的标准方程展开,我们将会得到什么样的方程?是否所有的这种形式的方程都可以表示成圆的方程?
课后作业
圆的标准方程
生活中,我们经常接触一些圆形,下面我们就一起来认识一下!
新课引入
完美曲线
01
02
古希腊毕达哥拉斯学派认为圆是平面图形中最美的图形,通过观察这几幅图片,大家能从数学的角度说说为什么吗?
圆 满
问题1 在平面几何中,圆是怎样定义的?
如何用集合语言描述以点C为圆心,r为半径的圆?
M={P|PC= r}
P
C
r
平面上到一个定点的距离等于定长的点的集合叫做圆.
课堂探究
问题2 在平面几何中,我们学习了圆的哪些主要性质?
(1)圆是轴对称图形,其对称轴是任意一条通过圆心的直线.
圆也是中心对称图形,其对称中心是圆心.
……
(2) 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
(3) 经过切点垂直于切线的直线必经过圆心.
(4) 从圆外一点作圆的两条切线,切线的长相等.
课堂探究
追问:确定一个圆需要哪些条件?
一个圆的圆心位置和半径一旦给定,这个圆就被确定下来了.
课堂探究
用代数的方法研究几何图形的性质
在平面内 在平面直角坐标系中
点 (x,y)
几何 代数
直线 Ax+By+C=0(A2+B2≠0)
圆
课堂探究
学习目标:
理解点在圆上的充要条件;
(2) 根据圆的标准方程,写出圆心,半径;
(3) 会利用条件求圆的标准方程.
圆的标准方程
问题3 如图,设平面直角坐标系中的⊙C的圆心坐标为C(1,2),半径为2.
(1) 判断点A(3,2)是否在⊙C上;
(2)设M(x,y)是平面直角坐标系中任意一点,那么M在⊙C上的充要条件是什么 此时x,y要满足什么关系式
尝试发现
尝试发现
追问:一般地,如果⊙C的圆心坐标为C(a,b),而且半径为r(r>0),M(x,y)是平面直角坐标系中任意一点,那么M在⊙C上的充要条件是什么?此时x,y要满足什么关系式?
M(x,y) 在⊙C上的充要条件是|CM|=r,
因此x,y要满足(x-a)2+(y-b)2=r2. ①
尝试发现
(x-a)2+(y-b)2=r2. ①
上述充要条件表明,⊙C上任意一点M(x,y)满足方程①;
如果平面上一点M(x,y)满足方程①,可得|CM|=r,
则点M也在⊙C上.
因此方程①表示以C(a,b)为圆心,r为半径的圆,
①式称为圆的标准方程.
为了方便,我们称圆 (x-a)2+(y-b)2=r2时,
指的是方程为(x-a)2+(y-b)2=r2的圆.
尝试发现
问题4 点M1(x1,y1)在⊙C:(x-a)2+(y-b)2=r2外的充要条件是什么?
(x1-a)2+(y1-b)2>r2
(x2-a)2+(y2-b)2<r2
追问:点M2(x2,y2)在⊙C:(x-a)2+(y-b)2=r2内的充要条件是什么?
尝试发现
问题5 圆的标准方程形式上有什么特点?
圆的标准方程是二元二次方程,无xy项,方程左边是x,y与实数差的平方和;方程的右边是某个非零实数的平方.
含a,b,r三个参数,须有三个独立的条件才能确定一个圆.
若圆心在原点,半径为1,即x2+y2=1称为单位圆.
(x-a)2+(y-b)2=r2
尝试发现
(x-1)2+y2=4 (y≥0)
数学运用
例2 根据下列条件,求圆的标准方程.
(1)圆心在点C(-2,1),且过点A(2,-2);
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
数学运用
(1)圆心在点C(-2,1),且过点A(2,-2);
几何角度:
圆心C(-2,1)
r=|AC|
圆的标准方程
代数角度:
(x+2)2+(y-1)2=r2
代入A点坐标,可得r=5
数学运用
例2 根据下列条件,求圆的标准方程.
代数角度:
设圆方程为(x-a)2+(y-b)2=5
代入A点,B点坐标,求出a,b
数学运用
例2 根据下列条件,求圆的标准方程.
数学运用
例2 根据下列条件,求圆的标准方程.
几何角度:
弦AB中垂线x=1经过圆心,设圆心C(1,b)
数学运用
例2 根据下列条件,求圆的标准方程.
例2 根据下列条件,求圆的标准方程.
数学运用
代数角度:
设圆方程为(x-a)2+(y-b)2=r2
数学运用
例2 根据下列条件,求圆的标准方程.
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
待定系数法
数学运用
例2 根据下列条件,求圆的标准方程.
几何角度:
圆心
在l上
在弦AB中垂线上
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
几何法
数学运用
(3)圆心在直线l:2x-7y+8=0上,且过两点A(6,0),B(1,5).
例2 根据下列条件,求圆的标准方程.
例3 赵州桥位于我国河北省,是我国现存最早、保存最好的巨大石拱桥.如图赵州桥是一座空腹式的圆弧形石拱桥,利用解析几何的方法,用赵州桥的跨度a和圆拱高b表示出赵州桥圆弧所在圆的半径.
数学运用
x
A
B
y
O
C
D
A
B
例3 赵州桥位于我国河北省,是我国现存最早、保存最好的巨大石拱桥.如图赵州桥是一座空腹式的圆弧形石拱桥,利用解析几何的方法,用赵州桥的跨度a和圆拱高b表示出赵州桥圆弧所在圆的半径.
思考:本题不用解析法怎么解决?
x
y
O
C
D
|OC|.|OD|=|OB|2
△BOC∽△DOB
问题6 求满足下列条件的圆的标准方程:
1.已知A(0,-5),B(0,-1),以线段AB为直径的圆;
2.圆过点(0,1)和(0,3),半径等于1.
课堂检测
问题7 这节课我们学习了什么?请大家总结一下:
知识:①圆的标准方程的推导;
② 判断点与圆的位置关系;
③求圆的标准方程;
(2)方法:求圆的标准方程的两种常用方法:①待定系数法;②几何法;
(3) 思想:数形结合思想.
小结提升
课本第101页练习A第3,5题;练习B第2,3题;
将圆的标准方程展开,我们将会得到什么样的方程?是否所有的这种形式的方程都可以表示成圆的方程?
课后作业
