4.1.1 条件概率 教学设计(表格式)
文档属性
| 名称 | 4.1.1 条件概率 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 07:31:56 | ||
图片预览



文档简介
教学设计
课程基本信息
课题 4.1.1条件概率
教学目标
1. 结合古典概型,了解条件概率的概念。 2. 结合古典概型,能计算简单随机事件的条件概率。 3.了解条件概率的性质。
教学内容
教学重点: 条件概率概念的理解
教学难点: 条件概率概念的理解
教学过程
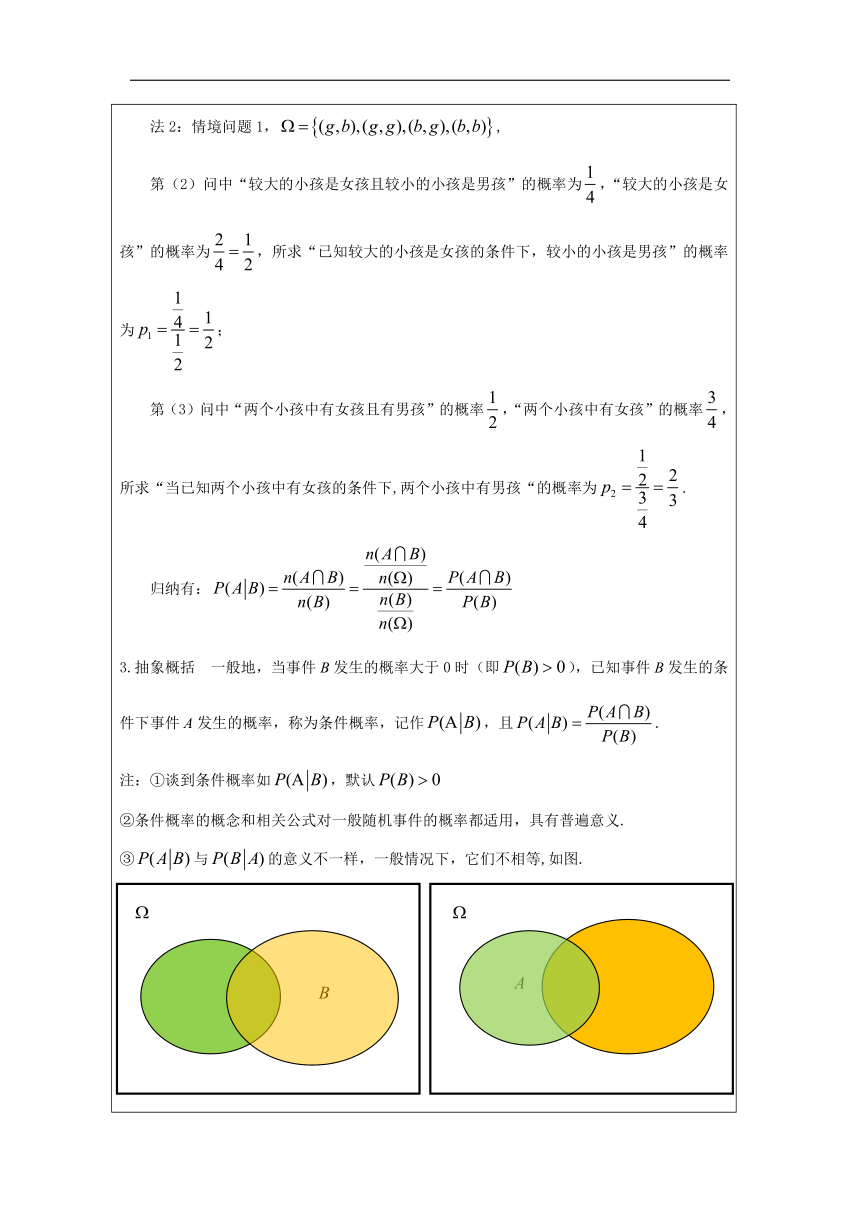
一、情境与问题 1. 金融界的人经常需要计算不同投资环境下获利的概率,因此金融投资公司在招聘新员工时,通常会考查应聘人员计算概率的能力.以下是某金融投资公司的一道笔试题,你会做吗? 从生物学中我们知道,生男、生女的概率基本是相等的,都可以近似地认为是.如果某个家庭中先后生了两个小孩: (1)求两个小孩中有男孩的概率为多少? (2)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少? (3)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少? 2.对于事件A和事件B,当它们互斥时,和事件的概率;当它们不互斥时,有;当它们相互独立时,积事件的概率.当它们不独立时,如何计算呢? 二、尝试与发现 1.问题解答 情境1中的问题:从生物学中我们知道,生男、生女的概率基本是相等的,都可以近似地认为是.如果某个家庭中先后生了两个小孩: (1)求两个小孩中有男孩的概率为多少? (2)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少? (3)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少? 解答:(古典概型)用表示较大的小孩是女孩,较小的小孩是男孩,该试验的样本空间 (1)记“两个小孩中有男孩” 为事件D,,故. (2)记“较大的小孩是女孩” 为事件A,记“较小的小孩是男孩” 为事件B, “已知较大的小孩是女孩的条件下,求较小的小孩是男孩的概率”,相当于以A为样本空间,看事件AB发生的概率, ,故所求概率为. (3)记“两个小孩中有女孩” 为事件C,记“两个小孩中有男孩” 为事件D, “已知两个小孩中有女孩的条件下,求两个小孩中有男孩的概率”,相当于以C为样本空间,看事件CD发生的概率, ,故所求概率为. 指出为什么这里要看“事件AB发生的概率”,“事件CD发生的概率”,便于转化为在样本空间 考虑问题. 2.思考探究 “当已知两个小孩中有女孩的条件下,求两个小孩中有男孩的概率” 这样的概率称为条件概率,记事件“ 两个小孩中有男孩”为事件A,“两个小孩中有女孩”为事件B ,即求已知事件B发生的条件下事件A发生的概率,记作. 一般地,怎样求? 法1:在缩小的样本空间上计算事件的概率. 以B为样本空间,看事件AB发生的概率. 思考:能否利用(不一定全要用到)来求? 法2:情境问题1,, 第(2)问中“较大的小孩是女孩且较小的小孩是男孩”的概率为,“较大的小孩是女孩”的概率为,所求“已知较大的小孩是女孩的条件下,较小的小孩是男孩”的概率为; 第(3)问中“两个小孩中有女孩且有男孩”的概率,“两个小孩中有女孩”的概率,所求“当已知两个小孩中有女孩的条件下,两个小孩中有男孩“的概率为. 归纳有: 3.抽象概括 一般地,当事件B发生的概率大于0时(即),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作,且. 注:①谈到条件概率如,默认 ②条件概率的概念和相关公式对一般随机事件的概率都适用,具有普遍意义. ③与的意义不一样,一般情况下,它们不相等,如图. ④ ;; ⑤公式的变形,及公式的变形回答了情境2中的问题. 三、理解与运用 例1、掷红、蓝两个均匀的骰子,设A:蓝色骰子的点数为5或6;B:两骰子的点数之和大于7.求已知事件A发生的条件下事件B发生的概率. 解:用数对来表示抛掷结果,其中表示红色骰子的点数,表示蓝色骰子的点数,则样本空间可记为,可用图2直观表示,共包含36个样本点. ,包含样本点共12个,则; , 包含样本点共9个, 则; 因此. 答:. 另法:. 小结:1.样本空间及图形表示 2.求条件概率的方法 *3.条件概率与独立性的关系 上例中,,,说明事件A的发生影响了事件B发生的概率。事件A和事件B相互独立的意义是A是否发生不影响B的概率,并用作为事件A和事件B相互独立的定义。可见,上例中事件A和事件B不相互独立。另一方面,如果事件A和事件B相互独立,概率都大于0,则有. 例2、已知某地区内狗的寿命超过15岁的概率为0.8,超过20岁的概率为0.2.那么该地区内,一只寿命超过15岁的狗,寿命能超过20岁的概率为多少? 解:设A:狗的寿命超过15岁,B:狗的寿命超过20岁,则 注意到,所以 所以 答:该地区内,一只寿命超过15岁的狗,寿命能超过20岁的概率为. 四、探索与研究 条件概率的性质 假设A,B,C都是事件,且.根据条件概率的定义,探索条件概率是否满足下列性质:(1); (2); (3)如果B与C互斥,则 证明:(1)法1: 且互斥 又 法2: 同法1 (2) (3)与互斥, 互斥 (
A
) (
C
) (
B
) 五、小结与巩固 小结:1. 时,已知事件B发生的条件下事件A发生的概率,称为条件概率,记作,且. 2. 求, 法1:在缩小的样本空间上计算事件的概率; 法2:. 3.条件概率满足下列性质: (1); (2); (3)如果B与C互斥,则. 课堂练习: 1.一个袋子里有10个球(除颜色外其他属性都相同),其中4个红球,6个白。甲、乙两人依次不放回地摸取1个球,在甲摸到红球的情况下,乙摸到红球的概率为( ) A. B. C. D. 【答案】A 【详解】在缩小的样本空间上考虑条件概率,甲先摸到1个红球,乙再从剩下的9个球中摸1个球,共有种,其中甲先摸到1个红球,乙再从剩下的3个红球中摸1个球,共有种.所以在甲摸到红球的情况下,乙摸到红球的概率为.故选:A. 2.已知春季里,每天甲、乙两地下雨的概率分别为20%与18%,且两地同时下雨的概率为12%.求春季的一天里: (1)已知甲地下雨的条件下,乙地也下雨的概率; (2)已知乙地下雨的条件下,甲地也下雨的概率. 解:则为 (1) (2) 答:(1)春季的一天里已知甲地下雨的条件下,乙地也下雨的概率为; (2)春季的一天里已知乙地下雨的条件下,甲地也下雨的概率为.
课程基本信息
课题 4.1.1条件概率
教学目标
1. 结合古典概型,了解条件概率的概念。 2. 结合古典概型,能计算简单随机事件的条件概率。 3.了解条件概率的性质。
教学内容
教学重点: 条件概率概念的理解
教学难点: 条件概率概念的理解
教学过程
一、情境与问题 1. 金融界的人经常需要计算不同投资环境下获利的概率,因此金融投资公司在招聘新员工时,通常会考查应聘人员计算概率的能力.以下是某金融投资公司的一道笔试题,你会做吗? 从生物学中我们知道,生男、生女的概率基本是相等的,都可以近似地认为是.如果某个家庭中先后生了两个小孩: (1)求两个小孩中有男孩的概率为多少? (2)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少? (3)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少? 2.对于事件A和事件B,当它们互斥时,和事件的概率;当它们不互斥时,有;当它们相互独立时,积事件的概率.当它们不独立时,如何计算呢? 二、尝试与发现 1.问题解答 情境1中的问题:从生物学中我们知道,生男、生女的概率基本是相等的,都可以近似地认为是.如果某个家庭中先后生了两个小孩: (1)求两个小孩中有男孩的概率为多少? (2)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少? (3)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少? 解答:(古典概型)用表示较大的小孩是女孩,较小的小孩是男孩,该试验的样本空间 (1)记“两个小孩中有男孩” 为事件D,,故. (2)记“较大的小孩是女孩” 为事件A,记“较小的小孩是男孩” 为事件B, “已知较大的小孩是女孩的条件下,求较小的小孩是男孩的概率”,相当于以A为样本空间,看事件AB发生的概率, ,故所求概率为. (3)记“两个小孩中有女孩” 为事件C,记“两个小孩中有男孩” 为事件D, “已知两个小孩中有女孩的条件下,求两个小孩中有男孩的概率”,相当于以C为样本空间,看事件CD发生的概率, ,故所求概率为. 指出为什么这里要看“事件AB发生的概率”,“事件CD发生的概率”,便于转化为在样本空间 考虑问题. 2.思考探究 “当已知两个小孩中有女孩的条件下,求两个小孩中有男孩的概率” 这样的概率称为条件概率,记事件“ 两个小孩中有男孩”为事件A,“两个小孩中有女孩”为事件B ,即求已知事件B发生的条件下事件A发生的概率,记作. 一般地,怎样求? 法1:在缩小的样本空间上计算事件的概率. 以B为样本空间,看事件AB发生的概率. 思考:能否利用(不一定全要用到)来求? 法2:情境问题1,, 第(2)问中“较大的小孩是女孩且较小的小孩是男孩”的概率为,“较大的小孩是女孩”的概率为,所求“已知较大的小孩是女孩的条件下,较小的小孩是男孩”的概率为; 第(3)问中“两个小孩中有女孩且有男孩”的概率,“两个小孩中有女孩”的概率,所求“当已知两个小孩中有女孩的条件下,两个小孩中有男孩“的概率为. 归纳有: 3.抽象概括 一般地,当事件B发生的概率大于0时(即),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作,且. 注:①谈到条件概率如,默认 ②条件概率的概念和相关公式对一般随机事件的概率都适用,具有普遍意义. ③与的意义不一样,一般情况下,它们不相等,如图. ④ ;; ⑤公式的变形,及公式的变形回答了情境2中的问题. 三、理解与运用 例1、掷红、蓝两个均匀的骰子,设A:蓝色骰子的点数为5或6;B:两骰子的点数之和大于7.求已知事件A发生的条件下事件B发生的概率. 解:用数对来表示抛掷结果,其中表示红色骰子的点数,表示蓝色骰子的点数,则样本空间可记为,可用图2直观表示,共包含36个样本点. ,包含样本点共12个,则; , 包含样本点共9个, 则; 因此. 答:. 另法:. 小结:1.样本空间及图形表示 2.求条件概率的方法 *3.条件概率与独立性的关系 上例中,,,说明事件A的发生影响了事件B发生的概率。事件A和事件B相互独立的意义是A是否发生不影响B的概率,并用作为事件A和事件B相互独立的定义。可见,上例中事件A和事件B不相互独立。另一方面,如果事件A和事件B相互独立,概率都大于0,则有. 例2、已知某地区内狗的寿命超过15岁的概率为0.8,超过20岁的概率为0.2.那么该地区内,一只寿命超过15岁的狗,寿命能超过20岁的概率为多少? 解:设A:狗的寿命超过15岁,B:狗的寿命超过20岁,则 注意到,所以 所以 答:该地区内,一只寿命超过15岁的狗,寿命能超过20岁的概率为. 四、探索与研究 条件概率的性质 假设A,B,C都是事件,且.根据条件概率的定义,探索条件概率是否满足下列性质:(1); (2); (3)如果B与C互斥,则 证明:(1)法1: 且互斥 又 法2: 同法1 (2) (3)与互斥, 互斥 (
A
) (
C
) (
B
) 五、小结与巩固 小结:1. 时,已知事件B发生的条件下事件A发生的概率,称为条件概率,记作,且. 2. 求, 法1:在缩小的样本空间上计算事件的概率; 法2:. 3.条件概率满足下列性质: (1); (2); (3)如果B与C互斥,则. 课堂练习: 1.一个袋子里有10个球(除颜色外其他属性都相同),其中4个红球,6个白。甲、乙两人依次不放回地摸取1个球,在甲摸到红球的情况下,乙摸到红球的概率为( ) A. B. C. D. 【答案】A 【详解】在缩小的样本空间上考虑条件概率,甲先摸到1个红球,乙再从剩下的9个球中摸1个球,共有种,其中甲先摸到1个红球,乙再从剩下的3个红球中摸1个球,共有种.所以在甲摸到红球的情况下,乙摸到红球的概率为.故选:A. 2.已知春季里,每天甲、乙两地下雨的概率分别为20%与18%,且两地同时下雨的概率为12%.求春季的一天里: (1)已知甲地下雨的条件下,乙地也下雨的概率; (2)已知乙地下雨的条件下,甲地也下雨的概率. 解:则为 (1) (2) 答:(1)春季的一天里已知甲地下雨的条件下,乙地也下雨的概率为; (2)春季的一天里已知乙地下雨的条件下,甲地也下雨的概率为.
