6.2.1 导数与函数的单调性 教学设计(表格式)
文档属性
| 名称 | 6.2.1 导数与函数的单调性 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 07:32:58 | ||
图片预览

文档简介
教学设计
课程基本信息
课题 §6.2.1导数与函数的单调性
教学目标
1.理解导数与函数单调性的关系; 2.掌握利用导数判断函数单调性的方法,会求一些简单的非初等函数的单调区间; 3.通过对导数与函数单调性关系的学习,体会导数方法在研究函数单调性中的一般性和有效性,同时培养学生直观想象的核心素养。
教学内容
教学重点: 会利用导数判断或证明一些简单的非初等函数的单调性。
教学难点: 如何引导学生建立导数与函数单调性之间的关系。 教学方法: 探究与讲授相结合。
教学过程
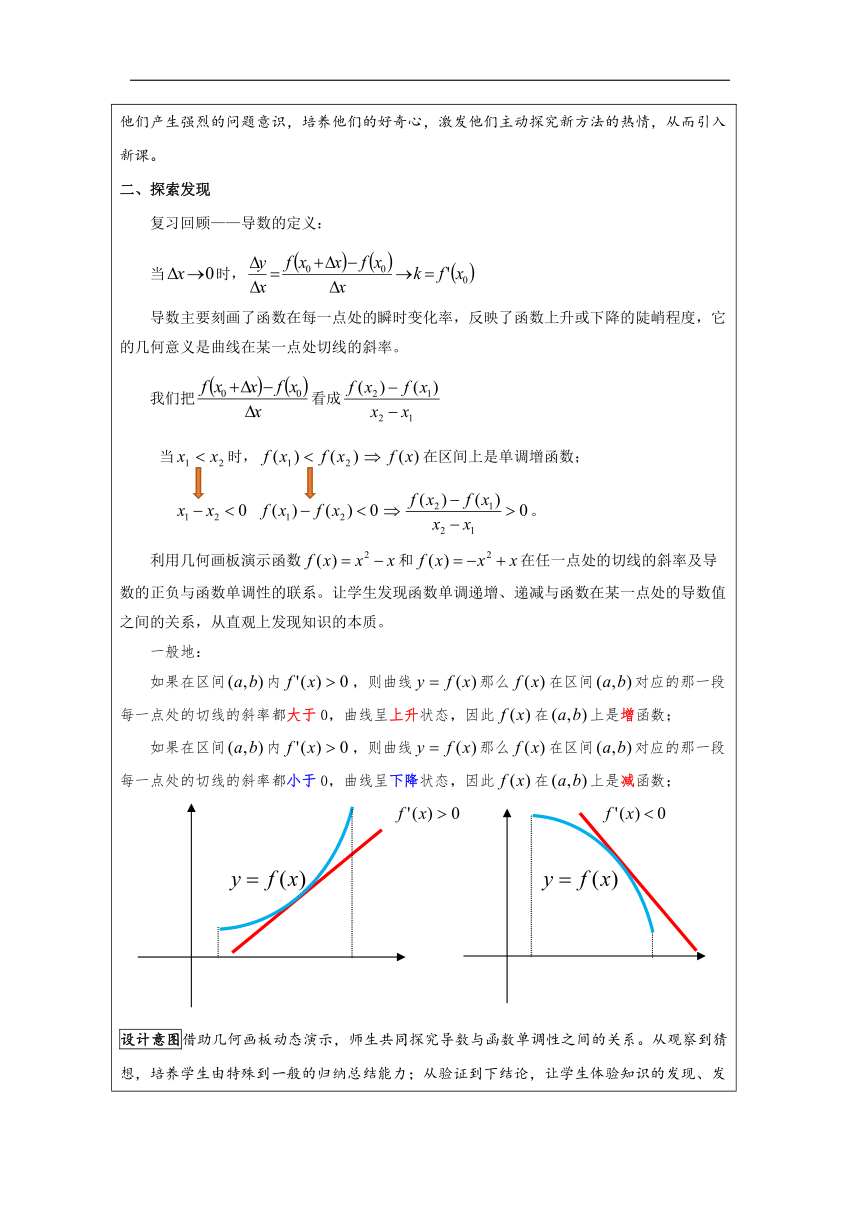
一、问题引入 问题1:判断函数的单调性.(图象法) 问题2:判断函数在上的单调性.(定义法) 复习回顾——函数单调性的定义: 一般地,设函数的定义域为,区间. 如果对任意,当时,都有,则称在上是增函数(也称在上单调递增)。 如果对任意,当时,都有,则称在上是减函数(也称在上单调递减)。 问题3:判断函数的单调性.(图象法?定义法?) 设计意图以问题串的形式复习相关旧知识,同时引出新问题,让学生在操作中遇到困难,使他们产生强烈的问题意识,培养他们的好奇心,激发他们主动探究新方法的热情,从而引入新课。 二、探索发现 复习回顾——导数的定义: 当时, 导数主要刻画了函数在每一点处的瞬时变化率,反映了函数上升或下降的陡峭程度,它的几何意义是曲线在某一点处切线的斜率。 我们把看成 当时,在区间上是单调增函数; 。 利用几何画板演示函数和在任一点处的切线的斜率及导数的正负与函数单调性的联系。让学生发现函数单调递增、递减与函数在某一点处的导数值之间的关系,从直观上发现知识的本质。 一般地: 如果在区间内,则曲线那么在区间对应的那一段每一点处的切线的斜率都大于0,曲线呈上升状态,因此在上是增函数; 如果在区间内,则曲线那么在区间对应的那一段每一点处的切线的斜率都小于0,曲线呈下降状态,因此在上是减函数; 设计意图借助几何画板动态演示,师生共同探究导数与函数单调性之间的关系。从观察到猜想,培养学生由特殊到一般的归纳总结能力;从验证到下结论,让学生体验知识的发现、发生过程。变教师盲目灌输知识为学生主动获取知识,体现学生的主体地位。 三、数学应用 1.回过头来解决问题3(教师板书) 解:的定义域为, 令,解得,所以在上单调递增; 令,解得,所以在上单调递增. 2.再利用导数法解决问题2,并与定义法进行直观对比 3.请同学们自己命制一道题 备选:①求函数的单调区间. ②求函数的单调区间. ③求函数的单调区间. 设计意图 前期由教师规范书写,起到例题的示范作用,同时对比定义法,让学生直观感受到导数法的一般性和有效性;后期设计互动,让学生亲自参与命题,增强学生对知识的理解,同时充分调动学生的积极性。 四、归纳总结 利用导数判断函数单调性的一般步骤(学生作答): ①确定函数的定义域; ②求函数的导数; ③令或,解不等式; ④得到函数的单调增区间或减区间。 设计意图通过实践,学生自主生成利用导数判断函数单调性的一般步骤,随后教师进行完善,并补充说明注意点。这样使知识的生成自然流畅,易于产生深刻的印象。 五、课堂小结 通过这节课的学习,你有哪些收获? 学习了利用导数判断函数单调性的方法以及函数单调区间时的一般步骤;在探究过程中,还体会到数形结合、从特殊到一般等数学思想。 设计意图通过小结,培养学生“学习——总结——反思”的良好习惯,提高学生概括归纳总结的能力。除了知识层面的总结,教师也要强调研究问题方法的渗透。 六、思想升华 问题4:如果函数在某区间上是增函数,那么在该区间上是否必有?(留给学生课后探究) 设计意图留给学生独立思考的时间与空间,让其在课后体会思考的“味道”,使他们重新审视本节课的内容,进一步完善相关结论。 七、板书设计 6.2.1导数与函数的单调性(一) 一、导数与函数单调性的关系 二、利用导数判断函数单调性的一般步骤: 多媒体投影教师板书和学生练习
课程基本信息
课题 §6.2.1导数与函数的单调性
教学目标
1.理解导数与函数单调性的关系; 2.掌握利用导数判断函数单调性的方法,会求一些简单的非初等函数的单调区间; 3.通过对导数与函数单调性关系的学习,体会导数方法在研究函数单调性中的一般性和有效性,同时培养学生直观想象的核心素养。
教学内容
教学重点: 会利用导数判断或证明一些简单的非初等函数的单调性。
教学难点: 如何引导学生建立导数与函数单调性之间的关系。 教学方法: 探究与讲授相结合。
教学过程
一、问题引入 问题1:判断函数的单调性.(图象法) 问题2:判断函数在上的单调性.(定义法) 复习回顾——函数单调性的定义: 一般地,设函数的定义域为,区间. 如果对任意,当时,都有,则称在上是增函数(也称在上单调递增)。 如果对任意,当时,都有,则称在上是减函数(也称在上单调递减)。 问题3:判断函数的单调性.(图象法?定义法?) 设计意图以问题串的形式复习相关旧知识,同时引出新问题,让学生在操作中遇到困难,使他们产生强烈的问题意识,培养他们的好奇心,激发他们主动探究新方法的热情,从而引入新课。 二、探索发现 复习回顾——导数的定义: 当时, 导数主要刻画了函数在每一点处的瞬时变化率,反映了函数上升或下降的陡峭程度,它的几何意义是曲线在某一点处切线的斜率。 我们把看成 当时,在区间上是单调增函数; 。 利用几何画板演示函数和在任一点处的切线的斜率及导数的正负与函数单调性的联系。让学生发现函数单调递增、递减与函数在某一点处的导数值之间的关系,从直观上发现知识的本质。 一般地: 如果在区间内,则曲线那么在区间对应的那一段每一点处的切线的斜率都大于0,曲线呈上升状态,因此在上是增函数; 如果在区间内,则曲线那么在区间对应的那一段每一点处的切线的斜率都小于0,曲线呈下降状态,因此在上是减函数; 设计意图借助几何画板动态演示,师生共同探究导数与函数单调性之间的关系。从观察到猜想,培养学生由特殊到一般的归纳总结能力;从验证到下结论,让学生体验知识的发现、发生过程。变教师盲目灌输知识为学生主动获取知识,体现学生的主体地位。 三、数学应用 1.回过头来解决问题3(教师板书) 解:的定义域为, 令,解得,所以在上单调递增; 令,解得,所以在上单调递增. 2.再利用导数法解决问题2,并与定义法进行直观对比 3.请同学们自己命制一道题 备选:①求函数的单调区间. ②求函数的单调区间. ③求函数的单调区间. 设计意图 前期由教师规范书写,起到例题的示范作用,同时对比定义法,让学生直观感受到导数法的一般性和有效性;后期设计互动,让学生亲自参与命题,增强学生对知识的理解,同时充分调动学生的积极性。 四、归纳总结 利用导数判断函数单调性的一般步骤(学生作答): ①确定函数的定义域; ②求函数的导数; ③令或,解不等式; ④得到函数的单调增区间或减区间。 设计意图通过实践,学生自主生成利用导数判断函数单调性的一般步骤,随后教师进行完善,并补充说明注意点。这样使知识的生成自然流畅,易于产生深刻的印象。 五、课堂小结 通过这节课的学习,你有哪些收获? 学习了利用导数判断函数单调性的方法以及函数单调区间时的一般步骤;在探究过程中,还体会到数形结合、从特殊到一般等数学思想。 设计意图通过小结,培养学生“学习——总结——反思”的良好习惯,提高学生概括归纳总结的能力。除了知识层面的总结,教师也要强调研究问题方法的渗透。 六、思想升华 问题4:如果函数在某区间上是增函数,那么在该区间上是否必有?(留给学生课后探究) 设计意图留给学生独立思考的时间与空间,让其在课后体会思考的“味道”,使他们重新审视本节课的内容,进一步完善相关结论。 七、板书设计 6.2.1导数与函数的单调性(一) 一、导数与函数单调性的关系 二、利用导数判断函数单调性的一般步骤: 多媒体投影教师板书和学生练习
