2.2 等差数列的前n项和公式 课件(共25张PPT)2023-2024学年人教A版(2019)选择性必修第二册
文档属性
| 名称 | 2.2 等差数列的前n项和公式 课件(共25张PPT)2023-2024学年人教A版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 16:57:35 | ||
图片预览








文档简介
(共25张PPT)
等差数列的前n项和公式
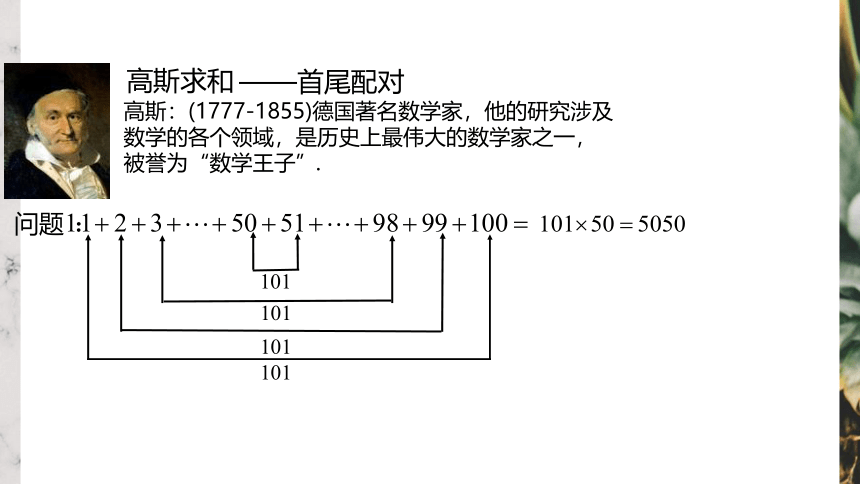
高斯:(1777-1855)德国著名数学家,他的研究涉及数学的各个领域,是历史上最伟大的数学家之一,被誉为“数学王子”.
问题
——首尾配对
高斯求和
问题
设 ,则
那么
其中
等差数列中下标和相等的两项和相等.
思考:你还能想到其他方法吗?
问题 你能用高斯的方法求 吗?
原式
法1
法2
原式
使不同数的求和转化成相同数的求和,
用乘法运算代替加法运算,提高运算效率.
法3
原式
问题 你能用高斯的方法求 吗?
等差数列中下标和相等的两项和相等.
需要对项数的奇偶进行分类讨论.
问题 计算
当 为偶数时,
需要对项数的奇偶进行分类讨论.
问题 计算
当 奇数时,
当 为偶数时,
为偶数,
思考:不分类讨论能否得到最终的结论呢?
问题 计算
对任意正整数 ,都有
思考:这种方法如何巧妙地避免了分类讨论?
倒序求和
第1层1根
第1层1根
第2层2根
第3层3根
第 层 根
第 层 根
第 层 根
第 层 根
因为
所以
问题 倒序求和的方法能否用于求一般的等差数列
的前 项和 ?
①
②
等差数列的性质:若 则
由①+②,
把 代入公式一可得
(公式一)
①
②
把 代入公式一可得
(公式二)
思考:如果不利用公式一的结论,你还有其他方法得到公式二吗?
对任意正整数 ,都有
等差数列 的前 项和公式:
公式一:
功能1:已知 求
练:在等差数列 中, 求
解:
功能2:已知 中任意3个,求第4个.
等差数列 的前 项和公式:
公式一:
等式左右两边同时除以项数 ,得
前 项的平均数
首项 和第 项
的平均数
等差数列 的前 项和公式:
公式二:
功能1:已知 求
功能2:已知 中任意3个,求第4个.
练:在等差数列 中, 求
例:在等差数列 中, 求
解:把 代入公式二,得
整理得
解得 或 (舍去)
又因为 所以
等差数列 的前 项和公式:
公式二:
公式一:
等差数列 的通项公式:
分析:
解:根据公式 ,得
解方程组得
所以
例:已知等差数列 中, ,求
等差数列任意条件
等差数列任意问题
两个相互独立的方程
等差数列任意问题
等差数列任意两个相互独立的条件
基本量法
基本量法
转化与化归
倒序求和
知三求二
方程的思想
课堂小结
等差数列 的前 项和公式:
公式一:
公式二:
等差数列 的通项公式:
课后作业
1.课本22页练习第1题
2.课本24页习题4.2第1题
等差数列的前n项和公式
高斯:(1777-1855)德国著名数学家,他的研究涉及数学的各个领域,是历史上最伟大的数学家之一,被誉为“数学王子”.
问题
——首尾配对
高斯求和
问题
设 ,则
那么
其中
等差数列中下标和相等的两项和相等.
思考:你还能想到其他方法吗?
问题 你能用高斯的方法求 吗?
原式
法1
法2
原式
使不同数的求和转化成相同数的求和,
用乘法运算代替加法运算,提高运算效率.
法3
原式
问题 你能用高斯的方法求 吗?
等差数列中下标和相等的两项和相等.
需要对项数的奇偶进行分类讨论.
问题 计算
当 为偶数时,
需要对项数的奇偶进行分类讨论.
问题 计算
当 奇数时,
当 为偶数时,
为偶数,
思考:不分类讨论能否得到最终的结论呢?
问题 计算
对任意正整数 ,都有
思考:这种方法如何巧妙地避免了分类讨论?
倒序求和
第1层1根
第1层1根
第2层2根
第3层3根
第 层 根
第 层 根
第 层 根
第 层 根
因为
所以
问题 倒序求和的方法能否用于求一般的等差数列
的前 项和 ?
①
②
等差数列的性质:若 则
由①+②,
把 代入公式一可得
(公式一)
①
②
把 代入公式一可得
(公式二)
思考:如果不利用公式一的结论,你还有其他方法得到公式二吗?
对任意正整数 ,都有
等差数列 的前 项和公式:
公式一:
功能1:已知 求
练:在等差数列 中, 求
解:
功能2:已知 中任意3个,求第4个.
等差数列 的前 项和公式:
公式一:
等式左右两边同时除以项数 ,得
前 项的平均数
首项 和第 项
的平均数
等差数列 的前 项和公式:
公式二:
功能1:已知 求
功能2:已知 中任意3个,求第4个.
练:在等差数列 中, 求
例:在等差数列 中, 求
解:把 代入公式二,得
整理得
解得 或 (舍去)
又因为 所以
等差数列 的前 项和公式:
公式二:
公式一:
等差数列 的通项公式:
分析:
解:根据公式 ,得
解方程组得
所以
例:已知等差数列 中, ,求
等差数列任意条件
等差数列任意问题
两个相互独立的方程
等差数列任意问题
等差数列任意两个相互独立的条件
基本量法
基本量法
转化与化归
倒序求和
知三求二
方程的思想
课堂小结
等差数列 的前 项和公式:
公式一:
公式二:
等差数列 的通项公式:
课后作业
1.课本22页练习第1题
2.课本24页习题4.2第1题
