圆的周长 课件(23张PPT)苏教版五年级下册数学
文档属性
| 名称 | 圆的周长 课件(23张PPT)苏教版五年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 09:18:06 | ||
图片预览





文档简介
(共23张PPT)
圆的周长(1)
英寸是英制长度单位。在生活中,人们习惯用英寸作单位来表示自行车车轮的直径。26英寸≈66厘米,24英寸≈61厘米,22英寸≈56厘米。
左边3个自行车车轮各滚动一周,哪个车轮行的路程比较长?
“奥运会自行车比赛”规则:
车轮的直径最大为70厘米,最小55厘米。
61厘米
66厘米
56厘米
同款自行车你会选择哪种车轮参加比赛?
车轮一周的长度是车轮的周长。
正方形的周长是边长的( )倍。
4
正方形的周长=边长×4
边长
PART 02
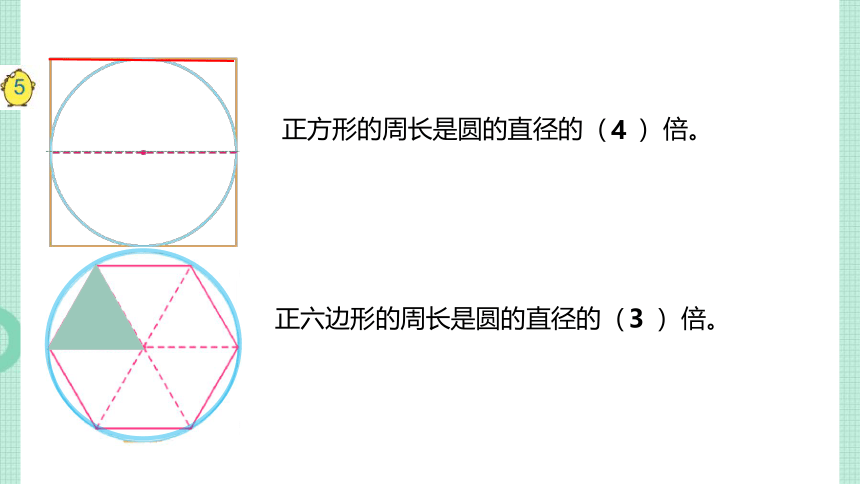
正方形的周长是圆的直径的( )倍。
3
4
正六边形的周长是圆的直径的( )倍。
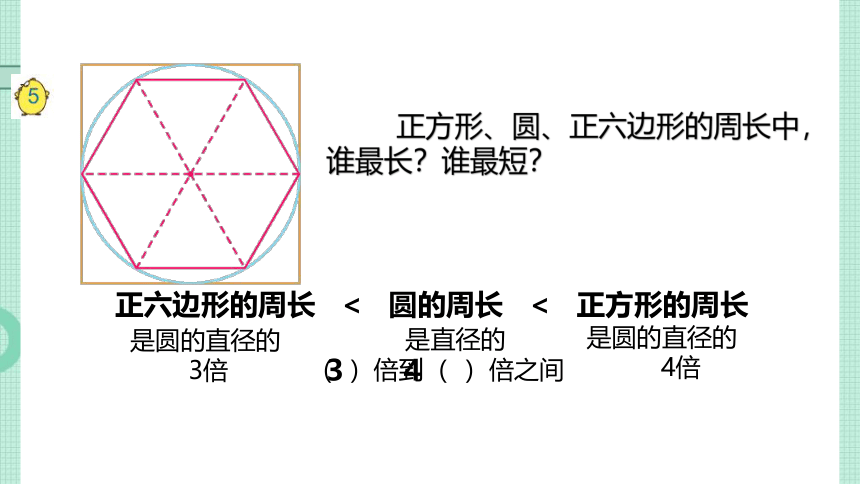
正方形、圆、正六边形的周长中,
谁最长?谁最短?
正六边形的周长 < 圆的周长 < 正方形的周长
3 4
是圆的直径的
3倍
是圆的直径的
4倍
是直径的
( )倍到( )倍之间
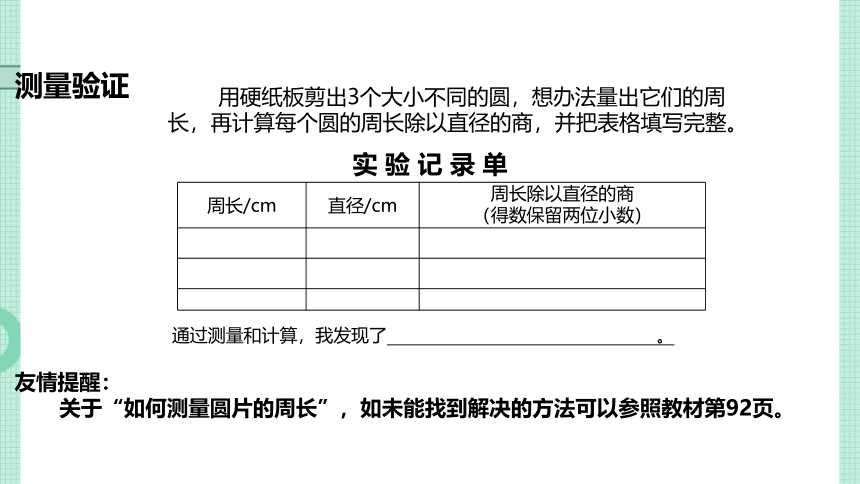
测量验证
友情提醒:
关于“如何测量圆片的周长”,如未能找到解决的方法可以参照教材第92页。
实 验 记 录 单
周长/cm 直径/cm 周长除以直径的商
(得数保留两位小数)
通过测量和计算,我发现了 。
用硬纸板剪出3个大小不同的圆,想办法量出它们的周长,再计算每个圆的周长除以直径的商,并把表格填写完整。
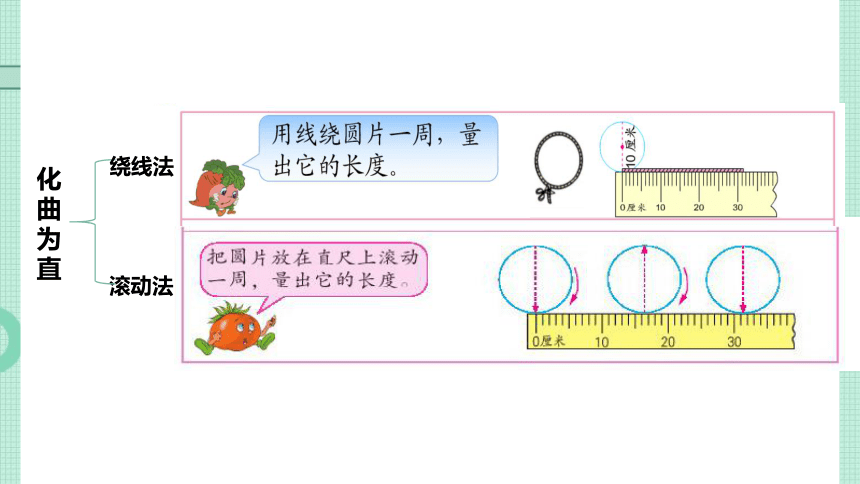
滚动法
化
曲
为
直
绕线法
化曲为直
推理、测量、计算、分析
圆的周长(1)
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
圆的周长(1)
最早的解决方案是测量。人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
日益精确的圆周率
最早的圆周率
古希腊数学家阿基米德发现:
当正多边形的边数增加时,它的形状就越来越接近圆。
阿基米德和圆周率
刘徽的割圆术
我国魏晋时期数学家刘徽采用“割圆术”来求圆的周长的近似值。
他从圆的内接正六边形算起,逐渐把边数加倍,正十二边形,正二十四边形……
求得圆周率的近似值是3.14。
我国南北朝时期的数学家祖冲之使用“缀术”计算圆周率。可惜这种方法早已失传。据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
这一成就,使中国在圆周率的计算方面在世界领先1000年。
最后得出了 的两个分数形式的近似值:约率为 ,
密率为 ,并且精确地算出圆周率在3.1415926和3.1415927之间。
祖冲之算圆周率
电子计算机的出现带来了计算方面的革命, 的小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后12411亿位。
计算机出现以后
π是一个无限不循环小数。
π = 3.141592653…
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
≈3.14
圆的周长 =圆周率×直径
C
=πd
C =2πr
圆的周长(1)
3.14×70=219.8(厘米)
3.14×55=172.7(厘米)
“奥运会自行车比赛”规定:
车轮的直径最大为70厘米,最小55厘米。
这两种车轮周长各是多少厘米?算一算。
1.计算下面各圆的周长。
d=5cm d=3.5dm
r=4cm r=1.2cm
3.14×5=15.7(cm)
3.14×3.5=10.99(dm)
2× 3.14×4=25.12(cm)
2× 3.14×1.2=7.536(cm)
2.摩天轮的半径是10米,坐着它转动一周,大约在空中转过多少米?
2×3.14×10=62.8(米)
答:大约在空中转过62.8 米。
3.小芳骑着车轮直径为70厘米的自行车进行比赛训练,绕着下面运动场骑行一周,是多少米?
3.14×64+100×2
=200.96+200
=400.96(米)
答:是400.96 米。
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
≈3.14
圆的周长 =圆周率×直径
C
=πd
C =2πr
圆的周长(1)
圆的周长(1)
英寸是英制长度单位。在生活中,人们习惯用英寸作单位来表示自行车车轮的直径。26英寸≈66厘米,24英寸≈61厘米,22英寸≈56厘米。
左边3个自行车车轮各滚动一周,哪个车轮行的路程比较长?
“奥运会自行车比赛”规则:
车轮的直径最大为70厘米,最小55厘米。
61厘米
66厘米
56厘米
同款自行车你会选择哪种车轮参加比赛?
车轮一周的长度是车轮的周长。
正方形的周长是边长的( )倍。
4
正方形的周长=边长×4
边长
PART 02
正方形的周长是圆的直径的( )倍。
3
4
正六边形的周长是圆的直径的( )倍。
正方形、圆、正六边形的周长中,
谁最长?谁最短?
正六边形的周长 < 圆的周长 < 正方形的周长
3 4
是圆的直径的
3倍
是圆的直径的
4倍
是直径的
( )倍到( )倍之间
测量验证
友情提醒:
关于“如何测量圆片的周长”,如未能找到解决的方法可以参照教材第92页。
实 验 记 录 单
周长/cm 直径/cm 周长除以直径的商
(得数保留两位小数)
通过测量和计算,我发现了 。
用硬纸板剪出3个大小不同的圆,想办法量出它们的周长,再计算每个圆的周长除以直径的商,并把表格填写完整。
滚动法
化
曲
为
直
绕线法
化曲为直
推理、测量、计算、分析
圆的周长(1)
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
圆的周长(1)
最早的解决方案是测量。人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年前的《周髀算经》。
日益精确的圆周率
最早的圆周率
古希腊数学家阿基米德发现:
当正多边形的边数增加时,它的形状就越来越接近圆。
阿基米德和圆周率
刘徽的割圆术
我国魏晋时期数学家刘徽采用“割圆术”来求圆的周长的近似值。
他从圆的内接正六边形算起,逐渐把边数加倍,正十二边形,正二十四边形……
求得圆周率的近似值是3.14。
我国南北朝时期的数学家祖冲之使用“缀术”计算圆周率。可惜这种方法早已失传。据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
这一成就,使中国在圆周率的计算方面在世界领先1000年。
最后得出了 的两个分数形式的近似值:约率为 ,
密率为 ,并且精确地算出圆周率在3.1415926和3.1415927之间。
祖冲之算圆周率
电子计算机的出现带来了计算方面的革命, 的小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后12411亿位。
计算机出现以后
π是一个无限不循环小数。
π = 3.141592653…
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
≈3.14
圆的周长 =圆周率×直径
C
=πd
C =2πr
圆的周长(1)
3.14×70=219.8(厘米)
3.14×55=172.7(厘米)
“奥运会自行车比赛”规定:
车轮的直径最大为70厘米,最小55厘米。
这两种车轮周长各是多少厘米?算一算。
1.计算下面各圆的周长。
d=5cm d=3.5dm
r=4cm r=1.2cm
3.14×5=15.7(cm)
3.14×3.5=10.99(dm)
2× 3.14×4=25.12(cm)
2× 3.14×1.2=7.536(cm)
2.摩天轮的半径是10米,坐着它转动一周,大约在空中转过多少米?
2×3.14×10=62.8(米)
答:大约在空中转过62.8 米。
3.小芳骑着车轮直径为70厘米的自行车进行比赛训练,绕着下面运动场骑行一周,是多少米?
3.14×64+100×2
=200.96+200
=400.96(米)
答:是400.96 米。
化曲为直
推理、测量、计算、分析
圆的周长÷直径 =
圆周率
π
≈3.14
圆的周长 =圆周率×直径
C
=πd
C =2πr
圆的周长(1)
