2023—2024学年北师大版七年级数学下册4.3探索三角形全等的条件 同步基础解答题专题训练(含答案)
文档属性
| 名称 | 2023—2024学年北师大版七年级数学下册4.3探索三角形全等的条件 同步基础解答题专题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 747.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览



文档简介
2023-2024学年北师大版七年级数学下册《4.3探索三角形全等的条件》
同步基础解答题专题训练(附答案)
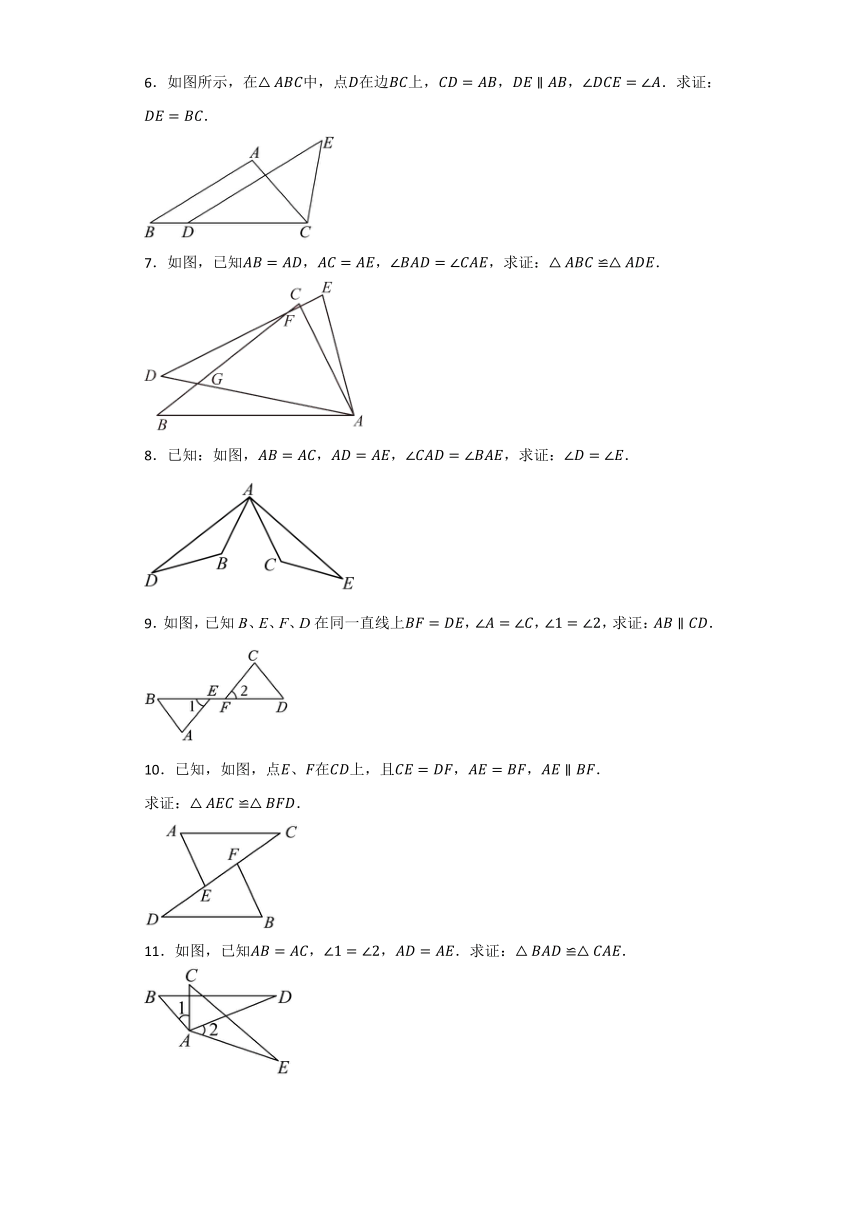
1.如图,,,,垂足分别为D,E.求证:.
2.如图,点D、E在的边上,求证:.
3.如图,C是的中点,,.求证:.
4.如图,在与中,,与全等吗?说明理由.
5.如图所示,点E在上,点D在上,,.求证:.
6.如图所示,在中,点在边上,,,.求证:.
7.如图,已知,,,求证:.
8.已知:如图,,,求证:.
9.如图,已知B、E、F、D在同一直线上,,,求证:.
10.已知,如图,点、在上,且,,.
求证:.
11.如图,已知.求证:.
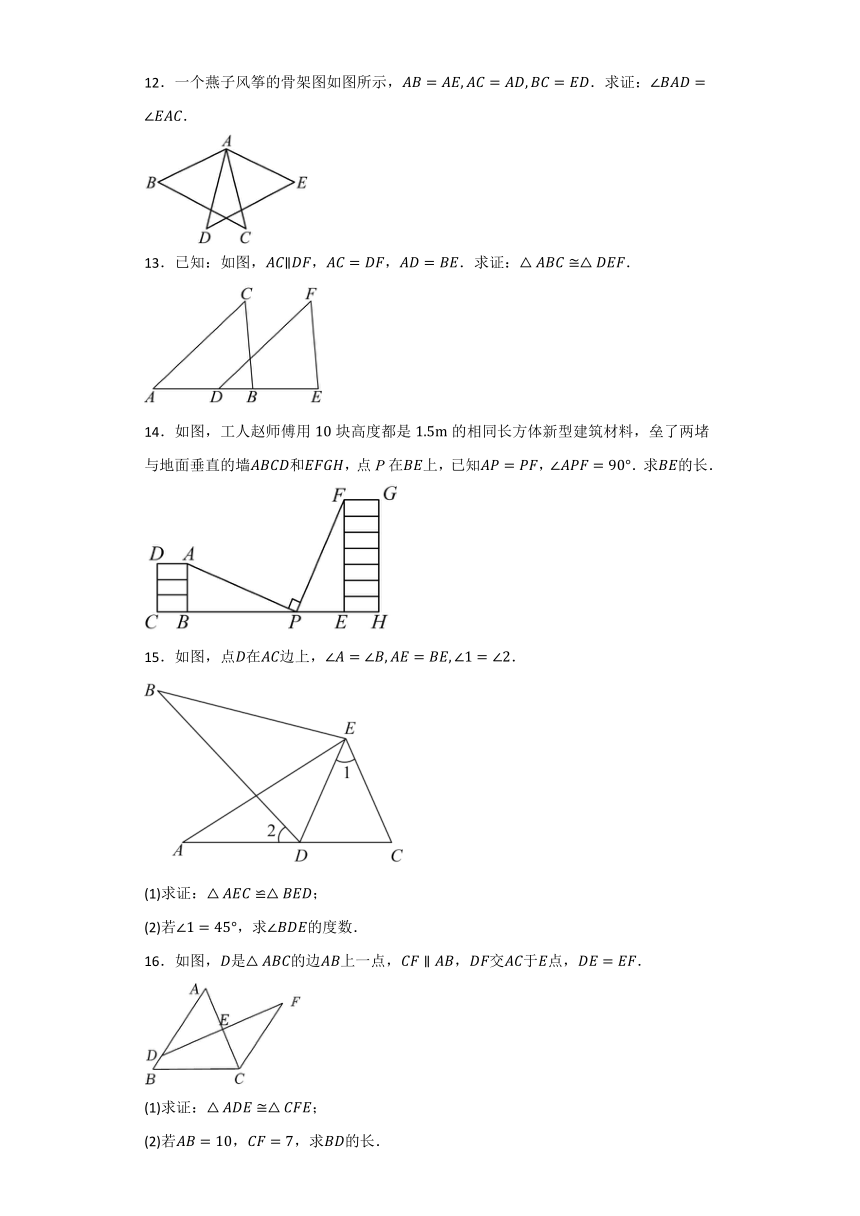
12.一个燕子风筝的骨架图如图所示,.求证:.
13.已知:如图,,,.求证:.
14.如图,工人赵师傅用块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,点P在上,已知,.求的长.
15.如图,点在边上,.
(1)求证:;
(2)若,求的度数.
16.如图,是的边上一点,,交于点,.
(1)求证:;
(2)若,,求的长.
17.如图,在中,是边上的中线,于点E,交的延长线于点F.
(1)求证:;
(2)若=16,求的长.
18.如图,点在同一条直线上,点分别在直线的两侧,且.
(1)求证:;
(2)若,求的长.
19.(1)如图1,和相交于点,,,求证:;
(2)如图2,,,,求证:.
20.如图,工人师傅要检查人字梁的和是否相等,但他手边没有量角器,只有一个刻度尺. 他是这样操作的:
①分别在和上取;
②在上取;
③连接,量出的长等于的长,则能说明和是相等的,他的这种做法合理吗?为什么?
参考答案
1.证明:∵,,
∴,
又∵,
∴,
∴.
2.证明:∵,
∴
∵,
∴
∴,
∴
3.证明:∵C是的中点,
∴
在和中,
,
∴.
4.解:与全等,理由如下:
在和中,
,
∴.
5.证明:在和中,
,
∴.
6.证明:,
.
在和中,
.
7.证明:,
,即,
在和中
,
.
8.证明:∵,
∴,即,
在和中
,
∴.
∴.
9.解:∵,
∴,
∴,
在和中,
,
∴,
∴,
∴.
10.证明:,
,
在和中,
.
11.证明:∵,
∴,即,
在和中,
,
∴.
12.证明:在与中,
,,,
,
,
,
.
13.证明:,
,
.
,
,
又,
.
14.解:∵,,
∴,
∴.
在与中,
∵,,,
∴ ,
∴ , ,
∴ .
15.(1)证明:∵,
∴
∵
∴()
(2)解:∵
∴
∴,
∵
∴
∴
16.(1)证明:,
,,
在和中,
,
;
(2)由(1)可知,,
,
,
,
即的长是3.
17.(1)证明:是的边上的中线,
,
,
.
在和中,
,
,
.
(2)由(1)知,
,
,
,
,
∴.
故.
18.(1)证明:,,且,
,
在和中,
,
.
(2)解:,
,
,
,
的长为5.
19.解:(1)在和中,
∴
(2)∵,
∴,
即:,
在和中,
∴
∴
∴
20.解:这种做法合理.
理由:在和中,
∵,,.
∴.
∴.
同步基础解答题专题训练(附答案)
1.如图,,,,垂足分别为D,E.求证:.
2.如图,点D、E在的边上,求证:.
3.如图,C是的中点,,.求证:.
4.如图,在与中,,与全等吗?说明理由.
5.如图所示,点E在上,点D在上,,.求证:.
6.如图所示,在中,点在边上,,,.求证:.
7.如图,已知,,,求证:.
8.已知:如图,,,求证:.
9.如图,已知B、E、F、D在同一直线上,,,求证:.
10.已知,如图,点、在上,且,,.
求证:.
11.如图,已知.求证:.
12.一个燕子风筝的骨架图如图所示,.求证:.
13.已知:如图,,,.求证:.
14.如图,工人赵师傅用块高度都是的相同长方体新型建筑材料,垒了两堵与地面垂直的墙和,点P在上,已知,.求的长.
15.如图,点在边上,.
(1)求证:;
(2)若,求的度数.
16.如图,是的边上一点,,交于点,.
(1)求证:;
(2)若,,求的长.
17.如图,在中,是边上的中线,于点E,交的延长线于点F.
(1)求证:;
(2)若=16,求的长.
18.如图,点在同一条直线上,点分别在直线的两侧,且.
(1)求证:;
(2)若,求的长.
19.(1)如图1,和相交于点,,,求证:;
(2)如图2,,,,求证:.
20.如图,工人师傅要检查人字梁的和是否相等,但他手边没有量角器,只有一个刻度尺. 他是这样操作的:
①分别在和上取;
②在上取;
③连接,量出的长等于的长,则能说明和是相等的,他的这种做法合理吗?为什么?
参考答案
1.证明:∵,,
∴,
又∵,
∴,
∴.
2.证明:∵,
∴
∵,
∴
∴,
∴
3.证明:∵C是的中点,
∴
在和中,
,
∴.
4.解:与全等,理由如下:
在和中,
,
∴.
5.证明:在和中,
,
∴.
6.证明:,
.
在和中,
.
7.证明:,
,即,
在和中
,
.
8.证明:∵,
∴,即,
在和中
,
∴.
∴.
9.解:∵,
∴,
∴,
在和中,
,
∴,
∴,
∴.
10.证明:,
,
在和中,
.
11.证明:∵,
∴,即,
在和中,
,
∴.
12.证明:在与中,
,,,
,
,
,
.
13.证明:,
,
.
,
,
又,
.
14.解:∵,,
∴,
∴.
在与中,
∵,,,
∴ ,
∴ , ,
∴ .
15.(1)证明:∵,
∴
∵
∴()
(2)解:∵
∴
∴,
∵
∴
∴
16.(1)证明:,
,,
在和中,
,
;
(2)由(1)可知,,
,
,
,
即的长是3.
17.(1)证明:是的边上的中线,
,
,
.
在和中,
,
,
.
(2)由(1)知,
,
,
,
,
∴.
故.
18.(1)证明:,,且,
,
在和中,
,
.
(2)解:,
,
,
,
的长为5.
19.解:(1)在和中,
∴
(2)∵,
∴,
即:,
在和中,
∴
∴
∴
20.解:这种做法合理.
理由:在和中,
∵,,.
∴.
∴.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
