第18章《平行四边形》单元测试(含答案)
文档属性
| 名称 | 第18章《平行四边形》单元测试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
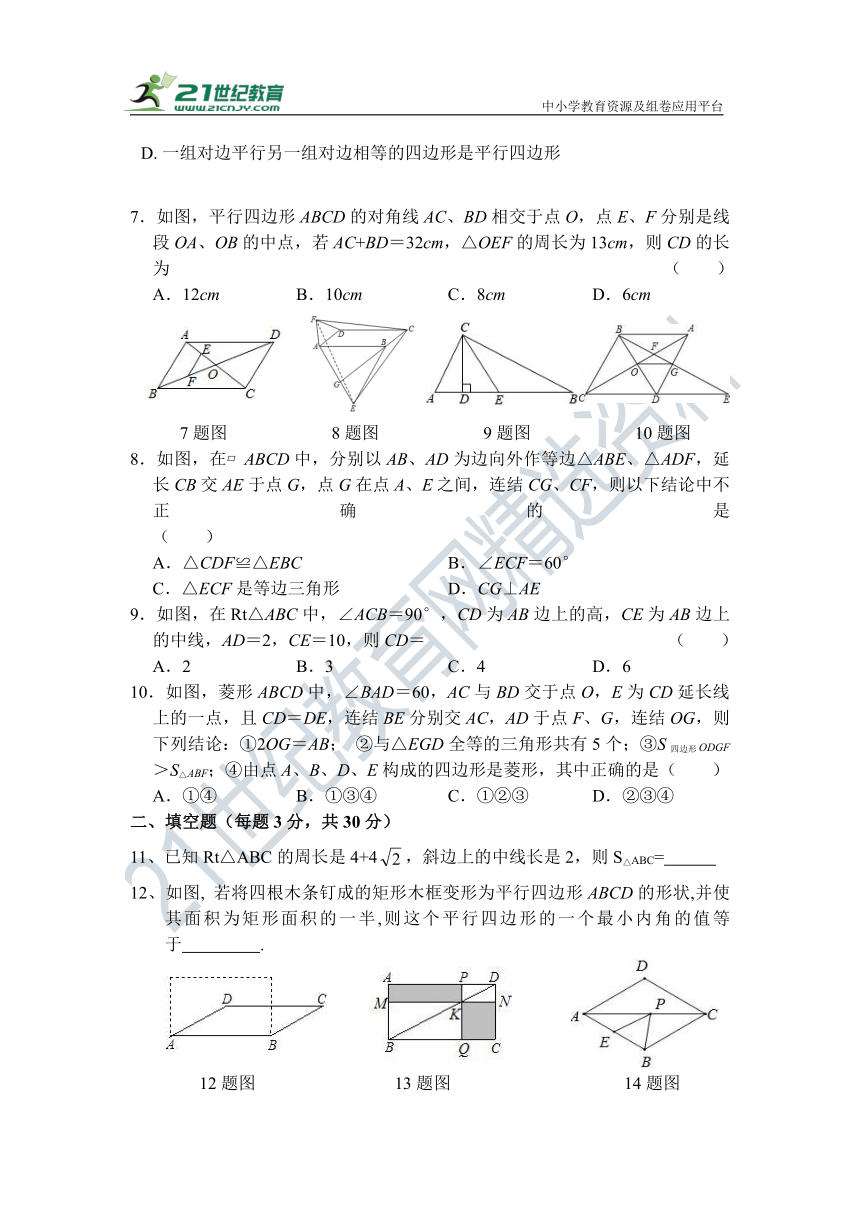
1.在平行四边形ABCD中,若∠A=60°,则∠B的度数是 ( )
A.30° B.60° C.90° D.120°
2.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,若∠BAD=70°,则∠CFD等于 ( )
A.50° B.60° C.70° D.80°
2题图 3题图 4题图
3.如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为 ( )
A. B.2 C.2 D.4
4.如图,在△ABC中,点D、E分别是边AB、AC的中点,已知DE=6cm,则BC的长是 ( )
A. 3cm B. 12cm C. 18cm D. 9cm
5.如图,E ,F分别是□ABCD的两对边的中点,则图中平行四边形的个数是( )
A. 3 B. 4 C. 5 D. 6
6.下列说法中,不正确是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对角分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边平行另一组对边相等的四边形是平行四边形
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为 ( )
A.12cm B.10cm C.8cm D.6cm
7题图 8题图 9题图 10题图
8.如图,在 ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是 ( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
9.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD= ( )
A.2 B.3 C.4 D.6
10.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB; ②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形,其中正确的是( )
A.①④ B.①③④ C.①②③ D.②③④
二、填空题(每题3分,共30分)
11、已知Rt△ABC的周长是4+4,斜边上的中线长是2,则S△ABC=
12、如图, 若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于 .
12题图 13题图 14题图
13、如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1 S2(填“>”或“<”或“=”).
14. 如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
15,如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
15题图 17题图 18题图
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17.如图,在△ABC中,AB=AC=12,BC=8,BE是高,且点D、F分别是边AB、BC的中点,则△DEF的周长等于 .
18.如图,在四边形ABCD中,AD∥BC,AD=5,BC=18,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,当运动时间t秒时,以点P,Q,E,D为顶点的四边形是平行四边形,则t的值为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD.
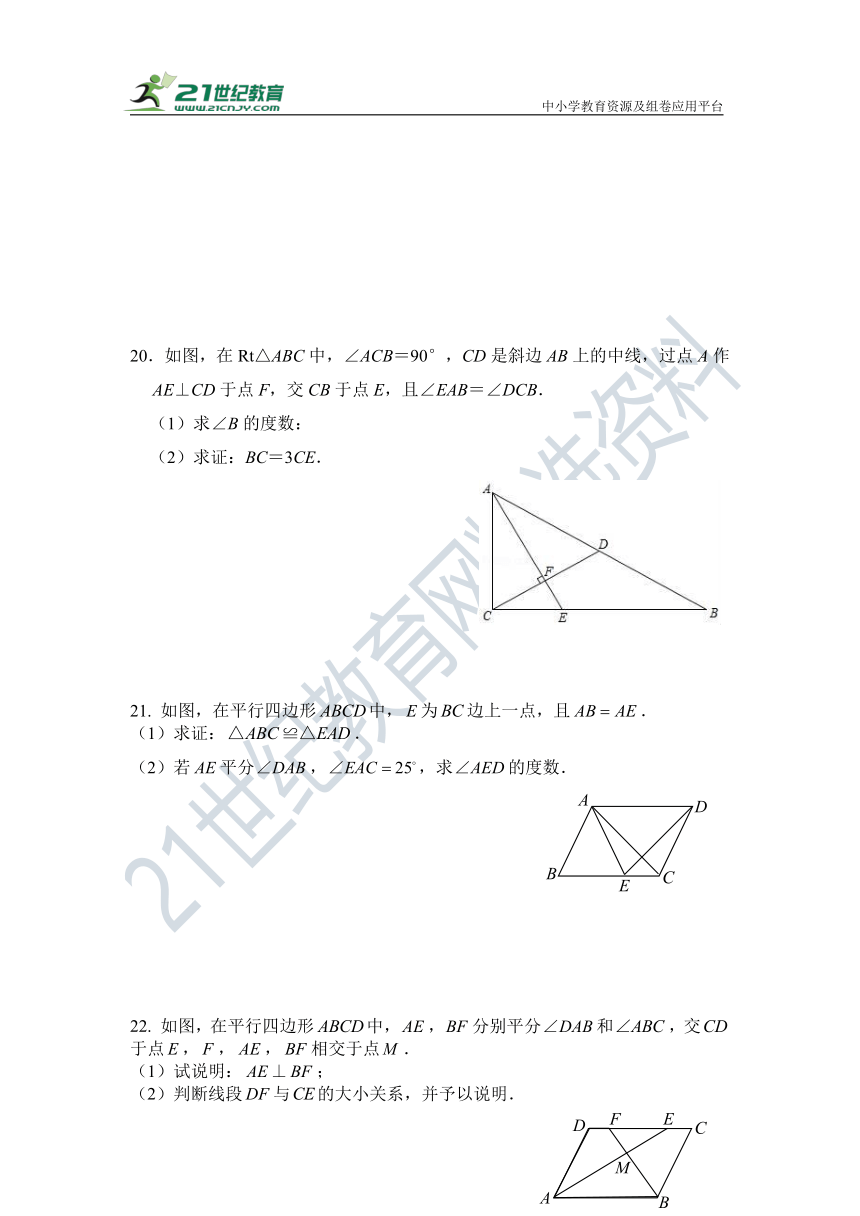
20.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
21. 如图,在平行四边形中,为边上一点,且.
(1)求证:.
(2)若平分,,求的度数.
22. 如图,在平行四边形中,,分别平分和,交于点,,,相交于点.
(1)试说明:;
(2)判断线段与的大小关系,并予以说明.
23.如图,在长方形ABCD中,AB=10,AD=4,E为边CD上一点,CE=7,点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为ts.
(1)当t=1时,判断△PAE是否为直角三角形,说明理由;
(2)是否存在这样的t,使EA平分∠PED?若存在,求出t的值;若不存在,请说明理由.
24.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B B D D D D A
二、填空题(每题3分,共24分)
11、4 12、30° 13、S1 = S2
14.4﹣2或3.
14.
15. 67.5.
16. 9;
17.【分析】由三角形中位线定理和直角三角形斜边上的中线性质求出DF、EF、DE的长,即可得出答案.
【解答】解:∵点D、F分别是边AB、BC的中点,AB=AC=12,BE是高,
∴DF是△ABC的中位线,AF⊥BC,BE⊥AC,
∴DF=AC=6,EF=BC=4,DE=AB=6,
∴△DEF的周长=DF+EF+DE=6+4+6=16;
故答案为:16.
【点评】此题考查的直角三角形斜边上的中线性质、等腰三角形的性质、三角形中位线的性质,熟记以上性质是解题的关键.
18.【分析】由AD∥BC,则PD=QE时,以点P,Q,E,D为顶点的四边形是平行四边形,
①当Q运动到E和C之间时,设运动时间为t,则得:9﹣3t=5﹣t,解方程即可,
②当Q运动到E和B之间时,设运动时间为t,则得:3t﹣9=5﹣t,解方程即可.
【解答】解:∵E是BC的中点,
∴BE=CE=BC=9,
∵AD∥BC,
∴PD=QE时,以点P,Q,E,D为顶点的四边形是平行四边形,
①当Q运动到E和C之间时,设运动时间为t,
则得:9﹣3t=5﹣t,
解得:t=2,
②当Q运动到E和B之间时,设运动时间为t,
则得:3t﹣9=5﹣t,
解得:t=3.5;
∴当运动时间t为2秒或3.5秒时,以点P,Q,E,D为顶点的四边形是平行四边形,
故答案为:2秒或3.5秒.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.【分析】首先根据等腰三角形的性质可得F是AD中点,再根据三角形的中位线定理可得EF=BD.
【解答】证明:∵CD=CA,CF平分∠ACB,
∴F是AD中点,
∵AE=EB,
∴E是AB中点,∴EF是△ABD的中位线,
∴EF=BD.
【点评】此题主要考查了三角形中位线定理,以及等腰三角形的性质,关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
20.【分析】(1)根据余角的性质得到∠ECF=∠CAF,求得∠CAD=2∠DCB,由CD是斜边AB上的中线,得到CD=BD,推出∠CAB=2∠B,于是得到结论;
(2)根据直角三角形的性质即可得到结论.
【解答】解:(1)∵AE⊥CD,
∴∠AFC=∠ACB=90°,
∴∠CAF+∠ACF=∠ACF+∠ECF=90°,
∴∠ECF=∠CAF,
∵∠EAD=∠DCB,
∴∠CAD=2∠DCB,
∵CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠DCB,
∴∠CAB=2∠B,
∵∠B+∠CAB=90°,
∴∠B=30°;
(2)∵∠B=∠BAE=∠CAE=30°,
∴AE=BE,CE=AE,
∴BC=3CE.
21.(1)四边形为平行四边形,
.
.
.
.
.
(2),
.
为等边三角形.
.
.
,
.
22.解:(1)方法一:如图①
在ABCD中,
,分别平分和
,
即
.
方法二:如图②,延长,相交于点
在ABCD中,
平分
平分
即.
(2)方法一:线段与是相等关系,即
在ABCD中,
又平分
同理可得,
又在ABCD中,
即.
方法二:如右图,延长,相交于点,延长,相交于点
在ABCD中,
平分
同理可得,
在ABCD中,
又在中,
,
,
.
23.【解答】解:(1)过点P作PF⊥CD于点F,如图:
由题意得BP=t,AP=10﹣t,PF=4,EF=7﹣t.
当t=1时,△PAE不是直角三角形,理由如下:
当t=1时,
PE2=PF2+EF2=42+(7﹣t)2=16+36=52,AP2=(10﹣t)2=81,
∵在长方形ABCD中,AB=10,CE=7,
∴DC=AB=10,
∴DE=DC﹣CE=10﹣7=3,
又AD=4,
∴AE2=32+42=25,
∵81≠52+25,
∴AP2≠PE2+EA2,
∴△PAE不是直角三角形;
(2)存在这样的t,使EA平分∠PED,理由如下:
若EA平分∠PED,则∠AED=∠PEA,
∵四边形ABCD为长方形,
∴CD∥AB,
∴∠AED=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA=10﹣t,
∵PF⊥CD,
∴∠PFD=90°,
又∵在长方形ABCD中,∠D=∠DAB=90°,
∴四边形PADF为长方形,
∴PF=AD=4,
在Rt△PEF中,EP2=EF2+PF2,
∴(10﹣t)2=42+(7﹣t)2,
解得:t=.
24.【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB=,
∴AH2=BH2==3,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG=+1.
5题图
图①
图②
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在平行四边形ABCD中,若∠A=60°,则∠B的度数是 ( )
A.30° B.60° C.90° D.120°
2.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,若∠BAD=70°,则∠CFD等于 ( )
A.50° B.60° C.70° D.80°
2题图 3题图 4题图
3.如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为 ( )
A. B.2 C.2 D.4
4.如图,在△ABC中,点D、E分别是边AB、AC的中点,已知DE=6cm,则BC的长是 ( )
A. 3cm B. 12cm C. 18cm D. 9cm
5.如图,E ,F分别是□ABCD的两对边的中点,则图中平行四边形的个数是( )
A. 3 B. 4 C. 5 D. 6
6.下列说法中,不正确是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对角分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边平行另一组对边相等的四边形是平行四边形
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为 ( )
A.12cm B.10cm C.8cm D.6cm
7题图 8题图 9题图 10题图
8.如图,在 ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是 ( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
9.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD= ( )
A.2 B.3 C.4 D.6
10.如图,菱形ABCD中,∠BAD=60,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE分别交AC,AD于点F、G,连结OG,则下列结论:①2OG=AB; ②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形,其中正确的是( )
A.①④ B.①③④ C.①②③ D.②③④
二、填空题(每题3分,共30分)
11、已知Rt△ABC的周长是4+4,斜边上的中线长是2,则S△ABC=
12、如图, 若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于 .
12题图 13题图 14题图
13、如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1 S2(填“>”或“<”或“=”).
14. 如图:菱形ABCD中,AB=2,∠B=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
15,如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=________度.
15题图 17题图 18题图
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17.如图,在△ABC中,AB=AC=12,BC=8,BE是高,且点D、F分别是边AB、BC的中点,则△DEF的周长等于 .
18.如图,在四边形ABCD中,AD∥BC,AD=5,BC=18,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,当运动时间t秒时,以点P,Q,E,D为顶点的四边形是平行四边形,则t的值为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF=BD.
20.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
21. 如图,在平行四边形中,为边上一点,且.
(1)求证:.
(2)若平分,,求的度数.
22. 如图,在平行四边形中,,分别平分和,交于点,,,相交于点.
(1)试说明:;
(2)判断线段与的大小关系,并予以说明.
23.如图,在长方形ABCD中,AB=10,AD=4,E为边CD上一点,CE=7,点P从点B出发,以每秒1个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为ts.
(1)当t=1时,判断△PAE是否为直角三角形,说明理由;
(2)是否存在这样的t,使EA平分∠PED?若存在,求出t的值;若不存在,请说明理由.
24.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B B D D D D A
二、填空题(每题3分,共24分)
11、4 12、30° 13、S1 = S2
14.4﹣2或3.
14.
15. 67.5.
16. 9;
17.【分析】由三角形中位线定理和直角三角形斜边上的中线性质求出DF、EF、DE的长,即可得出答案.
【解答】解:∵点D、F分别是边AB、BC的中点,AB=AC=12,BE是高,
∴DF是△ABC的中位线,AF⊥BC,BE⊥AC,
∴DF=AC=6,EF=BC=4,DE=AB=6,
∴△DEF的周长=DF+EF+DE=6+4+6=16;
故答案为:16.
【点评】此题考查的直角三角形斜边上的中线性质、等腰三角形的性质、三角形中位线的性质,熟记以上性质是解题的关键.
18.【分析】由AD∥BC,则PD=QE时,以点P,Q,E,D为顶点的四边形是平行四边形,
①当Q运动到E和C之间时,设运动时间为t,则得:9﹣3t=5﹣t,解方程即可,
②当Q运动到E和B之间时,设运动时间为t,则得:3t﹣9=5﹣t,解方程即可.
【解答】解:∵E是BC的中点,
∴BE=CE=BC=9,
∵AD∥BC,
∴PD=QE时,以点P,Q,E,D为顶点的四边形是平行四边形,
①当Q运动到E和C之间时,设运动时间为t,
则得:9﹣3t=5﹣t,
解得:t=2,
②当Q运动到E和B之间时,设运动时间为t,
则得:3t﹣9=5﹣t,
解得:t=3.5;
∴当运动时间t为2秒或3.5秒时,以点P,Q,E,D为顶点的四边形是平行四边形,
故答案为:2秒或3.5秒.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.【分析】首先根据等腰三角形的性质可得F是AD中点,再根据三角形的中位线定理可得EF=BD.
【解答】证明:∵CD=CA,CF平分∠ACB,
∴F是AD中点,
∵AE=EB,
∴E是AB中点,∴EF是△ABD的中位线,
∴EF=BD.
【点评】此题主要考查了三角形中位线定理,以及等腰三角形的性质,关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
20.【分析】(1)根据余角的性质得到∠ECF=∠CAF,求得∠CAD=2∠DCB,由CD是斜边AB上的中线,得到CD=BD,推出∠CAB=2∠B,于是得到结论;
(2)根据直角三角形的性质即可得到结论.
【解答】解:(1)∵AE⊥CD,
∴∠AFC=∠ACB=90°,
∴∠CAF+∠ACF=∠ACF+∠ECF=90°,
∴∠ECF=∠CAF,
∵∠EAD=∠DCB,
∴∠CAD=2∠DCB,
∵CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠DCB,
∴∠CAB=2∠B,
∵∠B+∠CAB=90°,
∴∠B=30°;
(2)∵∠B=∠BAE=∠CAE=30°,
∴AE=BE,CE=AE,
∴BC=3CE.
21.(1)四边形为平行四边形,
.
.
.
.
.
(2),
.
为等边三角形.
.
.
,
.
22.解:(1)方法一:如图①
在ABCD中,
,分别平分和
,
即
.
方法二:如图②,延长,相交于点
在ABCD中,
平分
平分
即.
(2)方法一:线段与是相等关系,即
在ABCD中,
又平分
同理可得,
又在ABCD中,
即.
方法二:如右图,延长,相交于点,延长,相交于点
在ABCD中,
平分
同理可得,
在ABCD中,
又在中,
,
,
.
23.【解答】解:(1)过点P作PF⊥CD于点F,如图:
由题意得BP=t,AP=10﹣t,PF=4,EF=7﹣t.
当t=1时,△PAE不是直角三角形,理由如下:
当t=1时,
PE2=PF2+EF2=42+(7﹣t)2=16+36=52,AP2=(10﹣t)2=81,
∵在长方形ABCD中,AB=10,CE=7,
∴DC=AB=10,
∴DE=DC﹣CE=10﹣7=3,
又AD=4,
∴AE2=32+42=25,
∵81≠52+25,
∴AP2≠PE2+EA2,
∴△PAE不是直角三角形;
(2)存在这样的t,使EA平分∠PED,理由如下:
若EA平分∠PED,则∠AED=∠PEA,
∵四边形ABCD为长方形,
∴CD∥AB,
∴∠AED=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA=10﹣t,
∵PF⊥CD,
∴∠PFD=90°,
又∵在长方形ABCD中,∠D=∠DAB=90°,
∴四边形PADF为长方形,
∴PF=AD=4,
在Rt△PEF中,EP2=EF2+PF2,
∴(10﹣t)2=42+(7﹣t)2,
解得:t=.
24.【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB=,
∴AH2=BH2==3,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG=+1.
5题图
图①
图②
