北师大版初中数学七年级下册期中测试卷(困难)(含解析)
文档属性
| 名称 | 北师大版初中数学七年级下册期中测试卷(困难)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 476.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版初中数学七年级下册期中测试卷
考试范围:一二三章;考试时间:120分钟;分数:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列计算正确的是( )
A. B.
C. D.
2.某桑蚕丝的直径约为米,将用科学记数法表示是( )
A. B. C. D.
3.如图,下列说法不正确的是( )
A. 与是同位角
B. 与是同位角
C. 与是内错角
D. 与是同旁内角
4.如图,点在直线上,平分,,那么下列说法不一定正确的是
.( )
A. 与互补 B. 与互余
C. 与互余 D. 与相等
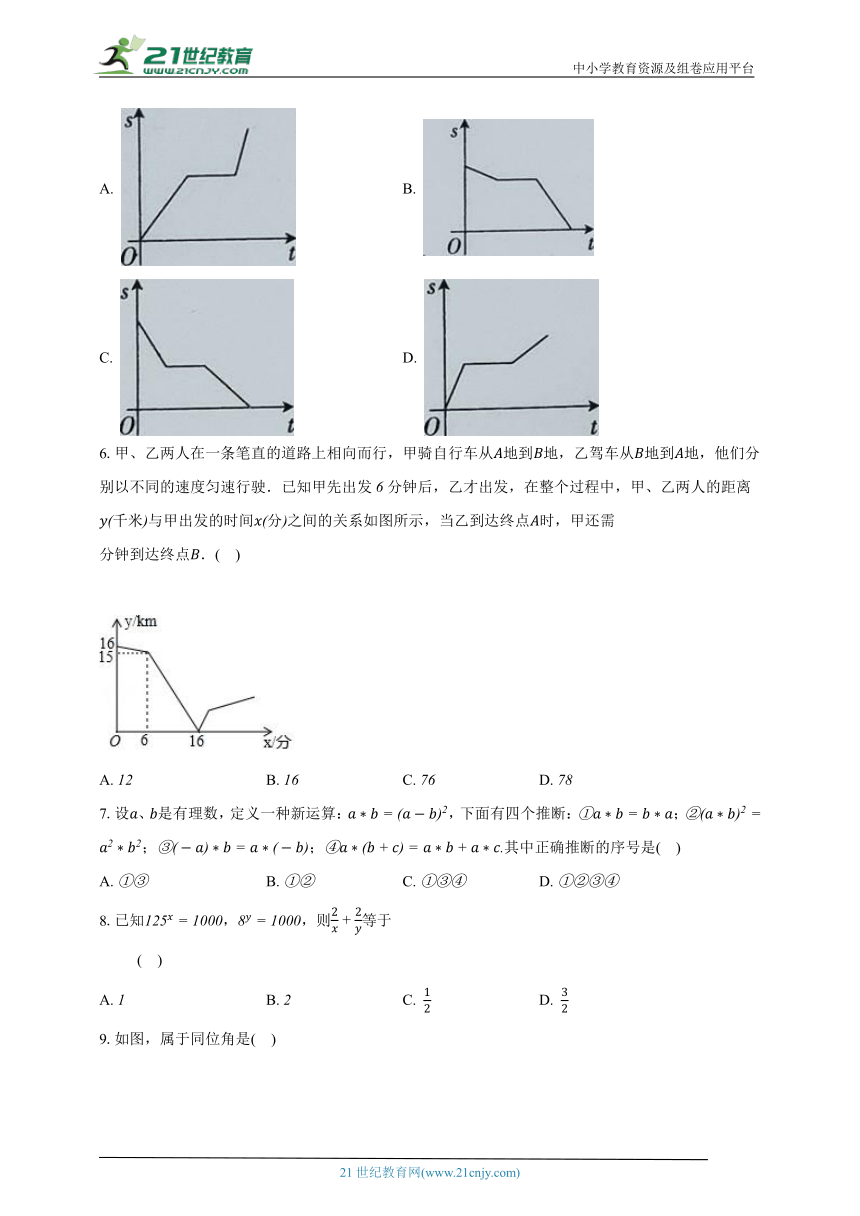
5.明明在爬山的活动中,先快速跑步上山,累了停下来休息了一段时间后,再慢慢爬到山顶,下图中能大致反映明明离山顶的路程与登山时间的关系的是( )
A. B.
C. D.
6.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从地到地,乙驾车从地到地,他们分别以不同的速度匀速行驶.已知甲先出发分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,当乙到达终点时,甲还需
分钟到达终点.( )
A. B. C. D.
7.设、是有理数,定义一种新运算:,下面有四个推断:;;;其中正确推断的序号是( )
A. B. C. D.
8.已知,,则等于
( )
A. B. C. D.
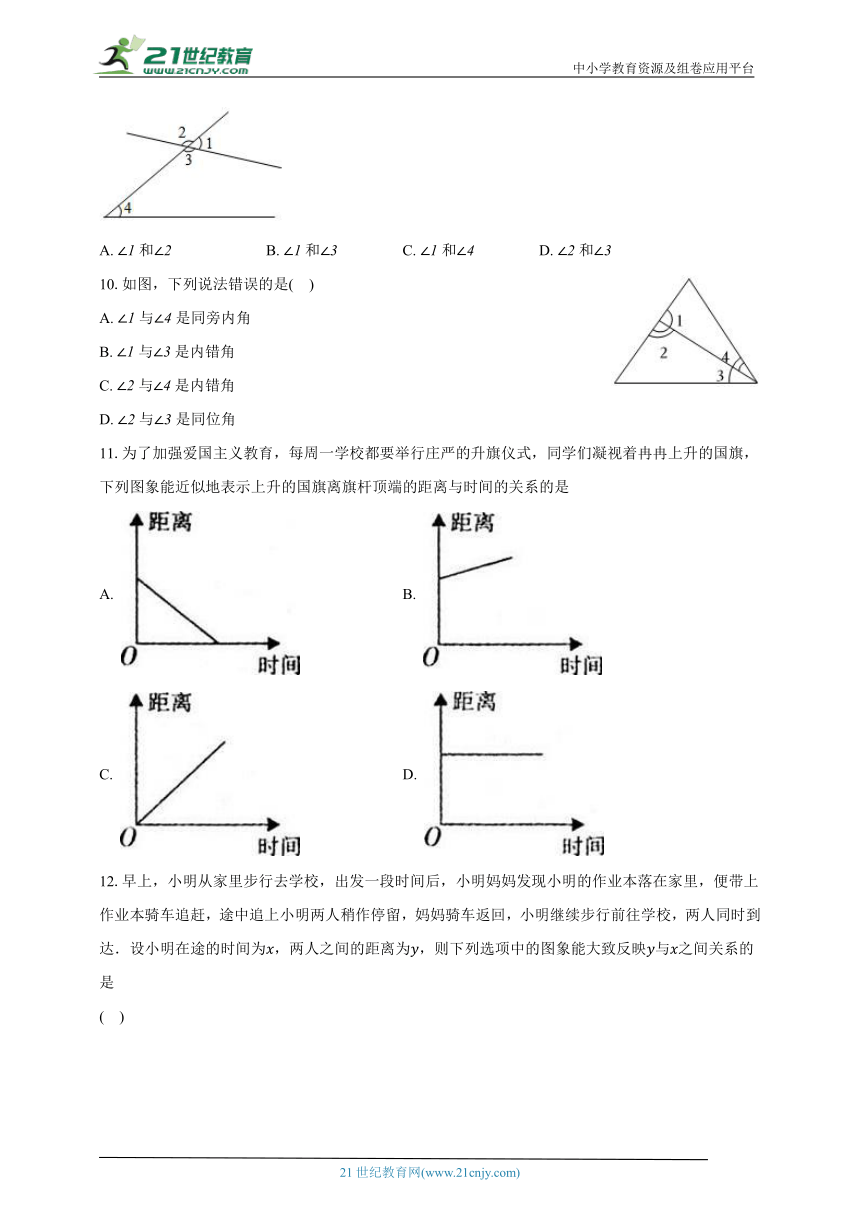
9.如图,属于同位角是( )
A. 和 B. 和 C. 和 D. 和
10.如图,下列说法错误的是( )
A. 与是同旁内角
B. 与是内错角
C. 与是内错角
D. 与是同位角
11.为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列图象能近似地表示上升的国旗离旗杆顶端的距离与时间的关系的是
A. B.
C. D.
12.早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为,两人之间的距离为,则下列选项中的图象能大致反映与之间关系的是
( )
A. B.
C. D.
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
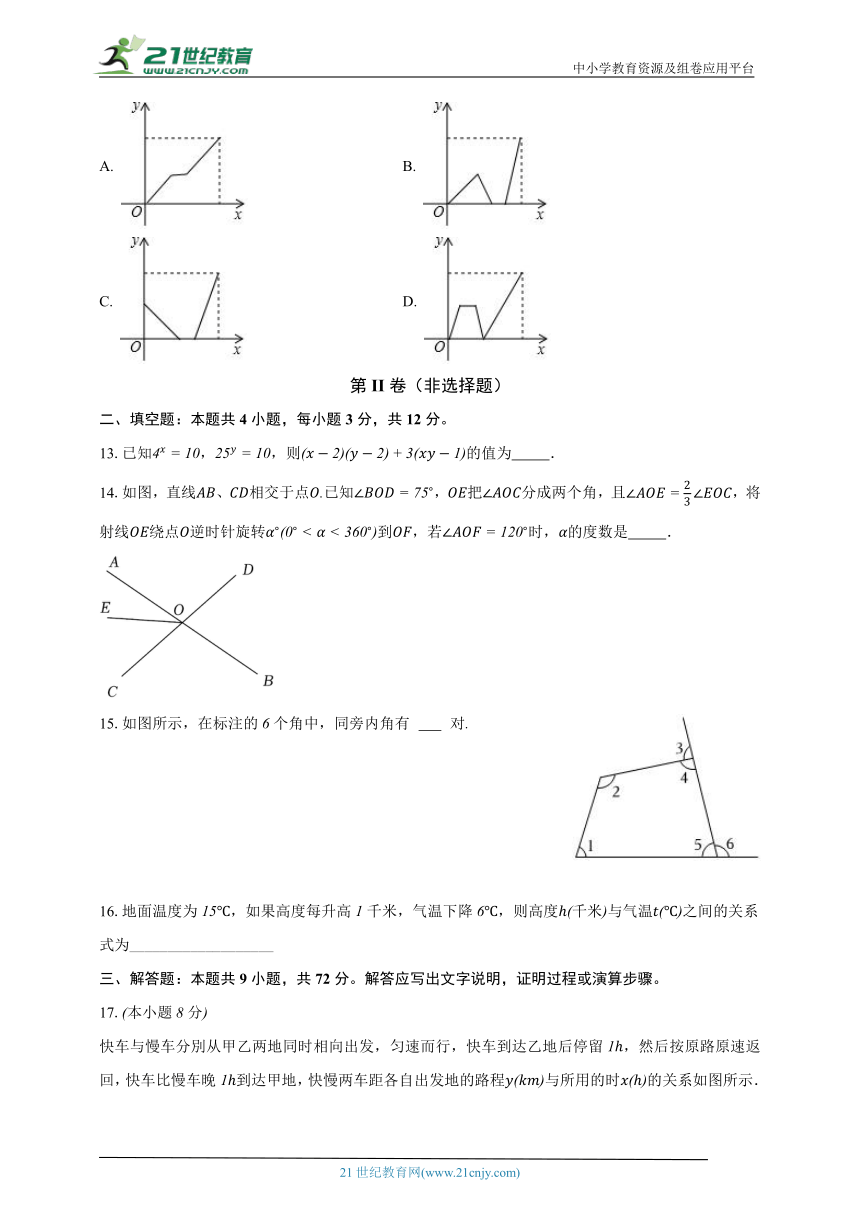
13.已知,,则的值为 .
14.如图,直线、相交于点已知,把分成两个角,且,将射线绕点逆时针旋转到,若时,的度数是 .
15.如图所示,在标注的个角中,同旁内角有 对
16.地面温度为,如果高度每升高千米,气温下降,则高度千米与气温之间的关系式为___________________
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
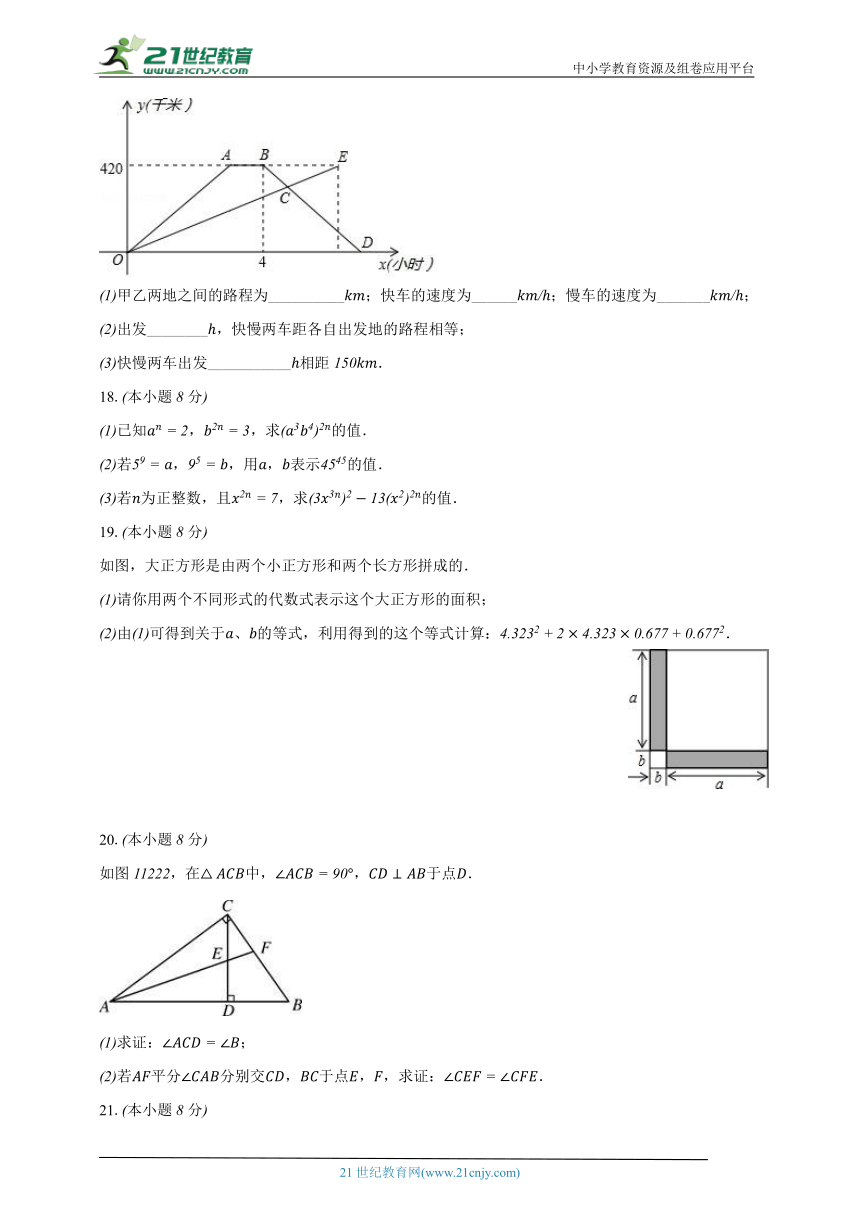
快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留,然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时的关系如图所示.
甲乙两地之间的路程为__________;快车的速度为______;慢车的速度为_______;
出发________,快慢两车距各自出发地的路程相等;
快慢两车出发___________相距.
18.本小题分
已知,,求的值.
若,,用,表示的值.
若为正整数,且,求的值.
19.本小题分
如图,大正方形是由两个小正方形和两个长方形拼成的.
请你用两个不同形式的代数式表示这个大正方形的面积;
由可得到关于、的等式,利用得到的这个等式计算:.
20.本小题分
如图,在中,,于点.
求证:;
若平分分别交,于点,,求证:.
21.本小题分
如图,是直线上一点,为任一条射线,平分,平分.
图中的邻补角为______,的邻补角为______;
如果,那么______,如果,那么______;
试猜想与具有怎样的数量关系,并说明理由.
22.本小题分
如图,直线、交于点,,是的平分线,是的平分线,.
求的度数;
求的度数.
23.本小题分
A、两地相距,甲于某日骑自行车从地出发驶往地,乙也于同日下午骑摩托车从地出发驶往地,在这个变化过程中,甲和乙所行驶的路程用变量表示,甲所用的时间用变量时表示,图中折线和线段分别表示甲和乙所行驶的路程与时间的变化关系,请根据图象回答:
直接写出:甲出发后______小时,乙才开始出发;
请分别求出甲出发小时后的速度和乙的行驶速度?
求乙行驶几小时后追上甲,此时两人距地还有多少千米?
24.本小题分
小明同学骑自行车去郊游,如图所示表示他离家的距离千米与所用时间时之间关系的图象.
根据图象回答,小明到达离家最远的地方需几小时?此时离家多远?
求小明出发小时时离家多远?
求小明出发多长时间离家千米?
25.本小题分
图是由边长分别为,的两个正方形拼成的图形,其面积为,图是长、宽分别为,的长方形,其面积为.
图是由图中的图形补成的大正方形,其面积为,则,,的数量关系是______;
对于图,通过两种不同方法计算它的面积,可以得到一个代数恒等式是:_______;
在图边长为的正方形中放入两个边长为的小正方形,得到图所示的图形,若,,求图中阴影部分的面积.
答案和解析
1.【答案】
【解析】解:和不能合并,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:.
根据完全平方公式,幂的乘方与积的乘方,合并同类项法则进行计算,再得出选项即可.
本题考查了完全平方公式,幂的乘方与积的乘方,合并同类项法则等知识点,能熟记掌握完全平方公式、幂的乘方与积的乘方、合并同类项法则是解此题的关键.
2.【答案】
【解析】解:;
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
3.【答案】
【解析】解:、和是同位角,说法正确,故选项不符合题意;
B、和是同位角,说法正确,故选项不符合题意;
C、和是内错角,说法正确,故选项不符合题意;
D、和不是同旁内角,说法错误,故选项符合题意.
故选:.
根据同位角、内错角和同旁内角的定义判断即可,同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线截线的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
本题主要考查了“三线八角”,同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形是解题的关键.
4.【答案】
【解析】【分析】根据角平分线定义,可得 ;由,可得,从而得到由平角的定义及角的和差关系可得,通过等量代换可得,根据,不一定等于,逐一判断,即可得到答案.本题考查了角分线的定义,同等角的余补角相等的知识点,解题的关键是结合图形进行分析.
【详解】解:平分,.
又,,.
故、正确,不符合题意.
,
,
故正确,不符合题意.
,不一定等于,
不一定等于,
故A 不一定正确,符合题意,
故选: .
5.【答案】
【解析】【分析】
根据题意可以判断哪个选项中的函数图象符合题意,从而可以解答本题.本题考查函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【解答】
解:由题意可得, 刚开始,小明跑步上山,随着的增加而减小,变化趋势比较快,
休息一段时间,这个过程,随着的增加不变, 慢慢走完剩下的路程,随着的增加而减小,变化趋势比较缓慢,
故选C.
6.【答案】
【解析】【分析】
本题考查了用图象表示变量之间的关系的有关知识,根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达站需要的时间,再根据有理数的减法,可得答案.
【解答】
解:由纵坐标看出甲先行驶了千米,由横坐标看出甲行驶千米用了分钟,
甲的速度是千米分钟,
由纵坐标看出两地的距离是千米,
设乙的速度是千米分钟,由题意,得
,
解得千米分钟,
相遇后乙到达站还需分钟
相遇后甲到达站还需分钟,
当乙到达终点时,甲还需分钟到达终点,
故选D.
7.【答案】
【解析】解:根据题中的新定义得:
,,易知故正确;
,,,故不正确;
, ,故正确;
,,,故不正确.
综上,正确的推断有.
故选:.
本题考查了完全平方公式,新定义问题,弄清题中的新定义以及乘法公式是解本题的关键.
根据题中的新定义进行计算,逐项判断即可.
8.【答案】
【解析】【分析】
本题考查幂的乘方与积的乘方、同底数幂相乘法则,考查学生灵活运用公式的能力.
由题意可知:,,然后利用,从而求出答案.
【解答】
解:由题意可知:,,
,
,
,
,
故选:.
9.【答案】
【解析】解:由同位角的定义可知,和是同位角,
故选:.
根据两条直线被第三条直线所截,位于这两条直线的同侧和截线的同旁,这样的两个角为同位角进行判断即可.
本题考查同位角的定义,理解同位角的意义是正确判断的前提.
10.【答案】
【解析】解:、与是同旁内角,正确,故此选项不符合题意;
B、与是内错角,正确,故此选项不符合题意;
C、与是内错角,正确,故此选项不符合题意;
D、与不是同旁内角,原说法不正确,故此选项符合题意;
故选:.
根据同位角、内错角、同旁内角的意义,可得答案.
本题考查了同位角、内错角、同旁内角,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
11.【答案】
【解析】【分析】
本题考查了函数的图象,一次函数的性质,根据题意得出国旗离旗杆顶端的距离与时间的函数关系式是解题的关键.设旗杆高,国旗上升的速度为,根据国旗离旗杆顶端的距离旗杆的高度国旗上升的距离,得出,再利用一次函数的性质即可求解.
【解答】
解:设旗杆高,国旗上升的速度为,国旗离旗杆顶端的距离为,
根据题意,得,
、是常数,
是的一次函数,
,,
随的增大而减小.
故选A.
12.【答案】
【解析】【分析】
本题考查了函数图象,动点函数的图象的有关知识,读懂题意,把整个过程分解成分段图象是解题的关键.根据题意,把图象分为四段,第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,第二段妈妈骑车追赶到追上小明,第三段两人稍作停留,第四段妈妈骑车返回,小明继续步行前往学校,两人同时到达.分析图象,然后选择答案.
【解答】
解:根据题意可得,与的函数关系的大致图象分为四段,
第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,两人的距离在慢慢增大,
第二段,妈妈骑车追赶到追上小明,两人的距离在减小,
第三段,两人稍作停留,两人的距离为,
第四段,妈妈骑车返回,小明继续步行前往学校,两人同时到达,两人的距离在快速增大,
纵观各选项,只有选项的图象符合.
故选B.
13.【答案】
【解析】【分析】
本题考查了幂的乘方和积的乘方的逆运算,掌握幂的乘方和积的乘方的法则是解决问题的关键.
【解答】
解:,,
,,
,
,
,
,
.
故答案为.
14.【答案】或
【解析】在运动过程中由两个位置可以使,分别作出对应的图象,根据的度数以及与间的比例求出两角的值,进而可求出角的度数.
【解答】解:当运动到如图所示的位置时,
,
,
,
,
当时,
,
如图所示,当运动到如图所示的位置时,
,
,
,
,
当时,
,
故答案为:或.
15.【答案】
【解析】解:和是同旁内角,
和是同旁内角,
和是同旁内角,
和是同旁内角,
故在标注的个角中,同旁内角有对.
故答案为:.
根据同旁内角的定义判断即可,两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
本题考查了同旁内角的定义,解题的关键是掌握同旁内角的定义,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
16.【答案】
【解析】【分析】
升高千米就可求得温度的下降值,进而求得千米处的温度.
正确理解高度每升高千米,气温下降,的含义是解题关键.
【解答】
解:高度千米与气温之间的关系式为:.
故答案为.
17.【答案】;;;
;
或或.
【解析】【分析】
本题考查了用图像表示变量之间的关系,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于表示出快车距离出发地的路程.
先得两地的距离,根据速度路程时间列式计算即可求出快车和慢车的速度;
根据两车的速度等条件可得出答案;
分别根据两车相遇前、两车相遇后以及快车从乙往甲返回途中,三种情况两车距离为时,列方程可解答.
【解答】
解:由图可知:甲乙两地之间的路程为;
快车的速度为:;
由题意得:快车小时到达甲地,则慢车小时到达甲地,
则慢车的速度为:;
故答案为:,,;
设经过小时后,快、慢两车距各自出发地的路程相等,
则
解得:,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
第一种情形第一次没有相遇前,相距,
则,
解得:,
第二种情形应是相遇后而快车没到乙地前,
解得:,
第三种情形是快车从乙往甲返回途中:,
解得:,
综上所述:快慢两车出发或或相距.
故答案为:或或.
18.【答案】解:原式
.
因为,,
所以.
原式
.
因为,
所以原式.
【解析】本题考查幂的乘方与积的乘方以及整体代入法.
先运用积的乘方法则进行计算,然后转化为已知条件,再把已知条件代入即可;
易得,,将转化为,再把已知条件代入即可解答;
先把转化为,再把已知条件代入即可解答.
19.【答案】解:大正方形的面积为:,
四部分的面积的和为:;
等式为:,
分
【解析】根据正方形的面积公式利用大正方形的边长解答,两个阴影部分长方形的面积加上两个正方形的面积进行表示;
根据大正方形的面积相等可得关于、的等式,利用等式代入数据进行计算即可求解.
本题考查了完全平方公式的几何背景,根据同一个图形的面积的不同表示方法得到等式是解题的关键.
20.【答案】证明:,于,
,,
;
在中,,
同理在中,.
又平分,
,
,
又,
.
【解析】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.
由于与都是的余角,根据同角的余角相等即可得证;
根据直角三角形两锐角互余得出,,再根据角平分线的定义得出,然后由对顶角相等的性质,等量代换即可证明.
21.【答案】,;
,;
由题意可得:
.
【解析】解:如图所示:
的邻补角为,
的邻补角为,
故答案为:,;
,,
,
,
,
,
,
,
故答案为:,;
见答案.
22.【答案】解:,
,
;
又是的平分线,
,
,
,
又是的平分线,
,
,
.
【解析】根据垂线的定义,由,得,推断出;
根据角平分线的定义,由是的平分线,得,是的平分线,得,进而解答问题.
本题考查了角平分线定义和角的有关计算.解题的关键是掌握角平分线定义和角的有关计算的方法.
23.【答案】解:;
乙的速度为:千米时,
甲出发小时后的速度为:千米时
设乙行驶小时后追上甲,
根据题意得
解得,
即乙行驶小时后追上甲,此时两人距地还有千米;
答:乙行驶小时后追上甲,此时两人距地还有千米.
【解析】本题考查了变量之间的图象:如果把自变量与因变量的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是变量之间关系图象.
观察图象得到甲出发后小时,乙才开始出发;
根据图象得到乙用小时走了千米,甲前小时走了千米,后面小时走了千米,然后利用速度公式计算他们的速度;
设乙行驶小时后追上甲,利用他们所走路程相等列方程,然后解方程求出,再利用千米减去他们已经走的路程得到两人距地的距离.
24.【答案】解:由图象可知小明到达离家最远的地方需小时;
此时他离家千米;
设直线的解析式为,由、,
代入得:,
解得:,
故直线的解析式为:,
当时,.
答:出发两个半小时,小明离家千米;
设过、两点的直线解析式为,
由、,代入得
,
解得:,
故直线的解析式为:,
过、两点的直线解析式为,
,
分别令,则,,
解得:,,
答:小明出发小时或小时距家千米.
【解析】根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需小时;此时,他离家千米;
因为、在直线上,运用待定系数法求出解析式后,把代入解析式即可;
分别利用待定系数法求得过、两点的直线解析式,以及、两点的直线解析式.分别令,求解.
此题主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.
25.【答案】【小问详解】
由题意知:,.
,
,
,
,
故答案为:;
【小问详解】
,
,
,
,
故答案为:;
【小问详解】
,,,
,,
,
又,
,
,
.
【解析】【分析】因为整体图形的面积等于各部分面积之和,所以,故;
;
因为,所以,由,,,可得;
此题主要考查整式的混合运算,熟练掌握整式的混合运算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版初中数学七年级下册期中测试卷
考试范围:一二三章;考试时间:120分钟;分数:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列计算正确的是( )
A. B.
C. D.
2.某桑蚕丝的直径约为米,将用科学记数法表示是( )
A. B. C. D.
3.如图,下列说法不正确的是( )
A. 与是同位角
B. 与是同位角
C. 与是内错角
D. 与是同旁内角
4.如图,点在直线上,平分,,那么下列说法不一定正确的是
.( )
A. 与互补 B. 与互余
C. 与互余 D. 与相等
5.明明在爬山的活动中,先快速跑步上山,累了停下来休息了一段时间后,再慢慢爬到山顶,下图中能大致反映明明离山顶的路程与登山时间的关系的是( )
A. B.
C. D.
6.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从地到地,乙驾车从地到地,他们分别以不同的速度匀速行驶.已知甲先出发分钟后,乙才出发,在整个过程中,甲、乙两人的距离千米与甲出发的时间分之间的关系如图所示,当乙到达终点时,甲还需
分钟到达终点.( )
A. B. C. D.
7.设、是有理数,定义一种新运算:,下面有四个推断:;;;其中正确推断的序号是( )
A. B. C. D.
8.已知,,则等于
( )
A. B. C. D.
9.如图,属于同位角是( )
A. 和 B. 和 C. 和 D. 和
10.如图,下列说法错误的是( )
A. 与是同旁内角
B. 与是内错角
C. 与是内错角
D. 与是同位角
11.为了加强爱国主义教育,每周一学校都要举行庄严的升旗仪式,同学们凝视着冉冉上升的国旗,下列图象能近似地表示上升的国旗离旗杆顶端的距离与时间的关系的是
A. B.
C. D.
12.早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为,两人之间的距离为,则下列选项中的图象能大致反映与之间关系的是
( )
A. B.
C. D.
第II卷(非选择题)
二、填空题:本题共4小题,每小题3分,共12分。
13.已知,,则的值为 .
14.如图,直线、相交于点已知,把分成两个角,且,将射线绕点逆时针旋转到,若时,的度数是 .
15.如图所示,在标注的个角中,同旁内角有 对
16.地面温度为,如果高度每升高千米,气温下降,则高度千米与气温之间的关系式为___________________
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留,然后按原路原速返回,快车比慢车晚到达甲地,快慢两车距各自出发地的路程与所用的时的关系如图所示.
甲乙两地之间的路程为__________;快车的速度为______;慢车的速度为_______;
出发________,快慢两车距各自出发地的路程相等;
快慢两车出发___________相距.
18.本小题分
已知,,求的值.
若,,用,表示的值.
若为正整数,且,求的值.
19.本小题分
如图,大正方形是由两个小正方形和两个长方形拼成的.
请你用两个不同形式的代数式表示这个大正方形的面积;
由可得到关于、的等式,利用得到的这个等式计算:.
20.本小题分
如图,在中,,于点.
求证:;
若平分分别交,于点,,求证:.
21.本小题分
如图,是直线上一点,为任一条射线,平分,平分.
图中的邻补角为______,的邻补角为______;
如果,那么______,如果,那么______;
试猜想与具有怎样的数量关系,并说明理由.
22.本小题分
如图,直线、交于点,,是的平分线,是的平分线,.
求的度数;
求的度数.
23.本小题分
A、两地相距,甲于某日骑自行车从地出发驶往地,乙也于同日下午骑摩托车从地出发驶往地,在这个变化过程中,甲和乙所行驶的路程用变量表示,甲所用的时间用变量时表示,图中折线和线段分别表示甲和乙所行驶的路程与时间的变化关系,请根据图象回答:
直接写出:甲出发后______小时,乙才开始出发;
请分别求出甲出发小时后的速度和乙的行驶速度?
求乙行驶几小时后追上甲,此时两人距地还有多少千米?
24.本小题分
小明同学骑自行车去郊游,如图所示表示他离家的距离千米与所用时间时之间关系的图象.
根据图象回答,小明到达离家最远的地方需几小时?此时离家多远?
求小明出发小时时离家多远?
求小明出发多长时间离家千米?
25.本小题分
图是由边长分别为,的两个正方形拼成的图形,其面积为,图是长、宽分别为,的长方形,其面积为.
图是由图中的图形补成的大正方形,其面积为,则,,的数量关系是______;
对于图,通过两种不同方法计算它的面积,可以得到一个代数恒等式是:_______;
在图边长为的正方形中放入两个边长为的小正方形,得到图所示的图形,若,,求图中阴影部分的面积.
答案和解析
1.【答案】
【解析】解:和不能合并,故本选项不符合题意;
B.,故本选项不符合题意;
C.,故本选项符合题意;
D.,故本选项不符合题意;
故选:.
根据完全平方公式,幂的乘方与积的乘方,合并同类项法则进行计算,再得出选项即可.
本题考查了完全平方公式,幂的乘方与积的乘方,合并同类项法则等知识点,能熟记掌握完全平方公式、幂的乘方与积的乘方、合并同类项法则是解此题的关键.
2.【答案】
【解析】解:;
故选:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
3.【答案】
【解析】解:、和是同位角,说法正确,故选项不符合题意;
B、和是同位角,说法正确,故选项不符合题意;
C、和是内错角,说法正确,故选项不符合题意;
D、和不是同旁内角,说法错误,故选项符合题意.
故选:.
根据同位角、内错角和同旁内角的定义判断即可,同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线截线的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
本题主要考查了“三线八角”,同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形是解题的关键.
4.【答案】
【解析】【分析】根据角平分线定义,可得 ;由,可得,从而得到由平角的定义及角的和差关系可得,通过等量代换可得,根据,不一定等于,逐一判断,即可得到答案.本题考查了角分线的定义,同等角的余补角相等的知识点,解题的关键是结合图形进行分析.
【详解】解:平分,.
又,,.
故、正确,不符合题意.
,
,
故正确,不符合题意.
,不一定等于,
不一定等于,
故A 不一定正确,符合题意,
故选: .
5.【答案】
【解析】【分析】
根据题意可以判断哪个选项中的函数图象符合题意,从而可以解答本题.本题考查函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【解答】
解:由题意可得, 刚开始,小明跑步上山,随着的增加而减小,变化趋势比较快,
休息一段时间,这个过程,随着的增加不变, 慢慢走完剩下的路程,随着的增加而减小,变化趋势比较缓慢,
故选C.
6.【答案】
【解析】【分析】
本题考查了用图象表示变量之间的关系的有关知识,根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达站需要的时间,再根据有理数的减法,可得答案.
【解答】
解:由纵坐标看出甲先行驶了千米,由横坐标看出甲行驶千米用了分钟,
甲的速度是千米分钟,
由纵坐标看出两地的距离是千米,
设乙的速度是千米分钟,由题意,得
,
解得千米分钟,
相遇后乙到达站还需分钟
相遇后甲到达站还需分钟,
当乙到达终点时,甲还需分钟到达终点,
故选D.
7.【答案】
【解析】解:根据题中的新定义得:
,,易知故正确;
,,,故不正确;
, ,故正确;
,,,故不正确.
综上,正确的推断有.
故选:.
本题考查了完全平方公式,新定义问题,弄清题中的新定义以及乘法公式是解本题的关键.
根据题中的新定义进行计算,逐项判断即可.
8.【答案】
【解析】【分析】
本题考查幂的乘方与积的乘方、同底数幂相乘法则,考查学生灵活运用公式的能力.
由题意可知:,,然后利用,从而求出答案.
【解答】
解:由题意可知:,,
,
,
,
,
故选:.
9.【答案】
【解析】解:由同位角的定义可知,和是同位角,
故选:.
根据两条直线被第三条直线所截,位于这两条直线的同侧和截线的同旁,这样的两个角为同位角进行判断即可.
本题考查同位角的定义,理解同位角的意义是正确判断的前提.
10.【答案】
【解析】解:、与是同旁内角,正确,故此选项不符合题意;
B、与是内错角,正确,故此选项不符合题意;
C、与是内错角,正确,故此选项不符合题意;
D、与不是同旁内角,原说法不正确,故此选项符合题意;
故选:.
根据同位角、内错角、同旁内角的意义,可得答案.
本题考查了同位角、内错角、同旁内角,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
11.【答案】
【解析】【分析】
本题考查了函数的图象,一次函数的性质,根据题意得出国旗离旗杆顶端的距离与时间的函数关系式是解题的关键.设旗杆高,国旗上升的速度为,根据国旗离旗杆顶端的距离旗杆的高度国旗上升的距离,得出,再利用一次函数的性质即可求解.
【解答】
解:设旗杆高,国旗上升的速度为,国旗离旗杆顶端的距离为,
根据题意,得,
、是常数,
是的一次函数,
,,
随的增大而减小.
故选A.
12.【答案】
【解析】【分析】
本题考查了函数图象,动点函数的图象的有关知识,读懂题意,把整个过程分解成分段图象是解题的关键.根据题意,把图象分为四段,第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,第二段妈妈骑车追赶到追上小明,第三段两人稍作停留,第四段妈妈骑车返回,小明继续步行前往学校,两人同时到达.分析图象,然后选择答案.
【解答】
解:根据题意可得,与的函数关系的大致图象分为四段,
第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,两人的距离在慢慢增大,
第二段,妈妈骑车追赶到追上小明,两人的距离在减小,
第三段,两人稍作停留,两人的距离为,
第四段,妈妈骑车返回,小明继续步行前往学校,两人同时到达,两人的距离在快速增大,
纵观各选项,只有选项的图象符合.
故选B.
13.【答案】
【解析】【分析】
本题考查了幂的乘方和积的乘方的逆运算,掌握幂的乘方和积的乘方的法则是解决问题的关键.
【解答】
解:,,
,,
,
,
,
,
.
故答案为.
14.【答案】或
【解析】在运动过程中由两个位置可以使,分别作出对应的图象,根据的度数以及与间的比例求出两角的值,进而可求出角的度数.
【解答】解:当运动到如图所示的位置时,
,
,
,
,
当时,
,
如图所示,当运动到如图所示的位置时,
,
,
,
,
当时,
,
故答案为:或.
15.【答案】
【解析】解:和是同旁内角,
和是同旁内角,
和是同旁内角,
和是同旁内角,
故在标注的个角中,同旁内角有对.
故答案为:.
根据同旁内角的定义判断即可,两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的同旁,则这样一对角叫做同旁内角.
本题考查了同旁内角的定义,解题的关键是掌握同旁内角的定义,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
16.【答案】
【解析】【分析】
升高千米就可求得温度的下降值,进而求得千米处的温度.
正确理解高度每升高千米,气温下降,的含义是解题关键.
【解答】
解:高度千米与气温之间的关系式为:.
故答案为.
17.【答案】;;;
;
或或.
【解析】【分析】
本题考查了用图像表示变量之间的关系,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于表示出快车距离出发地的路程.
先得两地的距离,根据速度路程时间列式计算即可求出快车和慢车的速度;
根据两车的速度等条件可得出答案;
分别根据两车相遇前、两车相遇后以及快车从乙往甲返回途中,三种情况两车距离为时,列方程可解答.
【解答】
解:由图可知:甲乙两地之间的路程为;
快车的速度为:;
由题意得:快车小时到达甲地,则慢车小时到达甲地,
则慢车的速度为:;
故答案为:,,;
设经过小时后,快、慢两车距各自出发地的路程相等,
则
解得:,
答:出发小时,快、慢两车距各自出发地的路程相等;
故答案为:;
第一种情形第一次没有相遇前,相距,
则,
解得:,
第二种情形应是相遇后而快车没到乙地前,
解得:,
第三种情形是快车从乙往甲返回途中:,
解得:,
综上所述:快慢两车出发或或相距.
故答案为:或或.
18.【答案】解:原式
.
因为,,
所以.
原式
.
因为,
所以原式.
【解析】本题考查幂的乘方与积的乘方以及整体代入法.
先运用积的乘方法则进行计算,然后转化为已知条件,再把已知条件代入即可;
易得,,将转化为,再把已知条件代入即可解答;
先把转化为,再把已知条件代入即可解答.
19.【答案】解:大正方形的面积为:,
四部分的面积的和为:;
等式为:,
分
【解析】根据正方形的面积公式利用大正方形的边长解答,两个阴影部分长方形的面积加上两个正方形的面积进行表示;
根据大正方形的面积相等可得关于、的等式,利用等式代入数据进行计算即可求解.
本题考查了完全平方公式的几何背景,根据同一个图形的面积的不同表示方法得到等式是解题的关键.
20.【答案】证明:,于,
,,
;
在中,,
同理在中,.
又平分,
,
,
又,
.
【解析】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.
由于与都是的余角,根据同角的余角相等即可得证;
根据直角三角形两锐角互余得出,,再根据角平分线的定义得出,然后由对顶角相等的性质,等量代换即可证明.
21.【答案】,;
,;
由题意可得:
.
【解析】解:如图所示:
的邻补角为,
的邻补角为,
故答案为:,;
,,
,
,
,
,
,
,
故答案为:,;
见答案.
22.【答案】解:,
,
;
又是的平分线,
,
,
,
又是的平分线,
,
,
.
【解析】根据垂线的定义,由,得,推断出;
根据角平分线的定义,由是的平分线,得,是的平分线,得,进而解答问题.
本题考查了角平分线定义和角的有关计算.解题的关键是掌握角平分线定义和角的有关计算的方法.
23.【答案】解:;
乙的速度为:千米时,
甲出发小时后的速度为:千米时
设乙行驶小时后追上甲,
根据题意得
解得,
即乙行驶小时后追上甲,此时两人距地还有千米;
答:乙行驶小时后追上甲,此时两人距地还有千米.
【解析】本题考查了变量之间的图象:如果把自变量与因变量的每一对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形就是变量之间关系图象.
观察图象得到甲出发后小时,乙才开始出发;
根据图象得到乙用小时走了千米,甲前小时走了千米,后面小时走了千米,然后利用速度公式计算他们的速度;
设乙行驶小时后追上甲,利用他们所走路程相等列方程,然后解方程求出,再利用千米减去他们已经走的路程得到两人距地的距离.
24.【答案】解:由图象可知小明到达离家最远的地方需小时;
此时他离家千米;
设直线的解析式为,由、,
代入得:,
解得:,
故直线的解析式为:,
当时,.
答:出发两个半小时,小明离家千米;
设过、两点的直线解析式为,
由、,代入得
,
解得:,
故直线的解析式为:,
过、两点的直线解析式为,
,
分别令,则,,
解得:,,
答:小明出发小时或小时距家千米.
【解析】根据分段函数的图象上点的坐标的意义可知:小明到达离家最远的地方需小时;此时,他离家千米;
因为、在直线上,运用待定系数法求出解析式后,把代入解析式即可;
分别利用待定系数法求得过、两点的直线解析式,以及、两点的直线解析式.分别令,求解.
此题主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.
25.【答案】【小问详解】
由题意知:,.
,
,
,
,
故答案为:;
【小问详解】
,
,
,
,
故答案为:;
【小问详解】
,,,
,,
,
又,
,
,
.
【解析】【分析】因为整体图形的面积等于各部分面积之和,所以,故;
;
因为,所以,由,,,可得;
此题主要考查整式的混合运算,熟练掌握整式的混合运算是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
