西师大版五年级下册数学公因数与公倍数课件(27张PPT)
文档属性
| 名称 | 西师大版五年级下册数学公因数与公倍数课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 13:40:53 | ||
图片预览






文档简介
(共27张PPT)
公因数、公倍数
五年级下册第一单元
课堂引入
1. 拿出准备好的长方形纸片和正方形。用长3厘米、宽2厘米的长方形纸片分别铺边长6厘米、8厘米的正方形。
思考:能铺满哪个正方形?从中你发现了什么?
2.引导:(1)用长3厘米、宽2厘米的长方形纸片铺边长6厘米的正方形,每条边各铺了几次?怎样用算式表示?
(2)铺边长8厘米的正方形呢?每条边都能正好铺满吗?
学习目标
1.通过动手操作,会用列举法找公因数和公倍数。
2.通过学习,会用短除法找最大公因数和最小公倍数。
课堂引入
你发现了什么?
1
2
3
4
6
12
12的因数
30的因数
1
2
3
5
6
10
15
30
1
2
3
6
1
2
3
6
课堂探索
一张长30cm、宽12cm的长方形纸,剪成大小相等的正方形且没有剩余,这个正方形的边长最大是多少厘米?
活动一:操作小能手
活动要求
能准确的算出正方形的边长最大是多少。
活动规则
1.能准确的算出正方形的边长最大是多少。(+2)
2.汇报准确。(+1)
3.其他团队认真倾听,补充、质疑或评价。(+2)
课堂探索
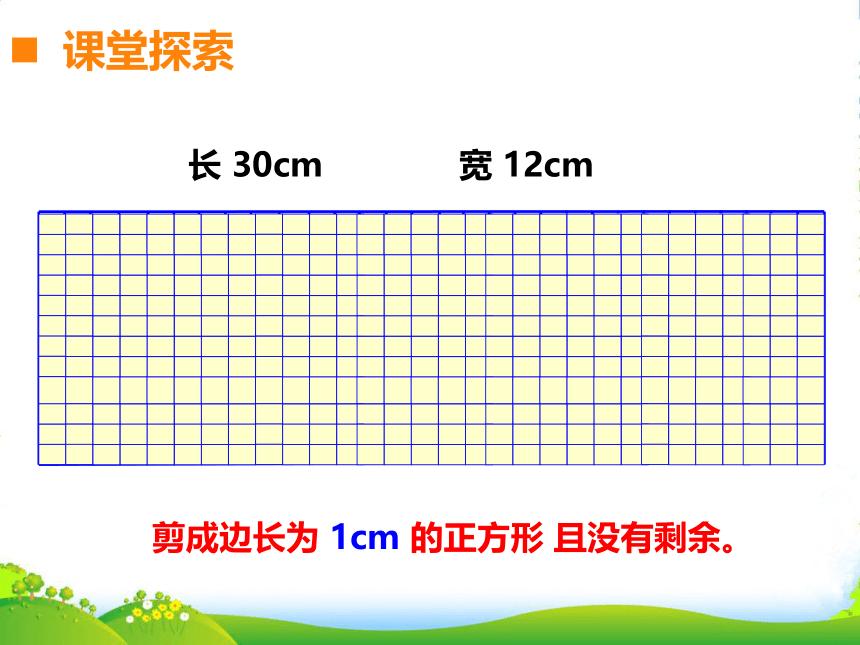
长 30cm
宽 12cm
剪成边长为 1cm 的正方形 且没有剩余。
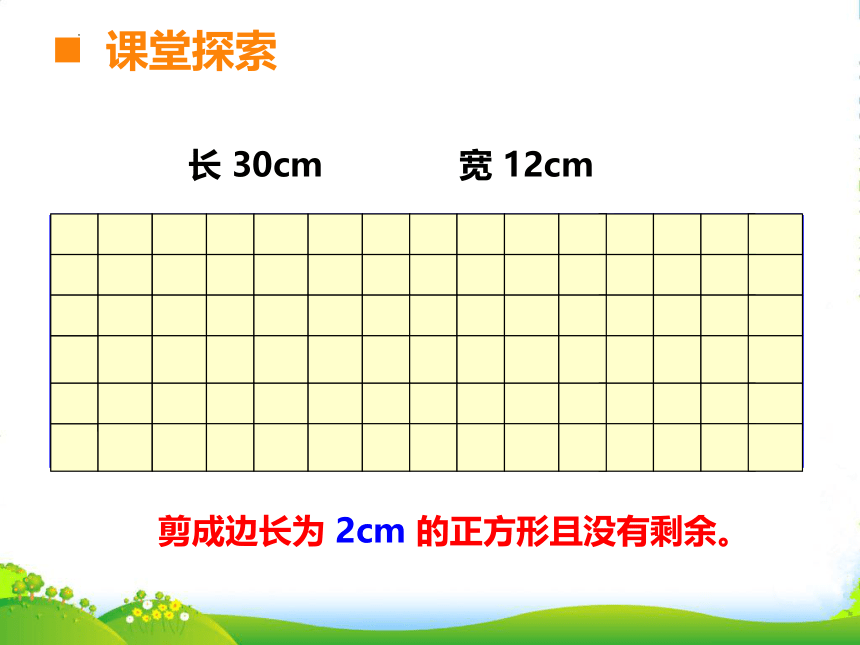
剪成边长为 2cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
课堂探索
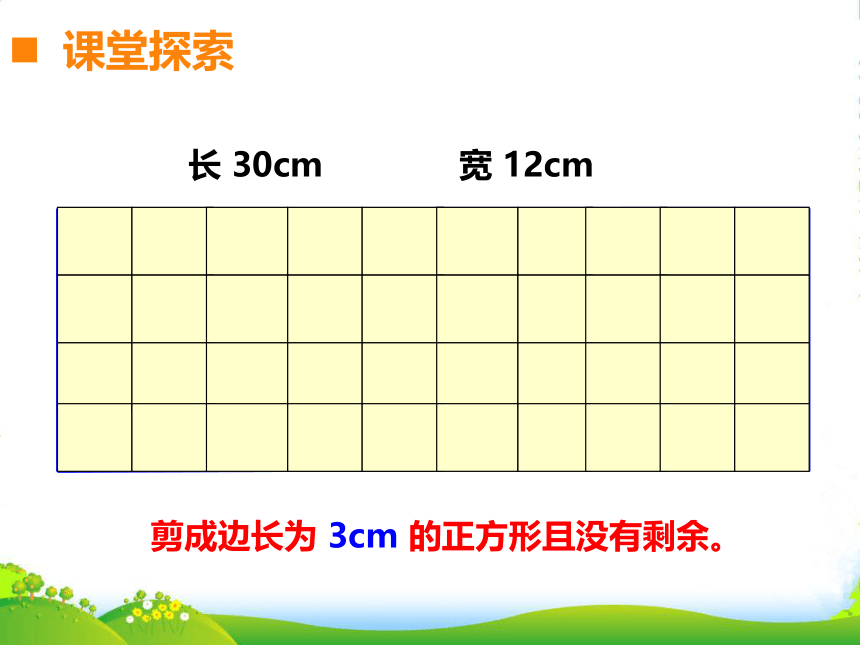
剪成边长为 3cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
剪成边长为 6cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
12的因数
30的因数
4
12
12的因数
30的因数
5
10
15
30
1
2
3
6
1
2
3
6
1
2
3
6
4
12
5
10
15
30
要使剪出的正方形大小相等且没有剩余,正方形的边长必须既是 12 的因数,又是 30 的因数。
课堂探索
1,2,3,6是12和30公有的因数,叫做它们的公因数。其中,6是最大的一个公因数,叫做它们的最大公因数。
12 和 30 公有的因数
课堂探索
12
2
3
6
2
30
2
3
15
5
思考:能不能把两个短除法合写成一个短除法。
用短除法分别找出12 和30 的因数。
可以这样求最大公因数:
课堂探索
12 30
2
3
6 15
2 5
……同时除以公因数 2
……同时除以公因数 3
……除到两个商只有公因数1为止
2
3
12 和 30 的最大公因数是:
2 ×3 = 6
课堂探索
②求出 1和8、7和9的最
大公因数。
①求出 4和8,6和12的最
大公因数 。
4和8的最大公因数:4
6和12的最大公因数:6
1和8的最大公因数:1
7和9的最大公因数:1
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1时,它们的最大公因数也是1。
从这组题中你又发现了什么?
从这组题中你发现了什么?
试一试
课堂探索
16 20
2
2
8 10
4 5
16 和 20 的最大公因数是:
2 × 2 = 4
答:最多需要4个篮子。
活动二 :学习小能手
活动要求:
1.把表补充完整。
2.议一议:你发现了什么?
评价规则:
1.补充正确。(+2)
2.能用前面分解质因数法和短除法来求最小公倍数(+2);
…
…
…
课堂引入
4的倍数
6的倍数
根据上表你会填吗?
4
8
16
20
28
32
6
18
30
42
48
54
12
24
36
12,24,36… 是 4 和 6 公有 的,叫做 4 和 6 的 。其中,12 是公倍数中最 的 值,叫做它们的 。
课堂引入
公倍数
倍数
最小公倍数
小
想一想:有最大公倍数吗?
课堂探索
可以用分解质因数的方法
4 = 2×2
6 = 2×3
4 和 6 的最小公倍数是
2
2
2×2×3 = 12
4 6
2
2 3
2
还可以写成短除法的形式
可以这样算
也可以这样算
课堂练习
1. 12的因数有( ),18的因数有( ),12和18的公因数有( ),12和18的最大公因数是( );4和20的最大公因数是( ),最小公倍数是( );8和9的最大公因数是( ),最小公倍数是( )。
2.求出下面每组数的最大公因数。
6和18 11和13 8和36
3.求出下面每组数的最小公倍数。
3和7 2和6 4和10
4.小明要把一张长96厘米,宽80厘米的长方形纸剪成面积相等的正方形而没有剩余,最少能剪多少个?
课堂练习
2. 下面哪些分数的分子、分母有公因数 2 ?哪些有
公因数 3 ?哪些有公因数 5 ?
5
6
10
15
12
21
8
10
20
30
6
18
12
18
有公因数 2 :
有公因数 3 :
有公因数 5 :
10
15
12
21
6
18
6
18
8
10
12
18
12
18
20
30
20
30
想一想:2,3,5的
倍数有哪些特征?
课堂练习
3. 五(1)班有42人、五(2)班有48人参加植树活动。要
求按班分组,如果两个班每组的人数必须相同,可
以怎样分?每组最多有多少人?
42 48
2
3
21 24
7 8
42 和 48 的最大公因数是:
2×3 = 6
42 和 48 的公因数是:1,2,3,6
答:可以每2人、3人或6人一组, 每组最多有6人。
课堂探索
找出下列每组数的最小公倍数。你发现了什么?
3 和 9 2 和 8 5 和 7 4 和 9
3 和 9 的最小公倍数是 9 。
2 和 8 的最小公倍数是 8 。
5 和 7 的最小公倍数是 35 。
4 和 9 的最小公倍数是 36 。
你发现了什么?
两个数只有公因数1时,它们的最小公倍数就是它们的乘积。
两个数是倍数关系,它们的最小公倍数就是较大的数。
9
18
27
6
12
18
课堂探索
填一填
36
45
54
63
72
81
24
30
36
42
48
54
18 ,36 ,54
18
54
36
18
54
36
18
9 6
3
3 2
3
9 和 6 的最小公倍数是
3×3×2 = 18
3
课堂练习
求下面每组数的最小公倍数。
12 和 36 ( ) 9 和 12 ( )
16 和 24 ( ) 11 和 5 ( )
36
36
48
55
通过这节课的学习,你学到了什么?
冥想
公因数、公倍数
五年级下册第一单元
课堂引入
1. 拿出准备好的长方形纸片和正方形。用长3厘米、宽2厘米的长方形纸片分别铺边长6厘米、8厘米的正方形。
思考:能铺满哪个正方形?从中你发现了什么?
2.引导:(1)用长3厘米、宽2厘米的长方形纸片铺边长6厘米的正方形,每条边各铺了几次?怎样用算式表示?
(2)铺边长8厘米的正方形呢?每条边都能正好铺满吗?
学习目标
1.通过动手操作,会用列举法找公因数和公倍数。
2.通过学习,会用短除法找最大公因数和最小公倍数。
课堂引入
你发现了什么?
1
2
3
4
6
12
12的因数
30的因数
1
2
3
5
6
10
15
30
1
2
3
6
1
2
3
6
课堂探索
一张长30cm、宽12cm的长方形纸,剪成大小相等的正方形且没有剩余,这个正方形的边长最大是多少厘米?
活动一:操作小能手
活动要求
能准确的算出正方形的边长最大是多少。
活动规则
1.能准确的算出正方形的边长最大是多少。(+2)
2.汇报准确。(+1)
3.其他团队认真倾听,补充、质疑或评价。(+2)
课堂探索
长 30cm
宽 12cm
剪成边长为 1cm 的正方形 且没有剩余。
剪成边长为 2cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
课堂探索
剪成边长为 3cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
剪成边长为 6cm 的正方形且没有剩余。
长 30cm
宽 12cm
课堂探索
12的因数
30的因数
4
12
12的因数
30的因数
5
10
15
30
1
2
3
6
1
2
3
6
1
2
3
6
4
12
5
10
15
30
要使剪出的正方形大小相等且没有剩余,正方形的边长必须既是 12 的因数,又是 30 的因数。
课堂探索
1,2,3,6是12和30公有的因数,叫做它们的公因数。其中,6是最大的一个公因数,叫做它们的最大公因数。
12 和 30 公有的因数
课堂探索
12
2
3
6
2
30
2
3
15
5
思考:能不能把两个短除法合写成一个短除法。
用短除法分别找出12 和30 的因数。
可以这样求最大公因数:
课堂探索
12 30
2
3
6 15
2 5
……同时除以公因数 2
……同时除以公因数 3
……除到两个商只有公因数1为止
2
3
12 和 30 的最大公因数是:
2 ×3 = 6
课堂探索
②求出 1和8、7和9的最
大公因数。
①求出 4和8,6和12的最
大公因数 。
4和8的最大公因数:4
6和12的最大公因数:6
1和8的最大公因数:1
7和9的最大公因数:1
当两个数成倍数关系时,较小的数就是它们的最大公因数。
当两个数只有公因数1时,它们的最大公因数也是1。
从这组题中你又发现了什么?
从这组题中你发现了什么?
试一试
课堂探索
16 20
2
2
8 10
4 5
16 和 20 的最大公因数是:
2 × 2 = 4
答:最多需要4个篮子。
活动二 :学习小能手
活动要求:
1.把表补充完整。
2.议一议:你发现了什么?
评价规则:
1.补充正确。(+2)
2.能用前面分解质因数法和短除法来求最小公倍数(+2);
…
…
…
课堂引入
4的倍数
6的倍数
根据上表你会填吗?
4
8
16
20
28
32
6
18
30
42
48
54
12
24
36
12,24,36… 是 4 和 6 公有 的,叫做 4 和 6 的 。其中,12 是公倍数中最 的 值,叫做它们的 。
课堂引入
公倍数
倍数
最小公倍数
小
想一想:有最大公倍数吗?
课堂探索
可以用分解质因数的方法
4 = 2×2
6 = 2×3
4 和 6 的最小公倍数是
2
2
2×2×3 = 12
4 6
2
2 3
2
还可以写成短除法的形式
可以这样算
也可以这样算
课堂练习
1. 12的因数有( ),18的因数有( ),12和18的公因数有( ),12和18的最大公因数是( );4和20的最大公因数是( ),最小公倍数是( );8和9的最大公因数是( ),最小公倍数是( )。
2.求出下面每组数的最大公因数。
6和18 11和13 8和36
3.求出下面每组数的最小公倍数。
3和7 2和6 4和10
4.小明要把一张长96厘米,宽80厘米的长方形纸剪成面积相等的正方形而没有剩余,最少能剪多少个?
课堂练习
2. 下面哪些分数的分子、分母有公因数 2 ?哪些有
公因数 3 ?哪些有公因数 5 ?
5
6
10
15
12
21
8
10
20
30
6
18
12
18
有公因数 2 :
有公因数 3 :
有公因数 5 :
10
15
12
21
6
18
6
18
8
10
12
18
12
18
20
30
20
30
想一想:2,3,5的
倍数有哪些特征?
课堂练习
3. 五(1)班有42人、五(2)班有48人参加植树活动。要
求按班分组,如果两个班每组的人数必须相同,可
以怎样分?每组最多有多少人?
42 48
2
3
21 24
7 8
42 和 48 的最大公因数是:
2×3 = 6
42 和 48 的公因数是:1,2,3,6
答:可以每2人、3人或6人一组, 每组最多有6人。
课堂探索
找出下列每组数的最小公倍数。你发现了什么?
3 和 9 2 和 8 5 和 7 4 和 9
3 和 9 的最小公倍数是 9 。
2 和 8 的最小公倍数是 8 。
5 和 7 的最小公倍数是 35 。
4 和 9 的最小公倍数是 36 。
你发现了什么?
两个数只有公因数1时,它们的最小公倍数就是它们的乘积。
两个数是倍数关系,它们的最小公倍数就是较大的数。
9
18
27
6
12
18
课堂探索
填一填
36
45
54
63
72
81
24
30
36
42
48
54
18 ,36 ,54
18
54
36
18
54
36
18
9 6
3
3 2
3
9 和 6 的最小公倍数是
3×3×2 = 18
3
课堂练习
求下面每组数的最小公倍数。
12 和 36 ( ) 9 和 12 ( )
16 和 24 ( ) 11 和 5 ( )
36
36
48
55
通过这节课的学习,你学到了什么?
冥想
