18.2.3 正方形 课件(41张ppt)2023—2024学年人教版八年级数学下册
文档属性
| 名称 | 18.2.3 正方形 课件(41张ppt)2023—2024学年人教版八年级数学下册 |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览




文档简介
(共41张PPT)
《正方形》说课
A
B
C
D
O
教材分析
教学
目标
重点
难点
《正方形》是人教版八年级下册第十八章的内容,它是学生学习了菱形、矩形后的又一类特殊的平行四边形,是在学生初步具备观察、操作、类比分析等活动经验的基础上出现的。目的在于让学生通过研究正方形的性质和判定方法及其运用,进一步发展几何直觉和逻辑推理能力,逐步掌握说理的基本方法。这一节课既是前面所学知识的延续,也是对平行四边形、菱形、矩形的概括与升华,又为学习立体几何有关知识打下基础。因此,学好本节尤为重要。
教法
学法
教学
准备
。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
重点:探索正方形的性质与判定。
难点:正方形的性质和判定方法的具体运用。
关键:把握正方形既是特殊矩形又是特殊菱形这一特性来学习本节内容。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
针对本节课特点,结合学生已有的知识经验,我引领学生联系前面所学知识,沿着研究平面图形的基本思路(先概念后性质再判定),利用类比学习法,通过“动手操作、观察分析、总结归纳、简单运用”开展教与学。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
教师准备:
一张矩形纸片、一个菱形 活动框架,三角板、圆规和制作的课件。
学生准备:
课前复习平行四边形、矩形、菱形的定义、性质及判定方法,自备一张长方形纸和作图工具。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
操作实验
教学流程
探究性质
探究判定方法
综合运用
拓展创新
判定方法的应用
(得出正方形的定义,正方形与矩形、菱形、平行四边形之间的关系)
性质运用
1、怎样用一张矩形的纸片折出一个正方形?
2、怎样将一个菱形的木框变成一个正方形木框?
操作实验
正方形
矩形
实验与观察一:折叠矩形纸片
正方形的定义:一组邻边相等的矩形叫做正方形。
正方形
菱形
实验与观察二:转动菱形模型
思考:平行四边形、矩形、菱形、正方形的关系?
正方形既是邻边相等的特殊矩形,又是有一个角是直角的特殊菱形。
平行四边形
矩形
菱形
正方形
折叠矩形纸片
演示菱形模型
A
B
C
D
O
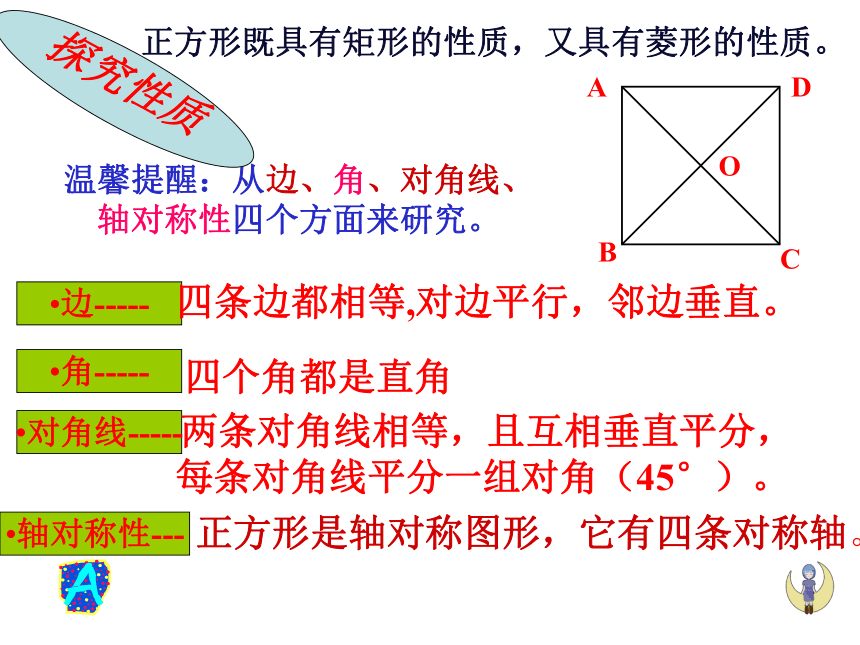
温馨提醒:从边、角、对角线、轴对称性四个方面来研究。
边-----
角-----
对角线-----
四条边都相等,对边平行,邻边垂直。
四个角都是直角
两条对角线相等,且互相垂直平分,每条对角线平分一组对角(45°)。
探究性质
正方形是轴对称图形,它有四条对称轴。
轴对称性---
正方形既具有矩形的性质,又具有菱形的性质。
1.正方形具有而菱形不具有的
性质是( )
A.对角线互相垂直
B.四条边都相等
C.对角线相等
D.对角线互相平分
C
学以致用
2、正方形具有而矩形不具有的性质是( )
A、四个角都是直角
B、对角线相等
C、对角线互相平分
D、对角线互相垂直
D
3.四个内角都相等的四边形一
定是( )
A.正方形
B.菱形
C.矩形
D.平行四边形
C
4、如图E是正方形ABCD内一
点,且△EAD是等边三角形
E
C
B
A
D
1
则∠1=___
750
5、如图正方形ABCD中,
若E为AC上一点, 且BE=6cm,则DE=____
E
O
C
B
A
D
6cm
6、正方形ABCD的对角线的长为10,
M是AB边上的一点,且ME⊥AC于E,
MF⊥BD于 F.则ME+MF=___
F
E
M
C
B
A
D
O
5
1、具备什么样条件的矩形是正方形?
矩形ABCD中,对角线AC、BD交于点O,若__________,则ABCD为正方形.
O
C
D
A
B
结论1. 有一组邻边相等的矩形是正方形。
结论2. 对角线互相垂直的矩形是正方形。
AB=BC
AC⊥BD
探究判定方法
菱形ABCD中,对角线AC、BD交于点O,若______________, 则ABCD为正方形.
A
O
C
D
B
2、具备什么样条件的菱形是正方形?
结论2、 对角线相等的菱形是正方形。
结论1、 有一个角是直角的菱形是正方形。
∠ABC=
900
AC=BD
正方形的常用判定方法
1、 有一组邻边相等的矩形是正方形。
2、 对角线互相垂直的矩形是正方形。
判定一:
判定二
判定三:
3、 有一个角是直角的菱形是正方形。
判定四:
4、 对角线相等的菱形是正方形。
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
有一个角是直角且有一组邻边相等
两对角线相等
两对角线互垂直
两对角线互相垂直且相等
两对角线互垂直
两对角线相等
3、如何判定一个平行四边形是正方形?
1、下列说法中,正确的是( )
A.对角线相等的四边形是正方形
B.垂直的平行四边形是正方形
C.对角线相等且相互平分的平行四边形是正方形
D.对角线相等且垂直的平行四边形是正方形
D
2、在四边形ABCD中,O是对角线的交点,能判定这个四边形为正方形的是( )
A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ,∠A=∠C
C.AO=CO,BO=DO,AB=BC
D.AC=BD
O
C
B
A
D
A
学以致用
3、填空
一组邻边_____的菱形是正方形。
一组邻边_____的矩形是正方形。
一组邻边_____的平行四边形形是正方形。
对角线_______的菱形是正方形。
对角线_______的矩形是正方形。
对角线_______的平行四边形是正方形。
对角线_______的四边形是正方形。
1、如图,已知四边形ABCD是正方形,且AE=BF=CG=DH。求证:四边形EFGH是正方形。
H
G
F
E
D
C
B
A
证题思路分析
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
综合运用
2、作图(保留作图痕迹)
(1)以4㎝长线段为边,画一个正方形。
(2)以6㎝长的线段为对角线,画一个正方形。
一位女士想买一条方纱巾,有一天她在商店里看到一块漂亮的纱巾,非常想买,但她拿起来看时感觉纱巾不太方,商店老板看她犹豫不决的样子,马上过来拉起一组对角,让女士看另一组对角是否对齐,女士还有些疑惑,老板又拉起另一组对角让女士检验,女士终于买下这块纱巾,你认为女士买的这块纱巾是正方形的吗?
拓展创新
课堂小结(回顾本节所学知识)
正方形的定义:
正方形性质
正方形判定方法
正方形与平行四边形、菱形、矩形的关系
法1、有一组邻边相等的矩形是正方形。
2、四个角都是直角
1、四条边都相等,对边平行,邻边垂直。
3、两条对角线相等且互相垂直平分,
每条对角线平分一组对角。
法4、对角线相等的菱形是正方形。
法3、有一个教是直角的菱形是正方形。
法2、对角线互相垂直的矩形是正方形。
一组邻边相等的矩形叫做正方形。
4、正方形是轴对称图形它有四条对称轴。
作业布置
(小页试卷)
1、(1)一个正方形的面积为4,
则其对角线的长为___
(2)一个正方形的对角线为4
则其面积为___
√
2
2
8
2.如图E是正方形ABCD外一点,
且△ADE是等边三角形,则
E
C
B
A
D
(2)∠DEC=__
(1)∠EAC=__
1050
150
3、如图E是正方形ABCD内一
点,且△EAD是等边三角形
E
C
B
A
D
1
则∠1=___
750
4、正方形ABCD的对角线的长为10,
M是AB边上的一点,且ME⊥AC于E,
MF⊥BD于 F.则ME+MF=___
F
E
M
C
B
A
D
O
5
5.(1)如图正方形ABCD中,对角线交于点O,则图中共有
__个等腰直角三角形.
O
C
B
A
D
8
(2)如图正方形ABCD中,
若E为AC上一点, 且BE=6cm,则DE=____
E
O
C
B
A
D
6cm
(3)如图正方形ABCD中,
若E为AC上一点,
且BE=6cm,
则FG=____
G
F
E
C
B
A
D
过E作
EF⊥CD于F,EG⊥AD于G
6cm
6、如图,已知正方形ABCD内有一个△BEF,AB=6,AF︰FD=1︰2,E为DC的中点,求△BEF的面积。
A
B
C
D
F
E
7.四边形ABCD是正方形,点G为BC上任意一点(点G与B,C不重合),AE⊥DG于点E,
CF//AE交DG于点F.
(1).在图中找出一对全等三角形,并加以证明;
(2).求证:AE=FC+EF.
G
8、如图,以锐角△ABC的边AC,AB为边向外作正方形ACDE和正方形ABGF,连接BE,CF.
(1).试探索BE和CF的大小关系?并说明理。
(2).你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角。
变式1:四边形ABCD和MBNP都是正方形。AM=CN成立吗,为什么?
变式2:四边形ABCD和四边形BEFG都是正方形,连接AG、EC。
(1)观察猜想AG与CE之间大小关系。
(2)延长AG交CE于点M,AM与CE是怎样的位置关系。
《正方形》说课
A
B
C
D
O
教材分析
教学
目标
重点
难点
《正方形》是人教版八年级下册第十八章的内容,它是学生学习了菱形、矩形后的又一类特殊的平行四边形,是在学生初步具备观察、操作、类比分析等活动经验的基础上出现的。目的在于让学生通过研究正方形的性质和判定方法及其运用,进一步发展几何直觉和逻辑推理能力,逐步掌握说理的基本方法。这一节课既是前面所学知识的延续,也是对平行四边形、菱形、矩形的概括与升华,又为学习立体几何有关知识打下基础。因此,学好本节尤为重要。
教法
学法
教学
准备
。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
重点:探索正方形的性质与判定。
难点:正方形的性质和判定方法的具体运用。
关键:把握正方形既是特殊矩形又是特殊菱形这一特性来学习本节内容。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
针对本节课特点,结合学生已有的知识经验,我引领学生联系前面所学知识,沿着研究平面图形的基本思路(先概念后性质再判定),利用类比学习法,通过“动手操作、观察分析、总结归纳、简单运用”开展教与学。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
教师准备:
一张矩形纸片、一个菱形 活动框架,三角板、圆规和制作的课件。
学生准备:
课前复习平行四边形、矩形、菱形的定义、性质及判定方法,自备一张长方形纸和作图工具。
教材分析
教学
目标
重点
难点
教法
学法
教学
准备
操作实验
教学流程
探究性质
探究判定方法
综合运用
拓展创新
判定方法的应用
(得出正方形的定义,正方形与矩形、菱形、平行四边形之间的关系)
性质运用
1、怎样用一张矩形的纸片折出一个正方形?
2、怎样将一个菱形的木框变成一个正方形木框?
操作实验
正方形
矩形
实验与观察一:折叠矩形纸片
正方形的定义:一组邻边相等的矩形叫做正方形。
正方形
菱形
实验与观察二:转动菱形模型
思考:平行四边形、矩形、菱形、正方形的关系?
正方形既是邻边相等的特殊矩形,又是有一个角是直角的特殊菱形。
平行四边形
矩形
菱形
正方形
折叠矩形纸片
演示菱形模型
A
B
C
D
O
温馨提醒:从边、角、对角线、轴对称性四个方面来研究。
边-----
角-----
对角线-----
四条边都相等,对边平行,邻边垂直。
四个角都是直角
两条对角线相等,且互相垂直平分,每条对角线平分一组对角(45°)。
探究性质
正方形是轴对称图形,它有四条对称轴。
轴对称性---
正方形既具有矩形的性质,又具有菱形的性质。
1.正方形具有而菱形不具有的
性质是( )
A.对角线互相垂直
B.四条边都相等
C.对角线相等
D.对角线互相平分
C
学以致用
2、正方形具有而矩形不具有的性质是( )
A、四个角都是直角
B、对角线相等
C、对角线互相平分
D、对角线互相垂直
D
3.四个内角都相等的四边形一
定是( )
A.正方形
B.菱形
C.矩形
D.平行四边形
C
4、如图E是正方形ABCD内一
点,且△EAD是等边三角形
E
C
B
A
D
1
则∠1=___
750
5、如图正方形ABCD中,
若E为AC上一点, 且BE=6cm,则DE=____
E
O
C
B
A
D
6cm
6、正方形ABCD的对角线的长为10,
M是AB边上的一点,且ME⊥AC于E,
MF⊥BD于 F.则ME+MF=___
F
E
M
C
B
A
D
O
5
1、具备什么样条件的矩形是正方形?
矩形ABCD中,对角线AC、BD交于点O,若__________,则ABCD为正方形.
O
C
D
A
B
结论1. 有一组邻边相等的矩形是正方形。
结论2. 对角线互相垂直的矩形是正方形。
AB=BC
AC⊥BD
探究判定方法
菱形ABCD中,对角线AC、BD交于点O,若______________, 则ABCD为正方形.
A
O
C
D
B
2、具备什么样条件的菱形是正方形?
结论2、 对角线相等的菱形是正方形。
结论1、 有一个角是直角的菱形是正方形。
∠ABC=
900
AC=BD
正方形的常用判定方法
1、 有一组邻边相等的矩形是正方形。
2、 对角线互相垂直的矩形是正方形。
判定一:
判定二
判定三:
3、 有一个角是直角的菱形是正方形。
判定四:
4、 对角线相等的菱形是正方形。
平行四边形
矩形
菱形
正方形
有一个角是直角
有一组邻边相等
有一个角是直角
有一组邻边相等
有一个角是直角且有一组邻边相等
两对角线相等
两对角线互垂直
两对角线互相垂直且相等
两对角线互垂直
两对角线相等
3、如何判定一个平行四边形是正方形?
1、下列说法中,正确的是( )
A.对角线相等的四边形是正方形
B.垂直的平行四边形是正方形
C.对角线相等且相互平分的平行四边形是正方形
D.对角线相等且垂直的平行四边形是正方形
D
2、在四边形ABCD中,O是对角线的交点,能判定这个四边形为正方形的是( )
A.AO=BO=CO=DO,AC⊥BD
B.AD∥BC ,∠A=∠C
C.AO=CO,BO=DO,AB=BC
D.AC=BD
O
C
B
A
D
A
学以致用
3、填空
一组邻边_____的菱形是正方形。
一组邻边_____的矩形是正方形。
一组邻边_____的平行四边形形是正方形。
对角线_______的菱形是正方形。
对角线_______的矩形是正方形。
对角线_______的平行四边形是正方形。
对角线_______的四边形是正方形。
1、如图,已知四边形ABCD是正方形,且AE=BF=CG=DH。求证:四边形EFGH是正方形。
H
G
F
E
D
C
B
A
证题思路分析
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
综合运用
2、作图(保留作图痕迹)
(1)以4㎝长线段为边,画一个正方形。
(2)以6㎝长的线段为对角线,画一个正方形。
一位女士想买一条方纱巾,有一天她在商店里看到一块漂亮的纱巾,非常想买,但她拿起来看时感觉纱巾不太方,商店老板看她犹豫不决的样子,马上过来拉起一组对角,让女士看另一组对角是否对齐,女士还有些疑惑,老板又拉起另一组对角让女士检验,女士终于买下这块纱巾,你认为女士买的这块纱巾是正方形的吗?
拓展创新
课堂小结(回顾本节所学知识)
正方形的定义:
正方形性质
正方形判定方法
正方形与平行四边形、菱形、矩形的关系
法1、有一组邻边相等的矩形是正方形。
2、四个角都是直角
1、四条边都相等,对边平行,邻边垂直。
3、两条对角线相等且互相垂直平分,
每条对角线平分一组对角。
法4、对角线相等的菱形是正方形。
法3、有一个教是直角的菱形是正方形。
法2、对角线互相垂直的矩形是正方形。
一组邻边相等的矩形叫做正方形。
4、正方形是轴对称图形它有四条对称轴。
作业布置
(小页试卷)
1、(1)一个正方形的面积为4,
则其对角线的长为___
(2)一个正方形的对角线为4
则其面积为___
√
2
2
8
2.如图E是正方形ABCD外一点,
且△ADE是等边三角形,则
E
C
B
A
D
(2)∠DEC=__
(1)∠EAC=__
1050
150
3、如图E是正方形ABCD内一
点,且△EAD是等边三角形
E
C
B
A
D
1
则∠1=___
750
4、正方形ABCD的对角线的长为10,
M是AB边上的一点,且ME⊥AC于E,
MF⊥BD于 F.则ME+MF=___
F
E
M
C
B
A
D
O
5
5.(1)如图正方形ABCD中,对角线交于点O,则图中共有
__个等腰直角三角形.
O
C
B
A
D
8
(2)如图正方形ABCD中,
若E为AC上一点, 且BE=6cm,则DE=____
E
O
C
B
A
D
6cm
(3)如图正方形ABCD中,
若E为AC上一点,
且BE=6cm,
则FG=____
G
F
E
C
B
A
D
过E作
EF⊥CD于F,EG⊥AD于G
6cm
6、如图,已知正方形ABCD内有一个△BEF,AB=6,AF︰FD=1︰2,E为DC的中点,求△BEF的面积。
A
B
C
D
F
E
7.四边形ABCD是正方形,点G为BC上任意一点(点G与B,C不重合),AE⊥DG于点E,
CF//AE交DG于点F.
(1).在图中找出一对全等三角形,并加以证明;
(2).求证:AE=FC+EF.
G
8、如图,以锐角△ABC的边AC,AB为边向外作正方形ACDE和正方形ABGF,连接BE,CF.
(1).试探索BE和CF的大小关系?并说明理。
(2).你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角。
变式1:四边形ABCD和MBNP都是正方形。AM=CN成立吗,为什么?
变式2:四边形ABCD和四边形BEFG都是正方形,连接AG、EC。
(1)观察猜想AG与CE之间大小关系。
(2)延长AG交CE于点M,AM与CE是怎样的位置关系。
