2024辽宁中考数学二轮中考考点研究 2.4 不等式(组)的解法及不等式的应用 (课件) 47张PPT
文档属性
| 名称 | 2024辽宁中考数学二轮中考考点研究 2.4 不等式(组)的解法及不等式的应用 (课件) 47张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 322.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览







文档简介
(共47张PPT)
第四节 不等式(组)的解法及不等式的应用
辽宁近年中考真题精选
1
考点精讲
2
重难点分层练
3
辽宁近年中考真题精选
1
命题点
解一元一次不等式及解集表示
1. (2020沈阳6题2分)不等式2x≤6的解集是( )
A. x≤3 B. x≥3 C. x<3 D. x>3
A
2. (2020辽宁4题3分)不等式4x+1>x+7的解集在数轴上表示正确的是( )
A
2
命题点
解一元一次不等式组及解集表示
类型一 求不等式组的解集
3. (2023抚顺12题3分)不等式组 的解集是________.
4. (2021沈阳12题3分)不等式组 的解集是________.
2x-3≥5
x-2≥0
x-5<1
3x-5≥0
x≥4
≤x<6
辽宁其他地市真题
5. (2023盘锦6题3分)不等式组 的解集是( )
A. -1<x≤3 B. 1≤x<3
C. -1≤x<3 D. 1<x≤3
6. (2022盘锦15题3分)不等式组 的解集是________.
2(x+2)+1≥3
2x+3≤x+11
-1>2-x
C
类型二 不等式组的解集表示
7. (2023抚顺5题3分)一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A. -1B. -1≤x<2
C. -1D. 无解
第7题图
A
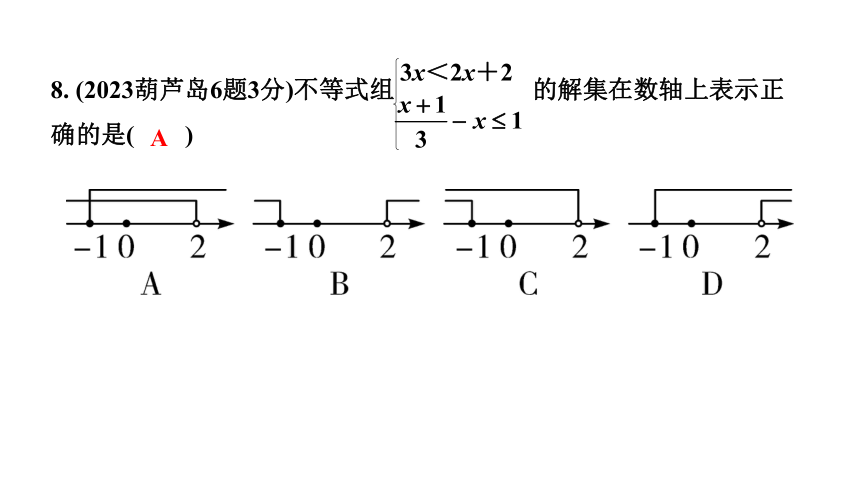
8. (2023葫芦岛6题3分)不等式组 的解集在数轴上表示正确的是( )
3x<2x+2
A
类型三 求不等式组的整数解
9. (2022铁岭葫芦岛6题3分)不等式组 的整数解的个数是( )
A. 2
B. 3
C. 4
D. 5
3+x>1
2x-3≤1
C
3
命题点
一元一次不等式的实际应用(沈阳3考;抚顺、铁岭、辽阳近5年连续考查;本溪2考;葫芦岛4考)
10. 小明要代表班级参加学校举办的消防知识竞赛,共有25道题,规定答对一道题得6分,答错或不答一道题扣2分,只有得分超过90分才能获得奖品,问小明至少答对多少道题才能获得奖品?
解:设小明答对x道题,则答错或不答(25-x)道题,
根据题意,
得6x-2(25-x)>90,
解得x>17 ,
∵x为非负整数,
∴x的最小值为18.
答:小明至少答对18道题才能获得奖品.
11. (2023抚顺21题12分)为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境,若种植甲种花卉2平方米,乙种花卉3平方米,共需430元;种植甲种花卉1平方米,乙种花卉2平方米,共需260元.
(1)求该社区种植甲种花卉1平方米和种植乙种花卉1平方米各需多少元?
解:(1)设种植甲种花卉1平方米需x元,种植乙种花卉1平方米需y元.
由题意得 ,
解得 .
答:该社区种植甲种花卉1平方米需80元,种植乙种花卉1平方米需90元;
(2)设能种植乙种花卉m平方米,则种植甲种花卉(75-m)平方米.
由题意,得80(75-m)+90m≤6300,
解得m≤30.
答:最多能种植乙种花卉30平方米.
(2)该社区准备种植两种花卉共75平方米且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
12. (2021抚顺铁岭21题12分)某市公交公司为落实“绿色出行,低碳环保”的城市发展理念,计划购买A,B两种型号的新型公交车.已知购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(1)求A型公交车和B型公交车每辆各多少万元?
解:(1)设A型公交车每辆x万元,B型公交车每辆y万元,根据题意得
,
解得 ,
答:A型公交车每辆45万元,B型公交车每辆60万元;
(2)公交公司计划购买A型公交车和B型公交车共140辆,且购买A型公交车的总费用不高于B型公交车的总费用,那么该公司最多购买多少辆A型公交车?
(2)设该公司购买m辆A型公交车,则购买(140-m)辆B型公交车,
根据题意得45m≤60(140-m),
解得m≤80,
∴m的最大值是80,
答:该公司最多购买80辆A型公交车.
13. (2021本溪辽阳葫芦岛21题12分)某班计划购买两种毕业纪念册,已知购买1本手绘纪念册和4本图片纪念册共需135元,购买5本手绘纪念册和2本图片纪念册共需225元.
(1)求每本手绘纪念册和每本图片纪念册的价格分别为多少元?
解:(1)设每本手绘纪念册的价格为x元,每本图片纪念册的价格为y元,根据题意得 ,
解得 ,
答:每本手绘纪念册的价格为35元,每本图片纪念册的价格为25元;
(2)设购买手绘纪念册a本,则购买图片纪念册(40-a)本,根据题意得,
35a+25(40-a)≤1100,
解得a≤10.
答:最多能购买手绘纪念册10本.
(2)该班计划购买手绘纪念册和图片纪念册共40本,总费用不超过1100元,那么最多能购买手绘纪念册多少本?
14. (2023辽阳21题12分)为提高中小学生的身体素质,各校大力开展校园足球活动.某体育用品商店抓住这一商机,第一次用30000元购进A,B两种型号的足球,并很快销售完毕,共获利12200元.其进价和售价如下表:
AA B
进价(元/个) 120 200
售价(元/个) 170 280
型号
价格
(1)该体育用品商店购进A,B两种型号的足球各多少个?
解:(1)设购进A种型号的足球x个,B种型号的足球y个.根据题意列方程组,得 ,
解得 ,
答:该体育用品商店购进A种型号的足球100个,B种型号的足球90个;
(2)设第二次购进A种型号的足球a个,则购进B种型号的足球(260-a)个.根据题意,得
120a+200(260-a)≤40000.
解得a≥150.
答:最少购进A种型号的足球150个.
(2)该体育用品商店第二次准备用不超过40000元的资金再次购进A,B两种型号的足球共260个,最少购进A种型号的足球多少个?
15. (2022抚顺22题12分)为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
解:(1)设乙工程队每天能改造道路的长度是x米,则甲工程队每天能改造道路的长度是 x米,
根据题意得 ,
解得x=40,
经检验,x=40是原分式方程的解,且符合实际.
∴ x= ×40=60(米).
答:甲工程队每天能改造道路的长度是60米,乙工程队每天能改造道路的长度是40米;
(2)设安排甲队工作m天,则乙队需工作 天,根据题意得7m+5× ≤145,解得m≥10.
答:至少安排甲队工作10天.
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
一元一次不等式
的实际应用的一
般解题步骤
性质1
性质2
性质3
不等式的
基本性质
一元一次不等式的
解法及解集表示
一般步骤
解集在数轴
上的表示
一元一次不等式组
的解法及解集表示
一般步骤
解集的类型
及其表示
不等式(组)
的解法及
不等式的应用
考点精讲
【对接教材】北师:八下第二章P36~P63;
人教:七下第九章P113~P133.
不等式的基本性质
性质1:不等式两边都加(或减)同一个整式,不等号的方向不变, 即如果a>b,那么a±c____ b±c
性质2:________________________________________________ ,
即如果a>b,c>0,那么ac______ bc(或 ____ )
性质3:________________________________________________ , 即如果a>b,c<0,那么ac______bc(或 ____ )
口诀:负变正不变
>
不等式两边乘(或除以)同一个正数,不等号的方向不变
>
>
不等式两边乘(或除以)同一个负数,不等号的方向改变
<
<
一元一次不等式的解法及解集表示
一般步骤:去分母,去括号,移项,合并同类项,系数化为1(注意不等号方向是否改变)
解集 在数轴上的表示 注意事项
x”“<”用_________ ; “<”“≤”开口向____ , “>”“≥”开口向_____
x>a x≤a x≥a 空心圆圈
左
右
解集在数轴上的表示
一元一次不等式组的解法及解集表示
一般步骤:先分别解各个不等式→在数轴上表示出各不等式的解集→确定解 集的公共部分,即为不等式组的解集
解集的类型及其表示
类型(a>b) 解集 在数轴上的表示 口诀
同大取大
同小取小
大小小大 取中间
大大小小 取不了
x≥a
x>b
x≤a
xxx≥b
x>a
x≤b
_________
_________
_________
_________
x≥a
xb≤x无解
一元一次不等式 的实际应用的一 般解题步骤
1.找:找出题目中的不等关系(正确理解表示不等关系的关键词的意义:例如:“至少” (≥)、“最多”(≤)、“不低于”(≥)、“不高于”(≤)、“不大于”(≤)、“不小于” (≥)等)
2.设:设未知数
3.列:根据不等关系,列出不等式
4.解:解不等式
5.验:取值要符合实际意义
6.答:根据题意作答
●
易错警示
1.题目中出现一些不等关系的关键词时,在设未知数时不能出现表示不等关 系的关键词;
2.要注意所取值要符合实际意义,例如:人数必为正整数,当x 表示人数, 且x≥3 时,则x 的最小值为4,即至少有4人
一元一次不等式 的实际应用的一 般解题步骤
重难点分层练
一、一元一次不等式(组)的解法及解集表示
回顾必备知识
一题多设问
例1
已知不等式组
>1①
4(x-1)≤2(x-a)②
例1题图
(1)解不等式①的解集为________;
(2)解不等式②的解集为________;
(3)若a=-3,则该不等式组的解集为________,并将解集在数轴上表示出来;
(4)若该不等式组有3个整数解,则a的取值范围为___________.
x>4
x≤2-a
4<x≤5
-6体验辽宁考法
1. (2023沈阳铁西区二模)不等式组 的整数解的个数是( )
A. 无数个 B. 3 C. 4 D. 5
x+1>0
≥2x-1
C
2. 不等式组
2(x-1)<0
3x+1≥2x
的解集在数轴上表示正确的是( )
A
二、一元一次不等式的实际应用
回顾必备知识
例2 根据题意列不等式.
(1)“7与m的和大于3”用不等式表示为________;
(2)“y的2倍与8的和不小于-3”用不等式表示为__________;
(3)“x的 与x的和不超过5”用不等式表示为___________;
(4)“a的2倍减去3的差是一个非负数”用不等式表示为________;
(5)“x的3倍与8的和比x的5倍大”,用不等式表示为___________.
7+m>3
2y+8≥-3
x+x≤5
2a-3≥0
3x+8>5x
品名 批发价(元/个) 零售价(元/个)
A种工艺品 130 160
B种工艺品 100 120
例3 某工艺品商店采购员要到厂家批发①采购A、B两种工艺品100个,②付款总额不得超过11800元,已知两种工艺品厂家的批发价和商店的零售价如下表,试解答下列问题:
提升关键能力
(1)该采购员最多可采购A种工艺品多少个?
解:(1)设采购员购进A种工艺品x个,则购进B种工艺品(100-x)个,
由题意得130x+100(100-x)≤11800,
解得x≤60,
答:采购员最多可购进A种工艺品60个;
【分层分析】(1)设采购员可采购A种工艺品x个,根据信息①可知采购B种工艺品(100-x)个,根据信息②列出不等式_________________
_______________________;
130x+100(100-x)≤11800
(2)若该商店③把100个工艺品全部以零售价售出,为使商场获得④利润不低于2585元,则最少采购A种工艺品多少个?
(2)设采购A种工艺品y个,根据信息③可知采购B种工艺品(100-y)个,根据信息④可列不等式_____________________________________.
(160-130)y+(120-100)(100-y)≥2585
(2)设采购A种工艺品y个.
则彩购B种工艺品(100-y)个,根据题意得
(160-130)y+(120-100)(100-y)≥2585,
解得y≥58.5,
∵工艺品的个数为整数,
∴y最小取59.
答:最少采购A种工艺品59个.
●
易错警示
在解答不等式的实际应用时,不等式的结果要满足实际情况(比如人数,篮球的个数等),对于不能取小数的情况,根据实际取最近的整数.
体验辽宁考法
3. 某中学团委组织七年级和八年级共60名学生参加环保活动,七年级学生平均收集15个废弃塑料瓶,八年级学生平均收集20个废弃塑料瓶,为了保证收集废弃塑料瓶总数不少于1000个,至少需要多少八年级学生参加活动?
解:设参加活动的八年级学生为x个,则参加活动的七年级学生为(60-x)个,由题意,得
20x+15(60-x)≥1000,
解得x≥20.
∴至少需要20名八年级学生参加活动.
4. (2021沈阳铁西区期中)某中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元.
(1)求每个大地球仪和每个小地球仪各多少元?
解:(1)设每个大地球仪x元,每个小地球仪y元,根据题意可得,
解得
答:每个大地球仪52元,每个小地球仪28元;
(2)设购买大地球仪a个,则购买小地球仪(30-a)个,根据题意可得:52a+28(30-a)≤980,
解得a≤5 ,
∴30-a≥24 ,
∵小地球仪的个数为整数,
∴(30-a)最小取25.
答:至少要购买25个小地球仪.
(2)该中学决定购买以上两种地球仪共30个,总费用不超过980元,那么至少要购买多少个小地球仪?
第四节 不等式(组)的解法及不等式的应用
辽宁近年中考真题精选
1
考点精讲
2
重难点分层练
3
辽宁近年中考真题精选
1
命题点
解一元一次不等式及解集表示
1. (2020沈阳6题2分)不等式2x≤6的解集是( )
A. x≤3 B. x≥3 C. x<3 D. x>3
A
2. (2020辽宁4题3分)不等式4x+1>x+7的解集在数轴上表示正确的是( )
A
2
命题点
解一元一次不等式组及解集表示
类型一 求不等式组的解集
3. (2023抚顺12题3分)不等式组 的解集是________.
4. (2021沈阳12题3分)不等式组 的解集是________.
2x-3≥5
x-2≥0
x-5<1
3x-5≥0
x≥4
≤x<6
辽宁其他地市真题
5. (2023盘锦6题3分)不等式组 的解集是( )
A. -1<x≤3 B. 1≤x<3
C. -1≤x<3 D. 1<x≤3
6. (2022盘锦15题3分)不等式组 的解集是________.
2(x+2)+1≥3
2x+3≤x+11
-1>2-x
C
7. (2023抚顺5题3分)一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
A. -1
C. -1
第7题图
A
8. (2023葫芦岛6题3分)不等式组 的解集在数轴上表示正确的是( )
3x<2x+2
A
类型三 求不等式组的整数解
9. (2022铁岭葫芦岛6题3分)不等式组 的整数解的个数是( )
A. 2
B. 3
C. 4
D. 5
3+x>1
2x-3≤1
C
3
命题点
一元一次不等式的实际应用(沈阳3考;抚顺、铁岭、辽阳近5年连续考查;本溪2考;葫芦岛4考)
10. 小明要代表班级参加学校举办的消防知识竞赛,共有25道题,规定答对一道题得6分,答错或不答一道题扣2分,只有得分超过90分才能获得奖品,问小明至少答对多少道题才能获得奖品?
解:设小明答对x道题,则答错或不答(25-x)道题,
根据题意,
得6x-2(25-x)>90,
解得x>17 ,
∵x为非负整数,
∴x的最小值为18.
答:小明至少答对18道题才能获得奖品.
11. (2023抚顺21题12分)为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境,若种植甲种花卉2平方米,乙种花卉3平方米,共需430元;种植甲种花卉1平方米,乙种花卉2平方米,共需260元.
(1)求该社区种植甲种花卉1平方米和种植乙种花卉1平方米各需多少元?
解:(1)设种植甲种花卉1平方米需x元,种植乙种花卉1平方米需y元.
由题意得 ,
解得 .
答:该社区种植甲种花卉1平方米需80元,种植乙种花卉1平方米需90元;
(2)设能种植乙种花卉m平方米,则种植甲种花卉(75-m)平方米.
由题意,得80(75-m)+90m≤6300,
解得m≤30.
答:最多能种植乙种花卉30平方米.
(2)该社区准备种植两种花卉共75平方米且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
12. (2021抚顺铁岭21题12分)某市公交公司为落实“绿色出行,低碳环保”的城市发展理念,计划购买A,B两种型号的新型公交车.已知购买1辆A型公交车和2辆B型公交车需要165万元,2辆A型公交车和3辆B型公交车需要270万元.
(1)求A型公交车和B型公交车每辆各多少万元?
解:(1)设A型公交车每辆x万元,B型公交车每辆y万元,根据题意得
,
解得 ,
答:A型公交车每辆45万元,B型公交车每辆60万元;
(2)公交公司计划购买A型公交车和B型公交车共140辆,且购买A型公交车的总费用不高于B型公交车的总费用,那么该公司最多购买多少辆A型公交车?
(2)设该公司购买m辆A型公交车,则购买(140-m)辆B型公交车,
根据题意得45m≤60(140-m),
解得m≤80,
∴m的最大值是80,
答:该公司最多购买80辆A型公交车.
13. (2021本溪辽阳葫芦岛21题12分)某班计划购买两种毕业纪念册,已知购买1本手绘纪念册和4本图片纪念册共需135元,购买5本手绘纪念册和2本图片纪念册共需225元.
(1)求每本手绘纪念册和每本图片纪念册的价格分别为多少元?
解:(1)设每本手绘纪念册的价格为x元,每本图片纪念册的价格为y元,根据题意得 ,
解得 ,
答:每本手绘纪念册的价格为35元,每本图片纪念册的价格为25元;
(2)设购买手绘纪念册a本,则购买图片纪念册(40-a)本,根据题意得,
35a+25(40-a)≤1100,
解得a≤10.
答:最多能购买手绘纪念册10本.
(2)该班计划购买手绘纪念册和图片纪念册共40本,总费用不超过1100元,那么最多能购买手绘纪念册多少本?
14. (2023辽阳21题12分)为提高中小学生的身体素质,各校大力开展校园足球活动.某体育用品商店抓住这一商机,第一次用30000元购进A,B两种型号的足球,并很快销售完毕,共获利12200元.其进价和售价如下表:
AA B
进价(元/个) 120 200
售价(元/个) 170 280
型号
价格
(1)该体育用品商店购进A,B两种型号的足球各多少个?
解:(1)设购进A种型号的足球x个,B种型号的足球y个.根据题意列方程组,得 ,
解得 ,
答:该体育用品商店购进A种型号的足球100个,B种型号的足球90个;
(2)设第二次购进A种型号的足球a个,则购进B种型号的足球(260-a)个.根据题意,得
120a+200(260-a)≤40000.
解得a≥150.
答:最少购进A种型号的足球150个.
(2)该体育用品商店第二次准备用不超过40000元的资金再次购进A,B两种型号的足球共260个,最少购进A种型号的足球多少个?
15. (2022抚顺22题12分)为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
解:(1)设乙工程队每天能改造道路的长度是x米,则甲工程队每天能改造道路的长度是 x米,
根据题意得 ,
解得x=40,
经检验,x=40是原分式方程的解,且符合实际.
∴ x= ×40=60(米).
答:甲工程队每天能改造道路的长度是60米,乙工程队每天能改造道路的长度是40米;
(2)设安排甲队工作m天,则乙队需工作 天,根据题意得7m+5× ≤145,解得m≥10.
答:至少安排甲队工作10天.
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
一元一次不等式
的实际应用的一
般解题步骤
性质1
性质2
性质3
不等式的
基本性质
一元一次不等式的
解法及解集表示
一般步骤
解集在数轴
上的表示
一元一次不等式组
的解法及解集表示
一般步骤
解集的类型
及其表示
不等式(组)
的解法及
不等式的应用
考点精讲
【对接教材】北师:八下第二章P36~P63;
人教:七下第九章P113~P133.
不等式的基本性质
性质1:不等式两边都加(或减)同一个整式,不等号的方向不变, 即如果a>b,那么a±c____ b±c
性质2:________________________________________________ ,
即如果a>b,c>0,那么ac______ bc(或 ____ )
性质3:________________________________________________ , 即如果a>b,c<0,那么ac______bc(或 ____ )
口诀:负变正不变
>
不等式两边乘(或除以)同一个正数,不等号的方向不变
>
>
不等式两边乘(或除以)同一个负数,不等号的方向改变
<
<
一元一次不等式的解法及解集表示
一般步骤:去分母,去括号,移项,合并同类项,系数化为1(注意不等号方向是否改变)
解集 在数轴上的表示 注意事项
x”“<”用_________ ; “<”“≤”开口向____ , “>”“≥”开口向_____
x>a x≤a x≥a 空心圆圈
左
右
解集在数轴上的表示
一元一次不等式组的解法及解集表示
一般步骤:先分别解各个不等式→在数轴上表示出各不等式的解集→确定解 集的公共部分,即为不等式组的解集
解集的类型及其表示
类型(a>b) 解集 在数轴上的表示 口诀
同大取大
同小取小
大小小大 取中间
大大小小 取不了
x≥a
x>b
x≤a
x
x>a
x≤b
_________
_________
_________
_________
x≥a
x
一元一次不等式 的实际应用的一 般解题步骤
1.找:找出题目中的不等关系(正确理解表示不等关系的关键词的意义:例如:“至少” (≥)、“最多”(≤)、“不低于”(≥)、“不高于”(≤)、“不大于”(≤)、“不小于” (≥)等)
2.设:设未知数
3.列:根据不等关系,列出不等式
4.解:解不等式
5.验:取值要符合实际意义
6.答:根据题意作答
●
易错警示
1.题目中出现一些不等关系的关键词时,在设未知数时不能出现表示不等关 系的关键词;
2.要注意所取值要符合实际意义,例如:人数必为正整数,当x 表示人数, 且x≥3 时,则x 的最小值为4,即至少有4人
一元一次不等式 的实际应用的一 般解题步骤
重难点分层练
一、一元一次不等式(组)的解法及解集表示
回顾必备知识
一题多设问
例1
已知不等式组
>1①
4(x-1)≤2(x-a)②
例1题图
(1)解不等式①的解集为________;
(2)解不等式②的解集为________;
(3)若a=-3,则该不等式组的解集为________,并将解集在数轴上表示出来;
(4)若该不等式组有3个整数解,则a的取值范围为___________.
x>4
x≤2-a
4<x≤5
-6
1. (2023沈阳铁西区二模)不等式组 的整数解的个数是( )
A. 无数个 B. 3 C. 4 D. 5
x+1>0
≥2x-1
C
2. 不等式组
2(x-1)<0
3x+1≥2x
的解集在数轴上表示正确的是( )
A
二、一元一次不等式的实际应用
回顾必备知识
例2 根据题意列不等式.
(1)“7与m的和大于3”用不等式表示为________;
(2)“y的2倍与8的和不小于-3”用不等式表示为__________;
(3)“x的 与x的和不超过5”用不等式表示为___________;
(4)“a的2倍减去3的差是一个非负数”用不等式表示为________;
(5)“x的3倍与8的和比x的5倍大”,用不等式表示为___________.
7+m>3
2y+8≥-3
x+x≤5
2a-3≥0
3x+8>5x
品名 批发价(元/个) 零售价(元/个)
A种工艺品 130 160
B种工艺品 100 120
例3 某工艺品商店采购员要到厂家批发①采购A、B两种工艺品100个,②付款总额不得超过11800元,已知两种工艺品厂家的批发价和商店的零售价如下表,试解答下列问题:
提升关键能力
(1)该采购员最多可采购A种工艺品多少个?
解:(1)设采购员购进A种工艺品x个,则购进B种工艺品(100-x)个,
由题意得130x+100(100-x)≤11800,
解得x≤60,
答:采购员最多可购进A种工艺品60个;
【分层分析】(1)设采购员可采购A种工艺品x个,根据信息①可知采购B种工艺品(100-x)个,根据信息②列出不等式_________________
_______________________;
130x+100(100-x)≤11800
(2)若该商店③把100个工艺品全部以零售价售出,为使商场获得④利润不低于2585元,则最少采购A种工艺品多少个?
(2)设采购A种工艺品y个,根据信息③可知采购B种工艺品(100-y)个,根据信息④可列不等式_____________________________________.
(160-130)y+(120-100)(100-y)≥2585
(2)设采购A种工艺品y个.
则彩购B种工艺品(100-y)个,根据题意得
(160-130)y+(120-100)(100-y)≥2585,
解得y≥58.5,
∵工艺品的个数为整数,
∴y最小取59.
答:最少采购A种工艺品59个.
●
易错警示
在解答不等式的实际应用时,不等式的结果要满足实际情况(比如人数,篮球的个数等),对于不能取小数的情况,根据实际取最近的整数.
体验辽宁考法
3. 某中学团委组织七年级和八年级共60名学生参加环保活动,七年级学生平均收集15个废弃塑料瓶,八年级学生平均收集20个废弃塑料瓶,为了保证收集废弃塑料瓶总数不少于1000个,至少需要多少八年级学生参加活动?
解:设参加活动的八年级学生为x个,则参加活动的七年级学生为(60-x)个,由题意,得
20x+15(60-x)≥1000,
解得x≥20.
∴至少需要20名八年级学生参加活动.
4. (2021沈阳铁西区期中)某中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元.
(1)求每个大地球仪和每个小地球仪各多少元?
解:(1)设每个大地球仪x元,每个小地球仪y元,根据题意可得,
解得
答:每个大地球仪52元,每个小地球仪28元;
(2)设购买大地球仪a个,则购买小地球仪(30-a)个,根据题意可得:52a+28(30-a)≤980,
解得a≤5 ,
∴30-a≥24 ,
∵小地球仪的个数为整数,
∴(30-a)最小取25.
答:至少要购买25个小地球仪.
(2)该中学决定购买以上两种地球仪共30个,总费用不超过980元,那么至少要购买多少个小地球仪?
同课章节目录
