18.2 特殊四边形 复习学案 2023--2024学年人教版八年级数学下册(无答案)
文档属性
| 名称 | 18.2 特殊四边形 复习学案 2023--2024学年人教版八年级数学下册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 570.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览


文档简介
特殊平行四边形复习
教学课题 特殊平行四边形 课时计划 第( )次课
授课教师 学科 数学 授课日期和时段
上课学生 年级 初二 上课形式
阶段 基础( ) 提高(√ ) 强化( )
教学目标 掌握菱形、矩形、正方形的性质和判定 2.掌握中点连接图形的特点
重点、难点 重点:特殊四边形性质与判定的综合应用 难点:特殊四边形的综合应用
(
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
)
一、学习与应用
(
Ⅰ、知识梳理
认真阅读、理解教材,带着自己预习的疑惑认真听课学习,
复习与本次课程相关的重点知识与公式及规律
,认真听老师
讲解本次课程基本知识要点
。课堂笔记或者其它补充填在右栏。
)
知识点一:特殊四边形的判定与性质 一.平行四边形的性质与判定 二.菱形的性质与判定。 三.矩形的性质与判定 四.正方形的性质与判定。 知识点二: 有关四边形四边中点问题的知识点: (1)顺次连接任意四边形的四边中点所得的四边形是平行四边形; (2)顺次连接矩形的四边中点所得的四边形是菱形; (3)顺次连接菱形的四边中点所得的四边形是矩形; (4)顺次连接等腰梯形的四边中点所得的四边形是菱形; (5)顺次连接对角线相等的四边形四边中点所得的四边形是菱形; (6)顺次连接对角线互相垂直的四边形四边中点所得的四边形是矩形; (7)顺次连接对角线互相垂直且相等的四边形四边中点所得的四边形是正方形; (
Ⅱ
、
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
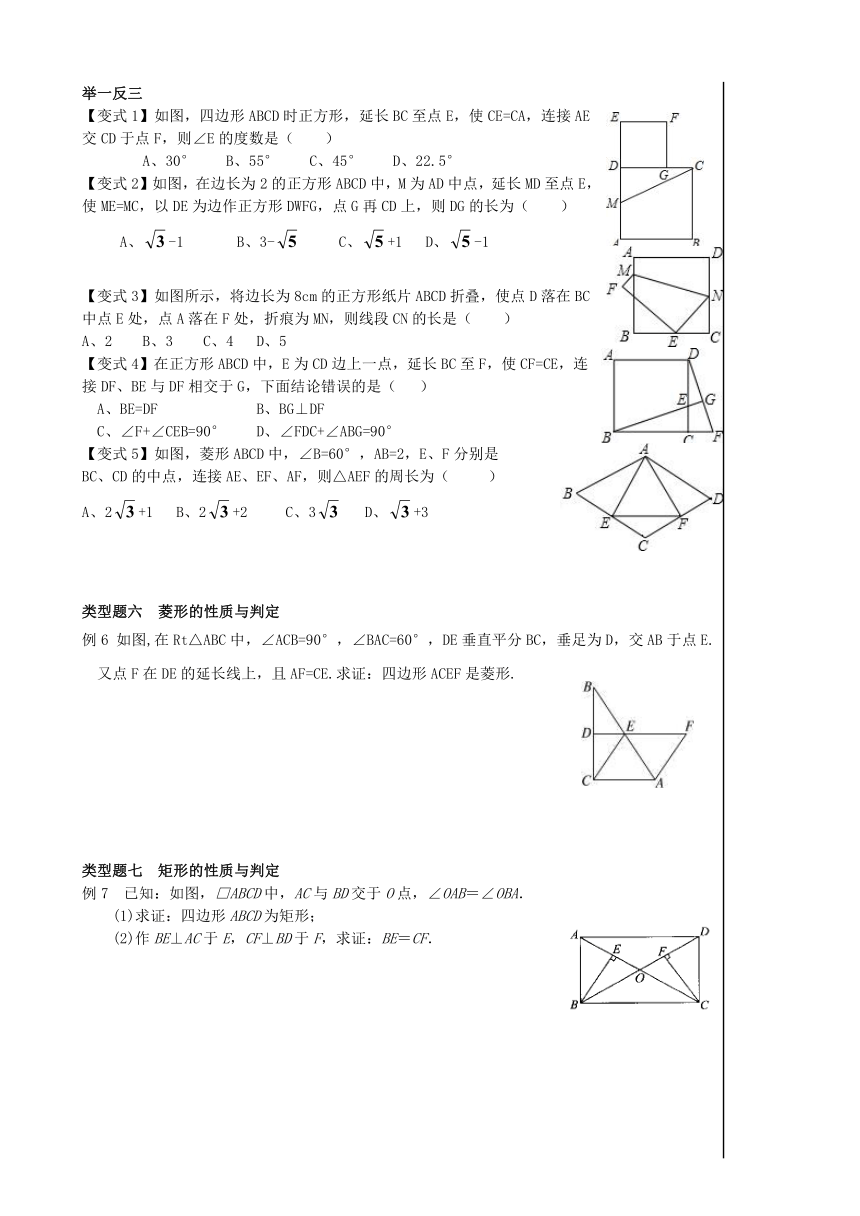
) 类型一、判断命题正确与否 例1 下列命题中正确的是( ) A、有一组邻边相等的四边形时菱形 B、有一个角是直角的平行四边形式矩形; C、对角线垂直的平行四边形是正方形 D、一组对边平行的四边形是平行四边形 举一反三: 【变式1】下列硕大正确的是( ) A、顺次连接矩形各边中点得到的四边形是矩形 B、对角线互相垂直的平行四边形时正方形 C、既是矩形又是菱形的四边形不一定是正方形 D.直角三角形斜边上的中线等于斜边的一半 【变式2】下列命题中,是真命题的是( ) A、有两边相等的四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直相等的四边形是正方形 类型题二:正方形、矩形、菱形的性质 例2 对角线互相垂直平分且相等的四边形一定是( ) A、正方形 B、菱形 C、矩形 D、平行四边形 举一反三: 【变式1】已知矩形ABCD的长为4cm,宽为3cm,则对角线AC边上的中线是( ) A、3cm B、5cm C、2.5cm D、10cm 【变式2】矩形具有而平行四边形不具有的性质是( ) A、对边相等 B、对角相等 C、对角线互相平分 D、四个角都是直角 【变式3】正方形具有而菱形不具有的性质是( ) A、对角线相等 B、四条边相等 C、对角线互相平分 D、对角线互相垂直 【变式4】菱形的一条对角线与它的边相等,则它的一个锐角等于( ) A、30° B、45° C、60° D、75° 【变式5】矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( ) A、2 B、4 C、2 D、4 类型题三:中点四边形 例3 依次连接矩形各边中点,得到的四边形是( ) A、矩形 B、菱形 C、正方形 D、梯形 举一反三 【变式1】顺次连接菱形各边中点所得的四边形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形 【变式2】顺次连接对角线相等的四边形各边中点所得的四边形时( ) A、平行四边形 B、矩形 C、菱形 D、正方形 类型题四:增加条件判定特殊四边形 例4 在平行四边形中,若增加一个条件就是矩形,增加的条件是( ) A、对角线互相平分 B、AB=BC C、AC=BD D、∠A+∠B=180° 举一反三 【变式1】下列条件中,能判定四边形时菱形,则原四边形( ) A、对角线相等 B、对角线互相垂直 C、对角线互相平分且相等 D、对角线互相垂直平分 【变式2】已知,ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形 类型题五:翻折题型、选择最后压轴题 例5 如图,已知四边形ABCD是矩形,现将△CDE沿折痕DE翻折,使点C落在点F处,若∠CED=32°,则∠ADF的大小是( ) A、26° B、27° C、28° D、25° 举一反三 【变式1】如图,四边形ABCD时正方形,延长BC至点E,使CE=CA,连接AE交CD于点F,则∠E的度数是( ) A、30° B、55° C、45° D、22.5° 【变式2】如图,在边长为2的正方形ABCD中,M为AD中点,延长MD至点E,使ME=MC,以DE为边作正方形DWFG,点G再CD上,则DG的长为( ) A、-1 B、3- C、+1 D、-1 【变式3】如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( ) A、2 B、3 C、4 D、5 【变式4】在正方形ABCD中,E为CD边上一点,延长BC至F,使CF=CE,连接DF、BE与DF相交于G,下面结论错误的是( ) A、BE=DF B、BG⊥DF C、∠F+∠CEB=90° D、∠FDC+∠ABG=90° 【变式5】如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是 BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( ) A、2+1 B、2+2 C、3 D、+3 类型题六 菱形的性质与判定 例6 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.求证:四边形ACEF是菱形. 类型题七 矩形的性质与判定 例7 已知:如图,□ABCD中,AC与BD交于O点,∠OAB=∠OBA. (1)求证:四边形ABCD为矩形; (2)作BE⊥AC于E,CF⊥BD于F,求证:BE=CF. 类型题八 方形的判定与性质 例8 已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.求证:四边形PQMN是正方形. (
Ⅲ、综合练习
-
融会贯通
将各种类型的题目融合在一起,请大家认真分析、解答下列练习,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
) 【练习1】过四边形ABCD的顶点A、B、C、D作BD、AC的平行线围成四边形EFGH,若EFGH是菱形,则四边形ABCD一定是( ) A、平行四边形 B、菱形 C、矩形 D、对角线相等的四边形 【练习2】在菱形ABCD中, 且E、F分别是BC、CD的中点,那么( ) A、 B、 C、45 D、 【练习3】矩形的一条长边的中点与另一条长边构成等腰直角三角形,已知矩形的周长是36,则矩形一条对角线长是( ) A、 B、5 C、 D、3 【练习4】矩形的内角平分线能够组成一个( ) A、矩形 B、菱形 C、正方形 D、平行四边形 【练习5】9、若两个三角形的两条中位线对应相等且两条中位线与一对应边的夹角相等,则这两个三角形的关系是( ) A、全等 B、周长相等 C、不全等 D、不确定 【练习6】正方形具有而菱形不具有的性质是( ) A、四个角都是直角 B、两组对边分别相等 C、内角和为 D、对角线平分对角 【练习7】平行四边形两邻边上的高分别为和,这两条高的夹角为,此平行四边形的周长为 ,面积为 . 【练习8】三角形三条中位线围成的三角形的周长为19,则原三角形的周长为 . 【练习9】将长为12,宽为5的矩形纸片ABCD沿对角线AC对折后,AD与BC交于点E,则DE的长度为 . 【练习10】菱形两条对角线长度比为1:,则菱形较小的内角的度数为 . (
A
B
C
D
E
F
H
G
)【练习11】ABCD为平行四边形,DFEC和BCGH为正方形.求证:. 【练习12】如图6,在矩形ABCD中,E是BC上一点且AE=AD,又于点F,证明:EC=EF. (
图
6
A
B
C
D
E
F
) 【练习15】证明:对角线相等的平行四边形是矩形; (要求:根据题意活出图形,写出已知、求证;在证明过程中,至少有两处写出推理依据)
二、总结与测评
(
Ⅳ、总结规律和方法
-
自我提升
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
)
总结升华:……
(
Ⅴ、自我反馈及课后作业测评
学完本节知识,你有哪些新收获?
总结本节的有关习题,将其中的好题及错题分类整理。
请同学们
使用错题本进行记录
。
及时检测学习效果是提高学习效果的重要保障,请同学们课后认真完成课后测评
)
课后测评
【练习1】下列命题中,真命题是 ( )
A.两条对角线垂直的四边形是菱形 B.对角线垂直且相等的四边形是正方形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
【练习2】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
【练习3】菱形具有而矩形不一定具有的性质是 ( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.对角互补
【练习4】下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有( )
A.3个 B.4个 C. 5个 D.6个
【练习5】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE。
求证:△ADE≌△CED;
求证:DE//AC;
【练习6】已知,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F,求证:四边形AEDF时菱形;
【练习7】如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE//AB交MN于E,连接AE、CD。
求证:AD=CE;
四边形ADCE的形状是 ,说明理由;
【练习8】如图,在正方形ABCD中,E,F分别为BC和CD上的点,AE和BF交于点G,现有三个关系:BE=CF,AE=BF,AE⊥BF;
从三个关系中选择一个作为条件,剩下两个作为结论,形成一个真命题,要求写出所有真命题;
选择其中一个真命题进行证明;
【练习9】已知:如图,在△ABC中,AB=AC,D为BC的中点,四边形ABDE时平行四边形。
求证:四边形ADCE时矩形;
【练习10】求证:顺次连接一个等腰梯形的各边中点,所得到的四边形是菱形.
教学课题 特殊平行四边形 课时计划 第( )次课
授课教师 学科 数学 授课日期和时段
上课学生 年级 初二 上课形式
阶段 基础( ) 提高(√ ) 强化( )
教学目标 掌握菱形、矩形、正方形的性质和判定 2.掌握中点连接图形的特点
重点、难点 重点:特殊四边形性质与判定的综合应用 难点:特殊四边形的综合应用
(
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
)
一、学习与应用
(
Ⅰ、知识梳理
认真阅读、理解教材,带着自己预习的疑惑认真听课学习,
复习与本次课程相关的重点知识与公式及规律
,认真听老师
讲解本次课程基本知识要点
。课堂笔记或者其它补充填在右栏。
)
知识点一:特殊四边形的判定与性质 一.平行四边形的性质与判定 二.菱形的性质与判定。 三.矩形的性质与判定 四.正方形的性质与判定。 知识点二: 有关四边形四边中点问题的知识点: (1)顺次连接任意四边形的四边中点所得的四边形是平行四边形; (2)顺次连接矩形的四边中点所得的四边形是菱形; (3)顺次连接菱形的四边中点所得的四边形是矩形; (4)顺次连接等腰梯形的四边中点所得的四边形是菱形; (5)顺次连接对角线相等的四边形四边中点所得的四边形是菱形; (6)顺次连接对角线互相垂直的四边形四边中点所得的四边形是矩形; (7)顺次连接对角线互相垂直且相等的四边形四边中点所得的四边形是正方形; (
Ⅱ
、
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
) 类型一、判断命题正确与否 例1 下列命题中正确的是( ) A、有一组邻边相等的四边形时菱形 B、有一个角是直角的平行四边形式矩形; C、对角线垂直的平行四边形是正方形 D、一组对边平行的四边形是平行四边形 举一反三: 【变式1】下列硕大正确的是( ) A、顺次连接矩形各边中点得到的四边形是矩形 B、对角线互相垂直的平行四边形时正方形 C、既是矩形又是菱形的四边形不一定是正方形 D.直角三角形斜边上的中线等于斜边的一半 【变式2】下列命题中,是真命题的是( ) A、有两边相等的四边形是菱形 B、有一个角是直角的四边形是矩形 C、四个角相等的菱形是正方形 D、两条对角线互相垂直相等的四边形是正方形 类型题二:正方形、矩形、菱形的性质 例2 对角线互相垂直平分且相等的四边形一定是( ) A、正方形 B、菱形 C、矩形 D、平行四边形 举一反三: 【变式1】已知矩形ABCD的长为4cm,宽为3cm,则对角线AC边上的中线是( ) A、3cm B、5cm C、2.5cm D、10cm 【变式2】矩形具有而平行四边形不具有的性质是( ) A、对边相等 B、对角相等 C、对角线互相平分 D、四个角都是直角 【变式3】正方形具有而菱形不具有的性质是( ) A、对角线相等 B、四条边相等 C、对角线互相平分 D、对角线互相垂直 【变式4】菱形的一条对角线与它的边相等,则它的一个锐角等于( ) A、30° B、45° C、60° D、75° 【变式5】矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是( ) A、2 B、4 C、2 D、4 类型题三:中点四边形 例3 依次连接矩形各边中点,得到的四边形是( ) A、矩形 B、菱形 C、正方形 D、梯形 举一反三 【变式1】顺次连接菱形各边中点所得的四边形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形 【变式2】顺次连接对角线相等的四边形各边中点所得的四边形时( ) A、平行四边形 B、矩形 C、菱形 D、正方形 类型题四:增加条件判定特殊四边形 例4 在平行四边形中,若增加一个条件就是矩形,增加的条件是( ) A、对角线互相平分 B、AB=BC C、AC=BD D、∠A+∠B=180° 举一反三 【变式1】下列条件中,能判定四边形时菱形,则原四边形( ) A、对角线相等 B、对角线互相垂直 C、对角线互相平分且相等 D、对角线互相垂直平分 【变式2】已知,ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形 类型题五:翻折题型、选择最后压轴题 例5 如图,已知四边形ABCD是矩形,现将△CDE沿折痕DE翻折,使点C落在点F处,若∠CED=32°,则∠ADF的大小是( ) A、26° B、27° C、28° D、25° 举一反三 【变式1】如图,四边形ABCD时正方形,延长BC至点E,使CE=CA,连接AE交CD于点F,则∠E的度数是( ) A、30° B、55° C、45° D、22.5° 【变式2】如图,在边长为2的正方形ABCD中,M为AD中点,延长MD至点E,使ME=MC,以DE为边作正方形DWFG,点G再CD上,则DG的长为( ) A、-1 B、3- C、+1 D、-1 【变式3】如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( ) A、2 B、3 C、4 D、5 【变式4】在正方形ABCD中,E为CD边上一点,延长BC至F,使CF=CE,连接DF、BE与DF相交于G,下面结论错误的是( ) A、BE=DF B、BG⊥DF C、∠F+∠CEB=90° D、∠FDC+∠ABG=90° 【变式5】如图,菱形ABCD中,∠B=60°,AB=2,E、F分别是 BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( ) A、2+1 B、2+2 C、3 D、+3 类型题六 菱形的性质与判定 例6 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.求证:四边形ACEF是菱形. 类型题七 矩形的性质与判定 例7 已知:如图,□ABCD中,AC与BD交于O点,∠OAB=∠OBA. (1)求证:四边形ABCD为矩形; (2)作BE⊥AC于E,CF⊥BD于F,求证:BE=CF. 类型题八 方形的判定与性质 例8 已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.求证:四边形PQMN是正方形. (
Ⅲ、综合练习
-
融会贯通
将各种类型的题目融合在一起,请大家认真分析、解答下列练习,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
) 【练习1】过四边形ABCD的顶点A、B、C、D作BD、AC的平行线围成四边形EFGH,若EFGH是菱形,则四边形ABCD一定是( ) A、平行四边形 B、菱形 C、矩形 D、对角线相等的四边形 【练习2】在菱形ABCD中, 且E、F分别是BC、CD的中点,那么( ) A、 B、 C、45 D、 【练习3】矩形的一条长边的中点与另一条长边构成等腰直角三角形,已知矩形的周长是36,则矩形一条对角线长是( ) A、 B、5 C、 D、3 【练习4】矩形的内角平分线能够组成一个( ) A、矩形 B、菱形 C、正方形 D、平行四边形 【练习5】9、若两个三角形的两条中位线对应相等且两条中位线与一对应边的夹角相等,则这两个三角形的关系是( ) A、全等 B、周长相等 C、不全等 D、不确定 【练习6】正方形具有而菱形不具有的性质是( ) A、四个角都是直角 B、两组对边分别相等 C、内角和为 D、对角线平分对角 【练习7】平行四边形两邻边上的高分别为和,这两条高的夹角为,此平行四边形的周长为 ,面积为 . 【练习8】三角形三条中位线围成的三角形的周长为19,则原三角形的周长为 . 【练习9】将长为12,宽为5的矩形纸片ABCD沿对角线AC对折后,AD与BC交于点E,则DE的长度为 . 【练习10】菱形两条对角线长度比为1:,则菱形较小的内角的度数为 . (
A
B
C
D
E
F
H
G
)【练习11】ABCD为平行四边形,DFEC和BCGH为正方形.求证:. 【练习12】如图6,在矩形ABCD中,E是BC上一点且AE=AD,又于点F,证明:EC=EF. (
图
6
A
B
C
D
E
F
) 【练习15】证明:对角线相等的平行四边形是矩形; (要求:根据题意活出图形,写出已知、求证;在证明过程中,至少有两处写出推理依据)
二、总结与测评
(
Ⅳ、总结规律和方法
-
自我提升
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
)
总结升华:……
(
Ⅴ、自我反馈及课后作业测评
学完本节知识,你有哪些新收获?
总结本节的有关习题,将其中的好题及错题分类整理。
请同学们
使用错题本进行记录
。
及时检测学习效果是提高学习效果的重要保障,请同学们课后认真完成课后测评
)
课后测评
【练习1】下列命题中,真命题是 ( )
A.两条对角线垂直的四边形是菱形 B.对角线垂直且相等的四边形是正方形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
【练习2】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
【练习3】菱形具有而矩形不一定具有的性质是 ( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.对角互补
【练习4】下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有( )
A.3个 B.4个 C. 5个 D.6个
【练习5】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE。
求证:△ADE≌△CED;
求证:DE//AC;
【练习6】已知,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F,求证:四边形AEDF时菱形;
【练习7】如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE//AB交MN于E,连接AE、CD。
求证:AD=CE;
四边形ADCE的形状是 ,说明理由;
【练习8】如图,在正方形ABCD中,E,F分别为BC和CD上的点,AE和BF交于点G,现有三个关系:BE=CF,AE=BF,AE⊥BF;
从三个关系中选择一个作为条件,剩下两个作为结论,形成一个真命题,要求写出所有真命题;
选择其中一个真命题进行证明;
【练习9】已知:如图,在△ABC中,AB=AC,D为BC的中点,四边形ABDE时平行四边形。
求证:四边形ADCE时矩形;
【练习10】求证:顺次连接一个等腰梯形的各边中点,所得到的四边形是菱形.
