18.2.3 正方形 学案 2023--2024学年人教版八年级数学下册(无答案)
文档属性
| 名称 | 18.2.3 正方形 学案 2023--2024学年人教版八年级数学下册(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 609.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览



文档简介
特殊平行四边形正方形
教学课题 正方形的性质与判定 课时计划 第( )次课
授课教师 学科 数学 授课日期和时段
上课学生 年级 初二 上课形式
阶段 基础( ) 提高(√ ) 强化( )
教学目标 掌握正方形的定义和性质,掌握正方形判定方法 2.掌握正方形性质与判定的综合应用
重点、难点 重点:正方形性质与判定的综合应用 难点: 正方形性质与判定的综合应用
(
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
)
一、学习与应用
(
Ⅰ、知识梳理
认真阅读、理解教材,带着自己预习的疑惑认真听课学习,
复习与本次课程相关的重点知识与公式及规律
,认真听老师
讲解本次课程基本知识要点
。课堂笔记或者其它补充填在右栏。
)
知识点:一.正方形的定义 内容叙述有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。知识详解(1)记忆要点:平行四边形+一组邻边相等+一个角是直角=正方形。 (2)如图所示,在□ABCD中,如果AB=AD,且∠BAD=90°, 则平行四边形ABCD是正方形。 (3)理解正方形的定义应把握以下两点: ①正方形的定义有三个条件: a.有一组邻边相等, b.有一个角为直角, c.是平行四边形,这三个条件必须同时具备,缺一不可。 ②正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形。特别提醒(1)既是矩形又是菱形的四边形是正方形。 (2)正方形不仅是特殊的平行四边形, 并且是特殊的矩形,又是特殊的菱形, 正方形、矩形、菱形都是特殊的平行四边形, 它们的关系如图所示。
知识点二:正方形的性质 正方形 的性质边对边平行,邻边互相垂直,四条边都相等。角四个角相等,都等于90°。对角线两条对角线互相垂直平分且相等;每条对角线平分一组对角。对称性是轴对称图形,有四条对称轴; 是中心对称图形,对称中心是对角线的交点。
要点诠释: (1)正方形的两条对角线把它分成四个全等的等腰直角三角形;解决有关正方形的问题时,通常归结到这些等腰直角三角形中求解。 (2)正方形的对角线也互相垂直,因此正方形的面积也可以用对角线长乘积的一半来计算。 知识点三:正方形的判定 判定说明用正方形的定义判定先判定一个四边形是平行四边形,再判定这个平行四边形是菱形(或矩形),最后判定这个菱形(或矩形)是正方形。有一组邻边相等的矩形是正方形先判定一个四边形是矩形,再判定这个矩形是菱形。有一个角是直角的菱形是正方形先判定一个四边形是菱形,再判定这个菱形是矩形。
要点诠释:矩形和菱形的判定定理是判定正方形的基础。这三种方法还可写成: 有一个角是直角,且有一组邻边相等的平行四边形是正方形; 有一组邻边相等的矩形是正方形; 有一个角是直角的菱形是正方形。 类型一 正方形的定义 (
Ⅱ
、
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
)例1 下面四个定义中不正确的是( ) A.有一个角是直角的平行四边形叫做矩形 B.有一组邻边相等的四边形叫菱形 C.有一个角是直角且有一组邻边相等的平行四边形叫正方形 D.两腰相等的梯形叫等腰梯形 举一反三: 【变式1】如右图所示,△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB。 试说明四边形BEDF是正方形。 类型二 正方形的性质 例2:已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF. (
A
B
C
D
E
F
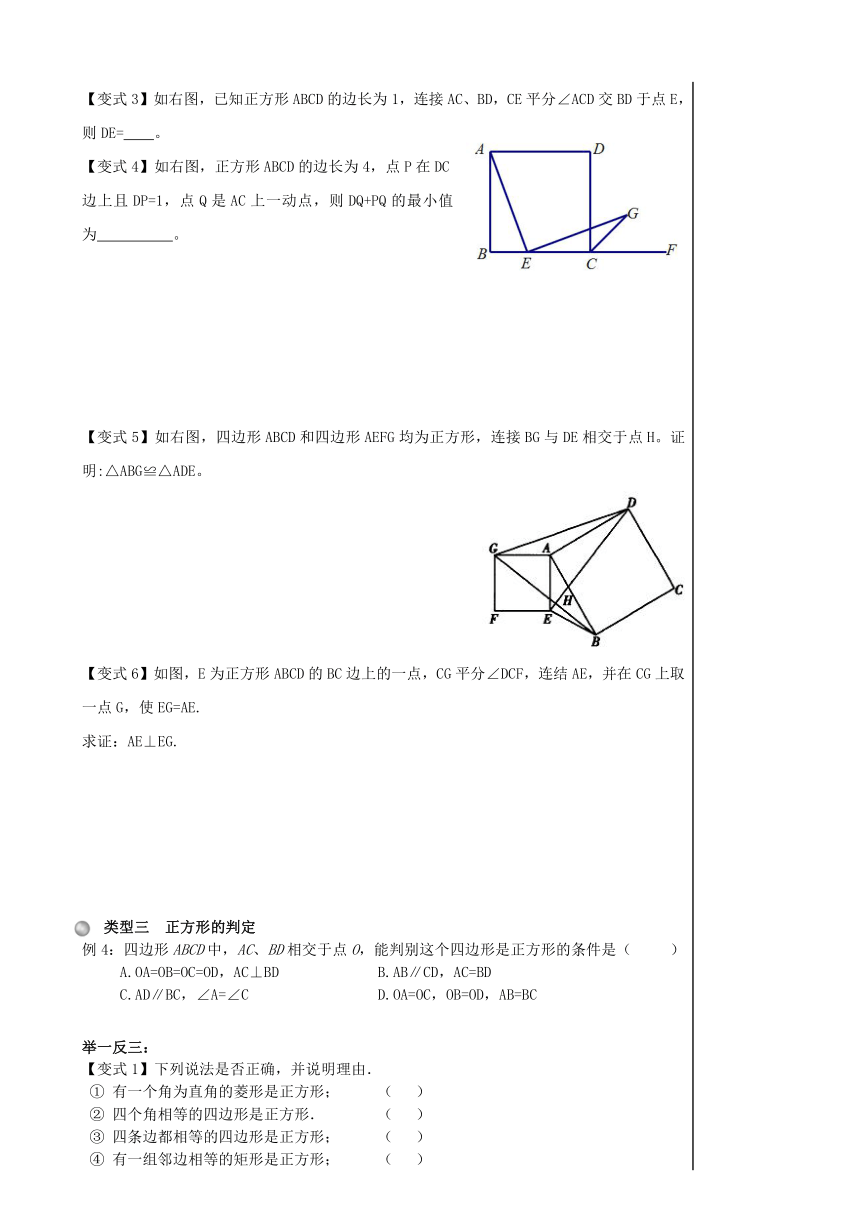
)求证:∠AFE=∠AEF. 例3:在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,求的度数。 举一反三: 【变式1】正方形具有而矩形不一定具有的特征是( ) A.四个角都相等 B.四边都相等 C.对角线相等 D.对角线互相平分 【变式2】如右图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AC于点E,BF∥DE,且交AG于点F,则下列结论不正确的是( ) A.EF=CG B.BF=AE C.AF=DE D.AF-BF=EF 变式2 变式3 变式4 【变式3】如右图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE= 。 【变式4】如右图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 。 【变式5】如右图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H。证明:△ABG≌△ADE。 【变式6】如图,E为正方形ABCD的BC边上的一点,CG平分∠DCF,连结AE,并在CG上取一点G,使EG=AE. 求证:AE⊥EG. 类型三 正方形的判定 例4:四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( ) A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC 举一反三: 【变式1】下列说法是否正确,并说明理由. ① 有一个角为直角的菱形是正方形; ( ) ② 四个角相等的四边形是正方形. ( ) ③ 四条边都相等的四边形是正方形; ( ) ④ 有一组邻边相等的矩形是正方形; ( ) ⑤ 对角线垂直且相等的四边形是正方形 ( ) ⑥ 对角线相等的菱形是正方形; ( ) ⑦ 对角线互相垂直的矩形是正方形; ( ) ⑧ 对角线互相垂直平分的四边形是正方形;( ) 【变式2】如右图,在ΔABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,四边形DECF是什么特殊的四边形 请说明理由。 【变式3】如右图,E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN, 则四边形EFMN是什么特殊的四边形?请证明你的结论。 (
Ⅲ、综合练习
-
融会贯通
将各种类型的题目融合在一起,请大家认真分析、解答下列练习,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
) 【练习1】 四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( ) A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC 【练习2】下列命题中的假命题是( ). A.一组邻边相等的平行四边形是菱形 B. 一组对边平行且相等的四边形是平行四边形 C.一组邻边相等的矩形是正方形 D.一组对边相等且有一个角是直角的四边形是矩形 【练习3】顺次连结矩形的各边中点,所得的四边形一定是( ) A.正方形 B.菱形 C.矩形 D.梯形 【练习4】如图,在ABC中∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E、F. 求证:四边形CFDE为正方形. 【练习5】如图,已知在中,,为边的中点,过点作,垂足分别为. (
A
C
D
B
F
E
)求证:; (2)若,求证:四边形是正方形.
(
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
) 二、总结与测评
(
Ⅳ、总结规律和方法
-
自我提升
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
)
总结升华:……
(
Ⅴ、自我反馈及课后作业测评
学完本节知识,你有哪些新收获?
总结本节的有关习题,将其中的好题及错题分类整理。
请同学们
使用错题本进行记录
。
及时检测学习效果是提高学习效果的重要保障,请同学们课后认真完成课后测评
)
课后测评
【练习1】下列说法错误的是( )
A、四个角相等的四边形是矩形 B、四条边相等的四边形是正方形
C、对角线相等的菱形是正方形 D、对角线互相垂直的矩形是正方形
【练习2】已知:如图,顺次连接正方形ABCD各边中点,得到四边形EFGH.求证:四边形EFGH也是正方形.
(
G
F
E
H
D
CA
B
A
)
【练习3】已知:矩形ABCD,它的四个角平分线交于E,F,G,H. 求证:四边形EFGH是正方形.
(
H
G
F
E
D
C
B
A
)
【练习3】如图所示,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F。
①当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形,请猜想并说明理由。
②在①中,当点P运动到什么位置时,矩形PEMF变为正方形?为什么?
【练习4】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
【练习4】已知Rt△ABC中,,CD平分,交AB于D,DF//BC,DE//AC,求证:四边形DECF为正方形.
【练习5】如右图,已知正方形ABDE和正方形ACFG,DM⊥BC,FN⊥BC,垂足分别为M,N试说明:BC=DM+FN。
教学课题 正方形的性质与判定 课时计划 第( )次课
授课教师 学科 数学 授课日期和时段
上课学生 年级 初二 上课形式
阶段 基础( ) 提高(√ ) 强化( )
教学目标 掌握正方形的定义和性质,掌握正方形判定方法 2.掌握正方形性质与判定的综合应用
重点、难点 重点:正方形性质与判定的综合应用 难点: 正方形性质与判定的综合应用
(
“凡事预则立,不预则废”。科学地预习才能使我们上课听讲更有目的性和针对性。
我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记。
)
一、学习与应用
(
Ⅰ、知识梳理
认真阅读、理解教材,带着自己预习的疑惑认真听课学习,
复习与本次课程相关的重点知识与公式及规律
,认真听老师
讲解本次课程基本知识要点
。课堂笔记或者其它补充填在右栏。
)
知识点:一.正方形的定义 内容叙述有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。知识详解(1)记忆要点:平行四边形+一组邻边相等+一个角是直角=正方形。 (2)如图所示,在□ABCD中,如果AB=AD,且∠BAD=90°, 则平行四边形ABCD是正方形。 (3)理解正方形的定义应把握以下两点: ①正方形的定义有三个条件: a.有一组邻边相等, b.有一个角为直角, c.是平行四边形,这三个条件必须同时具备,缺一不可。 ②正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形。特别提醒(1)既是矩形又是菱形的四边形是正方形。 (2)正方形不仅是特殊的平行四边形, 并且是特殊的矩形,又是特殊的菱形, 正方形、矩形、菱形都是特殊的平行四边形, 它们的关系如图所示。
知识点二:正方形的性质 正方形 的性质边对边平行,邻边互相垂直,四条边都相等。角四个角相等,都等于90°。对角线两条对角线互相垂直平分且相等;每条对角线平分一组对角。对称性是轴对称图形,有四条对称轴; 是中心对称图形,对称中心是对角线的交点。
要点诠释: (1)正方形的两条对角线把它分成四个全等的等腰直角三角形;解决有关正方形的问题时,通常归结到这些等腰直角三角形中求解。 (2)正方形的对角线也互相垂直,因此正方形的面积也可以用对角线长乘积的一半来计算。 知识点三:正方形的判定 判定说明用正方形的定义判定先判定一个四边形是平行四边形,再判定这个平行四边形是菱形(或矩形),最后判定这个菱形(或矩形)是正方形。有一组邻边相等的矩形是正方形先判定一个四边形是矩形,再判定这个矩形是菱形。有一个角是直角的菱形是正方形先判定一个四边形是菱形,再判定这个菱形是矩形。
要点诠释:矩形和菱形的判定定理是判定正方形的基础。这三种方法还可写成: 有一个角是直角,且有一组邻边相等的平行四边形是正方形; 有一组邻边相等的矩形是正方形; 有一个角是直角的菱形是正方形。 类型一 正方形的定义 (
Ⅱ
、
经典例题-自主学习
认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
)例1 下面四个定义中不正确的是( ) A.有一个角是直角的平行四边形叫做矩形 B.有一组邻边相等的四边形叫菱形 C.有一个角是直角且有一组邻边相等的平行四边形叫正方形 D.两腰相等的梯形叫等腰梯形 举一反三: 【变式1】如右图所示,△ABC中,∠ABC=90°,BD平分∠ABC,DE⊥BC,DF⊥AB。 试说明四边形BEDF是正方形。 类型二 正方形的性质 例2:已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF. (
A
B
C
D
E
F
)求证:∠AFE=∠AEF. 例3:在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,求的度数。 举一反三: 【变式1】正方形具有而矩形不一定具有的特征是( ) A.四个角都相等 B.四边都相等 C.对角线相等 D.对角线互相平分 【变式2】如右图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AC于点E,BF∥DE,且交AG于点F,则下列结论不正确的是( ) A.EF=CG B.BF=AE C.AF=DE D.AF-BF=EF 变式2 变式3 变式4 【变式3】如右图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE= 。 【变式4】如右图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 。 【变式5】如右图,四边形ABCD和四边形AEFG均为正方形,连接BG与DE相交于点H。证明:△ABG≌△ADE。 【变式6】如图,E为正方形ABCD的BC边上的一点,CG平分∠DCF,连结AE,并在CG上取一点G,使EG=AE. 求证:AE⊥EG. 类型三 正方形的判定 例4:四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( ) A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC 举一反三: 【变式1】下列说法是否正确,并说明理由. ① 有一个角为直角的菱形是正方形; ( ) ② 四个角相等的四边形是正方形. ( ) ③ 四条边都相等的四边形是正方形; ( ) ④ 有一组邻边相等的矩形是正方形; ( ) ⑤ 对角线垂直且相等的四边形是正方形 ( ) ⑥ 对角线相等的菱形是正方形; ( ) ⑦ 对角线互相垂直的矩形是正方形; ( ) ⑧ 对角线互相垂直平分的四边形是正方形;( ) 【变式2】如右图,在ΔABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,四边形DECF是什么特殊的四边形 请说明理由。 【变式3】如右图,E、F、M、N分别是正方形ABCD四条边上的点,且AE=BF=CM=DN, 则四边形EFMN是什么特殊的四边形?请证明你的结论。 (
Ⅲ、综合练习
-
融会贯通
将各种类型的题目融合在一起,请大家认真分析、解答下列练习,尝试总结提升各类型题目的规律和技巧,然后完成举一反三
。若有其它补充可填在右栏空白处。
) 【练习1】 四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( ) A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC 【练习2】下列命题中的假命题是( ). A.一组邻边相等的平行四边形是菱形 B. 一组对边平行且相等的四边形是平行四边形 C.一组邻边相等的矩形是正方形 D.一组对边相等且有一个角是直角的四边形是矩形 【练习3】顺次连结矩形的各边中点,所得的四边形一定是( ) A.正方形 B.菱形 C.矩形 D.梯形 【练习4】如图,在ABC中∠ACB=90°,CD平分∠ACB,DE⊥BC,DF⊥AC,垂足分别为E、F. 求证:四边形CFDE为正方形. 【练习5】如图,已知在中,,为边的中点,过点作,垂足分别为. (
A
C
D
B
F
E
)求证:; (2)若,求证:四边形是正方形.
(
要想学习成绩好,总结测评少不了!课后复习是学习不可或缺的环节,它可以帮助我们巩固学习效果,弥补知识缺漏,提高学习能力.
) 二、总结与测评
(
Ⅳ、总结规律和方法
-
自我提升
认真回顾总结本部分内容的规律和方法,熟练掌握技能技巧。
)
总结升华:……
(
Ⅴ、自我反馈及课后作业测评
学完本节知识,你有哪些新收获?
总结本节的有关习题,将其中的好题及错题分类整理。
请同学们
使用错题本进行记录
。
及时检测学习效果是提高学习效果的重要保障,请同学们课后认真完成课后测评
)
课后测评
【练习1】下列说法错误的是( )
A、四个角相等的四边形是矩形 B、四条边相等的四边形是正方形
C、对角线相等的菱形是正方形 D、对角线互相垂直的矩形是正方形
【练习2】已知:如图,顺次连接正方形ABCD各边中点,得到四边形EFGH.求证:四边形EFGH也是正方形.
(
G
F
E
H
D
CA
B
A
)
【练习3】已知:矩形ABCD,它的四个角平分线交于E,F,G,H. 求证:四边形EFGH是正方形.
(
H
G
F
E
D
C
B
A
)
【练习3】如图所示,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F。
①当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形,请猜想并说明理由。
②在①中,当点P运动到什么位置时,矩形PEMF变为正方形?为什么?
【练习4】如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:CE=CF;
(2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由.
【练习4】已知Rt△ABC中,,CD平分,交AB于D,DF//BC,DE//AC,求证:四边形DECF为正方形.
【练习5】如右图,已知正方形ABDE和正方形ACFG,DM⊥BC,FN⊥BC,垂足分别为M,N试说明:BC=DM+FN。
