西师大版六年级下册数学3.5反比例的意义课件(共23张PPT)
文档属性
| 名称 | 西师大版六年级下册数学3.5反比例的意义课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
西师大版 数学 六年级 下册
反比例的意义
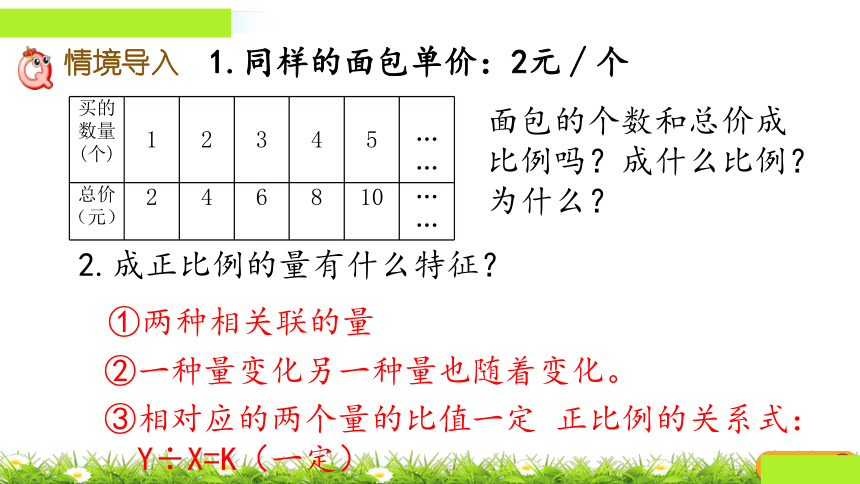
1.同样的面包单价:2元∕个
情境导入
买的数量(个) 1 2 3 4 5
……
总价(元) 2 4 6 8 10 ……
面包的个数和总价成
比例吗?成什么比例?
为什么?
2.成正比例的量有什么特征?
①两种相关联的量
②一种量变化另一种量也随着变化。
③相对应的两个量的比值一定 正比例的关系式:
Y÷X=K(一定)
2.共有30个苹果分给小朋友
情境导入
人数 1 3 5 10 ……
每个人分的个数 30 10 6 3
……
小朋友的人数和每个人分的个数成正比例吗?为什么?这两种量到底是什么关系呢?
学习目标
1.通过丰富的实例,能认识反比例。
2.通过练习能根据反比例的意义,能判断两个相关联的量是不是成反比例。
3.通过利用反比例解决一些简单的生活问题,能感受反比例关系在生活中的广泛应用。
出示目标
活动要求
1.学生独立完成表格,说说算法。
2.从表格中发现了什么规律?
活动规则
1.说清楚算法的理由。+2分
2.有补充质疑。 +1分
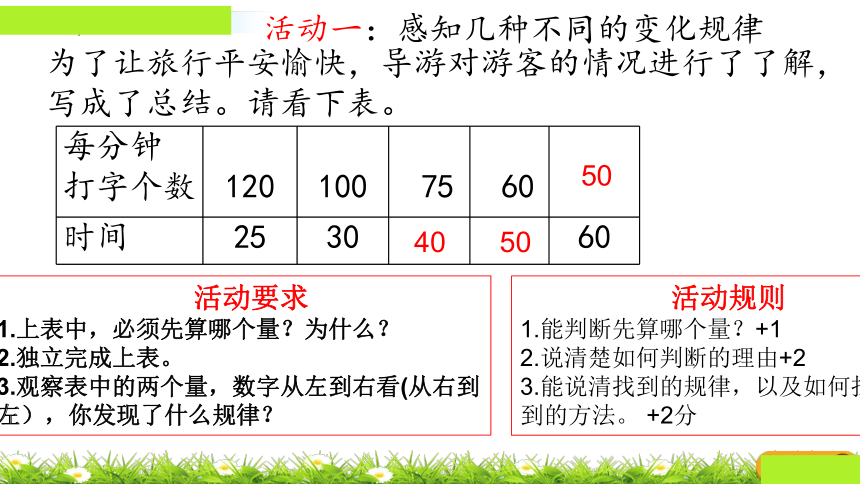
活动一:感知几种不同的变化规律
60名游客在井冈山游览,准备分组活动。
每组 人数 3 5 6 10
组数 20 12 10 4
每分钟 打字个数 120 100 75 60
时间 25 30 60
为了让旅行平安愉快,导游对游客的情况进行了了解,
写成了总结。请看下表。
活动要求
1.上表中,必须先算哪个量?为什么?
2.独立完成上表。
3.观察表中的两个量,数字从左到右看(从右到左),你发现了什么规律?
活动规则
1.能判断先算哪个量?+1
2.说清楚如何判断的理由+2
3.能说清找到的规律,以及如何找到的方法。 +2分
活动一:感知几种不同的变化规律
40
50
50
2.共有30个苹果分给小朋友
情境导入
人数 1 3 5 10 ……
每个人分的个数 30 10 6 3
……
小朋友的人数和每个人分的个数成正比例吗?为什么?这两种量到底是什么关系呢?
巩固练习:
1. 课堂活动1题。
2. 李叔叔骑车从家到工厂(同一条路),他骑车的速度和时间成不成反比例,说说理由。
3.说说生活中成反比例的量。
课堂小结
这节课你们都学会了哪些知识?
相关联的量
方向相反 反比例的量
Xy=k(一定)乘积一定
课本:
第46页第6、7、8题
课后作业
1.从教材课后习题中选取;
2.从课时练中选取。
谢谢指导!
2020春使用
反 比 例 的 应 用
六年级下册第三单元
判一判,下面的量成什么比例?
(1)总价一定,单价和数量。
(2)我们班学生做操,每行学生人数和行数。
(3)路程一定,速度和时间。
水费一定,每吨水的价钱和吨数
学习目标
1.通过运用反比例知识和多种策略,能解决生活中简单的实际问题。
2.经历探索反比例应用的学习过程,体会反比例知识和生活的联系。
“青年突击队”参加泥石流抢险,原计划每时行6km,要4小时才能到达目的地。出发时接到紧急通知要求3时到达,他们平均每时需要行多少千米?
活动要求
(1)题中有哪两个相关联的量?它们成什么关系?你是怎么判断的?
(2)尝试解决问题并说出列式依据。
活动规则
1.正确找到相关联的量+1分
2.说清如何判断他们成什么关系
+2分
3.能说清列式的依据
+1分
课堂探索
解:设他们平均每小时行x km。
3x = 6×4
x =24÷3
x =8
答:他们每小时行8km。
你还有其他做法吗?
一辆汽车从甲地开往乙地,每小时行70km,5小时到达。如果每小时行驶87.5km,需要多少小时到达?
解:需要x小时到达。
87.5x = 70×5
x =350÷87.5
x =4
答:需要4小时到达。
用同样的地板砖铺地, 铺9m2要25块,如果铺45m2要多少块
解:如果铺45m2要X 块。
9:25=45:x
9x = 25×45
x =125
答:如果铺45m2要5块。
修一条路,原计划每天修400m,25天完成。实际前4天修200m,照这样的速度,修完要用多少天?
解:修完要用x天。
(200÷4)x = 400×25
x =10000÷50
x =200
答:修完需要200天。
课堂总结
用反比例解决问题的步骤是什么?
1.设要求的问题为X;
2.判断题中哪两种量成反比例;
3.列比例式;
4.解比例,作答。
课堂总结
用比例解决问题的步骤是什么?
(1)题中有哪些变化的量和不变的量?
(2)这三种量成什么关系?
(3)列出关系等式。
通过这节课的学习,你学到了什么?
课堂总结
西师大版 数学 六年级 下册
反比例的意义
1.同样的面包单价:2元∕个
情境导入
买的数量(个) 1 2 3 4 5
……
总价(元) 2 4 6 8 10 ……
面包的个数和总价成
比例吗?成什么比例?
为什么?
2.成正比例的量有什么特征?
①两种相关联的量
②一种量变化另一种量也随着变化。
③相对应的两个量的比值一定 正比例的关系式:
Y÷X=K(一定)
2.共有30个苹果分给小朋友
情境导入
人数 1 3 5 10 ……
每个人分的个数 30 10 6 3
……
小朋友的人数和每个人分的个数成正比例吗?为什么?这两种量到底是什么关系呢?
学习目标
1.通过丰富的实例,能认识反比例。
2.通过练习能根据反比例的意义,能判断两个相关联的量是不是成反比例。
3.通过利用反比例解决一些简单的生活问题,能感受反比例关系在生活中的广泛应用。
出示目标
活动要求
1.学生独立完成表格,说说算法。
2.从表格中发现了什么规律?
活动规则
1.说清楚算法的理由。+2分
2.有补充质疑。 +1分
活动一:感知几种不同的变化规律
60名游客在井冈山游览,准备分组活动。
每组 人数 3 5 6 10
组数 20 12 10 4
每分钟 打字个数 120 100 75 60
时间 25 30 60
为了让旅行平安愉快,导游对游客的情况进行了了解,
写成了总结。请看下表。
活动要求
1.上表中,必须先算哪个量?为什么?
2.独立完成上表。
3.观察表中的两个量,数字从左到右看(从右到左),你发现了什么规律?
活动规则
1.能判断先算哪个量?+1
2.说清楚如何判断的理由+2
3.能说清找到的规律,以及如何找到的方法。 +2分
活动一:感知几种不同的变化规律
40
50
50
2.共有30个苹果分给小朋友
情境导入
人数 1 3 5 10 ……
每个人分的个数 30 10 6 3
……
小朋友的人数和每个人分的个数成正比例吗?为什么?这两种量到底是什么关系呢?
巩固练习:
1. 课堂活动1题。
2. 李叔叔骑车从家到工厂(同一条路),他骑车的速度和时间成不成反比例,说说理由。
3.说说生活中成反比例的量。
课堂小结
这节课你们都学会了哪些知识?
相关联的量
方向相反 反比例的量
Xy=k(一定)乘积一定
课本:
第46页第6、7、8题
课后作业
1.从教材课后习题中选取;
2.从课时练中选取。
谢谢指导!
2020春使用
反 比 例 的 应 用
六年级下册第三单元
判一判,下面的量成什么比例?
(1)总价一定,单价和数量。
(2)我们班学生做操,每行学生人数和行数。
(3)路程一定,速度和时间。
水费一定,每吨水的价钱和吨数
学习目标
1.通过运用反比例知识和多种策略,能解决生活中简单的实际问题。
2.经历探索反比例应用的学习过程,体会反比例知识和生活的联系。
“青年突击队”参加泥石流抢险,原计划每时行6km,要4小时才能到达目的地。出发时接到紧急通知要求3时到达,他们平均每时需要行多少千米?
活动要求
(1)题中有哪两个相关联的量?它们成什么关系?你是怎么判断的?
(2)尝试解决问题并说出列式依据。
活动规则
1.正确找到相关联的量+1分
2.说清如何判断他们成什么关系
+2分
3.能说清列式的依据
+1分
课堂探索
解:设他们平均每小时行x km。
3x = 6×4
x =24÷3
x =8
答:他们每小时行8km。
你还有其他做法吗?
一辆汽车从甲地开往乙地,每小时行70km,5小时到达。如果每小时行驶87.5km,需要多少小时到达?
解:需要x小时到达。
87.5x = 70×5
x =350÷87.5
x =4
答:需要4小时到达。
用同样的地板砖铺地, 铺9m2要25块,如果铺45m2要多少块
解:如果铺45m2要X 块。
9:25=45:x
9x = 25×45
x =125
答:如果铺45m2要5块。
修一条路,原计划每天修400m,25天完成。实际前4天修200m,照这样的速度,修完要用多少天?
解:修完要用x天。
(200÷4)x = 400×25
x =10000÷50
x =200
答:修完需要200天。
课堂总结
用反比例解决问题的步骤是什么?
1.设要求的问题为X;
2.判断题中哪两种量成反比例;
3.列比例式;
4.解比例,作答。
课堂总结
用比例解决问题的步骤是什么?
(1)题中有哪些变化的量和不变的量?
(2)这三种量成什么关系?
(3)列出关系等式。
通过这节课的学习,你学到了什么?
课堂总结
