第三单元《圆》 复习试题 2023--2024学年北师大版九年级数学下册(含答案)
文档属性
| 名称 | 第三单元《圆》 复习试题 2023--2024学年北师大版九年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 531.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-15 19:04:44 | ||
图片预览

文档简介
北师大版数学九年级下第三单元《圆》复习试题
一.选择题(共10小题)
1.如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )
A.18° B.36° C.72° D.144°
2.如图,⊙O中,点C为弦AB的中点,连接OC,OA=5,OC=3,则AB的值为( )
A.4 B.6 C.8 D.10
3.如图,在⊙O中,E是直径AB延长线上一点,CE切⊙O于点E,若CE=2BE,则∠E的余弦值为( )
A. B. C. D.
4.如图,AD是⊙O的直径,弦AB∥CD,若∠A=28°,则∠AOC的度数为( )
A.28° B.50° C.56° D.90°
5.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠D=30°,OD=4,则AC等于( )
A.6 B.4 C. D.3
6.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等 C.相等的圆心角所对的弦也相等D.相等的弦所对的圆心角也相等
7.如图,点A,B,C,D在⊙O上,连接AB、DB、CB、CD,AB⊥BC,BC=8,∠BDC=30°,则AB的长为( )
A. B. C.8 D.4
8.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm B.15cm C.10cm D.随直线MN的变化而变化
9.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是( )
A. B. C. D.
10.如图,已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连接AD,BE相交于点F,若CE=6,CD=5,则EF的长为( )
A. B. C. D.
二.填空题(共8小题)
11.已知⊙O的半径为13,弦AB=10,则⊙O上到弦AB所在直线的距离为1的点有 个.
12.已知扇形的圆心角为80°,半径为3cm,则这个扇形的面积是 cm2.
13.如图,在⊙O中,OA⊥BC,∠ADB=30°,,则OC= .
14.如图,直线AB,CD相交于点O,∠AOD=30°,半径为2cm的⊙P的圆心在直线AB上,且位于点O左侧10cm处.若⊙P以2cm/s的速度由A向B的方向移动,则 s后,⊙P与直线CD相切.
15.如图,⊙C过原点,且分别与两坐标轴交于点A,B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为 .
16.如图,扇形AOB中,∠AOB=90°,点C,D分别在OA,上,连接BC,CD,点D,O关于直线BC对称,的长为π,则图中阴影部分的面积为 .
17.如图,在⊙O的内接四边形ABCD中,AB=AC=10,,AC⊥BD,垂足为E,则DE的长为 .
18.如图,PA是⊙O的切线,A是切点,PB经过圆心O,且与⊙O交于点B,C,若AP=AB=3,则直径BC的长为 .
三.解答题(共10小题)
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,∠C=30°,求⊙O的直径.
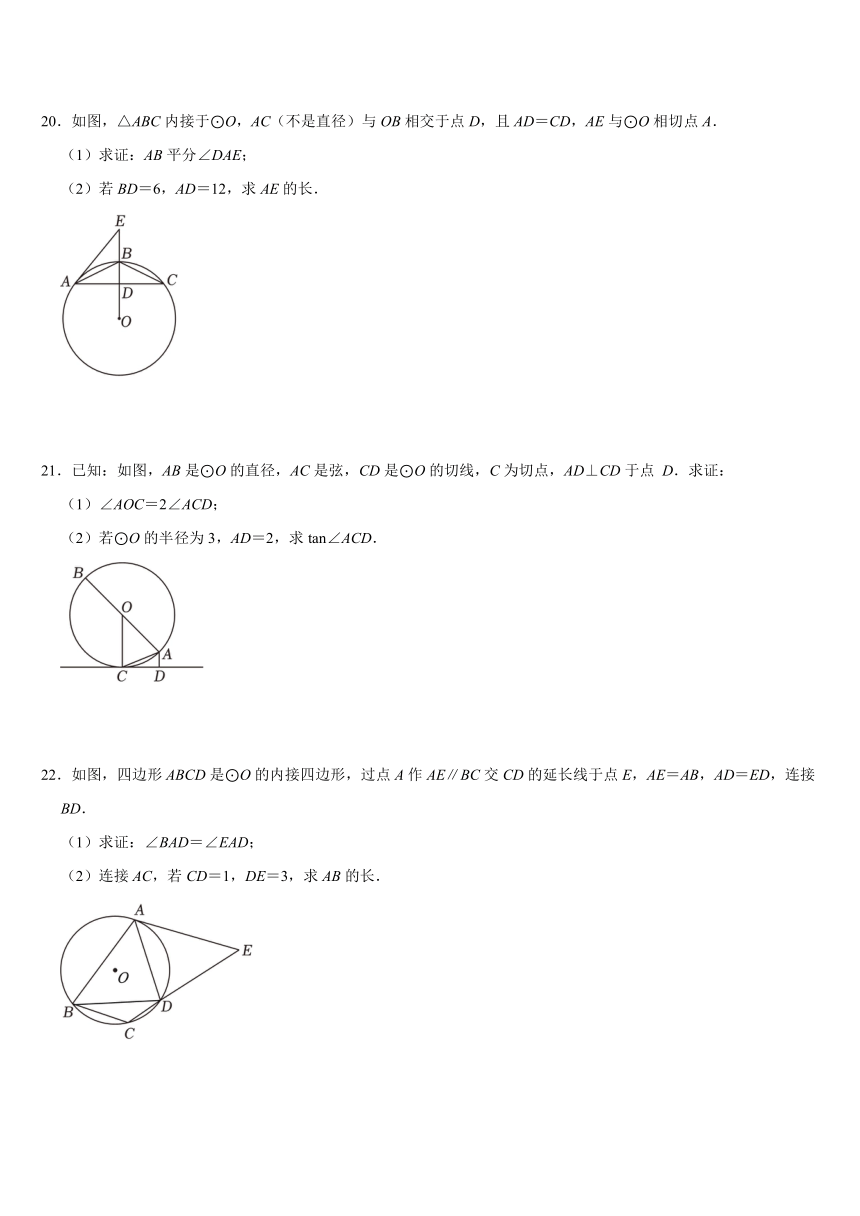
20.如图,△ABC内接于⊙O,AC(不是直径)与OB相交于点D,且AD=CD,AE与⊙O相切点A.
(1)求证:AB平分∠DAE;
(2)若BD=6,AD=12,求AE的长.
21.已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点 D.求证:
(1)∠AOC=2∠ACD;
(2)若⊙O的半径为3,AD=2,求tan∠ACD.
22.如图,四边形ABCD是⊙O的内接四边形,过点A作AE∥BC交CD的延长线于点E,AE=AB,AD=ED,连接BD.
(1)求证:∠BAD=∠EAD;
(2)连接AC,若CD=1,DE=3,求AB的长.
23.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与边AC交于点E,过点D作AC的垂线,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AE=3,EF=1,求⊙O的半径及sin∠ABC的值.
24.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)求证:∠DBC=∠DCE;
(2)若AB=8,sinD=,求BE的长.
25.如图,在Rt△ABC中,∠ACB=90°,O是BC上的一点,以点O为圆心,OC的长为半径作⊙O,且AB与⊙O相切于点H,连接AO.
(1)求证:AO平分∠BAC.
(2)若AB=5,tan∠OAC=,求⊙O的半径.
26.如图,⊙O的半径为2,四边形ABCD内接于⊙O,∠C=60°,AB=AD,连接OB,OD,延长OD至点M,使得DM=OD,连接AM.
(1)求证:四边形ABOD为菱形.
(2)判断AM与⊙O的位置关系,并说明理由.
27.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点E在上,过E作⊙O的切线,交AB的延长线于点F,若∠BEF=∠CAE.
(1)求证:AE平分∠BAC;
(2)若BF=10,EF=20,求AC的长.
28.已知:如图,⊙O的直径AB垂直于弦CD,过点C的切线与直径AB的延长线相交于点P,连接PD.
(1)求证:PD是⊙O的切线.
(2)若PD=4,tan∠DAB=,求直径AB的长.
参考答案
一.选择题(共10小题)
1.C.
2.C.
3.B.
4.C.
5.C.
6.B.
7.A.
8.A.
9.B.
10.A.
二.填空题(共8小题)
11.3.
12.2π.
13.2.
14.3或7.
15.3.
16..
17.3.
18.2.
三.解答题(共10小题)
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,∠C=30°,求⊙O的直径.
(1)证明:∵∠P=∠C,
而∠1=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)解:连接OC,如图,
∵∠1=30°,
∴∠P=30°,
∵CD⊥AB,
∴=,
∴∠BOC=2∠P=60°,
∴△BOC为等边三角形,
∴OB=BC=3,
∴⊙O的直径为6.
20.如图,△ABC内接于⊙O,AC(不是直径)与OB相交于点D,且AD=CD,AE与⊙O相切点A.
(1)求证:AB平分∠DAE;
(2)若BD=6,AD=12,求AE的长.
(1)证明:连接OA,则OA=OB,
∴∠OAB=∠OBA,
∵AE与⊙O相切于点A,
∴AE⊥OA,
∴∠EAO=90°,
∵AD=CD,
∴OB⊥AD,
∴∠ADB=90°,
∴∠DAB+∠OBA=90°,
∵∠EAB+∠OAB=∠EAO=90°,
∴∠EAB=∠DAB,
∴AB平分∠DAE.
(2)解:∵∠ADO=90°,
∴AD2+OD2=OA2,
∵BD=6,AD=12,
∴OD=OB﹣6=OA﹣6,
∴122+(OA﹣6)2=OA2,
解得OA=15,
∴OD=15﹣6=9,
∴tan∠AOE===,
∴AE=OA=×15=20,
∴AE的长为20.
21.已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点 D.求证:
(1)∠AOC=2∠ACD;
(2)若⊙O的半径为3,AD=2,求tan∠ACD.
(1)证明:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠OAC=90°,
∵CD是⊙O的切线,
∴∠OCD=90°,
即∠OCA+∠DCA=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠ABC=∠ACD,
∴∠AOC=2∠ABC=2∠ACD;
(2)解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ABC=∠ACD,
∴△ABC∽△ACD,
∴,
∴,
解得,
在Rt△ACD中,CD==2,
∴在Rt△ACD中,.
22.如图,四边形ABCD是⊙O的内接四边形,过点A作AE∥BC交CD的延长线于点E,AE=AB,AD=ED,连接BD.
(1)求证:∠BAD=∠EAD;
(2)连接AC,若CD=1,DE=3,求AB的长.
(1)证明:∵AD=ED,
∴∠EAD=∠E,
∵AE∥BC,
∴∠E+∠BCD=180°,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠EAD;
(2)解:如图,连接AC,
在△ADB和△ADE中,
,
∴△ADB≌△ADE(SAS),
∴∠ABD=∠E,
由圆周角定理得:∠ABD=∠ACD,
∴∠ACD=∠E=∠EAD,
∵∠E=∠E,
∴△ACE∽△DAE,
∴=,即=,
解得:AE=2,
∴AB=AE=2.
23.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与边AC交于点E,过点D作AC的垂线,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AE=3,EF=1,求⊙O的半径及sin∠ABC的值.
(1)证明:∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∵OD是⊙O的半径,
∴DF为⊙O的切线;
(2)解:连接DE,AD,
∵四边形ABDE是圆内接四边形,
∴∠ABC+AED=180°,
∵∠DEF+∠AED=180°,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∴DE=DC,
∴△DEC是等腰三角形,
又∵DF⊥EF,
∴DF是△DEC的中线,
∴EF=FC=1,AF=4,
∴AC=AF+CF=5,
∴AB=5,
∴⊙O的半径为2.5;
∵AB为⊙O的直径,
∴∠ADB=90°=∠ADC,
∴∠DAF=90°﹣∠ADF=∠FDC,
∴△ADF∽△DCF,
∴=,
∴DF2=AF CF=4×1=4,
∴DF=2,
在Rt△ADF中,
AD==2,
∴sinC==,
∴sin∠ABC=.
答:⊙O的半径为2.5,sin∠ABC的值是.
24.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)求证:∠DBC=∠DCE;
(2)若AB=8,sinD=,求BE的长.
(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCE=90°,
∵BD与⊙O相切于点B,
∴BD⊥AB,
∴∠ABD=90°,
∴∠DBC=∠A=90°﹣∠ABC,
∵OA=OC,
∴∠A=∠OCA,
∵∠DCE=∠OCA,
∴∠DBC=∠DCE.
(2)解:∵AB=8,
∴OC=OB=AB=4,
∵=sinD=,
∴OD=OB=×4=6,
∴DC=OD﹣OC=6﹣4=2,DB===2,
∵∠DBC=∠DCE,∠D=∠D,
∴△DBC∽△DCE,
∴=,
∴DE===,
∴BE=DB﹣DE=2﹣=,
∴BE的长是.
25.如图,在Rt△ABC中,∠ACB=90°,O是BC上的一点,以点O为圆心,OC的长为半径作⊙O,且AB与⊙O相切于点H,连接AO.
(1)求证:AO平分∠BAC.
(2)若AB=5,tan∠OAC=,求⊙O的半径.
(1)证明:连接OH,
∵AB与圆相切于H,
∴OH⊥AB,
∵∠ACB=90°,
∴OC⊥AC,
∵OC=OH,
∴AO平分∠BAC;
(2)解:设⊙O的半径是r,
∵tan∠CAO==,
∴AC=2OC=2r,
∵半径OC⊥AC,
∴AC切圆于C,
∵AH切圆于H,
∴AH=AC=2r,
∴BH=AB﹣AH=5﹣r,
∵tanB==,
∴=,
∴BC=10﹣4r,
∵AB2=AC2+BC2,
∴(2r)2+(10﹣4r)2=52,
∴4r2﹣16r+15=0,
∴r=1.5或r=2.5(bu不符合题意,舍去),
∴⊙O的半径是1.5.
26.如图,⊙O的半径为2,四边形ABCD内接于⊙O,∠C=60°,AB=AD,连接OB,OD,延长OD至点M,使得DM=OD,连接AM.
(1)求证:四边形ABOD为菱形.
(2)判断AM与⊙O的位置关系,并说明理由.
(1)证明:如图,连接OA.
∵∠C=60°,
∴∠BOD=120°.
又∵AB=AD,
∴∠AOB=∠AOD=60°.
又∵OA=OD,
∴△AOD为等边三角形,
∴AD=OD.
∵AB=AD,OB=OD,
∴AB=AD=OB=OD,
∴四边形ABOD为菱形.
(2)解:AM与⊙O相切.
理由:∵△AOD为等边三角形,
∴∠ADO=∠OAD=60°,
∴∠ADM=120°.
又∵OD=DM,OD=AD,
∴DM=AD,
∴∠DAM=30°,
∴∠OAM=90°,
∴AM与⊙O相切.
27.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点E在上,过E作⊙O的切线,交AB的延长线于点F,若∠BEF=∠CAE.
(1)求证:AE平分∠BAC;
(2)若BF=10,EF=20,求AC的长.
(1)证明:连接OE,交BC于点G,
∵EF与⊙O相切于点E,
∴∠OEF=90°,
∴∠BEF+∠OEB=90°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠OBE=90°,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠BEF=∠EAB,
∵∠BEF=∠CAE,
∴∠CAE=∠EAB,
∴AE平分∠BAC;
(2)解:∵AB是⊙O的直径,
∴∠C=90°,
∵OA=OE,
∴∠BAE=∠AEO,
∵∠CAE=∠EAB,
∴∠CAE=∠AEO,
∴AC∥OE,
∴∠C=∠OGB=90°,
∴CG=BG,
∵OA=OB,
∴OG是△ACB的中位线,
∴AC=2OG,
∵∠F=∠F,∠BEF=∠BAE,
∴△FEB∽△FAE,
∴=,
∴=,
∴AF=40,
∴AB=AF﹣BF=40﹣10=30,
∴OA=OB=OE=AB=15,
∵∠OGB=∠OEF=90°,
∴BC∥EF,
∴=,
∴=,
解得:OG=9,
∴AC=2OG=18,
∴AC的长为18.
28.已知:如图,⊙O的直径AB垂直于弦CD,过点C的切线与直径AB的延长线相交于点P,连接PD.
(1)求证:PD是⊙O的切线.
(2)若PD=4,tan∠DAB=,求直径AB的长.
(1)证明:连接OD,OC,
∵PC是⊙O的切线,
∴∠PCO=90°,
∵AB⊥CD,AB是直径,
∴=,
∴∠DOP=∠COP,
在△DOP和△COP中,
,
∴△DOP≌△COP(SAS),
∴∠PDO=∠PCO=90°,
∵D在⊙O上,
∴PD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠PDO=90°,
∴∠ADO=∠PDB=90°﹣∠BDO,
∵OA=OD,
∴∠A=∠ADO,
∴∠A=∠PDB,
∵∠BPD=∠BPD,
∴△PDB∽△PAD,
∴==,
∵tan∠DAB==,
∴==,
∵PD=4,
∴PB=2,PA=8,
∴AB=8﹣2=6.
一.选择题(共10小题)
1.如图,点A、B、C在⊙O上,∠OBC=18°,则∠A=( )
A.18° B.36° C.72° D.144°
2.如图,⊙O中,点C为弦AB的中点,连接OC,OA=5,OC=3,则AB的值为( )
A.4 B.6 C.8 D.10
3.如图,在⊙O中,E是直径AB延长线上一点,CE切⊙O于点E,若CE=2BE,则∠E的余弦值为( )
A. B. C. D.
4.如图,AD是⊙O的直径,弦AB∥CD,若∠A=28°,则∠AOC的度数为( )
A.28° B.50° C.56° D.90°
5.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠D=30°,OD=4,则AC等于( )
A.6 B.4 C. D.3
6.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等 C.相等的圆心角所对的弦也相等D.相等的弦所对的圆心角也相等
7.如图,点A,B,C,D在⊙O上,连接AB、DB、CB、CD,AB⊥BC,BC=8,∠BDC=30°,则AB的长为( )
A. B. C.8 D.4
8.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm,小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为( )
A.20cm B.15cm C.10cm D.随直线MN的变化而变化
9.如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,∠ACO=120°,AB=4,则圆心点D的坐标是( )
A. B. C. D.
10.如图,已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连接AD,BE相交于点F,若CE=6,CD=5,则EF的长为( )
A. B. C. D.
二.填空题(共8小题)
11.已知⊙O的半径为13,弦AB=10,则⊙O上到弦AB所在直线的距离为1的点有 个.
12.已知扇形的圆心角为80°,半径为3cm,则这个扇形的面积是 cm2.
13.如图,在⊙O中,OA⊥BC,∠ADB=30°,,则OC= .
14.如图,直线AB,CD相交于点O,∠AOD=30°,半径为2cm的⊙P的圆心在直线AB上,且位于点O左侧10cm处.若⊙P以2cm/s的速度由A向B的方向移动,则 s后,⊙P与直线CD相切.
15.如图,⊙C过原点,且分别与两坐标轴交于点A,B,点A的坐标为(0,3),M是第三象限内⊙C上一点,∠BMO=120°,则⊙C的半径为 .
16.如图,扇形AOB中,∠AOB=90°,点C,D分别在OA,上,连接BC,CD,点D,O关于直线BC对称,的长为π,则图中阴影部分的面积为 .
17.如图,在⊙O的内接四边形ABCD中,AB=AC=10,,AC⊥BD,垂足为E,则DE的长为 .
18.如图,PA是⊙O的切线,A是切点,PB经过圆心O,且与⊙O交于点B,C,若AP=AB=3,则直径BC的长为 .
三.解答题(共10小题)
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,∠C=30°,求⊙O的直径.
20.如图,△ABC内接于⊙O,AC(不是直径)与OB相交于点D,且AD=CD,AE与⊙O相切点A.
(1)求证:AB平分∠DAE;
(2)若BD=6,AD=12,求AE的长.
21.已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点 D.求证:
(1)∠AOC=2∠ACD;
(2)若⊙O的半径为3,AD=2,求tan∠ACD.
22.如图,四边形ABCD是⊙O的内接四边形,过点A作AE∥BC交CD的延长线于点E,AE=AB,AD=ED,连接BD.
(1)求证:∠BAD=∠EAD;
(2)连接AC,若CD=1,DE=3,求AB的长.
23.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与边AC交于点E,过点D作AC的垂线,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AE=3,EF=1,求⊙O的半径及sin∠ABC的值.
24.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)求证:∠DBC=∠DCE;
(2)若AB=8,sinD=,求BE的长.
25.如图,在Rt△ABC中,∠ACB=90°,O是BC上的一点,以点O为圆心,OC的长为半径作⊙O,且AB与⊙O相切于点H,连接AO.
(1)求证:AO平分∠BAC.
(2)若AB=5,tan∠OAC=,求⊙O的半径.
26.如图,⊙O的半径为2,四边形ABCD内接于⊙O,∠C=60°,AB=AD,连接OB,OD,延长OD至点M,使得DM=OD,连接AM.
(1)求证:四边形ABOD为菱形.
(2)判断AM与⊙O的位置关系,并说明理由.
27.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点E在上,过E作⊙O的切线,交AB的延长线于点F,若∠BEF=∠CAE.
(1)求证:AE平分∠BAC;
(2)若BF=10,EF=20,求AC的长.
28.已知:如图,⊙O的直径AB垂直于弦CD,过点C的切线与直径AB的延长线相交于点P,连接PD.
(1)求证:PD是⊙O的切线.
(2)若PD=4,tan∠DAB=,求直径AB的长.
参考答案
一.选择题(共10小题)
1.C.
2.C.
3.B.
4.C.
5.C.
6.B.
7.A.
8.A.
9.B.
10.A.
二.填空题(共8小题)
11.3.
12.2π.
13.2.
14.3或7.
15.3.
16..
17.3.
18.2.
三.解答题(共10小题)
19.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,∠C=30°,求⊙O的直径.
(1)证明:∵∠P=∠C,
而∠1=∠C,
∴∠1=∠P,
∴CB∥PD;
(2)解:连接OC,如图,
∵∠1=30°,
∴∠P=30°,
∵CD⊥AB,
∴=,
∴∠BOC=2∠P=60°,
∴△BOC为等边三角形,
∴OB=BC=3,
∴⊙O的直径为6.
20.如图,△ABC内接于⊙O,AC(不是直径)与OB相交于点D,且AD=CD,AE与⊙O相切点A.
(1)求证:AB平分∠DAE;
(2)若BD=6,AD=12,求AE的长.
(1)证明:连接OA,则OA=OB,
∴∠OAB=∠OBA,
∵AE与⊙O相切于点A,
∴AE⊥OA,
∴∠EAO=90°,
∵AD=CD,
∴OB⊥AD,
∴∠ADB=90°,
∴∠DAB+∠OBA=90°,
∵∠EAB+∠OAB=∠EAO=90°,
∴∠EAB=∠DAB,
∴AB平分∠DAE.
(2)解:∵∠ADO=90°,
∴AD2+OD2=OA2,
∵BD=6,AD=12,
∴OD=OB﹣6=OA﹣6,
∴122+(OA﹣6)2=OA2,
解得OA=15,
∴OD=15﹣6=9,
∴tan∠AOE===,
∴AE=OA=×15=20,
∴AE的长为20.
21.已知:如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点 D.求证:
(1)∠AOC=2∠ACD;
(2)若⊙O的半径为3,AD=2,求tan∠ACD.
(1)证明:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠OAC=90°,
∵CD是⊙O的切线,
∴∠OCD=90°,
即∠OCA+∠DCA=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠ABC=∠ACD,
∴∠AOC=2∠ABC=2∠ACD;
(2)解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ABC=∠ACD,
∴△ABC∽△ACD,
∴,
∴,
解得,
在Rt△ACD中,CD==2,
∴在Rt△ACD中,.
22.如图,四边形ABCD是⊙O的内接四边形,过点A作AE∥BC交CD的延长线于点E,AE=AB,AD=ED,连接BD.
(1)求证:∠BAD=∠EAD;
(2)连接AC,若CD=1,DE=3,求AB的长.
(1)证明:∵AD=ED,
∴∠EAD=∠E,
∵AE∥BC,
∴∠E+∠BCD=180°,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠EAD;
(2)解:如图,连接AC,
在△ADB和△ADE中,
,
∴△ADB≌△ADE(SAS),
∴∠ABD=∠E,
由圆周角定理得:∠ABD=∠ACD,
∴∠ACD=∠E=∠EAD,
∵∠E=∠E,
∴△ACE∽△DAE,
∴=,即=,
解得:AE=2,
∴AB=AE=2.
23.如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与边AC交于点E,过点D作AC的垂线,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若AE=3,EF=1,求⊙O的半径及sin∠ABC的值.
(1)证明:∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∵OD是⊙O的半径,
∴DF为⊙O的切线;
(2)解:连接DE,AD,
∵四边形ABDE是圆内接四边形,
∴∠ABC+AED=180°,
∵∠DEF+∠AED=180°,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∴DE=DC,
∴△DEC是等腰三角形,
又∵DF⊥EF,
∴DF是△DEC的中线,
∴EF=FC=1,AF=4,
∴AC=AF+CF=5,
∴AB=5,
∴⊙O的半径为2.5;
∵AB为⊙O的直径,
∴∠ADB=90°=∠ADC,
∴∠DAF=90°﹣∠ADF=∠FDC,
∴△ADF∽△DCF,
∴=,
∴DF2=AF CF=4×1=4,
∴DF=2,
在Rt△ADF中,
AD==2,
∴sinC==,
∴sin∠ABC=.
答:⊙O的半径为2.5,sin∠ABC的值是.
24.如图,AB为⊙O的直径,点C为圆周上一点,OC的延长线交⊙O的切线BD于点D,AC的延长线交⊙O的切线BD于点E.
(1)求证:∠DBC=∠DCE;
(2)若AB=8,sinD=,求BE的长.
(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCE=90°,
∵BD与⊙O相切于点B,
∴BD⊥AB,
∴∠ABD=90°,
∴∠DBC=∠A=90°﹣∠ABC,
∵OA=OC,
∴∠A=∠OCA,
∵∠DCE=∠OCA,
∴∠DBC=∠DCE.
(2)解:∵AB=8,
∴OC=OB=AB=4,
∵=sinD=,
∴OD=OB=×4=6,
∴DC=OD﹣OC=6﹣4=2,DB===2,
∵∠DBC=∠DCE,∠D=∠D,
∴△DBC∽△DCE,
∴=,
∴DE===,
∴BE=DB﹣DE=2﹣=,
∴BE的长是.
25.如图,在Rt△ABC中,∠ACB=90°,O是BC上的一点,以点O为圆心,OC的长为半径作⊙O,且AB与⊙O相切于点H,连接AO.
(1)求证:AO平分∠BAC.
(2)若AB=5,tan∠OAC=,求⊙O的半径.
(1)证明:连接OH,
∵AB与圆相切于H,
∴OH⊥AB,
∵∠ACB=90°,
∴OC⊥AC,
∵OC=OH,
∴AO平分∠BAC;
(2)解:设⊙O的半径是r,
∵tan∠CAO==,
∴AC=2OC=2r,
∵半径OC⊥AC,
∴AC切圆于C,
∵AH切圆于H,
∴AH=AC=2r,
∴BH=AB﹣AH=5﹣r,
∵tanB==,
∴=,
∴BC=10﹣4r,
∵AB2=AC2+BC2,
∴(2r)2+(10﹣4r)2=52,
∴4r2﹣16r+15=0,
∴r=1.5或r=2.5(bu不符合题意,舍去),
∴⊙O的半径是1.5.
26.如图,⊙O的半径为2,四边形ABCD内接于⊙O,∠C=60°,AB=AD,连接OB,OD,延长OD至点M,使得DM=OD,连接AM.
(1)求证:四边形ABOD为菱形.
(2)判断AM与⊙O的位置关系,并说明理由.
(1)证明:如图,连接OA.
∵∠C=60°,
∴∠BOD=120°.
又∵AB=AD,
∴∠AOB=∠AOD=60°.
又∵OA=OD,
∴△AOD为等边三角形,
∴AD=OD.
∵AB=AD,OB=OD,
∴AB=AD=OB=OD,
∴四边形ABOD为菱形.
(2)解:AM与⊙O相切.
理由:∵△AOD为等边三角形,
∴∠ADO=∠OAD=60°,
∴∠ADM=120°.
又∵OD=DM,OD=AD,
∴DM=AD,
∴∠DAM=30°,
∴∠OAM=90°,
∴AM与⊙O相切.
27.如图,已知△ABC内接于⊙O,AB是⊙O的直径,点E在上,过E作⊙O的切线,交AB的延长线于点F,若∠BEF=∠CAE.
(1)求证:AE平分∠BAC;
(2)若BF=10,EF=20,求AC的长.
(1)证明:连接OE,交BC于点G,
∵EF与⊙O相切于点E,
∴∠OEF=90°,
∴∠BEF+∠OEB=90°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠OBE=90°,
∵OE=OB,
∴∠OEB=∠OBE,
∴∠BEF=∠EAB,
∵∠BEF=∠CAE,
∴∠CAE=∠EAB,
∴AE平分∠BAC;
(2)解:∵AB是⊙O的直径,
∴∠C=90°,
∵OA=OE,
∴∠BAE=∠AEO,
∵∠CAE=∠EAB,
∴∠CAE=∠AEO,
∴AC∥OE,
∴∠C=∠OGB=90°,
∴CG=BG,
∵OA=OB,
∴OG是△ACB的中位线,
∴AC=2OG,
∵∠F=∠F,∠BEF=∠BAE,
∴△FEB∽△FAE,
∴=,
∴=,
∴AF=40,
∴AB=AF﹣BF=40﹣10=30,
∴OA=OB=OE=AB=15,
∵∠OGB=∠OEF=90°,
∴BC∥EF,
∴=,
∴=,
解得:OG=9,
∴AC=2OG=18,
∴AC的长为18.
28.已知:如图,⊙O的直径AB垂直于弦CD,过点C的切线与直径AB的延长线相交于点P,连接PD.
(1)求证:PD是⊙O的切线.
(2)若PD=4,tan∠DAB=,求直径AB的长.
(1)证明:连接OD,OC,
∵PC是⊙O的切线,
∴∠PCO=90°,
∵AB⊥CD,AB是直径,
∴=,
∴∠DOP=∠COP,
在△DOP和△COP中,
,
∴△DOP≌△COP(SAS),
∴∠PDO=∠PCO=90°,
∵D在⊙O上,
∴PD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠PDO=90°,
∴∠ADO=∠PDB=90°﹣∠BDO,
∵OA=OD,
∴∠A=∠ADO,
∴∠A=∠PDB,
∵∠BPD=∠BPD,
∴△PDB∽△PAD,
∴==,
∵tan∠DAB==,
∴==,
∵PD=4,
∴PB=2,PA=8,
∴AB=8﹣2=6.
