第1-4单元能力提升卷-数学五年级下册北师大版(含答案)
文档属性
| 名称 | 第1-4单元能力提升卷-数学五年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 482.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 08:19:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第1-4单元能力提升卷-数学五年级下册北师大版
一、选择题
1.下列算式( )的结果在和之间。
A.× B.×
C.× D.×
2.将下图沿虚线折起来,可折成一个小正方体。这个小正方体1号面的对面是( )号面。
A.2 B.6 C.4 D.5
3.一台拖拉机每小时耕地公顷,则3台每小时可以耕地( )公顷。
A. B. C. D.
4.棱长为2米的正方体盒子中可以放( )个棱长为2分米的小正方体。
A.10 B.100 C.1000 D.2000
5.一个小正方体的棱长是大正方体的,大正方体的表面积是小正方体的( )倍。
A.4 B.8 C.16 D.64
6.一根长方体木料的长是1.2米,沿着横截面锯成3段,表面积增加24平方厘米,原来这根木料的体积是( )立方厘米。
A.480 B.28.8 C.720 D.8640
二、填空题
7.在括号里填上合适的单位。
一本数学课本的体积大约是0.3( )。
一台热水器的容积是60( )。
一个梨的体积大约是350( )。
一台冰柜的体积大约是2.4( )。
8.与和的分数单位是( ),它有( )个这样的分数单位。
9.在括号里合适的数。
吨=( )千克 ( )
900mL=( )升 时=( )分
10.一个长方体切开后表面积增加了32平方分米,正好变成两个完全一样的正方体,这个长方体原来的表面积是( ),棱长和是( )。
11.一个长方体鱼缸的容积是288L,从里面量这个鱼缸的高正好是0.6m,鱼缸的占地面积是( )m2。
12.手工课上,淘气在一块长方体(高lcm)橡皮上挖出一个棱长1cm的正方体(如下图),表面积( )(填“增加”或“减少”)了( )dm2。
三、判断题
13.a的等于,a就等于2。( )
14.正方体和长方体的体积都可以用底面积乘高来计算。( )
15.一个25寸电视机外壳的体积约是1.5立方分米。( )
16.正方体的棱长扩大2倍,则表面积和体积都扩大4倍。( )
17.因为,所以和7都是倒数。( )
四、计算题
18.直接写得数。
19.计算下面图形的表面积和体积。
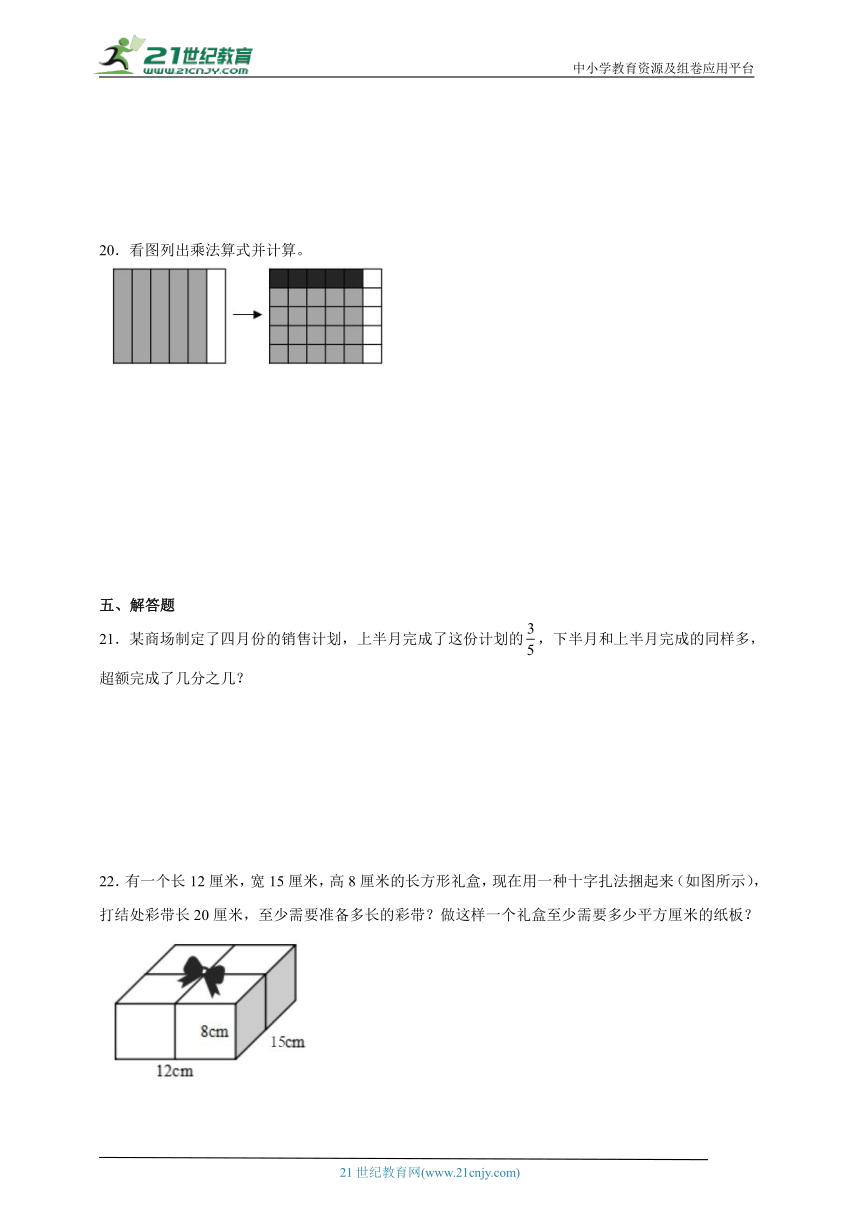
20.看图列出乘法算式并计算。
五、解答题
21.某商场制定了四月份的销售计划,上半月完成了这份计划的,下半月和上半月完成的同样多,超额完成了几分之几?
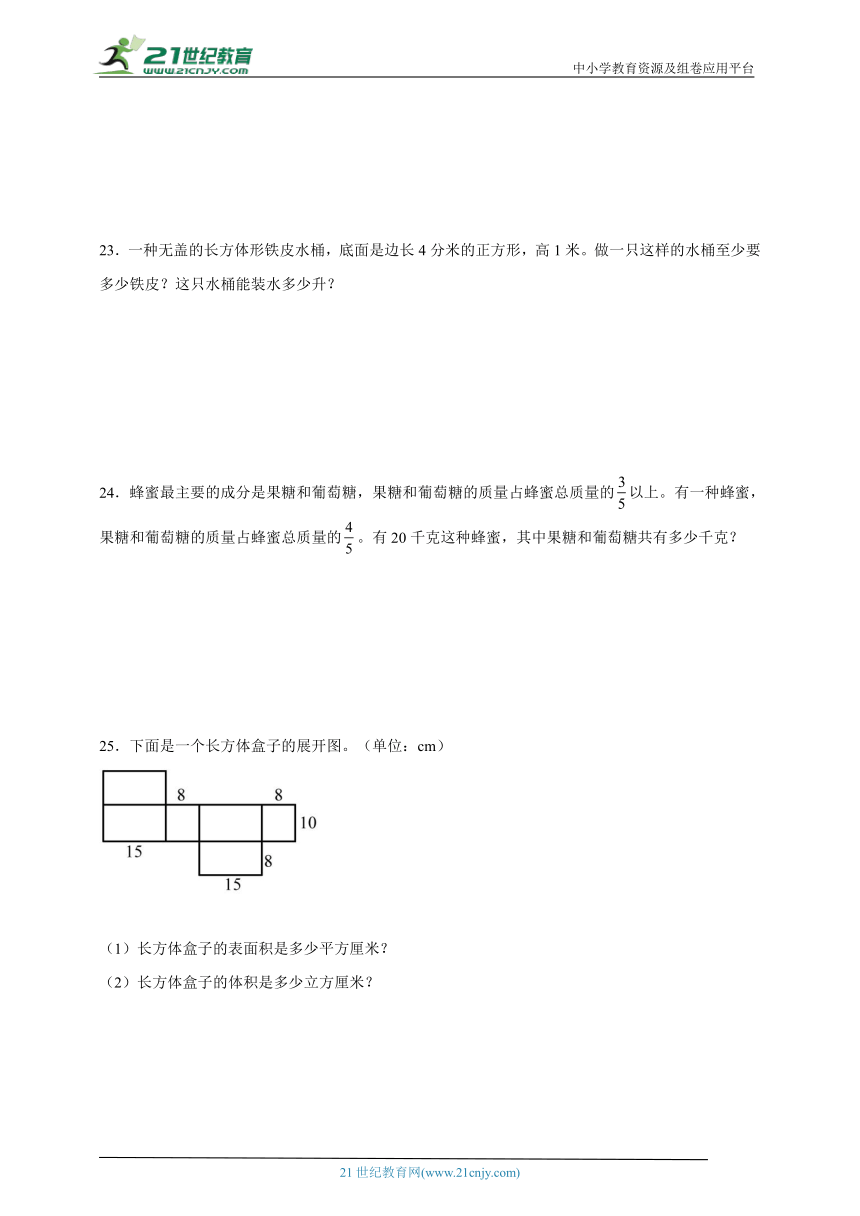
22.有一个长12厘米,宽15厘米,高8厘米的长方形礼盒,现在用一种十字扎法捆起来(如图所示),打结处彩带长20厘米,至少需要准备多长的彩带?做这样一个礼盒至少需要多少平方厘米的纸板?
23.一种无盖的长方体形铁皮水桶,底面是边长4分米的正方形,高1米。做一只这样的水桶至少要多少铁皮?这只水桶能装水多少升?
24.蜂蜜最主要的成分是果糖和葡萄糖,果糖和葡萄糖的质量占蜂蜜总质量的以上。有一种蜂蜜,果糖和葡萄糖的质量占蜂蜜总质量的。有20千克这种蜂蜜,其中果糖和葡萄糖共有多少千克?
25.下面是一个长方体盒子的展开图。(单位:cm)
(1)长方体盒子的表面积是多少平方厘米?
(2)长方体盒子的体积是多少立方厘米?
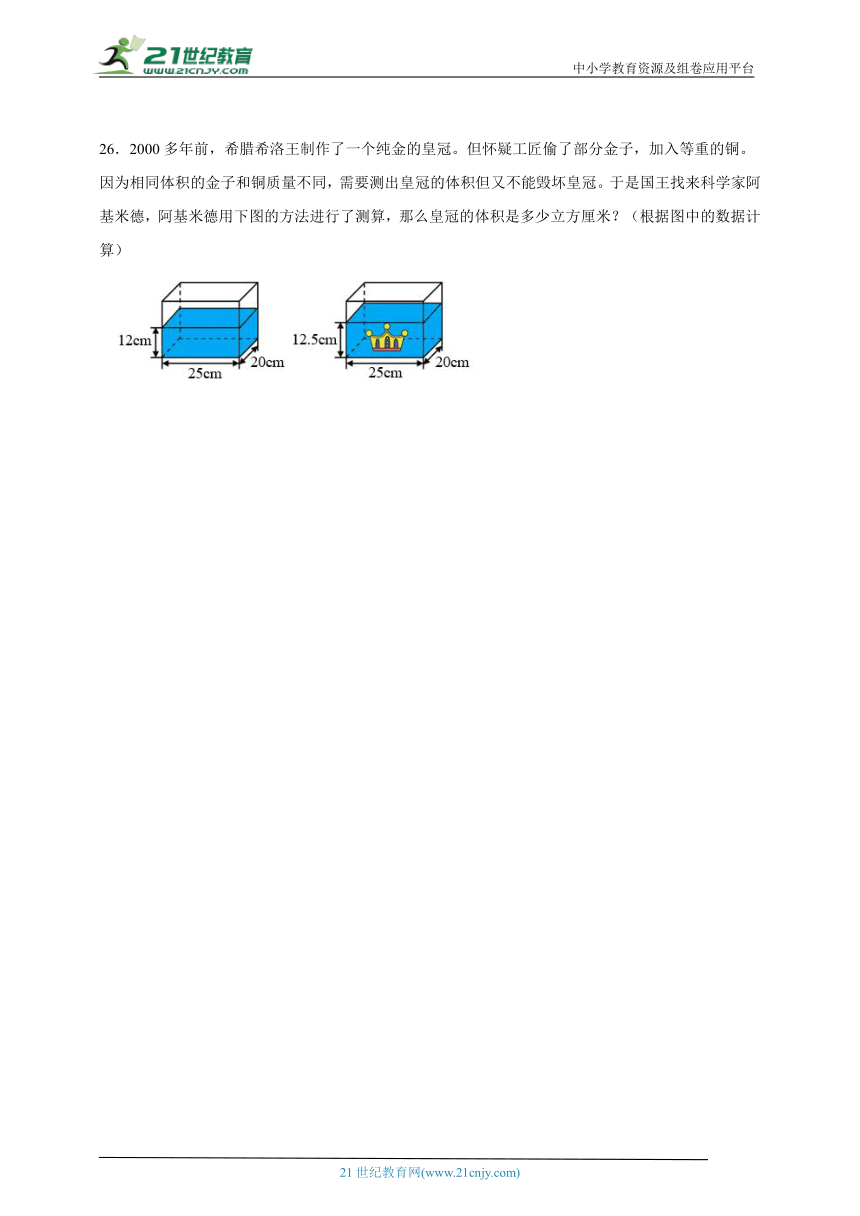
26.2000多年前,希腊希洛王制作了一个纯金的皇冠。但怀疑工匠偷了部分金子,加入等重的铜。因为相同体积的金子和铜质量不同,需要测出皇冠的体积但又不能毁坏皇冠。于是国王找来科学家阿基米德,阿基米德用下图的方法进行了测算,那么皇冠的体积是多少立方厘米?(根据图中的数据计算)
参考答案:
1.C
【分析】根据分数与分数的乘法计算法则,计算出各选择的计算结果,再进行比较,即可解答。
【详解】A.×=;<,×的结果不在和之间,不符合题意;
B.×=,<,×的结果不在和之间,不符合题意;
C.×=,<<,×的结果在和之间,符合题意;
D.×=,>,×的结果不在和之间,不符合题意。
下列算式×的结果在和之间。
故答案为:C
【点睛】熟练掌握分数与分数的乘法计算以及异分母分数比较大小的方法是解答关键。
2.D
【分析】将图沿虚线折起来,使它成为一个正方体,这个正方体1号面对的面是5号,2号面对的面是4号,3号面的对面是6。
【详解】由分析可得:这个小正方体1主要是号面的对面是5号面;
故答案为:D
【点睛】本题是考查正方体的展开图,训练学生的观察能力和空间想象能力。
3.A
【分析】一台拖拉机每小时耕地的面积×台数=耕地总面积即可求解。
【详解】由分析可知:
(公顷)
所以 3台每小时可以耕地公顷。
【点睛】本题考查分数与整数乘法应用题,解题的关键是明确一台拉机每小时耕地的面积×台数=耕地总面积。
4.C
【分析】由于1米=10分米,2米=20分米,20分米是2分米的倍数,所以正方体的盒子能够完全放下小正方体,不存在多余空间,利用正方体的体积公式:棱长×棱长×棱长,把数代入公式求出正方体盒子和小正方体的体积,再用正方体盒子的体积除以小正方体的体积即可求解。
【详解】2米=20分米
20×20×20÷(2×2×2)
=8000÷8
=1000(个)
所以棱长为2米的正方体盒子中可以放1000个棱长为2分米的小正方体。
故答案为:C
【点睛】本题主要考查正方体的体积公式,熟练掌握它的公式并灵活运用。
5.C
【分析】假设大正方体的棱长为4,则把大正方体的棱长可看作单位“1”,一个小正方体的棱长是大正方体的,根据分数乘法的意义,用4×即可求出小正方体的棱长,再根据正方体的表面积=棱长×棱长×6,代入数据求出大、小正方体的表面积,进而求出它们之间的关系。
【详解】假设大正方体的棱长为4,
4×=1
4×4×6=96
1×1×6=6
96÷6=16
一个小正方体的棱长是大正方体的,大正方体的表面积是小正方体的16倍。
故答案为:C
【点睛】本题主要考查了正方体表面积公式以及分数乘法的灵活应用。
6.C
【分析】根据题意可知,把这个长方体木料锯成3段,表面积增加了24平方厘米,表面积增加的是4个截面的面积,据此可以求出长方体木料的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.2米=120厘米
24÷4×120
=6×120
=720(立方厘米)
这根长方体木料的体积是720立方厘米。
故答案为:C
【点睛】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
7. 立方分米/dm3 升/L 立方厘米/cm3 立方米/m3
【分析】根据体积(容积)单位和数据大小的认识,结合生活实际,进行解答。
【详解】一本数学课本的体积大约是0.3立方分米
一台热水器的容积是60升
一个梨的体积大约是350立方厘米
一台冰柜的体积大约是2.4立方米
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
8. 11
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。先根据异分母分数加减法的计算方法求出与的和,进而判断出结果的分数单位,分子是几,就有几个这样的分数单位。据此解答。
【详解】+=
与和的分数单位是,它有11个这样的分数单位。
【点睛】本题考查了异分母分数的计算方法以及分数单位的认识。
9. 340 8060 0.9 36
【分析】将吨换算成千克数,用乘进率1000得340千克;将8.06m3换算成dm3数,用8.06乘进率1000得8060dm3;将900mL换算成升数,用900除以进率1000得0.9升;将时换算成分钟数,用乘进率60得36分;据此解答。
【详解】由分析可得:
吨=340千克 8.06m3=8060dm3
900mL=0.9升 时=36分
【点睛】本题主要考查单位间的换算,牢记进率是解题的关键。
10. 160平方分米/160dm2 64分米/64dm
【分析】把长方体切成两个完全一样的正方体,的表面积增加了两个正方形面,用32÷2即可求出每个面的面积,进而判断出长方体的宽和高,长方体的长是高的2倍,据此求出长方形的长,然后根据长方体表面积公式:长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,代入数据解答。
【详解】32÷2=16(平方分米)
16=4×4
2×4=8(分米)
所以长方体的宽和高为4分米,长为8分米,
(4×4+4×8+4×8)×2
=(16+32+32)×2
=80×2
=160(平方分米)
(4+4+8)×4
=16×4
=64(分米)
这个长方体原来的表面积是160平方分米,棱长和是64分米。
【点睛】本题主要考查了长方体、正方体的认识以及长方体表面积公式、长方体棱长和公式的灵活应用,要注意表面积增加了哪些面。
11.0.48
【分析】首先把288L换算成0.288m3,根据长方体的容积(体积)公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】288L=0.288m3
0.288÷0.6=0.48(m2)
鱼缸的占地面积是0.48m2。
【点睛】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式,注意:容积单位与体积之间的换算。
12. 增加 0.02
【分析】在长方体(高1cm)橡皮上挖出一个棱长1cm的正方体,长方体上下两个面比原来减少2个小正方形的面积,同时内部也增加了4个小正方形的面积,所以表面积比原来大2个小正方形的面积。
【详解】1×1×2=2(cm2)
2 cm2=0.02 dm2
所以表面积增加了0.02 dm2。
【点睛】本题考查的关键在于明确切割后的图形表面积增加或减少了哪几个面。并注意单位陷阱,是否需要单位换算。
13.×
【分析】根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】÷=×=
a等于,所以本题说法错误。
故答案为:×
【点睛】明确已知一个数的几分之几是多少,求这个数,用除法解答,是解答此题的关键。
14.√
【分析】根据正方体和长方体的体积公式判断此题,据此判断。
【详解】正方体的体积=长×宽×高=底面积×高
长方体的体积=长×宽×高=底面积×高
原题说法正确。
故答案为:√
【点睛】本题涉及的考点较多,但都属于基础题,要牢记有关知识点的概念,并熟练运用。
15.√
【分析】根据生活经验和实际情况,对体积单位和数据大小的认识,可知计量一个电视机外壳的体积用“立方分米”做单位;由此解答。
【详解】根据分析可知,一个25寸电视机外壳的体积约是1.5立方分米。
原题干说法正确。
故答案为:√
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
16.×
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可。
【详解】正方体的棱长扩大2倍,它的表面积就扩大倍。
体积扩大倍。
因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍。这种说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、因数与积的变化规律及应用。
17.×
【分析】倒数的意义:乘积是1的两个数叫做互为倒数,倒数是互相依存的,据此分析判断。
【详解】因为,所以是7的倒数,或7是的倒数,不能说和7都是倒数,所以因为,所以和7都是倒数的说法是错误的;
故答案为:×
【点睛】本题主要考查倒数的意义,注意倒数是互相依存的。
18.;;;0
;;22;
【详解】略
19.表面积:344cm2
体积:420cm3
【分析】根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】表面积:(10×7+10×6+7×6)×2
=(70+60+42)×2
=172×2
=344(cm2)
体积:10×7×6=420(cm3)
20.×=
【分析】先这个正方形的面积看作单位“1”,把它平均分成6份,其中5份涂色,是整个正方形的,再把每份平均分成5小份,每小份是的,其中1小份涂色,是整个正方形的的,根据分数乘法的意义,用乘即可。
【详解】
×==
21.
【分析】根据题意可知,把这份计划看作单位“1”,上半月完成了这份计划的,下半月和上半月完成的同样多,则下半月也完成了这份计划的,根据分数减法的意义,用+-1即可求出超额完成了几分之几。
【详解】+-1
=-1
=
答:超额完成了。
【点睛】本题考查了分数加减法的计算和混合应用。
22.106厘米;792平方厘米
【分析】根据题意可知,需要彩带总长等于2条长+2条宽+4条高+打结处彩带长20厘米,即可求出需要彩带的总长度;
求做这样一个礼盒至少需要的纸盒多少平方厘米,就是求这个礼盒的表面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】12×2+15×2+8×4+20
=24+30+32+20
=54+32+20
=86+20
=106(厘米)
(12×15+12×8+15×8)×2
=(180+96+120)×2
=(276+120)×2
=396×2
=792(平方厘米)
答:至少需要准备106厘米的彩带,做这样一个礼盒至少需要792平方厘米。
【点睛】本题主要考查长方体棱长总和与表面积公式的应用。
23.176平方分米;160升
【分析】1米=10分米,无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用4×4+4×10×2+4×10×2即可求出无盖的长方体铁皮箱的表面积。根据长方体的体积=长×宽×高,用4×4×10即可求出这只水桶的体积,再把单位换算成升。
【详解】1米=10分米
4×4+4×10×2+4×10×2
=16+80+80
=176(平方分米)
4×4×10=160(立方分米)
160立方分米=160升
答:做一只这样的水桶至少要176平方分米铁皮;这只水桶能装水160升。
【点睛】本题主要考查了长方体表面积公式和体积公式的灵活应用,关键是明确表面积有几个面。
24.16千克
【分析】根据题意,把这种蜂蜜的质量看作单位“1”,根据分数乘法的意义,用这种蜂蜜质量×,即可求出果糖和葡萄糖共有多少千克。
【详解】20×=16(千克)
答:其中果糖和葡萄糖共有16千克。
【点睛】本题考查分数乘法的应用题,解题关键是找出题目中的单位“1”是哪个量,再根据分数乘法的意义,进行列数解答。
25.(1)700平方厘米
(2)1200立方厘米
【分析】(1)根据长方体的特点,有4个长,4个宽,4个高,一般长方体的长宽高的长度不同,由此即可知道长方体的长是15厘米,宽是8厘米,高是10厘米,根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
(2)根据长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】(1)(15×8+15×10+8×10)×2
=(120+150+80)×2
=350×2
=700(平方厘米)
答:长方体盒子的表面积是700平方厘米。
(2)15×8×10
=120×10
=1200(立方厘米)
答:长方体盒子的体积是1200立方厘米。
【点睛】本题主要考查长方体的展开图以及它的表面积和体积公式,熟练掌握它们的公式并灵活运用。
26.250立方厘米
【分析】由题意可知:上升部分的水的体积等于皇冠的体积,先求出水面上升的高度,再用上升的高度×长方体的底面积即可。
【详解】(12.5-12)×(25×20)
=0.5×500
=250(立方厘米)
答:皇冠的体积是250立方厘米。
【点睛】本题主要考查不规则物体体积的计算方法,理解上升部分的水的体积等于皇冠的体积是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-4单元能力提升卷-数学五年级下册北师大版
一、选择题
1.下列算式( )的结果在和之间。
A.× B.×
C.× D.×
2.将下图沿虚线折起来,可折成一个小正方体。这个小正方体1号面的对面是( )号面。
A.2 B.6 C.4 D.5
3.一台拖拉机每小时耕地公顷,则3台每小时可以耕地( )公顷。
A. B. C. D.
4.棱长为2米的正方体盒子中可以放( )个棱长为2分米的小正方体。
A.10 B.100 C.1000 D.2000
5.一个小正方体的棱长是大正方体的,大正方体的表面积是小正方体的( )倍。
A.4 B.8 C.16 D.64
6.一根长方体木料的长是1.2米,沿着横截面锯成3段,表面积增加24平方厘米,原来这根木料的体积是( )立方厘米。
A.480 B.28.8 C.720 D.8640
二、填空题
7.在括号里填上合适的单位。
一本数学课本的体积大约是0.3( )。
一台热水器的容积是60( )。
一个梨的体积大约是350( )。
一台冰柜的体积大约是2.4( )。
8.与和的分数单位是( ),它有( )个这样的分数单位。
9.在括号里合适的数。
吨=( )千克 ( )
900mL=( )升 时=( )分
10.一个长方体切开后表面积增加了32平方分米,正好变成两个完全一样的正方体,这个长方体原来的表面积是( ),棱长和是( )。
11.一个长方体鱼缸的容积是288L,从里面量这个鱼缸的高正好是0.6m,鱼缸的占地面积是( )m2。
12.手工课上,淘气在一块长方体(高lcm)橡皮上挖出一个棱长1cm的正方体(如下图),表面积( )(填“增加”或“减少”)了( )dm2。
三、判断题
13.a的等于,a就等于2。( )
14.正方体和长方体的体积都可以用底面积乘高来计算。( )
15.一个25寸电视机外壳的体积约是1.5立方分米。( )
16.正方体的棱长扩大2倍,则表面积和体积都扩大4倍。( )
17.因为,所以和7都是倒数。( )
四、计算题
18.直接写得数。
19.计算下面图形的表面积和体积。
20.看图列出乘法算式并计算。
五、解答题
21.某商场制定了四月份的销售计划,上半月完成了这份计划的,下半月和上半月完成的同样多,超额完成了几分之几?
22.有一个长12厘米,宽15厘米,高8厘米的长方形礼盒,现在用一种十字扎法捆起来(如图所示),打结处彩带长20厘米,至少需要准备多长的彩带?做这样一个礼盒至少需要多少平方厘米的纸板?
23.一种无盖的长方体形铁皮水桶,底面是边长4分米的正方形,高1米。做一只这样的水桶至少要多少铁皮?这只水桶能装水多少升?
24.蜂蜜最主要的成分是果糖和葡萄糖,果糖和葡萄糖的质量占蜂蜜总质量的以上。有一种蜂蜜,果糖和葡萄糖的质量占蜂蜜总质量的。有20千克这种蜂蜜,其中果糖和葡萄糖共有多少千克?
25.下面是一个长方体盒子的展开图。(单位:cm)
(1)长方体盒子的表面积是多少平方厘米?
(2)长方体盒子的体积是多少立方厘米?
26.2000多年前,希腊希洛王制作了一个纯金的皇冠。但怀疑工匠偷了部分金子,加入等重的铜。因为相同体积的金子和铜质量不同,需要测出皇冠的体积但又不能毁坏皇冠。于是国王找来科学家阿基米德,阿基米德用下图的方法进行了测算,那么皇冠的体积是多少立方厘米?(根据图中的数据计算)
参考答案:
1.C
【分析】根据分数与分数的乘法计算法则,计算出各选择的计算结果,再进行比较,即可解答。
【详解】A.×=;<,×的结果不在和之间,不符合题意;
B.×=,<,×的结果不在和之间,不符合题意;
C.×=,<<,×的结果在和之间,符合题意;
D.×=,>,×的结果不在和之间,不符合题意。
下列算式×的结果在和之间。
故答案为:C
【点睛】熟练掌握分数与分数的乘法计算以及异分母分数比较大小的方法是解答关键。
2.D
【分析】将图沿虚线折起来,使它成为一个正方体,这个正方体1号面对的面是5号,2号面对的面是4号,3号面的对面是6。
【详解】由分析可得:这个小正方体1主要是号面的对面是5号面;
故答案为:D
【点睛】本题是考查正方体的展开图,训练学生的观察能力和空间想象能力。
3.A
【分析】一台拖拉机每小时耕地的面积×台数=耕地总面积即可求解。
【详解】由分析可知:
(公顷)
所以 3台每小时可以耕地公顷。
【点睛】本题考查分数与整数乘法应用题,解题的关键是明确一台拉机每小时耕地的面积×台数=耕地总面积。
4.C
【分析】由于1米=10分米,2米=20分米,20分米是2分米的倍数,所以正方体的盒子能够完全放下小正方体,不存在多余空间,利用正方体的体积公式:棱长×棱长×棱长,把数代入公式求出正方体盒子和小正方体的体积,再用正方体盒子的体积除以小正方体的体积即可求解。
【详解】2米=20分米
20×20×20÷(2×2×2)
=8000÷8
=1000(个)
所以棱长为2米的正方体盒子中可以放1000个棱长为2分米的小正方体。
故答案为:C
【点睛】本题主要考查正方体的体积公式,熟练掌握它的公式并灵活运用。
5.C
【分析】假设大正方体的棱长为4,则把大正方体的棱长可看作单位“1”,一个小正方体的棱长是大正方体的,根据分数乘法的意义,用4×即可求出小正方体的棱长,再根据正方体的表面积=棱长×棱长×6,代入数据求出大、小正方体的表面积,进而求出它们之间的关系。
【详解】假设大正方体的棱长为4,
4×=1
4×4×6=96
1×1×6=6
96÷6=16
一个小正方体的棱长是大正方体的,大正方体的表面积是小正方体的16倍。
故答案为:C
【点睛】本题主要考查了正方体表面积公式以及分数乘法的灵活应用。
6.C
【分析】根据题意可知,把这个长方体木料锯成3段,表面积增加了24平方厘米,表面积增加的是4个截面的面积,据此可以求出长方体木料的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.2米=120厘米
24÷4×120
=6×120
=720(立方厘米)
这根长方体木料的体积是720立方厘米。
故答案为:C
【点睛】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
7. 立方分米/dm3 升/L 立方厘米/cm3 立方米/m3
【分析】根据体积(容积)单位和数据大小的认识,结合生活实际,进行解答。
【详解】一本数学课本的体积大约是0.3立方分米
一台热水器的容积是60升
一个梨的体积大约是350立方厘米
一台冰柜的体积大约是2.4立方米
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
8. 11
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。先根据异分母分数加减法的计算方法求出与的和,进而判断出结果的分数单位,分子是几,就有几个这样的分数单位。据此解答。
【详解】+=
与和的分数单位是,它有11个这样的分数单位。
【点睛】本题考查了异分母分数的计算方法以及分数单位的认识。
9. 340 8060 0.9 36
【分析】将吨换算成千克数,用乘进率1000得340千克;将8.06m3换算成dm3数,用8.06乘进率1000得8060dm3;将900mL换算成升数,用900除以进率1000得0.9升;将时换算成分钟数,用乘进率60得36分;据此解答。
【详解】由分析可得:
吨=340千克 8.06m3=8060dm3
900mL=0.9升 时=36分
【点睛】本题主要考查单位间的换算,牢记进率是解题的关键。
10. 160平方分米/160dm2 64分米/64dm
【分析】把长方体切成两个完全一样的正方体,的表面积增加了两个正方形面,用32÷2即可求出每个面的面积,进而判断出长方体的宽和高,长方体的长是高的2倍,据此求出长方形的长,然后根据长方体表面积公式:长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的棱长和公式:长方体棱长和=(长+宽+高)×4,代入数据解答。
【详解】32÷2=16(平方分米)
16=4×4
2×4=8(分米)
所以长方体的宽和高为4分米,长为8分米,
(4×4+4×8+4×8)×2
=(16+32+32)×2
=80×2
=160(平方分米)
(4+4+8)×4
=16×4
=64(分米)
这个长方体原来的表面积是160平方分米,棱长和是64分米。
【点睛】本题主要考查了长方体、正方体的认识以及长方体表面积公式、长方体棱长和公式的灵活应用,要注意表面积增加了哪些面。
11.0.48
【分析】首先把288L换算成0.288m3,根据长方体的容积(体积)公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】288L=0.288m3
0.288÷0.6=0.48(m2)
鱼缸的占地面积是0.48m2。
【点睛】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式,注意:容积单位与体积之间的换算。
12. 增加 0.02
【分析】在长方体(高1cm)橡皮上挖出一个棱长1cm的正方体,长方体上下两个面比原来减少2个小正方形的面积,同时内部也增加了4个小正方形的面积,所以表面积比原来大2个小正方形的面积。
【详解】1×1×2=2(cm2)
2 cm2=0.02 dm2
所以表面积增加了0.02 dm2。
【点睛】本题考查的关键在于明确切割后的图形表面积增加或减少了哪几个面。并注意单位陷阱,是否需要单位换算。
13.×
【分析】根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】÷=×=
a等于,所以本题说法错误。
故答案为:×
【点睛】明确已知一个数的几分之几是多少,求这个数,用除法解答,是解答此题的关键。
14.√
【分析】根据正方体和长方体的体积公式判断此题,据此判断。
【详解】正方体的体积=长×宽×高=底面积×高
长方体的体积=长×宽×高=底面积×高
原题说法正确。
故答案为:√
【点睛】本题涉及的考点较多,但都属于基础题,要牢记有关知识点的概念,并熟练运用。
15.√
【分析】根据生活经验和实际情况,对体积单位和数据大小的认识,可知计量一个电视机外壳的体积用“立方分米”做单位;由此解答。
【详解】根据分析可知,一个25寸电视机外壳的体积约是1.5立方分米。
原题干说法正确。
故答案为:√
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
16.×
【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此判断即可。
【详解】正方体的棱长扩大2倍,它的表面积就扩大倍。
体积扩大倍。
因此,正方体的棱长扩大2倍,则表面积和体积都扩大4倍。这种说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握正方体的表面积公式、因数与积的变化规律及应用。
17.×
【分析】倒数的意义:乘积是1的两个数叫做互为倒数,倒数是互相依存的,据此分析判断。
【详解】因为,所以是7的倒数,或7是的倒数,不能说和7都是倒数,所以因为,所以和7都是倒数的说法是错误的;
故答案为:×
【点睛】本题主要考查倒数的意义,注意倒数是互相依存的。
18.;;;0
;;22;
【详解】略
19.表面积:344cm2
体积:420cm3
【分析】根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】表面积:(10×7+10×6+7×6)×2
=(70+60+42)×2
=172×2
=344(cm2)
体积:10×7×6=420(cm3)
20.×=
【分析】先这个正方形的面积看作单位“1”,把它平均分成6份,其中5份涂色,是整个正方形的,再把每份平均分成5小份,每小份是的,其中1小份涂色,是整个正方形的的,根据分数乘法的意义,用乘即可。
【详解】
×==
21.
【分析】根据题意可知,把这份计划看作单位“1”,上半月完成了这份计划的,下半月和上半月完成的同样多,则下半月也完成了这份计划的,根据分数减法的意义,用+-1即可求出超额完成了几分之几。
【详解】+-1
=-1
=
答:超额完成了。
【点睛】本题考查了分数加减法的计算和混合应用。
22.106厘米;792平方厘米
【分析】根据题意可知,需要彩带总长等于2条长+2条宽+4条高+打结处彩带长20厘米,即可求出需要彩带的总长度;
求做这样一个礼盒至少需要的纸盒多少平方厘米,就是求这个礼盒的表面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】12×2+15×2+8×4+20
=24+30+32+20
=54+32+20
=86+20
=106(厘米)
(12×15+12×8+15×8)×2
=(180+96+120)×2
=(276+120)×2
=396×2
=792(平方厘米)
答:至少需要准备106厘米的彩带,做这样一个礼盒至少需要792平方厘米。
【点睛】本题主要考查长方体棱长总和与表面积公式的应用。
23.176平方分米;160升
【分析】1米=10分米,无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用4×4+4×10×2+4×10×2即可求出无盖的长方体铁皮箱的表面积。根据长方体的体积=长×宽×高,用4×4×10即可求出这只水桶的体积,再把单位换算成升。
【详解】1米=10分米
4×4+4×10×2+4×10×2
=16+80+80
=176(平方分米)
4×4×10=160(立方分米)
160立方分米=160升
答:做一只这样的水桶至少要176平方分米铁皮;这只水桶能装水160升。
【点睛】本题主要考查了长方体表面积公式和体积公式的灵活应用,关键是明确表面积有几个面。
24.16千克
【分析】根据题意,把这种蜂蜜的质量看作单位“1”,根据分数乘法的意义,用这种蜂蜜质量×,即可求出果糖和葡萄糖共有多少千克。
【详解】20×=16(千克)
答:其中果糖和葡萄糖共有16千克。
【点睛】本题考查分数乘法的应用题,解题关键是找出题目中的单位“1”是哪个量,再根据分数乘法的意义,进行列数解答。
25.(1)700平方厘米
(2)1200立方厘米
【分析】(1)根据长方体的特点,有4个长,4个宽,4个高,一般长方体的长宽高的长度不同,由此即可知道长方体的长是15厘米,宽是8厘米,高是10厘米,根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
(2)根据长方体的体积公式:长×宽×高,把数代入公式即可求解。
【详解】(1)(15×8+15×10+8×10)×2
=(120+150+80)×2
=350×2
=700(平方厘米)
答:长方体盒子的表面积是700平方厘米。
(2)15×8×10
=120×10
=1200(立方厘米)
答:长方体盒子的体积是1200立方厘米。
【点睛】本题主要考查长方体的展开图以及它的表面积和体积公式,熟练掌握它们的公式并灵活运用。
26.250立方厘米
【分析】由题意可知:上升部分的水的体积等于皇冠的体积,先求出水面上升的高度,再用上升的高度×长方体的底面积即可。
【详解】(12.5-12)×(25×20)
=0.5×500
=250(立方厘米)
答:皇冠的体积是250立方厘米。
【点睛】本题主要考查不规则物体体积的计算方法,理解上升部分的水的体积等于皇冠的体积是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
