高中数学人教A版(2019)选必修2 课时作业5 等差数列的综合应用(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)选必修2 课时作业5 等差数列的综合应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 401.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
课时作业5 等差数列的综合应用
题组一 由等差数列构造新的等差数列
1. 在等差数列 中, , ,则 的值为( )
A. 30 B. 27 C. 24 D. 21
2. 已知数列 , 都是等差数列,公差分别为 , ,数列 满足 ,则数列 的公差为 .
3. 已知 是等差数列,且 , .
(1) 求数列 的通项公式;
(2) 若从数列 中,依次取出第2项,第4项,第6项, ,第 项,按原来的顺序组成一个新数列 ,求 的通项公式.
.
题组二 等差数列的实际应用
4. [2022山东威海高二期末]偿还银行贷款时,“等额本金还款法”是一种很常见的还款方式,其本质是将本金平均分配到每一期进行偿还,每一期的还款金额由两部分组成,一部分为每期本金,即贷款本金除以还款期数,另一部分是利息,即贷款本金与已还本金总额的差乘利率.自主创业的大学生张华向银行贷款的本金为48万元,张华跟银行约定,按照等额本金还款法,每个月还一次款,20年还清,贷款月利率为 ,设张华第 个月的还款金额为 元,则 ( )
A. 2 192 B. C. D.
5. 1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到200这200个数中,被4除余2,且被6除余2的数按从小到大的顺序排成一列,构成数列 ,则这个数列中的最大项为( )
A. 200 B. 194 C. 182 D. 198
题组三 等差数列与其他知识的交汇问题
6. 等差数列 中, , 是方程 的两根,则 的值为( )
A. 2 B. 3 C. D.
7. 已知函数 ,数列 满足 , .
(1) 判断数列 是不是等差数列,并说明理由;
(2) 求数列 的通项公式.
8. 在 中, 、 、 所对的边分别为 , , ,已知 , , 成等差数列.
(1) 证明: , , 成等差数列;
(2) 求角 的取值范围.
9. 多选题已知 , 是等差数列,则下列数列是等差数列的是( )
A. B. C. D.
10. [2023湖北武汉高二测试](多选题)在无穷等差数列 中,首项 ,公差 ,依次取出项的序号被4除余3的项组成数列 ,则( )
A.
B.
C.
D. 中的第503项是 中的第2 020项
11. 图1是第七届国际数学教育大会的会徽图案,会徽的主体图案是由图2所示的一连串直角三角形演化而成的,其中 ,若把图2中的直角三角形继续作下去,记 , , , 的长度构成的数列为 ,则此数列的通项公式为 ( )
图1 图2
A. B. C. D.
12. 已知两个等差数列 ,8,11, 与 ,7,11, ,它们的公共项组成数列 ,则数列 的通项公式为 ;若数列 和 的项数均为100,则 的项数是 .
命题分析 本题主要考查了等差数列的性质及通项公式的应用,确定新等差数列的公差是求解问题的关键.
答题要领 由已知结合等差数列的性质确定 的公差及通项公式,进而可求.
解题感悟 若两个等差数列 和 中存在公共项,且公差分别为 和 ,则由它们的公共项组成的数列也为等差数列,且公差为 与 的最小公倍数.
13. [2023湖北宜昌高二测试]设三个数 ,3, 成等差数列,则点 的轨迹方程是 .
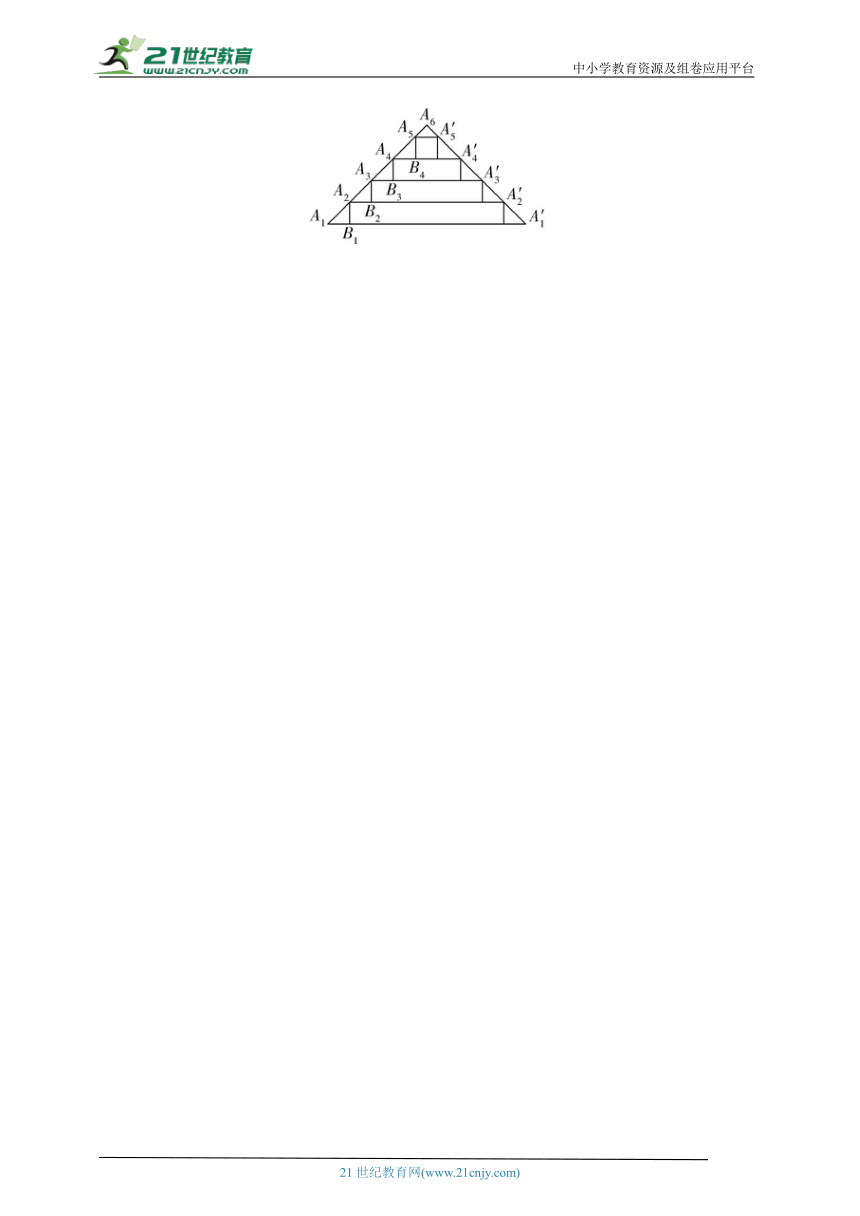
14. 中国古代的武成王庙是专门祭祀姜太公以及历代良臣名将的庙宇,这类庙宇的顶部构造颇有讲究.武成王庙顶部的剖面直观图如图所示,其中 , , ,且数列 是第二项为 的等差数列.若以 为坐标原点, , 的方向分别为 , 轴的正方向建立平面直角坐标系,则直线 的斜率为0.4.
课时作业5 等差数列的综合应用
题组一 由等差数列构造新的等差数列
1. 在等差数列 中, , ,则 的值为( )
A. 30 B. 27 C. 24 D. 21
【答案】A
【解析】设 , , .
因为 是等差数列,所以 , , 也成等差数列,
所以 ,所以 ,即 .
2. 已知数列 , 都是等差数列,公差分别为 , ,数列 满足 ,则数列 的公差为 .
【答案】
【解析】易知数列 为等差数列,且公差为 .
3. 已知 是等差数列,且 , .
(1) 求数列 的通项公式;
【解析】设等差数列 的公差为 , , .
, , , .
(2) 若从数列 中,依次取出第2项,第4项,第6项, ,第 项,按原来的顺序组成一个新数列 ,求 的通项公式.
【解析】 , , , , , .
当 时, , 是以 为首项,4为公差的等差数列 .
题组二 等差数列的实际应用
4. [2022山东威海高二期末]偿还银行贷款时,“等额本金还款法”是一种很常见的还款方式,其本质是将本金平均分配到每一期进行偿还,每一期的还款金额由两部分组成,一部分为每期本金,即贷款本金除以还款期数,另一部分是利息,即贷款本金与已还本金总额的差乘利率.自主创业的大学生张华向银行贷款的本金为48万元,张华跟银行约定,按照等额本金还款法,每个月还一次款,20年还清,贷款月利率为 ,设张华第 个月的还款金额为 元,则 ( )
A. 2 192 B. C. D.
【答案】D
【解析】由题意可知每月偿还的本金为2 000元,则 ,故选 .
5. 1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到200这200个数中,被4除余2,且被6除余2的数按从小到大的顺序排成一列,构成数列 ,则这个数列中的最大项为( )
A. 200 B. 194 C. 182 D. 198
【答案】B
【解析】由题意可知数列 中的项既是4的倍数,又是6的倍数,因此数列 是以2为首项,12为公差的等差数列,即 ,因此 , ,故选 .
题组三 等差数列与其他知识的交汇问题
6. 等差数列 中, , 是方程 的两根,则 的值为( )
A. 2 B. 3 C. D.
【答案】D
【解析】由题意可得 ,又 为等差数列, , .故选 .
7. [2023湖北黄冈高二测试]已知函数 ,数列 满足 , .
(1) 判断数列 是不是等差数列,并说明理由;
【解析】数列 是等差数列,理由如下:
因为 , ,所以 ,
则 ,故 ,
又 ,则 ,所以数列 是以1为首项,1为公差的等差数列.
(2) 求数列 的通项公式.
【解析】由(1)得, ,所以 .
8. [2023陕西渭南高二期中]在 中, 、 、 所对的边分别为 , , ,已知 , , 成等差数列.
(1) 证明: , , 成等差数列;
证明:由 , , 成等差数列,得 ,
由正弦定理 ,得 ,
则 , , 成等差数列.
(2) 求角 的取值范围.
【解析】由(1)得, ,由余弦定理的推论得:
.
因为 , ,所以 ,当且仅当 时等号成立,
则 .
又 ,所以角 的取值范围是 .
9. 多选题已知 , 是等差数列,则下列数列是等差数列的是( )
A. B. C. D.
【答案】ACD
【解析】由 , 是等差数列,可设公差分别为常数 , ,
则
,
, ,
所以 , , 都是等差数列;
对于选项 , ,
不一定是同一个常数,故 不一定是等差数列.
故选 .
10. [2023湖北武汉高二测试](多选题)在无穷等差数列 中,首项 ,公差 ,依次取出项的序号被4除余3的项组成数列 ,则( )
A.
B.
C.
D. 中的第503项是 中的第2 020项
【答案】AC
【解析】 , , ,故 正确;
数列 中项的序号被4除余3的项有第3项,第7项,第11项, ,
, ,故 正确, 错误;
设数列 中的第 项是数列 中的第 项,则 ,
当 时, ,
即数列 中的第503项是 中的第2 011项,故 错误.
故选 .
11. 图1是第七届国际数学教育大会的会徽图案,会徽的主体图案是由图2所示的一连串直角三角形演化而成的,其中 ,若把图2中的直角三角形继续作下去,记 , , , 的长度构成的数列为 ,则此数列的通项公式为 ( )
图1 图2
A. B. C. D.
【答案】B
【解析】因为 , , , , 都是直角三角形,
所以 ,且 ,
所以数列 是以1为首项,1为公差的等差数列,所以 ,又 ,所以 .故选 .
12. 已知两个等差数列 ,8,11, 与 ,7,11, ,它们的公共项组成数列 ,则数列 的通项公式为 ;若数列 和 的项数均为100,则 的项数是 .
命题分析 本题主要考查了等差数列的性质及通项公式的应用,确定新等差数列的公差是求解问题的关键.
答题要领 由已知结合等差数列的性质确定 的公差及通项公式,进而可求.
【答案】 , 25
【解析】由于数列 是以5为首项,3为公差的等差数列,数列 是以3为首项,4为公差的等差数列,所以 也是等差数列,且公差为 ,
又 ,故 .
又 , ,
所以 解得 ,
故 的项数为25.
解题感悟 若两个等差数列 和 中存在公共项,且公差分别为 和 ,则由它们的公共项组成的数列也为等差数列,且公差为 与 的最小公倍数.
13. [2023湖北宜昌高二测试]设三个数 ,3, 成等差数列,则点 的轨迹方程是 .
【答案】
【解析】由 ,3, 成等差数列,
得 ,
点 到 和 的距离之和为6,且 ,
点 的轨迹是以 和 为焦点的椭圆,
设其方程为 ,则 解得
点 的轨迹方程是 .
14. 中国古代的武成王庙是专门祭祀姜太公以及历代良臣名将的庙宇,这类庙宇的顶部构造颇有讲究.武成王庙顶部的剖面直观图如图所示,其中 , , ,且数列 是第二项为 的等差数列.若以 为坐标原点, , 的方向分别为 , 轴的正方向建立平面直角坐标系,则直线 的斜率为0.4.
[解析]由题意可知, ,令 , , ,
则 ,
因为数列 是第二项为 的等差数列,
所以可设公差为 ,则 ,
因为 ,所以 ,同理 ,
则直线 的斜率 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
课时作业5 等差数列的综合应用
题组一 由等差数列构造新的等差数列
1. 在等差数列 中, , ,则 的值为( )
A. 30 B. 27 C. 24 D. 21
2. 已知数列 , 都是等差数列,公差分别为 , ,数列 满足 ,则数列 的公差为 .
3. 已知 是等差数列,且 , .
(1) 求数列 的通项公式;
(2) 若从数列 中,依次取出第2项,第4项,第6项, ,第 项,按原来的顺序组成一个新数列 ,求 的通项公式.
.
题组二 等差数列的实际应用
4. [2022山东威海高二期末]偿还银行贷款时,“等额本金还款法”是一种很常见的还款方式,其本质是将本金平均分配到每一期进行偿还,每一期的还款金额由两部分组成,一部分为每期本金,即贷款本金除以还款期数,另一部分是利息,即贷款本金与已还本金总额的差乘利率.自主创业的大学生张华向银行贷款的本金为48万元,张华跟银行约定,按照等额本金还款法,每个月还一次款,20年还清,贷款月利率为 ,设张华第 个月的还款金额为 元,则 ( )
A. 2 192 B. C. D.
5. 1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到200这200个数中,被4除余2,且被6除余2的数按从小到大的顺序排成一列,构成数列 ,则这个数列中的最大项为( )
A. 200 B. 194 C. 182 D. 198
题组三 等差数列与其他知识的交汇问题
6. 等差数列 中, , 是方程 的两根,则 的值为( )
A. 2 B. 3 C. D.
7. 已知函数 ,数列 满足 , .
(1) 判断数列 是不是等差数列,并说明理由;
(2) 求数列 的通项公式.
8. 在 中, 、 、 所对的边分别为 , , ,已知 , , 成等差数列.
(1) 证明: , , 成等差数列;
(2) 求角 的取值范围.
9. 多选题已知 , 是等差数列,则下列数列是等差数列的是( )
A. B. C. D.
10. [2023湖北武汉高二测试](多选题)在无穷等差数列 中,首项 ,公差 ,依次取出项的序号被4除余3的项组成数列 ,则( )
A.
B.
C.
D. 中的第503项是 中的第2 020项
11. 图1是第七届国际数学教育大会的会徽图案,会徽的主体图案是由图2所示的一连串直角三角形演化而成的,其中 ,若把图2中的直角三角形继续作下去,记 , , , 的长度构成的数列为 ,则此数列的通项公式为 ( )
图1 图2
A. B. C. D.
12. 已知两个等差数列 ,8,11, 与 ,7,11, ,它们的公共项组成数列 ,则数列 的通项公式为 ;若数列 和 的项数均为100,则 的项数是 .
命题分析 本题主要考查了等差数列的性质及通项公式的应用,确定新等差数列的公差是求解问题的关键.
答题要领 由已知结合等差数列的性质确定 的公差及通项公式,进而可求.
解题感悟 若两个等差数列 和 中存在公共项,且公差分别为 和 ,则由它们的公共项组成的数列也为等差数列,且公差为 与 的最小公倍数.
13. [2023湖北宜昌高二测试]设三个数 ,3, 成等差数列,则点 的轨迹方程是 .
14. 中国古代的武成王庙是专门祭祀姜太公以及历代良臣名将的庙宇,这类庙宇的顶部构造颇有讲究.武成王庙顶部的剖面直观图如图所示,其中 , , ,且数列 是第二项为 的等差数列.若以 为坐标原点, , 的方向分别为 , 轴的正方向建立平面直角坐标系,则直线 的斜率为0.4.
课时作业5 等差数列的综合应用
题组一 由等差数列构造新的等差数列
1. 在等差数列 中, , ,则 的值为( )
A. 30 B. 27 C. 24 D. 21
【答案】A
【解析】设 , , .
因为 是等差数列,所以 , , 也成等差数列,
所以 ,所以 ,即 .
2. 已知数列 , 都是等差数列,公差分别为 , ,数列 满足 ,则数列 的公差为 .
【答案】
【解析】易知数列 为等差数列,且公差为 .
3. 已知 是等差数列,且 , .
(1) 求数列 的通项公式;
【解析】设等差数列 的公差为 , , .
, , , .
(2) 若从数列 中,依次取出第2项,第4项,第6项, ,第 项,按原来的顺序组成一个新数列 ,求 的通项公式.
【解析】 , , , , , .
当 时, , 是以 为首项,4为公差的等差数列 .
题组二 等差数列的实际应用
4. [2022山东威海高二期末]偿还银行贷款时,“等额本金还款法”是一种很常见的还款方式,其本质是将本金平均分配到每一期进行偿还,每一期的还款金额由两部分组成,一部分为每期本金,即贷款本金除以还款期数,另一部分是利息,即贷款本金与已还本金总额的差乘利率.自主创业的大学生张华向银行贷款的本金为48万元,张华跟银行约定,按照等额本金还款法,每个月还一次款,20年还清,贷款月利率为 ,设张华第 个月的还款金额为 元,则 ( )
A. 2 192 B. C. D.
【答案】D
【解析】由题意可知每月偿还的本金为2 000元,则 ,故选 .
5. 1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到200这200个数中,被4除余2,且被6除余2的数按从小到大的顺序排成一列,构成数列 ,则这个数列中的最大项为( )
A. 200 B. 194 C. 182 D. 198
【答案】B
【解析】由题意可知数列 中的项既是4的倍数,又是6的倍数,因此数列 是以2为首项,12为公差的等差数列,即 ,因此 , ,故选 .
题组三 等差数列与其他知识的交汇问题
6. 等差数列 中, , 是方程 的两根,则 的值为( )
A. 2 B. 3 C. D.
【答案】D
【解析】由题意可得 ,又 为等差数列, , .故选 .
7. [2023湖北黄冈高二测试]已知函数 ,数列 满足 , .
(1) 判断数列 是不是等差数列,并说明理由;
【解析】数列 是等差数列,理由如下:
因为 , ,所以 ,
则 ,故 ,
又 ,则 ,所以数列 是以1为首项,1为公差的等差数列.
(2) 求数列 的通项公式.
【解析】由(1)得, ,所以 .
8. [2023陕西渭南高二期中]在 中, 、 、 所对的边分别为 , , ,已知 , , 成等差数列.
(1) 证明: , , 成等差数列;
证明:由 , , 成等差数列,得 ,
由正弦定理 ,得 ,
则 , , 成等差数列.
(2) 求角 的取值范围.
【解析】由(1)得, ,由余弦定理的推论得:
.
因为 , ,所以 ,当且仅当 时等号成立,
则 .
又 ,所以角 的取值范围是 .
9. 多选题已知 , 是等差数列,则下列数列是等差数列的是( )
A. B. C. D.
【答案】ACD
【解析】由 , 是等差数列,可设公差分别为常数 , ,
则
,
, ,
所以 , , 都是等差数列;
对于选项 , ,
不一定是同一个常数,故 不一定是等差数列.
故选 .
10. [2023湖北武汉高二测试](多选题)在无穷等差数列 中,首项 ,公差 ,依次取出项的序号被4除余3的项组成数列 ,则( )
A.
B.
C.
D. 中的第503项是 中的第2 020项
【答案】AC
【解析】 , , ,故 正确;
数列 中项的序号被4除余3的项有第3项,第7项,第11项, ,
, ,故 正确, 错误;
设数列 中的第 项是数列 中的第 项,则 ,
当 时, ,
即数列 中的第503项是 中的第2 011项,故 错误.
故选 .
11. 图1是第七届国际数学教育大会的会徽图案,会徽的主体图案是由图2所示的一连串直角三角形演化而成的,其中 ,若把图2中的直角三角形继续作下去,记 , , , 的长度构成的数列为 ,则此数列的通项公式为 ( )
图1 图2
A. B. C. D.
【答案】B
【解析】因为 , , , , 都是直角三角形,
所以 ,且 ,
所以数列 是以1为首项,1为公差的等差数列,所以 ,又 ,所以 .故选 .
12. 已知两个等差数列 ,8,11, 与 ,7,11, ,它们的公共项组成数列 ,则数列 的通项公式为 ;若数列 和 的项数均为100,则 的项数是 .
命题分析 本题主要考查了等差数列的性质及通项公式的应用,确定新等差数列的公差是求解问题的关键.
答题要领 由已知结合等差数列的性质确定 的公差及通项公式,进而可求.
【答案】 , 25
【解析】由于数列 是以5为首项,3为公差的等差数列,数列 是以3为首项,4为公差的等差数列,所以 也是等差数列,且公差为 ,
又 ,故 .
又 , ,
所以 解得 ,
故 的项数为25.
解题感悟 若两个等差数列 和 中存在公共项,且公差分别为 和 ,则由它们的公共项组成的数列也为等差数列,且公差为 与 的最小公倍数.
13. [2023湖北宜昌高二测试]设三个数 ,3, 成等差数列,则点 的轨迹方程是 .
【答案】
【解析】由 ,3, 成等差数列,
得 ,
点 到 和 的距离之和为6,且 ,
点 的轨迹是以 和 为焦点的椭圆,
设其方程为 ,则 解得
点 的轨迹方程是 .
14. 中国古代的武成王庙是专门祭祀姜太公以及历代良臣名将的庙宇,这类庙宇的顶部构造颇有讲究.武成王庙顶部的剖面直观图如图所示,其中 , , ,且数列 是第二项为 的等差数列.若以 为坐标原点, , 的方向分别为 , 轴的正方向建立平面直角坐标系,则直线 的斜率为0.4.
[解析]由题意可知, ,令 , , ,
则 ,
因为数列 是第二项为 的等差数列,
所以可设公差为 ,则 ,
因为 ,所以 ,同理 ,
则直线 的斜率 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
