第七章 平面直角坐标系 单元综合测试卷(含答案) 2023-2024学年人教版数学七年级下册
文档属性
| 名称 | 第七章 平面直角坐标系 单元综合测试卷(含答案) 2023-2024学年人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 521.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览


文档简介
第七章 平面直角坐标系 单元综合测试卷
一、选择题(每小题3分,共30分)
1.若用有序数对(3,6)表示教室中前起第3排、左起第6列的位置,那么前起第2排、左起第4列的位置用有序数对可表示为 ( )
A.(2,4) B.(4,2)
C.(2,4)或(4,2) D.(3,6)
2.点(-3,-1)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.下列数据不能确定物体位置的是 ( )
A.5楼6号
B.北偏东30°
C.大学路19号
D.东经118°,北纬36°
4.如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方形,并且猴山的坐标是(-2,2),则图中熊猫馆的位置用坐标表示为 ( )
A.(1,1) B.(2,2)
C.(1,3) D.(4,4)
5.在平面直角坐标系中,将三角形各点的横坐标都减去3个单位长度,纵坐标保持不变,所得图形与原图形相比 ( )
A.向右平移了3个单位长度
B.向左平移了3个单位长度
C.向上平移了3个单位长度
D.向下平移了3个单位长度
6.将点P(-2,-3)向左平移1个单位长度,再向上平移3个单位长度,则所得到的点的坐标为 ( )
A.(-3,0) B.(-1,6)
C.(-3,-6) D.(-1,0)
7.如果点M(m,-n)在第二象限,则点N(2-m,n-2)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.已知点A的坐标为(-3,-2),点B在y轴上,当A,B两点间的距离最短时,点B的坐标为 ( )
A.(0,-2) B.(-2,0)
C.(-3,0) D.(0,-3)
9.若点B(m+1,3m-5)到两坐标轴的距离相等,则点B的坐标是 ( )
A.(4,4)或(2,2) B.(2,-2)
C.(4,4)或(2,-2) D.(4,4)
10.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边做环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2024次相遇地点的坐标是 ( )
A.(2,0) B.(-1,1)
C.(-2,1) D.(-1,-1)
二、填空题(每小题3分,共15分)
11.若点M(a+1,4)在坐标轴上,则点M的坐标为 .
12.如图,已知校门的位置是(1,1),其中一个单位长度表示100米,那么下列对于实验楼的位置的叙述正确的是 .(填序号)
①实验楼的位置是(3,2);②实验楼的位置是(3,3);③实验楼的位置是校门的东北方向200米处.
13.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是 .
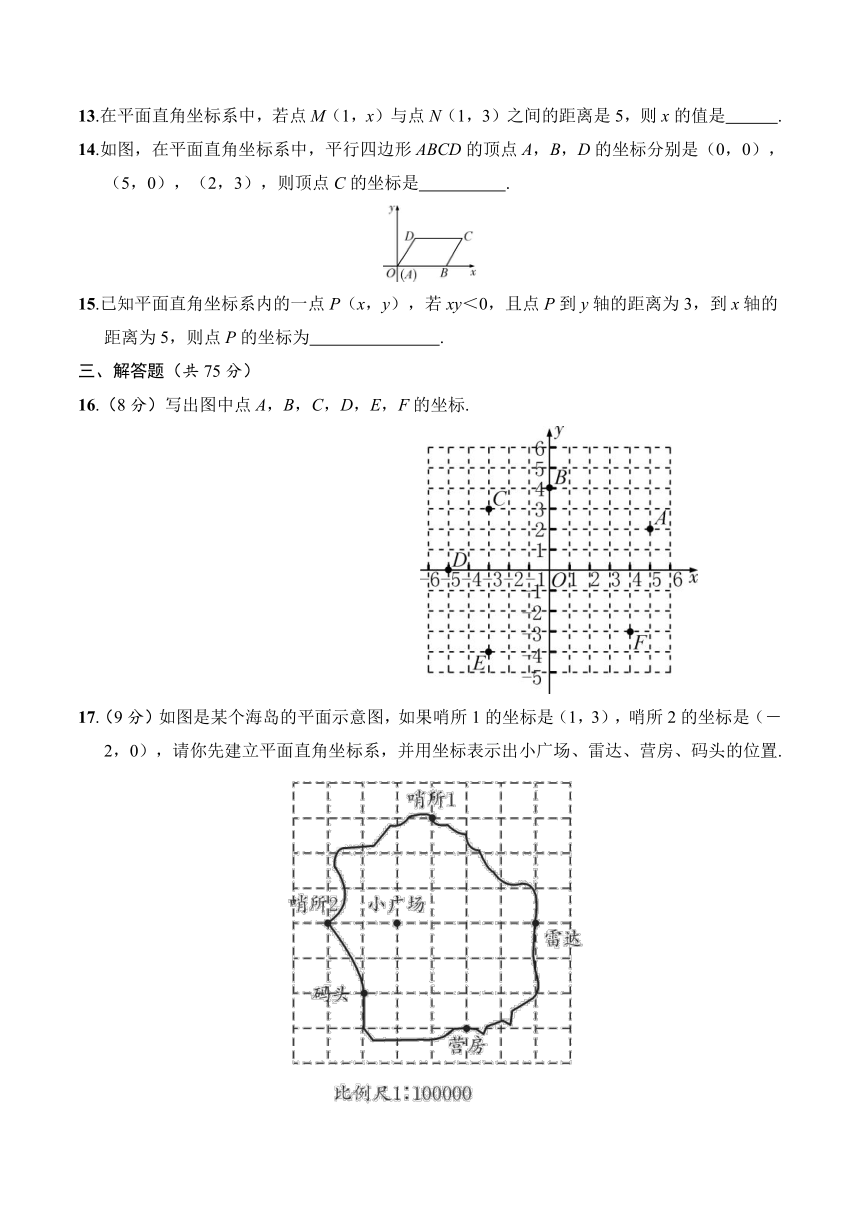
14.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是 .
15.已知平面直角坐标系内的一点P(x,y),若xy<0,且点P到y轴的距离为3,到x轴的距离为5,则点P的坐标为 .
三、解答题(共75分)
16.(8分)写出图中点A,B,C,D,E,F的坐标.
17.(9分)如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
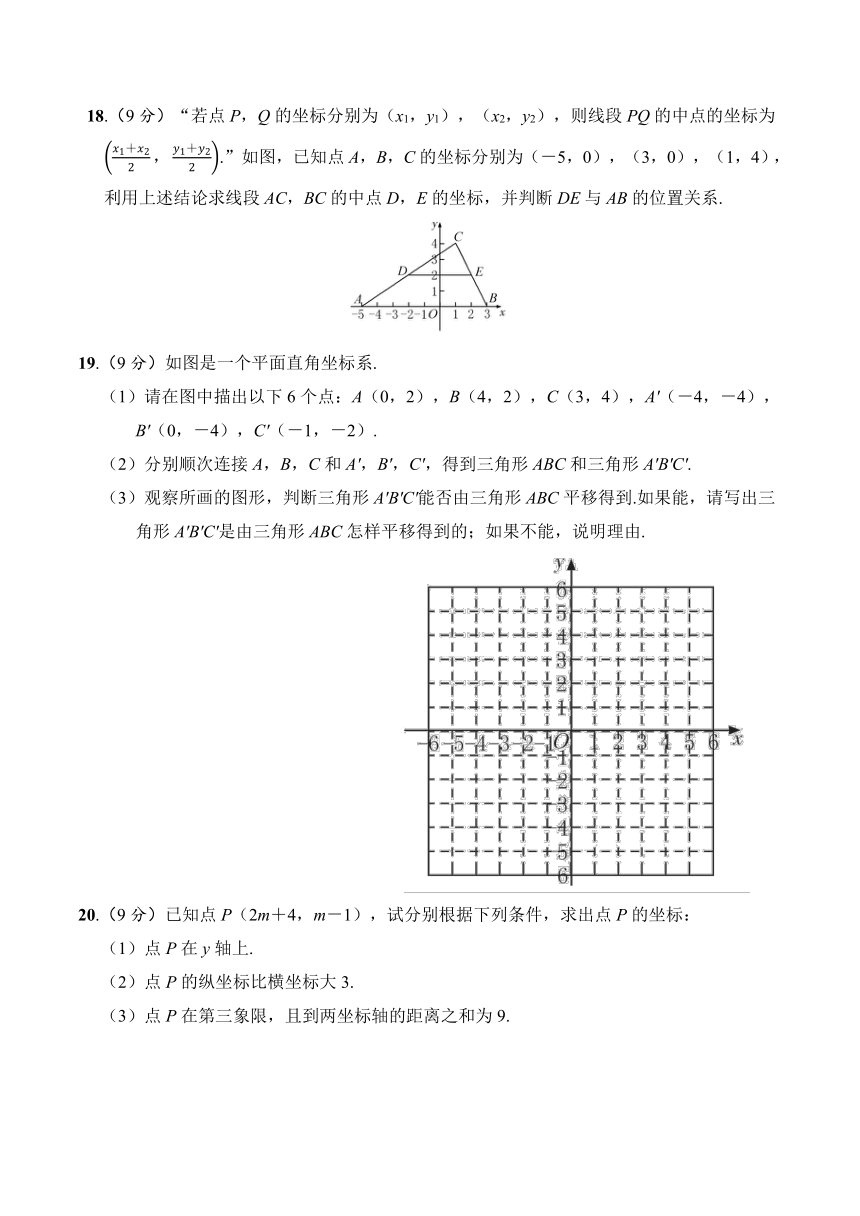
18.(9分)“若点P,Q的坐标分别为(x1,y1),(x2,y2),则线段PQ的中点的坐标为.”如图,已知点A,B,C的坐标分别为(-5,0),(3,0),(1,4),利用上述结论求线段AC,BC的中点D,E的坐标,并判断DE与AB的位置关系.
19.(9分)如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2),B(4,2),C(3,4),A'(-4,-4),B'(0,-4),C'(-1,-2).
(2)分别顺次连接A,B,C和A',B',C',得到三角形ABC和三角形A'B'C'.
(3)观察所画的图形,判断三角形A'B'C'能否由三角形ABC平移得到.如果能,请写出三角形A'B'C'是由三角形ABC怎样平移得到的;如果不能,说明理由.
20.(9分)已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上.
(2)点P的纵坐标比横坐标大3.
(3)点P在第三象限,且到两坐标轴的距离之和为9.
21.(10分)如图,在平面直角坐标系内,已知点A的坐标为(-5,0).
(1)图中点B的坐标是 ,点C的坐标是 ,点D的坐标是 .
(2)求三角形ABC的面积.
(3)在y轴上找一点F,当S三角形ADF=S三角形ABC时,点F的坐标是什么?(直接写出点F的坐标,并在图中画出)
22.(10分)在平面直角坐标系中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(-3,3),C(4,3);
第二组:D(-2,-1),E(2,-1).
(1)直接写出线段AC与线段DE的位置关系: .
(2)在(1)条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM,DM,CM,EM,补全图形,用等式表示∠CAM,∠AMD,∠MDE之间的数量关系,并证明;
②当点M在线段OB的延长线上时,连接AM,DM,请直接写出∠CAM,∠AMD,∠MDE之间的数量关系.
请仔细观察你画出的图形,你还能得出什么结论?
23.(11分)在平面直角坐标系xOy中有不重合的两点A(x1,y1)和B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为;若y1=y2,则AB∥x轴,且线段AB的长度为.
(1)若点A(-1,1),B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,CD=2,则点D的坐标为 .
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=+.例如:图①中,点M(-1,1)与点N(1,-2)之间的折线距离为d(M,N)=+=2+3=5.
解决下列问题:
(1)如图②,已知点E(2,0),H(1,t),若d(E,H)=3,则t= .
(2)如图③,已知点P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).
参考答案
一、选择题(每小题3分,共30分)
ACBCB ADACD
二、填空题(每小题3分,共15分)
11.(0,4) .
12. ② .
13. -2或8 .
14. (7,3) .
15. (3,-5)或(-3,5) .
三、解答题(共75分)
16.解:点A,B,C,D,E,F的坐标分别为A(5,2),B(0,4),C(-3,3),D(-5,0),E(-3,-4),F(4,-3).
17.
解:建立平面直角坐标系如图所示.小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2).
18.解:由“中点公式”及点A,B,C的坐标(-5,0),(3,0),(1,4),得D(-2,2),E(2,2).∵点D,E的纵坐标相等,∴DE∥x轴.又AB在x轴上,∴DE∥AB.
19.
解:(1)如图所示.
(2)如图所示,三角形ABC和三角形A'B'C'即为所求.
(3)能.三角形A'B'C'是由三角形ABC先向左平移4个单位长度,再向下平移6个单位长度得到的.(答案不唯一)
20.
解:(1)∵点P在y轴上,∴2m+4=0.解得m=-2,则m-1=-3.故P(0,-3).
(2)∵点P的纵坐标比横坐标大3,∴m-1-(2m+4)=3.解得m=-8,则2m+4=-12,m-1=-9.故P(-12,-9).
(3)∵点P在第三象限,且到两坐标轴的距离之和为9,∴-(2m+4)+=9.解得m=-4,则2m+4=-4,m-1=-5.故P(-4,-5).
21.(1) (-3,4) , (3,-4) , (5,0) .
解:(2)由图可知,S三角形ABC=S三角形OAB+S三角形AOC=×5×4+×5×4=20.
(3)点F的坐标是(0,4)或(0,-4),点F所有可能的位置如图所示.
22.(1) AC∥DE .
解:(2)①∠CAM+∠MDE=∠AMD.证明如下:如图,过点M作直线MN∥AC.又AC∥DE,∴MN∥AC∥DE.∴∠CAM=∠AMN,∠DMN=∠MDE.∴∠CAM+∠MDE=∠AMN+∠DMN=∠AMD.
②∠MDE=∠AMD+∠CAM.
(3)结论:当点M在线段OB上运动时,∠ACM+∠MED=∠CME.(答案不唯一)
23.(1) 3 .
(2) (1,2)或(1,-2) .
解决下列问题:
(1)t= 2或-2 .
(2)
解:∵点Q在x轴上,∴设点Q的坐标为(x,0).∵三角形OPQ的面积为3,∴××3=3.解得x=±2.当点Q的坐标为(2,0)时,d(P,Q)=+=4;当点Q的坐标为(-2,0)时,d(P,Q)=+=8.综上所述,d(P,Q)为4或8.
一、选择题(每小题3分,共30分)
1.若用有序数对(3,6)表示教室中前起第3排、左起第6列的位置,那么前起第2排、左起第4列的位置用有序数对可表示为 ( )
A.(2,4) B.(4,2)
C.(2,4)或(4,2) D.(3,6)
2.点(-3,-1)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.下列数据不能确定物体位置的是 ( )
A.5楼6号
B.北偏东30°
C.大学路19号
D.东经118°,北纬36°
4.如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方形,并且猴山的坐标是(-2,2),则图中熊猫馆的位置用坐标表示为 ( )
A.(1,1) B.(2,2)
C.(1,3) D.(4,4)
5.在平面直角坐标系中,将三角形各点的横坐标都减去3个单位长度,纵坐标保持不变,所得图形与原图形相比 ( )
A.向右平移了3个单位长度
B.向左平移了3个单位长度
C.向上平移了3个单位长度
D.向下平移了3个单位长度
6.将点P(-2,-3)向左平移1个单位长度,再向上平移3个单位长度,则所得到的点的坐标为 ( )
A.(-3,0) B.(-1,6)
C.(-3,-6) D.(-1,0)
7.如果点M(m,-n)在第二象限,则点N(2-m,n-2)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
8.已知点A的坐标为(-3,-2),点B在y轴上,当A,B两点间的距离最短时,点B的坐标为 ( )
A.(0,-2) B.(-2,0)
C.(-3,0) D.(0,-3)
9.若点B(m+1,3m-5)到两坐标轴的距离相等,则点B的坐标是 ( )
A.(4,4)或(2,2) B.(2,-2)
C.(4,4)或(2,-2) D.(4,4)
10.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边做环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2024次相遇地点的坐标是 ( )
A.(2,0) B.(-1,1)
C.(-2,1) D.(-1,-1)
二、填空题(每小题3分,共15分)
11.若点M(a+1,4)在坐标轴上,则点M的坐标为 .
12.如图,已知校门的位置是(1,1),其中一个单位长度表示100米,那么下列对于实验楼的位置的叙述正确的是 .(填序号)
①实验楼的位置是(3,2);②实验楼的位置是(3,3);③实验楼的位置是校门的东北方向200米处.
13.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是 .
14.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是 .
15.已知平面直角坐标系内的一点P(x,y),若xy<0,且点P到y轴的距离为3,到x轴的距离为5,则点P的坐标为 .
三、解答题(共75分)
16.(8分)写出图中点A,B,C,D,E,F的坐标.
17.(9分)如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
18.(9分)“若点P,Q的坐标分别为(x1,y1),(x2,y2),则线段PQ的中点的坐标为.”如图,已知点A,B,C的坐标分别为(-5,0),(3,0),(1,4),利用上述结论求线段AC,BC的中点D,E的坐标,并判断DE与AB的位置关系.
19.(9分)如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2),B(4,2),C(3,4),A'(-4,-4),B'(0,-4),C'(-1,-2).
(2)分别顺次连接A,B,C和A',B',C',得到三角形ABC和三角形A'B'C'.
(3)观察所画的图形,判断三角形A'B'C'能否由三角形ABC平移得到.如果能,请写出三角形A'B'C'是由三角形ABC怎样平移得到的;如果不能,说明理由.
20.(9分)已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上.
(2)点P的纵坐标比横坐标大3.
(3)点P在第三象限,且到两坐标轴的距离之和为9.
21.(10分)如图,在平面直角坐标系内,已知点A的坐标为(-5,0).
(1)图中点B的坐标是 ,点C的坐标是 ,点D的坐标是 .
(2)求三角形ABC的面积.
(3)在y轴上找一点F,当S三角形ADF=S三角形ABC时,点F的坐标是什么?(直接写出点F的坐标,并在图中画出)
22.(10分)在平面直角坐标系中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(-3,3),C(4,3);
第二组:D(-2,-1),E(2,-1).
(1)直接写出线段AC与线段DE的位置关系: .
(2)在(1)条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM,DM,CM,EM,补全图形,用等式表示∠CAM,∠AMD,∠MDE之间的数量关系,并证明;
②当点M在线段OB的延长线上时,连接AM,DM,请直接写出∠CAM,∠AMD,∠MDE之间的数量关系.
请仔细观察你画出的图形,你还能得出什么结论?
23.(11分)在平面直角坐标系xOy中有不重合的两点A(x1,y1)和B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为;若y1=y2,则AB∥x轴,且线段AB的长度为.
(1)若点A(-1,1),B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,CD=2,则点D的坐标为 .
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=+.例如:图①中,点M(-1,1)与点N(1,-2)之间的折线距离为d(M,N)=+=2+3=5.
解决下列问题:
(1)如图②,已知点E(2,0),H(1,t),若d(E,H)=3,则t= .
(2)如图③,已知点P(3,3),点Q在x轴上,且三角形OPQ的面积为3,求d(P,Q).
参考答案
一、选择题(每小题3分,共30分)
ACBCB ADACD
二、填空题(每小题3分,共15分)
11.(0,4) .
12. ② .
13. -2或8 .
14. (7,3) .
15. (3,-5)或(-3,5) .
三、解答题(共75分)
16.解:点A,B,C,D,E,F的坐标分别为A(5,2),B(0,4),C(-3,3),D(-5,0),E(-3,-4),F(4,-3).
17.
解:建立平面直角坐标系如图所示.小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2).
18.解:由“中点公式”及点A,B,C的坐标(-5,0),(3,0),(1,4),得D(-2,2),E(2,2).∵点D,E的纵坐标相等,∴DE∥x轴.又AB在x轴上,∴DE∥AB.
19.
解:(1)如图所示.
(2)如图所示,三角形ABC和三角形A'B'C'即为所求.
(3)能.三角形A'B'C'是由三角形ABC先向左平移4个单位长度,再向下平移6个单位长度得到的.(答案不唯一)
20.
解:(1)∵点P在y轴上,∴2m+4=0.解得m=-2,则m-1=-3.故P(0,-3).
(2)∵点P的纵坐标比横坐标大3,∴m-1-(2m+4)=3.解得m=-8,则2m+4=-12,m-1=-9.故P(-12,-9).
(3)∵点P在第三象限,且到两坐标轴的距离之和为9,∴-(2m+4)+=9.解得m=-4,则2m+4=-4,m-1=-5.故P(-4,-5).
21.(1) (-3,4) , (3,-4) , (5,0) .
解:(2)由图可知,S三角形ABC=S三角形OAB+S三角形AOC=×5×4+×5×4=20.
(3)点F的坐标是(0,4)或(0,-4),点F所有可能的位置如图所示.
22.(1) AC∥DE .
解:(2)①∠CAM+∠MDE=∠AMD.证明如下:如图,过点M作直线MN∥AC.又AC∥DE,∴MN∥AC∥DE.∴∠CAM=∠AMN,∠DMN=∠MDE.∴∠CAM+∠MDE=∠AMN+∠DMN=∠AMD.
②∠MDE=∠AMD+∠CAM.
(3)结论:当点M在线段OB上运动时,∠ACM+∠MED=∠CME.(答案不唯一)
23.(1) 3 .
(2) (1,2)或(1,-2) .
解决下列问题:
(1)t= 2或-2 .
(2)
解:∵点Q在x轴上,∴设点Q的坐标为(x,0).∵三角形OPQ的面积为3,∴××3=3.解得x=±2.当点Q的坐标为(2,0)时,d(P,Q)=+=4;当点Q的坐标为(-2,0)时,d(P,Q)=+=8.综上所述,d(P,Q)为4或8.
