2024年高考物理二轮复习专题 课件★★ 带电粒子在复合场中的运动 课件(共68张PPT)
文档属性
| 名称 | 2024年高考物理二轮复习专题 课件★★ 带电粒子在复合场中的运动 课件(共68张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-15 00:00:00 | ||
图片预览







文档简介
(共68张PPT)
2024年高考物理二轮复习专题 课件★★ 带电粒子在复合场中的运动
考点一
带电粒子在组合场中的运动
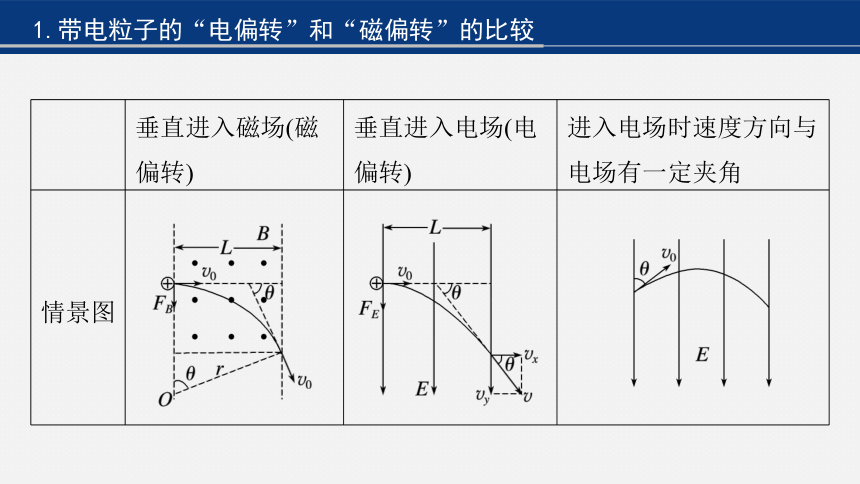
1.带电粒子的“电偏转”和“磁偏转”的比较
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
情景图
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
受力 FB=qv0B,FB大小不变,方向变化,方向总指向圆心,FB为变力 FE=qE,FE大小、方向均不变,FE为恒力 FE=qE,FE大小、方向均不变,FE为恒力
运动规律
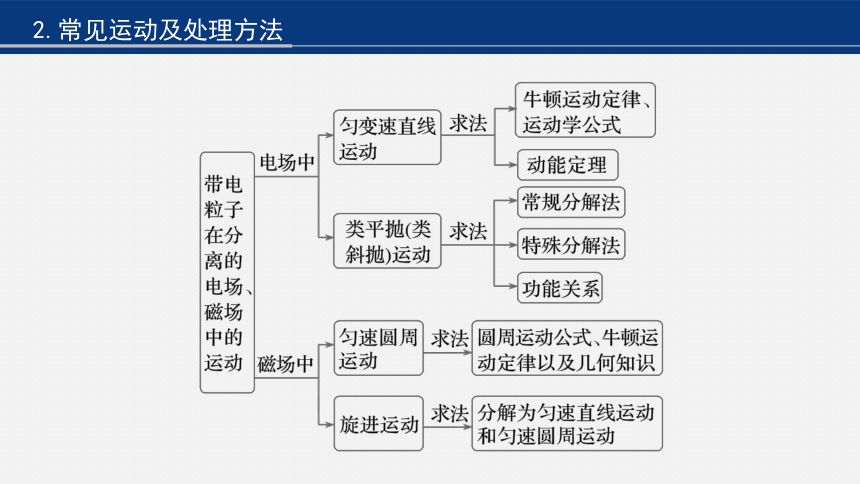
2.常见运动及处理方法
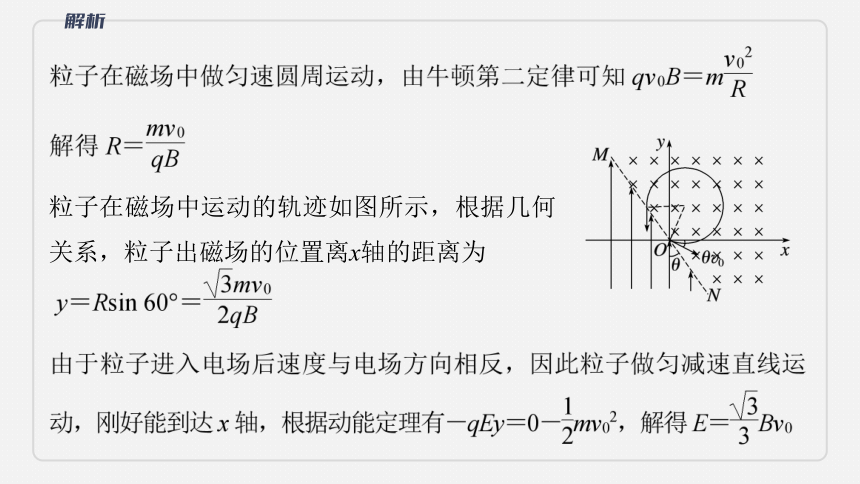
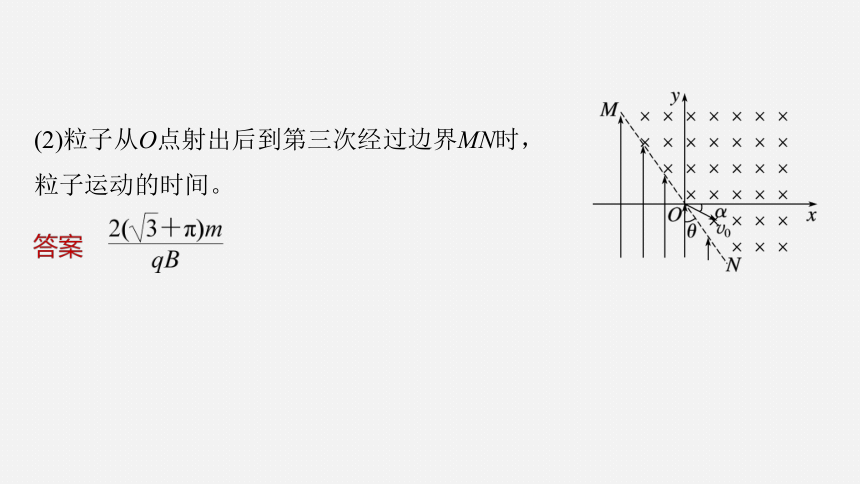
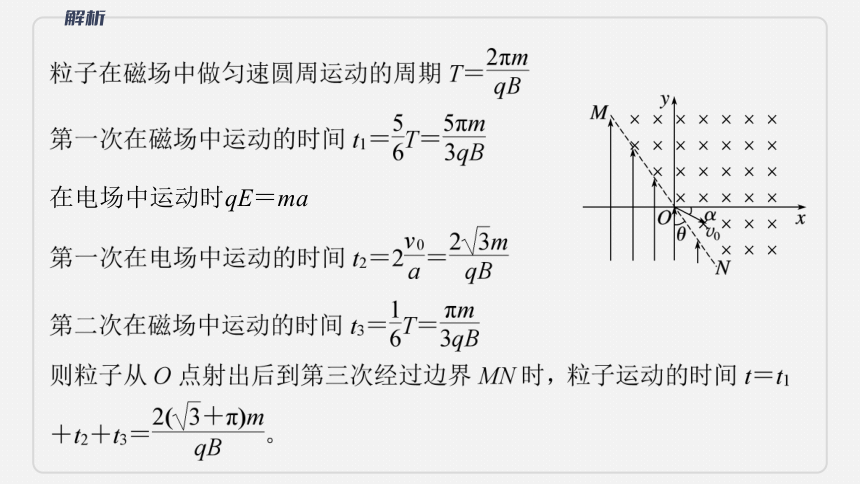
(2023·江苏省模拟)如图所示,在xOy坐标系中,有垂直坐标平面向里的匀强磁场和沿y轴正向的匀强电场,匀强磁场的磁感应强度为B,电场和磁场的分界线为MN,MN穿过坐标原点和二、四象限,与y轴的夹角为θ=30°。一个质量为m、电荷量为q的带正电粒子,在坐标原点以大小为v0、方向与x轴正向成α=30°角的初速度射入磁场,粒子经磁场偏转进入电场后,恰好能到达x轴。
不计粒子的重力,求:
例1
粒子在磁场中运动的轨迹如图所示,根据几何关系,粒子出磁场的位置离x轴的距离为
(2)粒子从O点射出后到第三次经过边界MN时,粒子运动的时间。
在电场中运动时qE=ma
(2023·江苏扬州市一模)如图所示,第一象限内存在垂直于纸面向里的匀强磁场;第四象限内存在沿+y轴的匀强电场,电场强度大小为E= 。t=0时刻,粒子从P点以速度v0平行+x轴射入电场,第1次通过x轴从Q点进入磁场。已知P点坐标为(0,-l),粒子质量为m、电荷量为+q,重力不计。
(1)求粒子经过Q点的速度v;
例2
粒子从P到Q做类平抛运动,轨迹如图甲所示,
解得α=45°
(2)欲使粒子不从y轴射出磁场,求磁感应强度的最小值Bm;
Q点到O点的距离s=2l,粒子进入磁场做匀速圆周运动,轨道半径为R,
欲使粒子不从y轴射出磁场,临界状态轨迹如图甲中圆弧部分
根据几何关系R+Rsin α=2l,
(3)若磁感应强度B= ,求粒子第5次通过x轴的位置x和时间t。
返回电场后做类斜抛运动,运动轨迹如图乙所示
总结提升
“5步”突破带电粒子在组合场中的运动问题
考点二
带电粒子在叠加场中的运动
1.三种典型情况
(1)若只有两个场,所受合力为零,则表现为匀速直线运动状态或静止状态。例如电场与磁场叠加满足qE=qvB时,重力场与磁场叠加满足mg=qvB时,重力场与电场叠加满足mg=qE时。
(2)若三场共存,所受合力为零时,粒子做匀速直线运动,其中洛伦兹力F=qvB的方向与速度v垂直。
2.分析
(2023·江苏卷·16)霍尔推进器某局部区域可抽象成如图所示的模型。Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B。质量为m、电荷量为e的电子从O点沿x轴正方向水平入射。入射速度为v0时,电子沿x轴做直线运动;入射速度小于v0时,电子的运动轨迹如图中的虚线所示,且在最高点与在最低点所受的合力大小相等。不计重力及电子间相互作用。
(1)求电场强度的大小E;
例3
答案 v0B
由题知,入射速度为v0时,电子沿x轴做直线运动,则有Ee=ev0B
解得E=v0B
(3)若电子入射速度在0答案 90%
方法一 若电子以速度v入射时,设电子能到达的最高点位置的纵坐标为y,则根据动能定理有
由于电子在最高点与在最低点所受的合力大小相等,则在最高点有F合=evmB-eE
在最低点有F合=eE-evB
方法二 如果电子在复合场中受到的电场力与洛伦兹力等值反向,电子做匀速直线运动。如果这两个力不平衡,可将其分解为匀速直线运动和匀速圆周运动两个分运动。对于初状态静止的电子,设Ee=ev1B,可看作以v1=v0对应水平向右的匀速直线运动,而另一个分运动是v2=-v0,
设速度为v的电子,一个分运动为v1=v0,对应水平向右的匀速直线运动。另一个分运动的速度为v2,这个分运动做圆周运动的直径为y2,
电子入射速度为两个分速度的合速度,
在0由于电子在0总结提升
配速法其实就是给物体配一个速度v,使得这个速度所产生的洛伦兹力与题目中的重力或者电场力(视情况而定)抵消,对应的,还会出现一个与v等大反向的速度v′,此时等效为只受到一个洛伦兹力,而不再是重力或者电场力加上洛伦兹力,从而降低分析难度。
配速法
(1)求进入第1组磁场区的粒子的速度大小v;
答案 2v0
解得v=2v0
(2)调节磁场宽度,恰好使所有带电粒子都不能从第1组磁场的右边界穿出,求磁场的宽度Δx;
答案 d
粒子进入磁场时,速度方向与y轴负方向的夹角θ越小,粒子越容易射出磁场,θ的最小值为θ=60°
由几何关系可得Δx=R+Rcos θ
解得磁场的宽度Δx=d
设粒子在第n层磁场中运动的速度为vn,轨迹半径为rn(下标表示粒子所在组数),
1
2
3
4
1.如图所示,坐标系xOy的第一象限存在匀强磁场,磁场方向垂直于xOy平面向外;第四象限内有沿x轴负方向的匀强电场。质量为m、带电荷量为q(q>0)的粒子以速率v从y轴的点A(0, L)射入磁场,经x轴上的点C(L,0)沿y轴负方向进入电场,然后从y轴负半轴D点以与y轴负方向成60°角离开电场,不计粒子重力,求:
(1)粒子在A点时速度方向与y轴正方向的夹角θ;
答案 120°
1
2
3
4
根据题意,画出粒子的运动轨迹,如图所示
解得R=2L
由几何关系有θ=180°-(90°-∠OAO′)
解得θ=120°
1
2
3
4
(2)匀强电场的电场强度大小;
1
2
3
4
垂直电场方向上有y=vt2
1
2
3
4
(3)粒子在磁场和电场中运动的总时间t。
1
2
3
4
粒子在磁场和电场中运动的总时间
1
2
3
4
1
2
3
4
(1)求第一象限内所加电场的电场强度;
1
2
3
4
在第一象限内,电子做类平抛运动
根据牛顿第二定律得eE=ma
1
2
3
4
(2)若磁场充满第二象限,电子将从x轴上某点离开第二象限,求该点的坐标;
答案 (-2L,0)
1
2
3
4
根据几何关系可知x1=R+Rcos θ=2L
该点的坐标为(-2L,0)
1
2
3
4
(3)若磁场是一个圆形有界磁场,要使电子经磁场偏转后通过x轴时,与y轴负方向的夹角为30°,求圆形磁场区域的最小面积。
1
2
3
4
根据题意,作出轨迹图如图所示
1
2
3
4
3.如图所示,在竖直平面内x轴的上方空间内存在水平向右的匀强电场,x轴的下方空间内存在垂直纸面向外的匀强磁场和竖直向下的匀强电场,磁感应强度大小为0.3 T,电场强度大小均为1.2 V/m。一个带电小球用一根细线悬挂在x轴的上方区域,静止时细线与竖直方向夹角为θ=45°。现将细线剪断,小球运动1 s时第一次经过x轴进
入x轴下方区域。g取10 m/s2。求:(tan 63°≈2)
(1)小球第一次经过x轴时的速度大小;
1
2
3
4
静电力FE=qE=mgtan θ=mg,
1
2
3
4
将细线剪断后,小球在x轴上方做匀加速直线运动,小球的加速度大小为
1
2
3
4
(2)小球第三次经过x轴时的方向;
1
2
3
4
小球穿过x轴进入x轴下方后,由于小球所受重力mg和小球所受静电力FE等大反向,所以小球所受洛伦兹力为其合外力,小球将在此合外力下做匀速圆周运动。设小球第一次通过A点进入x轴下方,经过时间t2,在B点通过x轴,其第一次圆周运动轨迹示意图如图乙所示,
小球运动的圆弧轨迹对应的圆心角
洛伦兹力为其做圆周运动的向心力,有
1
2
3
4
小球在B点通过x轴,进入x轴上方,其速度方向与x轴上方复合场方向垂直,所以小球将做类平抛运动。设此过程小球运动时间为t3。小球将再次经过x轴,设此时其速度为v2,此过程运动轨迹示意图如丙所示,
1
2
3
4
1
2
3
4
(3)从剪断细线开始到小球第四次经过x轴的时间。
1
2
3
4
小球第三次经过x轴后,在x轴下方再次做匀速圆周运动,设此过程运动时间为t4,
1
2
3
4
4.(2022·江苏卷·15)某装置用电场控制带电粒子运动,工作原理如图所示,矩形ABCD区域内存在多层紧邻的匀强电场,每层的高度均为d,电场强度大小均为E,方向沿竖直方向交替变化,AB边长为12d,BC边长为8d,质量为m、电荷量为+q的粒子流从装置左端中点射入电场,粒子初动能为Ek,入射角为θ,在纸面内运动,不
计重力及粒子间的相互作用力。
(1)当θ=θ0时,若粒子能从CD边射出,
求该粒子通过电场的时间t;
答案 见解析
1
2
3
4
电场方向在竖直方向上,粒子所受静电力在竖直方向上,粒子在水平方向上做匀速直线运动,速度分解如图所示
粒子在水平方向的速度为vx=vcos θ0
1
2
3
4
(2)当Ek=4qEd时,若粒子从CD边射出电场时与轴线OO′的距离小于d,求入射角θ的范围;
答案 见解析
粒子进入电场后只有静电力做功,粒子在竖直方向上反复运动后,根据题意可知最终运动的空间如图所示,
若粒子从OO′上部分离开CD边,则静电力做负功,根据动能定理可知-qEx=Ek1-Ek
1
2
3
4
解得粒子在竖直方向上的最大位移为
xm=4dsin2 θ1
解得θ1<30°
1
2
3
4
1
2
3
4
答案 见解析
设粒子入射角为θ′时,粒子恰好从D点射出,由于粒子进入电场时,在水平方向做匀速直线运动,在竖直方向反复做加速度相同的减速运动,加速运动。粒子的速度
1
2
3
4
粒子在沿电场方向,反复做加速度相同的减速运动,加速运动,则
-2ad=v1d2-(v′sin θ′)2
2ad=v2d2-(v1d)2
-2ad=v3d2-(v2d)2
2ad=v4d2-(v3d)2
-2ad=v5d2-(v4d)2
2ad=v6d2-(v5d)2
则v2d=v4d=v6d=v′sin θ′
v1d=v3d=v5d
则粒子在分层电场中运动时间相等,设为t0,
1
2
3
4
1
2
3
4
代入数据化简可得6cos2θ′-8sin θ′cos θ′+1=0
即tan2θ′-8tan θ′+7=0
解得tan θ′=7(舍去)或tan θ′=1
1
2
3
4
则从CD边出射的粒子入射粒子的数量之比
2024年高考物理二轮复习专题 课件★★ 带电粒子在复合场中的运动
考点一
带电粒子在组合场中的运动
1.带电粒子的“电偏转”和“磁偏转”的比较
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
情景图
垂直进入磁场(磁偏转) 垂直进入电场(电偏转) 进入电场时速度方向与电场有一定夹角
受力 FB=qv0B,FB大小不变,方向变化,方向总指向圆心,FB为变力 FE=qE,FE大小、方向均不变,FE为恒力 FE=qE,FE大小、方向均不变,FE为恒力
运动规律
2.常见运动及处理方法
(2023·江苏省模拟)如图所示,在xOy坐标系中,有垂直坐标平面向里的匀强磁场和沿y轴正向的匀强电场,匀强磁场的磁感应强度为B,电场和磁场的分界线为MN,MN穿过坐标原点和二、四象限,与y轴的夹角为θ=30°。一个质量为m、电荷量为q的带正电粒子,在坐标原点以大小为v0、方向与x轴正向成α=30°角的初速度射入磁场,粒子经磁场偏转进入电场后,恰好能到达x轴。
不计粒子的重力,求:
例1
粒子在磁场中运动的轨迹如图所示,根据几何关系,粒子出磁场的位置离x轴的距离为
(2)粒子从O点射出后到第三次经过边界MN时,粒子运动的时间。
在电场中运动时qE=ma
(2023·江苏扬州市一模)如图所示,第一象限内存在垂直于纸面向里的匀强磁场;第四象限内存在沿+y轴的匀强电场,电场强度大小为E= 。t=0时刻,粒子从P点以速度v0平行+x轴射入电场,第1次通过x轴从Q点进入磁场。已知P点坐标为(0,-l),粒子质量为m、电荷量为+q,重力不计。
(1)求粒子经过Q点的速度v;
例2
粒子从P到Q做类平抛运动,轨迹如图甲所示,
解得α=45°
(2)欲使粒子不从y轴射出磁场,求磁感应强度的最小值Bm;
Q点到O点的距离s=2l,粒子进入磁场做匀速圆周运动,轨道半径为R,
欲使粒子不从y轴射出磁场,临界状态轨迹如图甲中圆弧部分
根据几何关系R+Rsin α=2l,
(3)若磁感应强度B= ,求粒子第5次通过x轴的位置x和时间t。
返回电场后做类斜抛运动,运动轨迹如图乙所示
总结提升
“5步”突破带电粒子在组合场中的运动问题
考点二
带电粒子在叠加场中的运动
1.三种典型情况
(1)若只有两个场,所受合力为零,则表现为匀速直线运动状态或静止状态。例如电场与磁场叠加满足qE=qvB时,重力场与磁场叠加满足mg=qvB时,重力场与电场叠加满足mg=qE时。
(2)若三场共存,所受合力为零时,粒子做匀速直线运动,其中洛伦兹力F=qvB的方向与速度v垂直。
2.分析
(2023·江苏卷·16)霍尔推进器某局部区域可抽象成如图所示的模型。Oxy平面内存在竖直向下的匀强电场和垂直坐标平面向里的匀强磁场,磁感应强度为B。质量为m、电荷量为e的电子从O点沿x轴正方向水平入射。入射速度为v0时,电子沿x轴做直线运动;入射速度小于v0时,电子的运动轨迹如图中的虚线所示,且在最高点与在最低点所受的合力大小相等。不计重力及电子间相互作用。
(1)求电场强度的大小E;
例3
答案 v0B
由题知,入射速度为v0时,电子沿x轴做直线运动,则有Ee=ev0B
解得E=v0B
(3)若电子入射速度在0
方法一 若电子以速度v入射时,设电子能到达的最高点位置的纵坐标为y,则根据动能定理有
由于电子在最高点与在最低点所受的合力大小相等,则在最高点有F合=evmB-eE
在最低点有F合=eE-evB
方法二 如果电子在复合场中受到的电场力与洛伦兹力等值反向,电子做匀速直线运动。如果这两个力不平衡,可将其分解为匀速直线运动和匀速圆周运动两个分运动。对于初状态静止的电子,设Ee=ev1B,可看作以v1=v0对应水平向右的匀速直线运动,而另一个分运动是v2=-v0,
设速度为v的电子,一个分运动为v1=v0,对应水平向右的匀速直线运动。另一个分运动的速度为v2,这个分运动做圆周运动的直径为y2,
电子入射速度为两个分速度的合速度,
在0
配速法其实就是给物体配一个速度v,使得这个速度所产生的洛伦兹力与题目中的重力或者电场力(视情况而定)抵消,对应的,还会出现一个与v等大反向的速度v′,此时等效为只受到一个洛伦兹力,而不再是重力或者电场力加上洛伦兹力,从而降低分析难度。
配速法
(1)求进入第1组磁场区的粒子的速度大小v;
答案 2v0
解得v=2v0
(2)调节磁场宽度,恰好使所有带电粒子都不能从第1组磁场的右边界穿出,求磁场的宽度Δx;
答案 d
粒子进入磁场时,速度方向与y轴负方向的夹角θ越小,粒子越容易射出磁场,θ的最小值为θ=60°
由几何关系可得Δx=R+Rcos θ
解得磁场的宽度Δx=d
设粒子在第n层磁场中运动的速度为vn,轨迹半径为rn(下标表示粒子所在组数),
1
2
3
4
1.如图所示,坐标系xOy的第一象限存在匀强磁场,磁场方向垂直于xOy平面向外;第四象限内有沿x轴负方向的匀强电场。质量为m、带电荷量为q(q>0)的粒子以速率v从y轴的点A(0, L)射入磁场,经x轴上的点C(L,0)沿y轴负方向进入电场,然后从y轴负半轴D点以与y轴负方向成60°角离开电场,不计粒子重力,求:
(1)粒子在A点时速度方向与y轴正方向的夹角θ;
答案 120°
1
2
3
4
根据题意,画出粒子的运动轨迹,如图所示
解得R=2L
由几何关系有θ=180°-(90°-∠OAO′)
解得θ=120°
1
2
3
4
(2)匀强电场的电场强度大小;
1
2
3
4
垂直电场方向上有y=vt2
1
2
3
4
(3)粒子在磁场和电场中运动的总时间t。
1
2
3
4
粒子在磁场和电场中运动的总时间
1
2
3
4
1
2
3
4
(1)求第一象限内所加电场的电场强度;
1
2
3
4
在第一象限内,电子做类平抛运动
根据牛顿第二定律得eE=ma
1
2
3
4
(2)若磁场充满第二象限,电子将从x轴上某点离开第二象限,求该点的坐标;
答案 (-2L,0)
1
2
3
4
根据几何关系可知x1=R+Rcos θ=2L
该点的坐标为(-2L,0)
1
2
3
4
(3)若磁场是一个圆形有界磁场,要使电子经磁场偏转后通过x轴时,与y轴负方向的夹角为30°,求圆形磁场区域的最小面积。
1
2
3
4
根据题意,作出轨迹图如图所示
1
2
3
4
3.如图所示,在竖直平面内x轴的上方空间内存在水平向右的匀强电场,x轴的下方空间内存在垂直纸面向外的匀强磁场和竖直向下的匀强电场,磁感应强度大小为0.3 T,电场强度大小均为1.2 V/m。一个带电小球用一根细线悬挂在x轴的上方区域,静止时细线与竖直方向夹角为θ=45°。现将细线剪断,小球运动1 s时第一次经过x轴进
入x轴下方区域。g取10 m/s2。求:(tan 63°≈2)
(1)小球第一次经过x轴时的速度大小;
1
2
3
4
静电力FE=qE=mgtan θ=mg,
1
2
3
4
将细线剪断后,小球在x轴上方做匀加速直线运动,小球的加速度大小为
1
2
3
4
(2)小球第三次经过x轴时的方向;
1
2
3
4
小球穿过x轴进入x轴下方后,由于小球所受重力mg和小球所受静电力FE等大反向,所以小球所受洛伦兹力为其合外力,小球将在此合外力下做匀速圆周运动。设小球第一次通过A点进入x轴下方,经过时间t2,在B点通过x轴,其第一次圆周运动轨迹示意图如图乙所示,
小球运动的圆弧轨迹对应的圆心角
洛伦兹力为其做圆周运动的向心力,有
1
2
3
4
小球在B点通过x轴,进入x轴上方,其速度方向与x轴上方复合场方向垂直,所以小球将做类平抛运动。设此过程小球运动时间为t3。小球将再次经过x轴,设此时其速度为v2,此过程运动轨迹示意图如丙所示,
1
2
3
4
1
2
3
4
(3)从剪断细线开始到小球第四次经过x轴的时间。
1
2
3
4
小球第三次经过x轴后,在x轴下方再次做匀速圆周运动,设此过程运动时间为t4,
1
2
3
4
4.(2022·江苏卷·15)某装置用电场控制带电粒子运动,工作原理如图所示,矩形ABCD区域内存在多层紧邻的匀强电场,每层的高度均为d,电场强度大小均为E,方向沿竖直方向交替变化,AB边长为12d,BC边长为8d,质量为m、电荷量为+q的粒子流从装置左端中点射入电场,粒子初动能为Ek,入射角为θ,在纸面内运动,不
计重力及粒子间的相互作用力。
(1)当θ=θ0时,若粒子能从CD边射出,
求该粒子通过电场的时间t;
答案 见解析
1
2
3
4
电场方向在竖直方向上,粒子所受静电力在竖直方向上,粒子在水平方向上做匀速直线运动,速度分解如图所示
粒子在水平方向的速度为vx=vcos θ0
1
2
3
4
(2)当Ek=4qEd时,若粒子从CD边射出电场时与轴线OO′的距离小于d,求入射角θ的范围;
答案 见解析
粒子进入电场后只有静电力做功,粒子在竖直方向上反复运动后,根据题意可知最终运动的空间如图所示,
若粒子从OO′上部分离开CD边,则静电力做负功,根据动能定理可知-qEx=Ek1-Ek
1
2
3
4
解得粒子在竖直方向上的最大位移为
xm=4dsin2 θ1
解得θ1<30°
1
2
3
4
1
2
3
4
答案 见解析
设粒子入射角为θ′时,粒子恰好从D点射出,由于粒子进入电场时,在水平方向做匀速直线运动,在竖直方向反复做加速度相同的减速运动,加速运动。粒子的速度
1
2
3
4
粒子在沿电场方向,反复做加速度相同的减速运动,加速运动,则
-2ad=v1d2-(v′sin θ′)2
2ad=v2d2-(v1d)2
-2ad=v3d2-(v2d)2
2ad=v4d2-(v3d)2
-2ad=v5d2-(v4d)2
2ad=v6d2-(v5d)2
则v2d=v4d=v6d=v′sin θ′
v1d=v3d=v5d
则粒子在分层电场中运动时间相等,设为t0,
1
2
3
4
1
2
3
4
代入数据化简可得6cos2θ′-8sin θ′cos θ′+1=0
即tan2θ′-8tan θ′+7=0
解得tan θ′=7(舍去)或tan θ′=1
1
2
3
4
则从CD边出射的粒子入射粒子的数量之比
同课章节目录
