5.3 三角形三边的关系(课件)-四年级下册数学人教版(共25张PPT)
文档属性
| 名称 | 5.3 三角形三边的关系(课件)-四年级下册数学人教版(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
三角形三边的关系
R·四年级下册
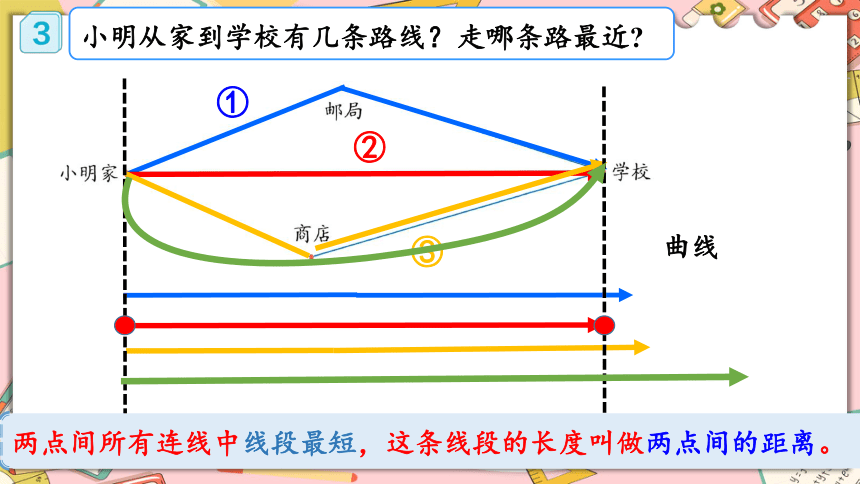
小明从家到学校有几条路线?
①
②
③
走哪条路最近
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
曲线
小明家、邮局、学校三地,连接后近似一个什么图形?
三角形是由三条线段首尾相接围成的平面图形。
三条线段一定能围成三角形吗?
什么样的3条线段能围成三角形呢?我们来做个实验。
剪出下面 4 组纸条(单位:cm)。
用每组纸条围三角形。
(1)6、7、8;
(2)4、5、9;
(3)3、6、10;
(4)8、11、11。
动手操作
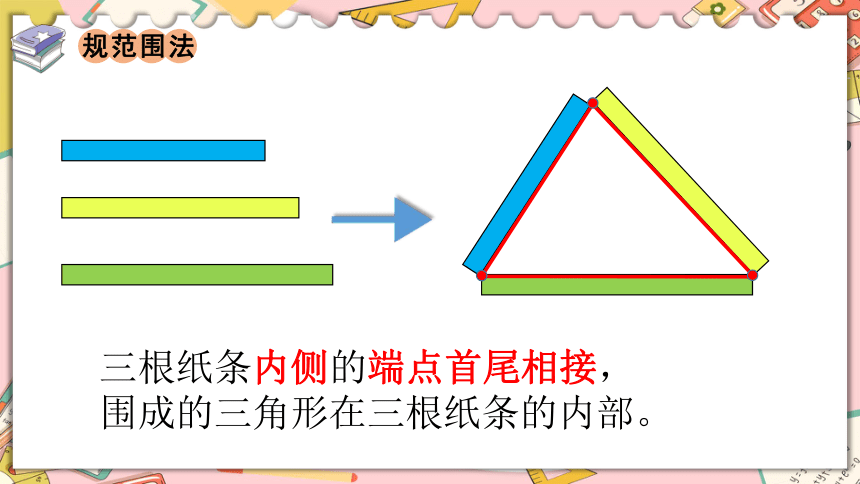
三根纸条内侧的端点首尾相接,
围成的三角形在三根纸条的内部。
规范围法
讨论:你发现了什么?
我也围成了一个三角形。
我也围成了一个三角形。
为什么?
并不是任意三个纸条都能围成一个三角形。
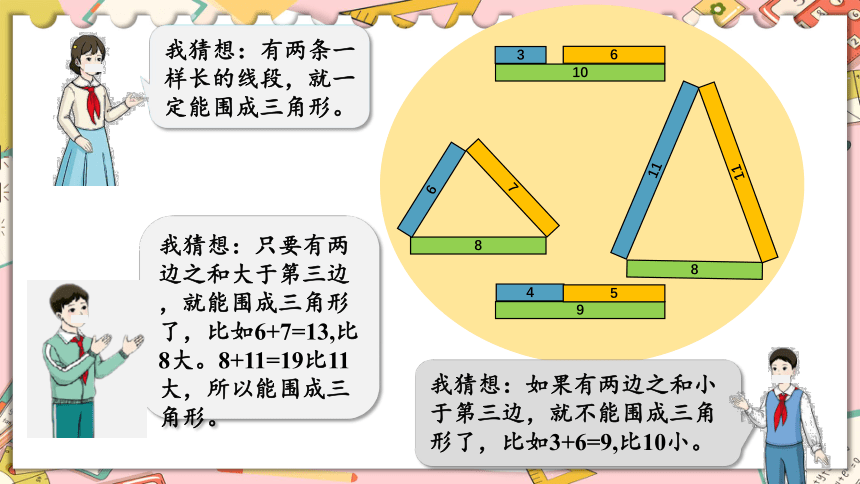
我猜想:有两条一样长的线段,就一定能围成三角形。
我猜想:如果有两边之和小于第三边,就不能围成三角形了,比如3+6=9,比10小。
我猜想:只要有两边之和大于第三边,就能围成三角形了,比如6+7=13,比8大。8+11=19比11大,所以能围成三角形。
10
3
6
9
4
5
8
6
7
8
11
11
活动要求:
先把数据记录在表格上,然后根据刚刚猜想,想一想、算一算三条边之间有怎样的关系 你发现了什么?
不能围成三角形
编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1)
(2)
发现
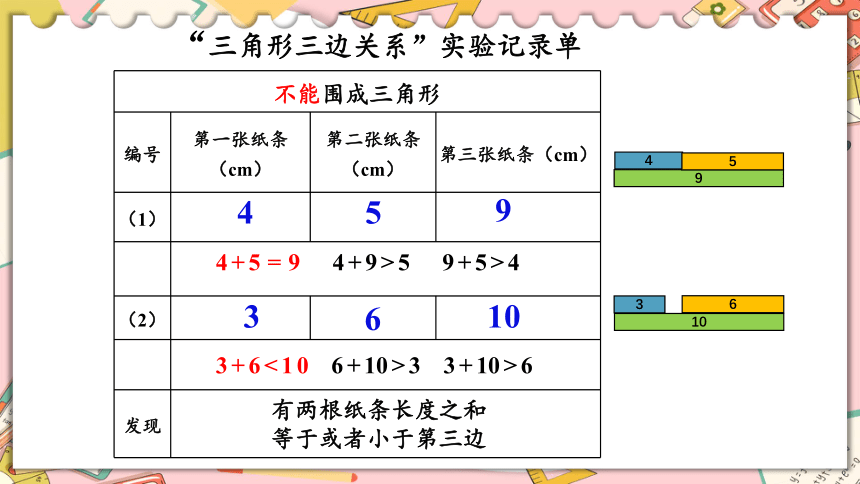
“三角形三边关系”实验记录单
4
5
9
3
6
10
4+5=9 4+9>5 9+5>4
3+6<10 6+10>3 3+10>6
10
3
6
9
4
5
有两根纸条长度之和
等于或者小于第三边
3
10
6
3
10
6
3
10
6
3+6<10
有两根纸条长度之和小于第三根
不能围成
3
10
6
4+6=10
有两根纸条长度之和等于第三根
不能围成
3
10
6
+1
我猜想:如果有两边之和小于第三边,就不能围成三角形了,比如3+6=9,比10小。
4
10
6
把4厘米纸条再延长一点儿。会不会围成三角形呢
10
6
能围成
两根纸条长度之和大于第三根
10
6
纸条最多延长到多长呢?
10
6
10
6
10
6
10
6
16
虽然16+10>6,
但是6+10=16。
不能围成
所以仅仅满足有两边之和大于第三边是不行的。
任意两根纸条长度之和都要大于第三根。
我猜想:只要有两边之和大于第三边,就能围成三角形了,比如6+7=13,比8大。8+11=19比11大,所以能围成三角形。
“三角形三边关系”实验记录单
能围成三角形
编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1)
(2)
发现
6
7
8
8
11
11
6+7>8
6+8>7
8+7>6
8+11>11
11+11>8
8
6
7
8
11
11
任意两根纸条长度之和大于第三边
三角形任意两条边
长度之和大于第三边。
小明从家到学校有几条路线?
①
②
③
走哪条路最近
因为三角形任意两边之和大于第三边,所以第二条路最近。
判断:下面小棒能不能围成三角形?( )
用两条最短边相加跟长边进行比较,最快。
练习
三角形任意两条边长度之和大于第三边。
10cm
4cm
4cm
4+4<10
我猜想:有两根条一样长的线段,就一定能围成三角形。
一个三角形的两条边分别是5厘米和10厘米,第三条边的长度(整厘米数)
最短是多少厘米?最长是多少厘米?
第三条边最短是:10-5+1=6(厘米)
第三条边最长是:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
三角形三边的关系可知: <第三边<
5<第三边<15
10
5
5
大一点
两边之差<第三边<两边之和
10
5
15
小一点
比
比
10-5
10+5
三角形三边的关系
2.三角形任意两边之和大于第三边。
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
3.判断3条线段能否围成三角形,只需要判断两条短边的和是否大于第三边,如果大于就能围成三角形,反之则不能。
4.三角形任意一条边的长度都小于另外两条边的长度和,都大于另外两条边的长度差。两边之差<第三边<两边之和
怎样将一根纸条两次剪成三段,让它们一定能围成
一个三角形
(1)第一次不能剪在哪里?为什么?
课后思考
(2)如果第一次剪在这里,第二次该剪在哪条线段上?
为什么?请动手剪一剪,验证能否围成三角形?
中点
中点
三角形三边的关系
R·四年级下册
小明从家到学校有几条路线?
①
②
③
走哪条路最近
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
曲线
小明家、邮局、学校三地,连接后近似一个什么图形?
三角形是由三条线段首尾相接围成的平面图形。
三条线段一定能围成三角形吗?
什么样的3条线段能围成三角形呢?我们来做个实验。
剪出下面 4 组纸条(单位:cm)。
用每组纸条围三角形。
(1)6、7、8;
(2)4、5、9;
(3)3、6、10;
(4)8、11、11。
动手操作
三根纸条内侧的端点首尾相接,
围成的三角形在三根纸条的内部。
规范围法
讨论:你发现了什么?
我也围成了一个三角形。
我也围成了一个三角形。
为什么?
并不是任意三个纸条都能围成一个三角形。
我猜想:有两条一样长的线段,就一定能围成三角形。
我猜想:如果有两边之和小于第三边,就不能围成三角形了,比如3+6=9,比10小。
我猜想:只要有两边之和大于第三边,就能围成三角形了,比如6+7=13,比8大。8+11=19比11大,所以能围成三角形。
10
3
6
9
4
5
8
6
7
8
11
11
活动要求:
先把数据记录在表格上,然后根据刚刚猜想,想一想、算一算三条边之间有怎样的关系 你发现了什么?
不能围成三角形
编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1)
(2)
发现
“三角形三边关系”实验记录单
4
5
9
3
6
10
4+5=9 4+9>5 9+5>4
3+6<10 6+10>3 3+10>6
10
3
6
9
4
5
有两根纸条长度之和
等于或者小于第三边
3
10
6
3
10
6
3
10
6
3+6<10
有两根纸条长度之和小于第三根
不能围成
3
10
6
4+6=10
有两根纸条长度之和等于第三根
不能围成
3
10
6
+1
我猜想:如果有两边之和小于第三边,就不能围成三角形了,比如3+6=9,比10小。
4
10
6
把4厘米纸条再延长一点儿。会不会围成三角形呢
10
6
能围成
两根纸条长度之和大于第三根
10
6
纸条最多延长到多长呢?
10
6
10
6
10
6
10
6
16
虽然16+10>6,
但是6+10=16。
不能围成
所以仅仅满足有两边之和大于第三边是不行的。
任意两根纸条长度之和都要大于第三根。
我猜想:只要有两边之和大于第三边,就能围成三角形了,比如6+7=13,比8大。8+11=19比11大,所以能围成三角形。
“三角形三边关系”实验记录单
能围成三角形
编号 第一张纸条(cm) 第二张纸条(cm) 第三张纸条(cm)
(1)
(2)
发现
6
7
8
8
11
11
6+7>8
6+8>7
8+7>6
8+11>11
11+11>8
8
6
7
8
11
11
任意两根纸条长度之和大于第三边
三角形任意两条边
长度之和大于第三边。
小明从家到学校有几条路线?
①
②
③
走哪条路最近
因为三角形任意两边之和大于第三边,所以第二条路最近。
判断:下面小棒能不能围成三角形?( )
用两条最短边相加跟长边进行比较,最快。
练习
三角形任意两条边长度之和大于第三边。
10cm
4cm
4cm
4+4<10
我猜想:有两根条一样长的线段,就一定能围成三角形。
一个三角形的两条边分别是5厘米和10厘米,第三条边的长度(整厘米数)
最短是多少厘米?最长是多少厘米?
第三条边最短是:10-5+1=6(厘米)
第三条边最长是:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
三角形三边的关系可知: <第三边<
5<第三边<15
10
5
5
大一点
两边之差<第三边<两边之和
10
5
15
小一点
比
比
10-5
10+5
三角形三边的关系
2.三角形任意两边之和大于第三边。
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
3.判断3条线段能否围成三角形,只需要判断两条短边的和是否大于第三边,如果大于就能围成三角形,反之则不能。
4.三角形任意一条边的长度都小于另外两条边的长度和,都大于另外两条边的长度差。两边之差<第三边<两边之和
怎样将一根纸条两次剪成三段,让它们一定能围成
一个三角形
(1)第一次不能剪在哪里?为什么?
课后思考
(2)如果第一次剪在这里,第二次该剪在哪条线段上?
为什么?请动手剪一剪,验证能否围成三角形?
中点
中点
