初中数学沪教版(五四学制)八年级数学下册试题 20.5一次函数的应用--行程问题(含解析)
文档属性
| 名称 | 初中数学沪教版(五四学制)八年级数学下册试题 20.5一次函数的应用--行程问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览



文档简介
20.5一次函数的应用--行程问题
一、选择题.
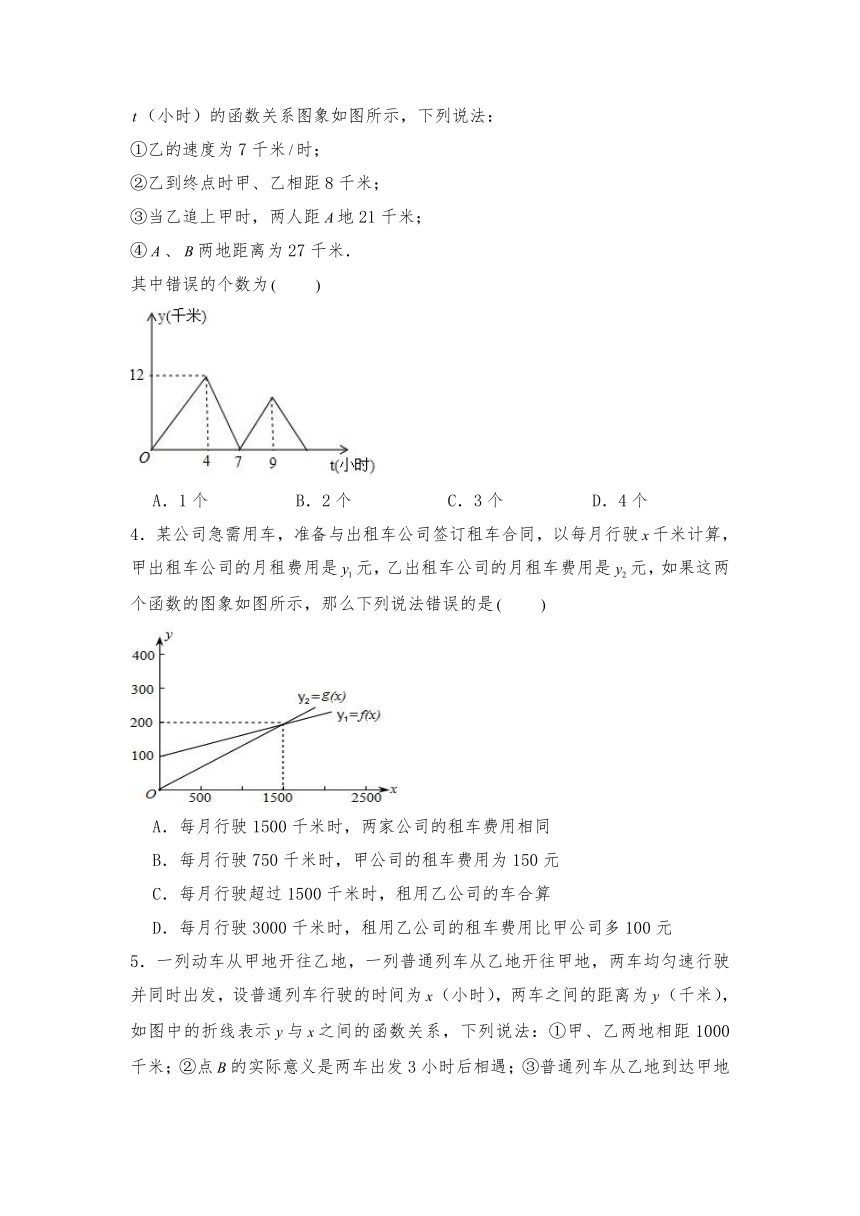
1.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段、分别反映了小张、小王步行所走的路程(千米)与时间(分钟)的函数关系,根据图象提供的信息,小王比小张早到乙地的时间是 分钟.
A.4 B.6 C.16 D.10
2.周末,小明骑自行车从家里出发去游玩.从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程与小明离家时间的函数图象,则下列说法中正确的是
A.小明在迪诺水镇游玩后,经过到达万达广场
B.小明的速度是,妈妈的速度是
C.万达广场离小明家
D.点的坐标为,
3.甲乙两人在同一条笔直的公路上步行从地去往地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图象如图所示,下列说法:
①乙的速度为7千米时;
②乙到终点时甲、乙相距8千米;
③当乙追上甲时,两人距地21千米;
④、两地距离为27千米.
其中错误的个数为
A.1个 B.2个 C.3个 D.4个
4.某公司急需用车,准备与出租车公司签订租车合同,以每月行驶千米计算,甲出租车公司的月租费用是元,乙出租车公司的月租车费用是元,如果这两个函数的图象如图所示,那么下列说法错误的是
A.每月行驶1500千米时,两家公司的租车费用相同
B.每月行驶750千米时,甲公司的租车费用为150元
C.每月行驶超过1500千米时,租用乙公司的车合算
D.每月行驶3000千米时,租用乙公司的租车费用比甲公司多100元
5.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为(小时),两车之间的距离为(千米),如图中的折线表示与之间的函数关系,下列说法:①甲、乙两地相距1000千米;②点的实际意义是两车出发3小时后相遇;③普通列车从乙地到达甲地时间是9小时;④动车的速度是270千米小时,其中不正确的有
A.4个 B.3个 C.2个 D.1个
6.甲、乙两人相约从地到地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到地后即停车等甲.甲、乙两人之间的距离(千米)与甲行驶的时间(小时)之间的函数关系如图所示,则乙从地到地所用的时间为
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
7.在、两地之间有汽车站在直线上),甲车由地驶往站,乙车由地驶往地,两车同时出发,匀速行驶,甲、乙两车离站的距离,(千米)与行驶时间(小时)之间的函数图象如图所示,则下列结论:
①、两地相距360千米;
②甲车速度比乙车速度快15千米时;
③乙车行驶11小时后到达地;
④两车行驶4.4小时后相遇.
其中正确的结论有
A.1 B.2个 C.3个 D.4个
8.甲、乙两人在直线跑道上同起点,同终点,同方向匀速跑200米,先到终点的人原地休息.已知甲先跑8米,乙才出发,在跑步过程中,甲、乙两人的距离(单位:米)与乙出发的时间(单位:秒)之间的关系如图所示,则图中的值是
A.44 B.46 C.48 D.50
9.在我国川西高原某山脉间有一河流,当河流中的水位上升到一定高度时因河堤承压有溃堤的危险.于是水利工程师在此河段的某处河堤上修了一个排水的预警水库联通另一支流.当河流的水位超过警戒位时就有河水流入预警的水库中,当水库有一定量的积水后,就会自动打开水库的排水系统流入另一支流.当河流的水位低于警戒位时水库的排水系统的排水速度则变慢.假设预警水库的积水时间为分钟,水库中积水量为吨,图中的折线表示某天与的函数关系,下列说法中:
①这天预警水库排水时间持续了80分钟;
②河流的水位超过警戒位时预警水库的排水速度比进水速度少25吨分;
③预警水库最高积水量为1500吨;
④河流的水位低于警戒位时预警水库的排水速度为30吨分.
其中正确的信息判断是
A.①④ B.①③ C.②③ D.②④
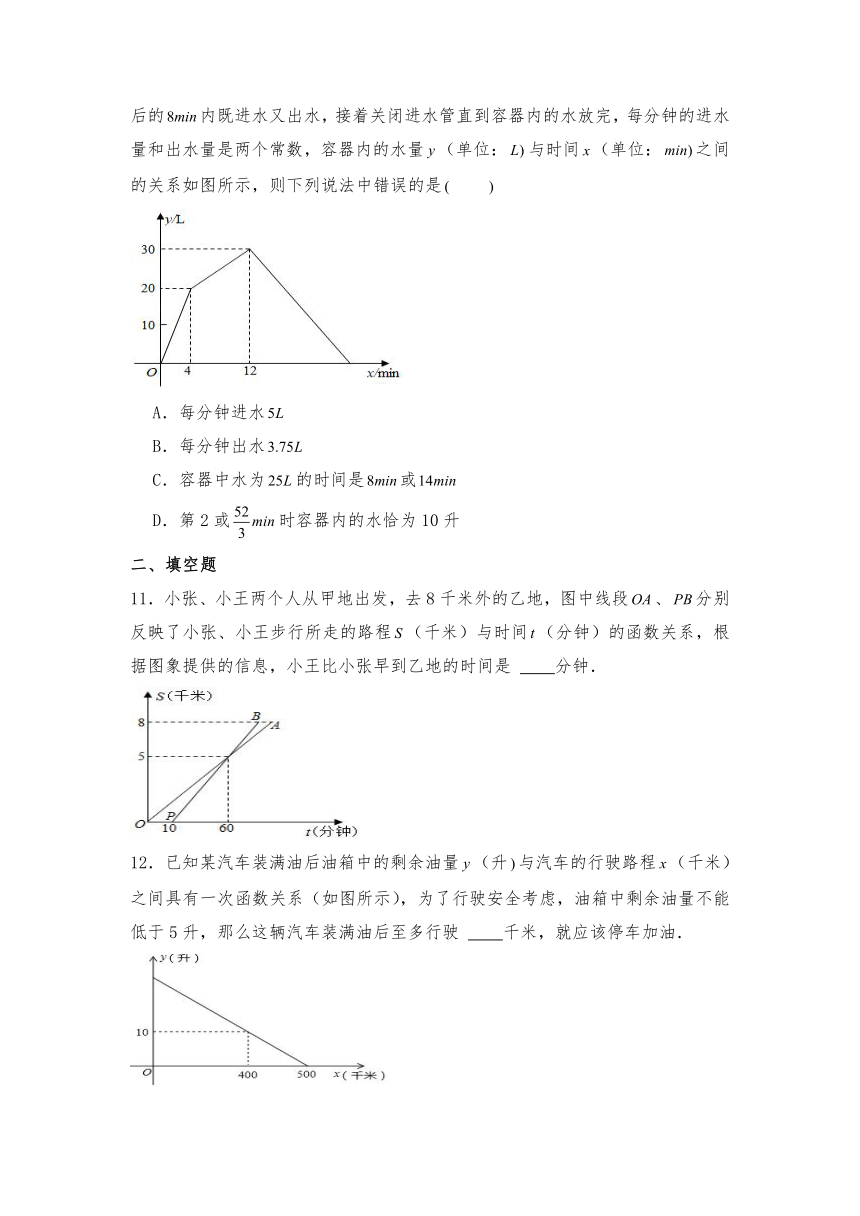
10.一个装有进水管和出水管的容器,从某时刻开始内只进水不出水,在随后的内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量(单位:与时间(单位:之间的关系如图所示,则下列说法中错误的是
A.每分钟进水
B.每分钟出水
C.容器中水为的时间是或
D.第2或时容器内的水恰为10升
二、填空题
11.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段、分别反映了小张、小王步行所走的路程(千米)与时间(分钟)的函数关系,根据图象提供的信息,小王比小张早到乙地的时间是 分钟.
12.已知某汽车装满油后油箱中的剩余油量(升与汽车的行驶路程(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,油箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶 千米,就应该停车加油.
13.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
14.已知某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)是一次函数关系,当汽车加满油后,行驶200千米,油箱中还剩油126升,行驶250千米,油箱中还剩油120升,那么当油箱中还剩油90升时,该汽车已行驶了 千米.
15.如图,、两地相距20千米,甲、乙两人都从地去地,图中和分别表示甲、乙两人所走路程(千米)与时间(小时)之间的关系,下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米小时;
④乙先到达地.
其中正确的是 (填序号).
16.尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福.当小艾同学到达敬老院时,发现拷音乐的盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来分钟后,爸爸在家找到了盘并立即前往敬老院,相遇后爸爸将盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离(米与小艾从敬老院出发的时间(分之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有 米.
17.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米时,两车之间的距离(千米)与货车行驶时间(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米时;
②图中点的坐标为,;
③甲、乙两地之间的距离为120千米;
④快递车从乙地返回时的速度为90千米时.
以上4个结论正确的是 .
18.一个阳光明媚的上午,小明和小兰相约从鲁能巴蜀中学沿相同的路线去龙头寺公园写生,小明出发5分钟后小兰才出发,此时小明发现忘记带颜料,立即按原速原路回学校拿颜料,小明拿到颜料后,以比原速提高的速度赶去公园,结果还是比小兰晚2分钟到公园(小明拿颜料的时间忽略不计).在整个过程中,小兰保持匀速运动,小明提速前后也分别保持匀速运动,如图所示是小明与小兰之间的距离(米与小明出发的时间(分钟)之间的函数图象,则学校到公园的距离为 米.
三、解答题
19.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则:
(1)A、B两城相距 千米;
(2)乙车速度为 千米/小时;
(3)乙车出发后 小时追上甲车.
20.、两地相距20千米,甲、乙两人某日中午12点同时从地出发匀速前往地,甲的速度是每小时4千米,如图,线段反映了乙所行的路程与所用时间之间的函数关系,根据提供的信息回答下列问题:
(1)乙由地前往地所行的路程与所用时间之间的函数解析式是 ,定义域是 ;
(2)在图中画出反映甲所行驶的路程与所用时间之间的函数图象;
(3)下午3点时,甲乙两人相距 千米.
21.有一辆货车在运输行驶过程中,油箱中的剩余油量(升与行驶路程(千米)之间是一次函数关系,如表列出了部分剩余油量(升与行驶路程(千米)的对应关系:
行驶路程(千米) 0 150 300
剩余油量(升 60 45 30
(1)求关于的函数关系式(不需要写定义域);
(2)已知当油箱中剩余油量为8升时,该汽车会开始提示加油,在此行驶过程中,行驶了500千米时,司机发现离前方最近的加油站还有25千米路程,在开往加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
22.某校八年级学生从学校出发,沿相同路线乘车前往崇明花博园游玩.已知1号车比2号车早20分钟出发,图4中、分别表示两车在行驶中的路程与时间的关系(图象不完整).
(1)求的函数表达式(不需写出定义域);
(2)如果2号车和1号车最终能同时到达,求汽车从学校到花博园行驶的路程.
23.甲、乙两名摩托车选手在匀速状态下进行赛道训练,已知两名选手先后从起点地驶往相距60千米的终点地.如果甲的速度比乙的速度慢1千米分钟,甲比乙早出发1分钟,最后乙先到达终点地,设甲的行驶时间为(分钟),甲、乙的行驶路程、(千米)与之间的函数图象如图所示.
(1)根据图象,回答问题:当乙到达终点地时, 千米;
(2)求甲、乙两名摩托车选手的速度;
(3)求关于的函数解析式.
24.小明和小杰从同一地点去青浦郊野公园,小明坐公交车去,小杰因为有事晚出发,乘出租车以1.6千米分钟的平均速度沿路追赶.图中,分别表示公交车与图象解决下列问题:
(1)小明早到了 分钟,公交车的平均速度为 千米分钟;
(2)小杰路上花费的时间是 分钟,比小明晚出发 分钟;
(3)求出租车行驶过程中与的函数关系式,并写出定义域.
答案
一、选择题.
1.【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【解析】由图象可知:
设的解析式为:,
经过点,
,
得,
函数解析式为:①,
把代入①得:,
解得:,
小张到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地的时间为小张出发后90(分钟),
小王比小张早到(分钟),
故选:.
2.【分析】根据题意和函数图象中的数据,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解析】由图象可得,
小明在迪诺水镇游玩后,经过到达万达广场,故选项错误;
小明的速度为,妈妈的速度是,故选项正确;
万达广场离小明家,故选项错误;
点的坐标为,,故选项错误;
故选:.
3.【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距地的距离;
④求出乙到达终点的路程就是,两地距离.
【解析】①由题意,得
甲的速度为:千米时;
设乙的速度为千米时,由题意,得
,
解得:.
即乙的速度为7千米时,
故①正确;
②乙到终点时甲、乙相距的距离为:
千米,故②正确;
③当乙追上甲时,两人距地距离为:
千米.故③正确;
④,两地距离为:
千米,故④错误.
综上所述:错误的只有④.
故选:.
4.【分析】根据图象看两个函数的交点所对应的自变量的取值是多少即可解答.
【解析】利用图象即可得出:,相交于,当时,的图象在的图象上方,当时,的图象在的图象上方,
.每月行驶1500千米时,两家公司的租车费用相同,正确,不符合题意;
.设关于的函数关系式为,
由题意得:,解得:,
,
每月行驶750千米时,甲公司的租车费用为(元,
每月行驶750千米时,甲公司的租车费用为150元,正确,不符合题意;
.每月行驶超过1500千米时,租用甲公司的车合算,故原说法错误,符合题意;
.设关于的函数关系式为,
由题意得:,解得:,
,
每月行驶3000千米时,,,
(元,
租用乙公司的租车费用比甲公司多100元,正确,不符合题意;
故选:.
5.【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解解:由图象可得,
甲、乙两地相距1000千米,
故①正确;
出发后3小时,两车之间的距离为0,
可知点的实际意义是两车出发后3小时相遇,
故②正确;
由图象可得,普通列车从乙地到达甲地时间是12小时,
故③不正确;
普通列车的速度是(千米小时),
设动车的速度为千米小时,
根据题意,得:,
解得:,
动车的速度为250千米小时,
故④不正确;
故选:.
6.【分析】根据速度路程时间,可求甲骑自行车的速度为千米小时,根据乙出发0.25小时追上甲,设乙速度为千米小时,列方程求出乙速度,设追上后到达地的时间是小时,根据追击路程列方程求解,再把两个时间相加即可求解.
【解析】由图像可得:甲骑自行车的速度为千米小时,乙出发0.25小时追上甲,
设乙速度为千米小时,
,
解得:,
乙速度为50千米小时,
设追上后到达地的时间是,
,
解得:,
乙从地到地所用的时间为(小时),
故选:.
7.【分析】利用图象信息以及速度,时间,路程之间的关系一一判断即可.
【解析】①、两地相距(千米),
故①错误,
②甲车的平均速度(千米小时),
乙车的平均速度(千米小时),
甲车速度比乙车速度快(千米小时),
故②错误,
③(小时),
乙车行驶11小时后到达地,故③正确,
④设小时相遇,则有:,
(小时),
两车行驶4.4小时后相遇,故④正确,
故选:.
8.【分析】乙的速度为(米秒),由追击问题可以求出甲的速度,即可得出结论.
【解析】由题意,得
乙的速度为:(米秒),
甲的速度为:(米秒),
(秒.
故选:.
9.【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否成立,从而可以解答本题.
【解析】由图象得:分,水库开始积水,
分,水库有一定量的积水,水库的排水系统打开,
分时,水库停止进水,只排水,
这天预警水库排水时间持续了分钟,故①错误;
(吨分),也就是水位超过警戒位时预警水库的排水速度比进水速度少25吨分,②正确;
从图象看出预警水库积水量为1500吨时停止进水,并不能反映出预警水库的最高积水量,③错误;
从图象看出河流的水位低于警戒位时预警水库的排水速度为(吨分),④正确.
故选:.
10.选:.
二、填空题
11.【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【解析】由图象可知:
设的解析式为:,
经过点,
,得,
函数解析式为:①,
把代入①得:,
解得:,
小张3到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地时间为小张出发后90(分钟),
小王比小张早到(分钟).
故答案为:6.
方法二:有图象可知,小王比小张先到时间为:
(分钟).
故答案为:6.
12.【分析】根据函数图象中点的坐标利用待定系数法求出一次函数解析式,再根据一次函数图象上点的坐标特征即可求出剩余油量为5升时行驶的路程,此题得解.
【解析】设该一次函数解析式为,
将、代入中,
,解得:,
该一次函数解析式为.
当时,.
故答案为:450
13.350.
14.【分析】根据题意,可以得到某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式,然后将代入函数解析式,求得相应的的值,即可解答本题.
【解析】设某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式是,
,得,
即某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式是,
当时,,得,
故答案为:500.
15.【分析】根据函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解析】由图象可得,
乙晚出发1小时,故①正确;
乙出发小时后追上甲,故②错误;
甲的速度是千米小时,故③正确;
乙先到达地,故④正确;
故答案为:①③④.
16.【分析】根据函数图象中的数据可知,在9分钟到11分钟小艾走的路程是180米,用时2分钟,从而可以求得此时的速度,即小艾提速后的速度,然后即可得到小艾开始的速度,再根据两人9分钟相遇,可以求得爸爸的速度,再根据题意和图象中的数据即可计算出当小艾回到敬老院时,爸爸离敬老院还有多少米.
【解析】由题意可得,
小艾的原来的速度为:(米分钟),
爸爸的速度为:(米分钟),
9分钟的时候,小艾离敬老院的距离为:(米,
小艾最后回到敬老院的时间为:(分钟),
当小艾回到敬老院时,爸爸离敬老院还有:(米,
故答案为:240.
17.【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解析】设快递车从甲地到乙地的速度为千米时,
,
解得,
即快递车从甲地到乙地的速度为100千米时,故①正确;
由已知可得,点的横坐标为:,纵坐标为:,
即点的坐标为,,故②正确;
甲乙两地之间的距离为(千米),故③错误;
设快递车从乙地返回时的速度为千米小时,
,
解得,故④正确;
故答案为:①②④.
18.【分析】根据题意和函数图象中的数据可以计算出小明提速后的速度和小兰的速度,然后设学校到公园的距离为米,即可得到相应的方程,从而可以解答本题.
【解析】由图象可得,
小明提速后的速度为:(米分钟),
小兰的速度为:(米分钟),
设学校到公园的距离为米,
,
解得,,
故答案为:720.
三、解答题
19.(1)由图象可得,A,B两城相距300千米,
故答案为:300;
(2)由图象可得,
乙车的速度为300÷(4﹣1)=100(千米/时),
故答案为:100;
(3)甲的速度为300÷5=60(千米/小时),
设乙车出发a小时追上甲车,
则60(a+1)=100a,
解得a=1.5,
即乙车出发1.5小时追上甲车.
故答案为:1.5.
20.(1)设直线的解析式为,且,
,解得;
;
由图象可知,;
故答案为:;;
(2)甲的速度是每小时4千米,
甲所用的时间(小时),
,
图象如下图所示:
(3)下午3点时,甲、乙两人之间的距离为:.
故答案为:2.
21.(1)设一次函数的关系式为,把,,代入得:
,
解得:,
一次函数的关系式为,
答:关于的函数关系式.
(2)当时,即,解得:,
即行驶520千米时,油箱的余油量为8升,
(千米),
答:在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是5千米.
22.(1)设的函数表达式为,把代入上式得
由题意得,
解得:,
;
(2)1号车的速度为,
设1号车出发分钟后到达花博园,则
,
解得,
故汽车从学校到花博园行驶的路程为(千米).
23.(1)观察图象知当乙到达终点地时,千米,
故答案为:52;
(2)设乙的速度是千米分钟,
由题意,得,
解得:,,
经检验,,是原方程的解,
,不合题意,舍去,
乙的速度是5千米分钟,甲的速度是4千米分钟;
(3)乙的行驶时间为(分钟),
设关于的函数解析式为,根据题意得,
,
解得,
关于的函数解析式为y=5x-5(1≤x≤13).
24.(1)根据图象可知,小明早到了:(分钟),
公交车的平均速度为:(千米分钟),
故答案为:5;1;
(2)小杰路上花费的时间是:(分钟),
小杰比小明晚出发:(分钟),
故答案为:25;20;
(3)由公交车的平均速度为1千米分钟,可得对应的表达式为;
设对应的表达式为,由题意得:
,
解得,
对应的表达式为s=1.6t-32(20≤t≤45).
一、选择题.
1.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段、分别反映了小张、小王步行所走的路程(千米)与时间(分钟)的函数关系,根据图象提供的信息,小王比小张早到乙地的时间是 分钟.
A.4 B.6 C.16 D.10
2.周末,小明骑自行车从家里出发去游玩.从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程与小明离家时间的函数图象,则下列说法中正确的是
A.小明在迪诺水镇游玩后,经过到达万达广场
B.小明的速度是,妈妈的速度是
C.万达广场离小明家
D.点的坐标为,
3.甲乙两人在同一条笔直的公路上步行从地去往地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图象如图所示,下列说法:
①乙的速度为7千米时;
②乙到终点时甲、乙相距8千米;
③当乙追上甲时,两人距地21千米;
④、两地距离为27千米.
其中错误的个数为
A.1个 B.2个 C.3个 D.4个
4.某公司急需用车,准备与出租车公司签订租车合同,以每月行驶千米计算,甲出租车公司的月租费用是元,乙出租车公司的月租车费用是元,如果这两个函数的图象如图所示,那么下列说法错误的是
A.每月行驶1500千米时,两家公司的租车费用相同
B.每月行驶750千米时,甲公司的租车费用为150元
C.每月行驶超过1500千米时,租用乙公司的车合算
D.每月行驶3000千米时,租用乙公司的租车费用比甲公司多100元
5.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为(小时),两车之间的距离为(千米),如图中的折线表示与之间的函数关系,下列说法:①甲、乙两地相距1000千米;②点的实际意义是两车出发3小时后相遇;③普通列车从乙地到达甲地时间是9小时;④动车的速度是270千米小时,其中不正确的有
A.4个 B.3个 C.2个 D.1个
6.甲、乙两人相约从地到地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到地后即停车等甲.甲、乙两人之间的距离(千米)与甲行驶的时间(小时)之间的函数关系如图所示,则乙从地到地所用的时间为
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
7.在、两地之间有汽车站在直线上),甲车由地驶往站,乙车由地驶往地,两车同时出发,匀速行驶,甲、乙两车离站的距离,(千米)与行驶时间(小时)之间的函数图象如图所示,则下列结论:
①、两地相距360千米;
②甲车速度比乙车速度快15千米时;
③乙车行驶11小时后到达地;
④两车行驶4.4小时后相遇.
其中正确的结论有
A.1 B.2个 C.3个 D.4个
8.甲、乙两人在直线跑道上同起点,同终点,同方向匀速跑200米,先到终点的人原地休息.已知甲先跑8米,乙才出发,在跑步过程中,甲、乙两人的距离(单位:米)与乙出发的时间(单位:秒)之间的关系如图所示,则图中的值是
A.44 B.46 C.48 D.50
9.在我国川西高原某山脉间有一河流,当河流中的水位上升到一定高度时因河堤承压有溃堤的危险.于是水利工程师在此河段的某处河堤上修了一个排水的预警水库联通另一支流.当河流的水位超过警戒位时就有河水流入预警的水库中,当水库有一定量的积水后,就会自动打开水库的排水系统流入另一支流.当河流的水位低于警戒位时水库的排水系统的排水速度则变慢.假设预警水库的积水时间为分钟,水库中积水量为吨,图中的折线表示某天与的函数关系,下列说法中:
①这天预警水库排水时间持续了80分钟;
②河流的水位超过警戒位时预警水库的排水速度比进水速度少25吨分;
③预警水库最高积水量为1500吨;
④河流的水位低于警戒位时预警水库的排水速度为30吨分.
其中正确的信息判断是
A.①④ B.①③ C.②③ D.②④
10.一个装有进水管和出水管的容器,从某时刻开始内只进水不出水,在随后的内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量(单位:与时间(单位:之间的关系如图所示,则下列说法中错误的是
A.每分钟进水
B.每分钟出水
C.容器中水为的时间是或
D.第2或时容器内的水恰为10升
二、填空题
11.小张、小王两个人从甲地出发,去8千米外的乙地,图中线段、分别反映了小张、小王步行所走的路程(千米)与时间(分钟)的函数关系,根据图象提供的信息,小王比小张早到乙地的时间是 分钟.
12.已知某汽车装满油后油箱中的剩余油量(升与汽车的行驶路程(千米)之间具有一次函数关系(如图所示),为了行驶安全考虑,油箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶 千米,就应该停车加油.
13.小明从家步行到学校需走的路程为1800米.图中的折线反映了小明从家步行到学校所走的路程(米与时间(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行 米.
14.已知某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)是一次函数关系,当汽车加满油后,行驶200千米,油箱中还剩油126升,行驶250千米,油箱中还剩油120升,那么当油箱中还剩油90升时,该汽车已行驶了 千米.
15.如图,、两地相距20千米,甲、乙两人都从地去地,图中和分别表示甲、乙两人所走路程(千米)与时间(小时)之间的关系,下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米小时;
④乙先到达地.
其中正确的是 (填序号).
16.尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福.当小艾同学到达敬老院时,发现拷音乐的盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来分钟后,爸爸在家找到了盘并立即前往敬老院,相遇后爸爸将盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离(米与小艾从敬老院出发的时间(分之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有 米.
17.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米时,两车之间的距离(千米)与货车行驶时间(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米时;
②图中点的坐标为,;
③甲、乙两地之间的距离为120千米;
④快递车从乙地返回时的速度为90千米时.
以上4个结论正确的是 .
18.一个阳光明媚的上午,小明和小兰相约从鲁能巴蜀中学沿相同的路线去龙头寺公园写生,小明出发5分钟后小兰才出发,此时小明发现忘记带颜料,立即按原速原路回学校拿颜料,小明拿到颜料后,以比原速提高的速度赶去公园,结果还是比小兰晚2分钟到公园(小明拿颜料的时间忽略不计).在整个过程中,小兰保持匀速运动,小明提速前后也分别保持匀速运动,如图所示是小明与小兰之间的距离(米与小明出发的时间(分钟)之间的函数图象,则学校到公园的距离为 米.
三、解答题
19.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则:
(1)A、B两城相距 千米;
(2)乙车速度为 千米/小时;
(3)乙车出发后 小时追上甲车.
20.、两地相距20千米,甲、乙两人某日中午12点同时从地出发匀速前往地,甲的速度是每小时4千米,如图,线段反映了乙所行的路程与所用时间之间的函数关系,根据提供的信息回答下列问题:
(1)乙由地前往地所行的路程与所用时间之间的函数解析式是 ,定义域是 ;
(2)在图中画出反映甲所行驶的路程与所用时间之间的函数图象;
(3)下午3点时,甲乙两人相距 千米.
21.有一辆货车在运输行驶过程中,油箱中的剩余油量(升与行驶路程(千米)之间是一次函数关系,如表列出了部分剩余油量(升与行驶路程(千米)的对应关系:
行驶路程(千米) 0 150 300
剩余油量(升 60 45 30
(1)求关于的函数关系式(不需要写定义域);
(2)已知当油箱中剩余油量为8升时,该汽车会开始提示加油,在此行驶过程中,行驶了500千米时,司机发现离前方最近的加油站还有25千米路程,在开往加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
22.某校八年级学生从学校出发,沿相同路线乘车前往崇明花博园游玩.已知1号车比2号车早20分钟出发,图4中、分别表示两车在行驶中的路程与时间的关系(图象不完整).
(1)求的函数表达式(不需写出定义域);
(2)如果2号车和1号车最终能同时到达,求汽车从学校到花博园行驶的路程.
23.甲、乙两名摩托车选手在匀速状态下进行赛道训练,已知两名选手先后从起点地驶往相距60千米的终点地.如果甲的速度比乙的速度慢1千米分钟,甲比乙早出发1分钟,最后乙先到达终点地,设甲的行驶时间为(分钟),甲、乙的行驶路程、(千米)与之间的函数图象如图所示.
(1)根据图象,回答问题:当乙到达终点地时, 千米;
(2)求甲、乙两名摩托车选手的速度;
(3)求关于的函数解析式.
24.小明和小杰从同一地点去青浦郊野公园,小明坐公交车去,小杰因为有事晚出发,乘出租车以1.6千米分钟的平均速度沿路追赶.图中,分别表示公交车与图象解决下列问题:
(1)小明早到了 分钟,公交车的平均速度为 千米分钟;
(2)小杰路上花费的时间是 分钟,比小明晚出发 分钟;
(3)求出租车行驶过程中与的函数关系式,并写出定义域.
答案
一、选择题.
1.【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【解析】由图象可知:
设的解析式为:,
经过点,
,
得,
函数解析式为:①,
把代入①得:,
解得:,
小张到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地的时间为小张出发后90(分钟),
小王比小张早到(分钟),
故选:.
2.【分析】根据题意和函数图象中的数据,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解析】由图象可得,
小明在迪诺水镇游玩后,经过到达万达广场,故选项错误;
小明的速度为,妈妈的速度是,故选项正确;
万达广场离小明家,故选项错误;
点的坐标为,,故选项错误;
故选:.
3.【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距地的距离;
④求出乙到达终点的路程就是,两地距离.
【解析】①由题意,得
甲的速度为:千米时;
设乙的速度为千米时,由题意,得
,
解得:.
即乙的速度为7千米时,
故①正确;
②乙到终点时甲、乙相距的距离为:
千米,故②正确;
③当乙追上甲时,两人距地距离为:
千米.故③正确;
④,两地距离为:
千米,故④错误.
综上所述:错误的只有④.
故选:.
4.【分析】根据图象看两个函数的交点所对应的自变量的取值是多少即可解答.
【解析】利用图象即可得出:,相交于,当时,的图象在的图象上方,当时,的图象在的图象上方,
.每月行驶1500千米时,两家公司的租车费用相同,正确,不符合题意;
.设关于的函数关系式为,
由题意得:,解得:,
,
每月行驶750千米时,甲公司的租车费用为(元,
每月行驶750千米时,甲公司的租车费用为150元,正确,不符合题意;
.每月行驶超过1500千米时,租用甲公司的车合算,故原说法错误,符合题意;
.设关于的函数关系式为,
由题意得:,解得:,
,
每月行驶3000千米时,,,
(元,
租用乙公司的租车费用比甲公司多100元,正确,不符合题意;
故选:.
5.【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解解:由图象可得,
甲、乙两地相距1000千米,
故①正确;
出发后3小时,两车之间的距离为0,
可知点的实际意义是两车出发后3小时相遇,
故②正确;
由图象可得,普通列车从乙地到达甲地时间是12小时,
故③不正确;
普通列车的速度是(千米小时),
设动车的速度为千米小时,
根据题意,得:,
解得:,
动车的速度为250千米小时,
故④不正确;
故选:.
6.【分析】根据速度路程时间,可求甲骑自行车的速度为千米小时,根据乙出发0.25小时追上甲,设乙速度为千米小时,列方程求出乙速度,设追上后到达地的时间是小时,根据追击路程列方程求解,再把两个时间相加即可求解.
【解析】由图像可得:甲骑自行车的速度为千米小时,乙出发0.25小时追上甲,
设乙速度为千米小时,
,
解得:,
乙速度为50千米小时,
设追上后到达地的时间是,
,
解得:,
乙从地到地所用的时间为(小时),
故选:.
7.【分析】利用图象信息以及速度,时间,路程之间的关系一一判断即可.
【解析】①、两地相距(千米),
故①错误,
②甲车的平均速度(千米小时),
乙车的平均速度(千米小时),
甲车速度比乙车速度快(千米小时),
故②错误,
③(小时),
乙车行驶11小时后到达地,故③正确,
④设小时相遇,则有:,
(小时),
两车行驶4.4小时后相遇,故④正确,
故选:.
8.【分析】乙的速度为(米秒),由追击问题可以求出甲的速度,即可得出结论.
【解析】由题意,得
乙的速度为:(米秒),
甲的速度为:(米秒),
(秒.
故选:.
9.【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否成立,从而可以解答本题.
【解析】由图象得:分,水库开始积水,
分,水库有一定量的积水,水库的排水系统打开,
分时,水库停止进水,只排水,
这天预警水库排水时间持续了分钟,故①错误;
(吨分),也就是水位超过警戒位时预警水库的排水速度比进水速度少25吨分,②正确;
从图象看出预警水库积水量为1500吨时停止进水,并不能反映出预警水库的最高积水量,③错误;
从图象看出河流的水位低于警戒位时预警水库的排水速度为(吨分),④正确.
故选:.
10.选:.
二、填空题
11.【分析】由函数图象求出、解析式,再把代入解析式就可以求出小张、小王所用时间.
【解析】由图象可知:
设的解析式为:,
经过点,
,得,
函数解析式为:①,
把代入①得:,
解得:,
小张3到达乙地所用时间为96(分钟);
设的解析式为:,
,
解得:,
的解析式为:②,
把代入②得:,
解得:,
则小王到达乙地时间为小张出发后90(分钟),
小王比小张早到(分钟).
故答案为:6.
方法二:有图象可知,小王比小张先到时间为:
(分钟).
故答案为:6.
12.【分析】根据函数图象中点的坐标利用待定系数法求出一次函数解析式,再根据一次函数图象上点的坐标特征即可求出剩余油量为5升时行驶的路程,此题得解.
【解析】设该一次函数解析式为,
将、代入中,
,解得:,
该一次函数解析式为.
当时,.
故答案为:450
13.350.
14.【分析】根据题意,可以得到某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式,然后将代入函数解析式,求得相应的的值,即可解答本题.
【解析】设某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式是,
,得,
即某汽车油箱中的剩余油量(升与该汽车行驶里程数(千米)函数关系式是,
当时,,得,
故答案为:500.
15.【分析】根据函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解析】由图象可得,
乙晚出发1小时,故①正确;
乙出发小时后追上甲,故②错误;
甲的速度是千米小时,故③正确;
乙先到达地,故④正确;
故答案为:①③④.
16.【分析】根据函数图象中的数据可知,在9分钟到11分钟小艾走的路程是180米,用时2分钟,从而可以求得此时的速度,即小艾提速后的速度,然后即可得到小艾开始的速度,再根据两人9分钟相遇,可以求得爸爸的速度,再根据题意和图象中的数据即可计算出当小艾回到敬老院时,爸爸离敬老院还有多少米.
【解析】由题意可得,
小艾的原来的速度为:(米分钟),
爸爸的速度为:(米分钟),
9分钟的时候,小艾离敬老院的距离为:(米,
小艾最后回到敬老院的时间为:(分钟),
当小艾回到敬老院时,爸爸离敬老院还有:(米,
故答案为:240.
17.【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解析】设快递车从甲地到乙地的速度为千米时,
,
解得,
即快递车从甲地到乙地的速度为100千米时,故①正确;
由已知可得,点的横坐标为:,纵坐标为:,
即点的坐标为,,故②正确;
甲乙两地之间的距离为(千米),故③错误;
设快递车从乙地返回时的速度为千米小时,
,
解得,故④正确;
故答案为:①②④.
18.【分析】根据题意和函数图象中的数据可以计算出小明提速后的速度和小兰的速度,然后设学校到公园的距离为米,即可得到相应的方程,从而可以解答本题.
【解析】由图象可得,
小明提速后的速度为:(米分钟),
小兰的速度为:(米分钟),
设学校到公园的距离为米,
,
解得,,
故答案为:720.
三、解答题
19.(1)由图象可得,A,B两城相距300千米,
故答案为:300;
(2)由图象可得,
乙车的速度为300÷(4﹣1)=100(千米/时),
故答案为:100;
(3)甲的速度为300÷5=60(千米/小时),
设乙车出发a小时追上甲车,
则60(a+1)=100a,
解得a=1.5,
即乙车出发1.5小时追上甲车.
故答案为:1.5.
20.(1)设直线的解析式为,且,
,解得;
;
由图象可知,;
故答案为:;;
(2)甲的速度是每小时4千米,
甲所用的时间(小时),
,
图象如下图所示:
(3)下午3点时,甲、乙两人之间的距离为:.
故答案为:2.
21.(1)设一次函数的关系式为,把,,代入得:
,
解得:,
一次函数的关系式为,
答:关于的函数关系式.
(2)当时,即,解得:,
即行驶520千米时,油箱的余油量为8升,
(千米),
答:在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是5千米.
22.(1)设的函数表达式为,把代入上式得
由题意得,
解得:,
;
(2)1号车的速度为,
设1号车出发分钟后到达花博园,则
,
解得,
故汽车从学校到花博园行驶的路程为(千米).
23.(1)观察图象知当乙到达终点地时,千米,
故答案为:52;
(2)设乙的速度是千米分钟,
由题意,得,
解得:,,
经检验,,是原方程的解,
,不合题意,舍去,
乙的速度是5千米分钟,甲的速度是4千米分钟;
(3)乙的行驶时间为(分钟),
设关于的函数解析式为,根据题意得,
,
解得,
关于的函数解析式为y=5x-5(1≤x≤13).
24.(1)根据图象可知,小明早到了:(分钟),
公交车的平均速度为:(千米分钟),
故答案为:5;1;
(2)小杰路上花费的时间是:(分钟),
小杰比小明晚出发:(分钟),
故答案为:25;20;
(3)由公交车的平均速度为1千米分钟,可得对应的表达式为;
设对应的表达式为,由题意得:
,
解得,
对应的表达式为s=1.6t-32(20≤t≤45).
