第六单元 第02课时 数的认识(二) (教学课件)六年级数学下册人教版(共55张PPT)
文档属性
| 名称 | 第六单元 第02课时 数的认识(二) (教学课件)六年级数学下册人教版(共55张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览








文档简介
(共55张PPT)
小学数学·六年级(下)·RJ
第2课时 总复习 数的认识(二)
2.复习整理整数和小数的相关知识,进一步理解数的意义、掌握数的读写、改写、大小比较,小数的性质、小数点移动的规律等知识。
使学生通过复习加深对整数、小数、分数和百分数的理解,进一步明确有关分数的意义和基本性质,体会整数与小数、小数与分数、分数与百分数的内在联系,完善认知结构。
使学生通过复习进一步感受数学学习的乐趣,发展学生对数学的积极情感,提高学好数学的信心。
进一步明确有关分数的意义和基本性质,体会整数与小数、小数与分数、分数与百分数的内在联系,完善认知结构。
复习整理整数和小数的相关知识,进一步理解数的意义、掌握数的读写、改写、大小比较,小数的性质、小数点移动规律等知识。
进一步发展数感,提高知识整理的能力。
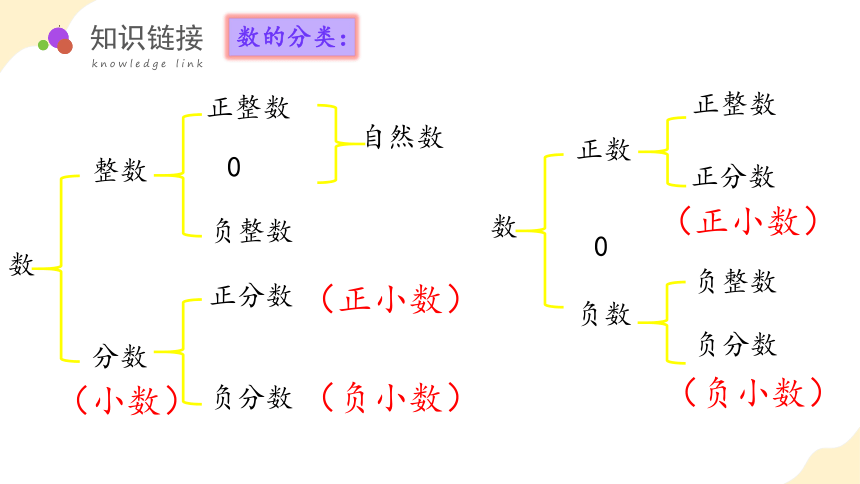
数的分类:
数
整数
正整数
负整数
0
分数
正分数
负分数
自然数
数
正数
正整数
正分数
负数
负整数
负分数
0
(小数)
(正小数)
(负小数)
(正小数)
(负小数)
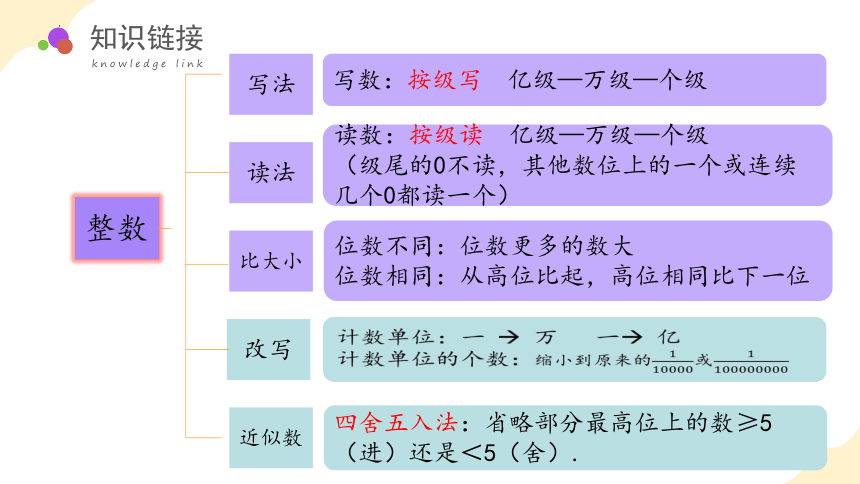
整数
写法
读法
比大小
改写
近似数
写数:按级写 亿级—万级—个级
读数:按级读 亿级—万级—个级
(级尾的0不读,其他数位上的一个或连续几个0都读一个)
位数不同:位数更多的数大
位数相同:从高位比起,高位相同比下一位
四舍五入法:省略部分最高位上的数≥5(进)还是<5(舍).
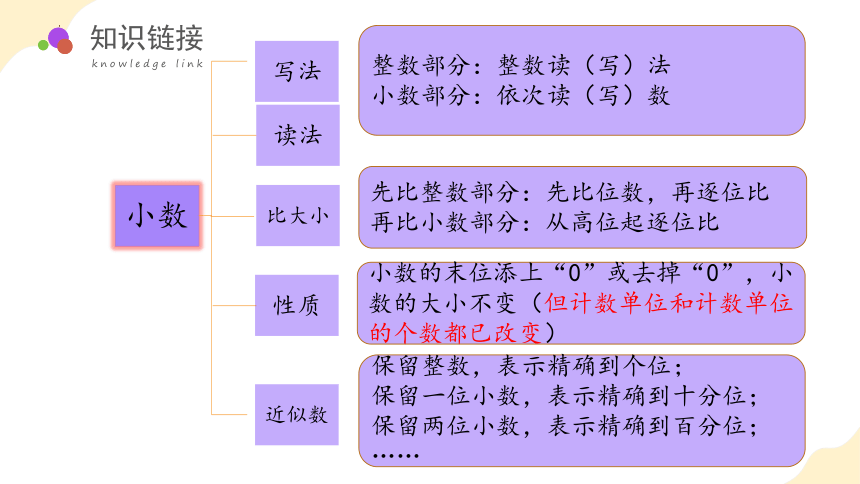
整数部分:整数读(写)法
小数部分:依次读(写)数
小数
写法
读法
比大小
性质
近似数
先比整数部分:先比位数,再逐位比
再比小数部分:从高位起逐位比
小数的末位添上“0”或去掉“0”,小数的大小不变(但计数单位和计数单位的个数都已改变)
保留整数,表示精确到个位;
保留一位小数,表示精确到十分位;
保留两位小数,表示精确到百分位;
……
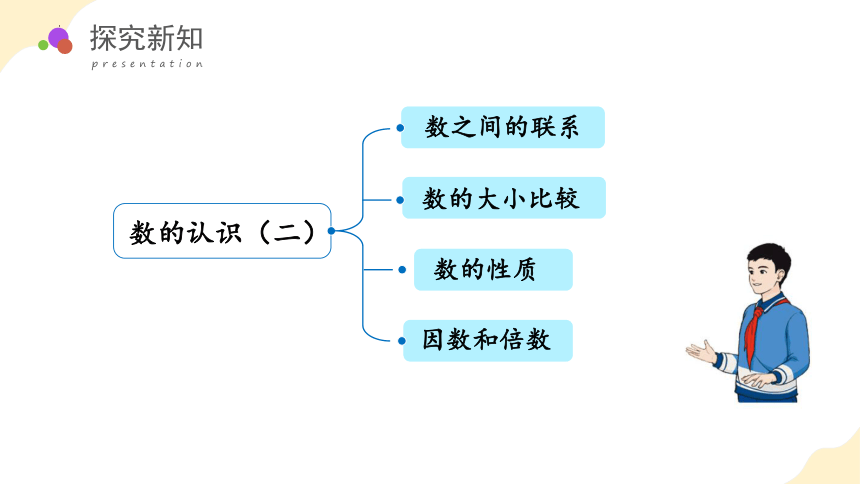
数之间的联系
数的认识(二)
因数和倍数
数的大小比较
数的性质
回顾和整理数和数之间的关系,会比较数的大小,构建数的认识的知识网络。
数之间的联系
整数与分数
整数(0除外)可以看作分母是1的分数。
……
1
1
1=
2
1
2=
3
1
3=
整数与分数
假分数中分子是分母的倍数的数都能化成整数。
整数(0除外)可以化成指定分母的假分数。
……
6
3
2=
20
4
5=
63
9
7=
4
2
=
2
1
6
3
=
8
4
=
=2
整数与小数
小数部分是0的小数可以改写成整数的形式。
整数可以改写成小数的形式。
2=2.0=2.00……
15.00=15……
分数与百分数的区别和联系
区别
分数可以表示一个数值,也可以表示两个数的比。
百分数只表示一个数占另一个数的百分比,不能表示具体的数值。
75%只能表示3是4的75%。
可以表示具体的数值 ,也可以表示3是4的 。
3
4
3
4
3
4
分数与百分数的区别和联系
区别
分数后面可以带单位名称。
百分数后面不能带单位名称。
dm
3
4
75%dm
百分数在原来的分子后面加“%”表示
分数写成的 形式。
a
b
3
4
75%
×
分数与百分数的区别和联系
联系
百分数是一种特殊的分数。
百分数的分母是100,但不能说分母是100的数就是百分数。
小数、分数和百分数
分数
百分数
小数
分子除以分母
先把小数改写成分母是
10、100、1000……的分数,
再化简
先把分数化成小数,
再把小数化成百分数
先把百分数化成分母
是100的分数,再化简
把小数点向左移动两位,去掉百分号
把小数点向右移动两位,加上百分号
数的大小比较
整数的大小比较
3211500 997899
>
793639999 793640001
<
先看它们的位数,如果位数不同,那么位数多的数就大;
如果位数相同,就从最高位比起,最高位上的数字大的那个数就大;
如果最高位上的数字相同,就比较下一位……以此类推,直到比较出两个数的大小为止。
小数的大小比较
3.5 2.99
>
2.469 2.471
<
先看它们的整数部分,整数部分大的那个数就大;
如果整数部分相同,十分位上的数字大的那个数就大;
如果十分位上的数字相同,百分位上的数字大的那个数就大……以此类推,直到比较出两个数的大小为止。
分数的大小比较
>
2
3
1
3
3
5
3
7
5
7
4
5
>
<
分母相同,分子大的分数大;
分子相同,分母小的分数大。
分子和分母都不相同,先通分,化成同分母分数,再比较大小。
百分数的大小比较
35.4% 35%
>
0.9% 1.1%
<
分母都是100,百分号前面的数大的百分数就大
复习整理数的性质,因数和倍数的相关知识。
你能根据a÷b=c(a、b、c均为整数,且b≠0)说明因数与倍数的含义吗?
这个问题需要我们进行归纳整理的知识有:整除,因数与倍数,质数与合数,能被2、5、3整除的数的特征。
因数和倍数
因数和倍数
a×b=c
因数和倍数的意义
c是a和b的倍数。
a和b是c的因数;
因数和倍数是相互依存的,二者不能单独存在。
(a、b、c都是正整数)
因数和倍数
因数和倍数的特征
一个数的因数的个数是( )的;
最小的因数是( );
最大的因数是( )。
一个数的倍数的个数是( )的;
最小的倍数是( );
( )最大的倍数。
有限
1
它本身
无限
它本身
没有
2、5、3的倍数的特征
2的倍数的特征:
5的倍数的特征:
3的倍数的特征:
2和5的倍数的特征:
个位上是0的数
个位上是0、2、4、6、8的数
个位上是0或5的数
一个数各个数位上的数字之和是3的倍数
奇数和偶数
在自然数中,最小的奇数是( );最小的偶数是( )。
按是否是2的倍数分类:
自然数
奇数
偶数
(是2的倍数的数)
(不是2的倍数的数)
1
0
奇数和偶数的意义
个位是1、3、5、7、9的数。
个位是0、2、4、6、8的数。
奇数和偶数
奇数和偶数的性质
偶数+偶数=偶数
偶数-偶数=偶数
偶数×偶数=偶数
奇数+奇数=偶数
奇数-奇数=偶数
奇数×奇数=奇数
偶数+奇数=奇数
偶数-奇数=奇数
偶数×奇数=偶数
质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫做质数(素数)。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
最小的质数是( ),( )最大的质数。
最小的合数是( ),( )最大的合数。
( )既不是质数,也不是合数。
2
没有
4
没有
1
问
什么是质数?什么是合数?
质数和合数
写出20以内的质数和合数。
质数:2、3、5、7、11、13、
17、19
合数:4、6、8、9、10、12、
14、15、16、18、20
按因数的个数分类:
自然数
1
合数
质数
(0除外)
最大公因数和最小公倍数
公因数和最大公因数的意义
12的因数
20的因数
20的因数
12和20的公因数
12和20的最大公因数是( )。
12的因数
1,
2,
4,
6,
3,
12
1,
2,
4,
5,
10,
20
3,
6,
12
1,
2,
4
5,
10,
20
4
最大公因数和最小公倍数
求最大公因数的方法
求18和27的最大公因数。
18的因数:1 ,2 ,3 ,6 ,9 ,18
27的因数:1 ,3 ,9 ,27
18和27的公因数:1 ,3 ,9
最大公因数
列举法
最大公因数和最小公倍数
求最大公因数的方法
求18和27的最大公因数。
筛选法
18的因数:1 ,2 ,3 ,6 ,9 ,18
1×27=27
3×9=27
9×3=27
18和27的公因数:1 ,3 ,9
最大公因数
最大公因数和最小公倍数
公倍数和最小公倍数的意义
6的倍数
9的倍数
9的倍数
6和9的公倍数
6和9的最小公倍数是( )。
6的倍数
6,
12,
24,
30,
…
18,
36,
9,
18,
27,
36,
45,
54,
…
6,
12,
24,
30,
…
18,
36,
…
9,
27,
45,
54,
…
18
最大公因数和最小公倍数
求最小公倍数的方法
求6和8的最小公倍数。
6的倍数:6,12,18,24,30,36 ,42,48,…
8的倍数:8,16,24,32,40,48,…
6和8的公倍数:24 ,48 ,…
最小公倍数
列举法
最大公因数和最小公倍数
求最小公倍数的方法
求6和8的最小公倍数。
6的倍数:6,12,18,24,30,36 ,42,48,…
8×3=24
8×6=48
6和8的公倍数:24,48,…
最小公倍数
筛选法
最大公因数和最小公倍数
一个数的因数是有限的,两个数的公因数也是有限的,其中最小的公因数是1。
一个数的倍数是无限的,两个数的公倍数也是无限的,没有最大的公倍数。
如果较小数是较大数的因数,那么较小数就是这两个数的最大公因数,较大数就是这两个数的最小公倍数;
如果两个数只有公因数1,那么它们的最大公因数是1,最小公倍数是这两个数的积。
最大公因数和最小公倍数
4和8的最大公因数是( ),最小公倍数是( )。
3和5的最大公因数是( ),最小公倍数是( )。
4
8
1
15
移动小数点的位置,小数的大小会发生什么变化?
小数的性质
小数的末尾添上“0”或去掉“0”,小数的大小不变。
分数的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
小数的性质与分数的基本性质的联系
小数的性质和分数的基本性质是一致的。
小数的性质
分数的基本性质
10
100
=
1
10
100
1000
=
……
0.10
=
0.1
0.100
=
……
小数点位置移动引起小数大小变化的规律
小数点向右移动一位、两位、三位……该数就扩大到原来的( )倍、 ( )倍、 ( )倍……
小数点向左移动一位、两位、三位……该数就缩小到原来的( )、 ( )、 ( )……
1
100
1
10
1
1000
10
100
1000
你能举例说明1万有多大、1亿有多大吗?
我们学校有1千人,十个这样的学校就是1万人。
1亿是比较大的数,一亿张纸的厚度比珠穆朗玛峰还高;
一亿粒大米,可以让3.5万人填饱肚子;
一亿个小学生手拉手可绕地球赤道一圈。
达标练习,巩固成果
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
(2)这些两位数中,哪些是质数 哪些是合数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
(4)这些两位数中,2和3的公倍数有 ,3和5的公倍数是 。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
答:12个
按照演绎:第一位上摆上4个数字中的任意一个有4种情况,第二位不能与第一位是同一个数字,那么剩下3个数字选一个有3种发展分支,4、3相乘为12;
例举:23、24、25、32、34、35、42、43、45、52、53、54共12个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(2)这些两位数中,哪些是质数 哪些是合数
答:质数:23、43、53共3个。
合数:24、25、32、34、35、42、45、52、54共9个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
答:2的倍数:24、32、34、42、52、54共6个。
3的倍数是:24、42、45、54共4个。
5的倍数是:25、35、45共3个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
(2)这些两位数中,哪些是质数 哪些是合数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
(4)这些两位数中,2和3的公倍数有 ,3和5的公倍数是 。
24、42、54
45
2.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。 ( )
(2)0是正数。 ( )
(3)假分数的倒数一定都是真分数。 ( )
(4)所有的偶数都是合数。 ( )
(5)a(a为整数,a>1)的所有因数都小于a。 ( )
√
×
×
×
×
3.断下面的说法是否正确。
(1)0.9,0,99, 0.999,( ),……,这列数越来越大,越来越接近( )。
(2) , , , , ,( ),……,这列数越来越小,越来越接近( )。
0.9999
1
0
4.比较 、 、 、 、的大小,你能发现什么?根据你发现的规律猜一下 和 哪个更大,并设法验证。
我发现分母比分子多1时,分母越大这个分数越大。
>
>
>
>
5.一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个
答:这箱苹果的数量应该是8和10的最小公倍数多6的数。
8和10的最小公倍数是40。
40+6=46(个)
答:这箱苹果的数量应该是46个。
6.把下面四个数按照从小到大的顺序排列起来。
3
1
0.30
30%
0.03
0.30
=0.303030…
30%
=0.30
3
1
=0.333333…
0.03<0.3<0.303030…<0.333333…
<
3
1
0.30
30%
0.03
<
<
7.王老师买来一些水果糖和棒棒糖分别平均分给一个组的同学,都正好分完。这个组最多可能有几位同学?每人得到几块水果糖,几块棒棒糖?
45块
30块
45和30的最大公因数是15。
答:这个组最多可能有15 位同学,每人得到3块水果糖、2块棒棒糖。
45 ÷ 15 = 3(块)
30 ÷ 15 = 2(块)
8.某公共汽车站是5路车和9路车的始发站,从早上6:00同时各发出第一辆车后,5路车每15分钟发一辆,9路车每18分钟发一辆。下次两路车同时发车是在什么时刻?
15和18的最小公倍数是3×5×6=90
90分=1时30分
6时+1时30分=7时30分
答:下次两路车同时发车是在7:30。
这节课你有什么收获?
对学习过的数进行了整理
复习了有关整数和小数的知识
小学数学·六年级(下)·RJ
第2课时 总复习 数的认识(二)
2.复习整理整数和小数的相关知识,进一步理解数的意义、掌握数的读写、改写、大小比较,小数的性质、小数点移动的规律等知识。
使学生通过复习加深对整数、小数、分数和百分数的理解,进一步明确有关分数的意义和基本性质,体会整数与小数、小数与分数、分数与百分数的内在联系,完善认知结构。
使学生通过复习进一步感受数学学习的乐趣,发展学生对数学的积极情感,提高学好数学的信心。
进一步明确有关分数的意义和基本性质,体会整数与小数、小数与分数、分数与百分数的内在联系,完善认知结构。
复习整理整数和小数的相关知识,进一步理解数的意义、掌握数的读写、改写、大小比较,小数的性质、小数点移动规律等知识。
进一步发展数感,提高知识整理的能力。
数的分类:
数
整数
正整数
负整数
0
分数
正分数
负分数
自然数
数
正数
正整数
正分数
负数
负整数
负分数
0
(小数)
(正小数)
(负小数)
(正小数)
(负小数)
整数
写法
读法
比大小
改写
近似数
写数:按级写 亿级—万级—个级
读数:按级读 亿级—万级—个级
(级尾的0不读,其他数位上的一个或连续几个0都读一个)
位数不同:位数更多的数大
位数相同:从高位比起,高位相同比下一位
四舍五入法:省略部分最高位上的数≥5(进)还是<5(舍).
整数部分:整数读(写)法
小数部分:依次读(写)数
小数
写法
读法
比大小
性质
近似数
先比整数部分:先比位数,再逐位比
再比小数部分:从高位起逐位比
小数的末位添上“0”或去掉“0”,小数的大小不变(但计数单位和计数单位的个数都已改变)
保留整数,表示精确到个位;
保留一位小数,表示精确到十分位;
保留两位小数,表示精确到百分位;
……
数之间的联系
数的认识(二)
因数和倍数
数的大小比较
数的性质
回顾和整理数和数之间的关系,会比较数的大小,构建数的认识的知识网络。
数之间的联系
整数与分数
整数(0除外)可以看作分母是1的分数。
……
1
1
1=
2
1
2=
3
1
3=
整数与分数
假分数中分子是分母的倍数的数都能化成整数。
整数(0除外)可以化成指定分母的假分数。
……
6
3
2=
20
4
5=
63
9
7=
4
2
=
2
1
6
3
=
8
4
=
=2
整数与小数
小数部分是0的小数可以改写成整数的形式。
整数可以改写成小数的形式。
2=2.0=2.00……
15.00=15……
分数与百分数的区别和联系
区别
分数可以表示一个数值,也可以表示两个数的比。
百分数只表示一个数占另一个数的百分比,不能表示具体的数值。
75%只能表示3是4的75%。
可以表示具体的数值 ,也可以表示3是4的 。
3
4
3
4
3
4
分数与百分数的区别和联系
区别
分数后面可以带单位名称。
百分数后面不能带单位名称。
dm
3
4
75%dm
百分数在原来的分子后面加“%”表示
分数写成的 形式。
a
b
3
4
75%
×
分数与百分数的区别和联系
联系
百分数是一种特殊的分数。
百分数的分母是100,但不能说分母是100的数就是百分数。
小数、分数和百分数
分数
百分数
小数
分子除以分母
先把小数改写成分母是
10、100、1000……的分数,
再化简
先把分数化成小数,
再把小数化成百分数
先把百分数化成分母
是100的分数,再化简
把小数点向左移动两位,去掉百分号
把小数点向右移动两位,加上百分号
数的大小比较
整数的大小比较
3211500 997899
>
793639999 793640001
<
先看它们的位数,如果位数不同,那么位数多的数就大;
如果位数相同,就从最高位比起,最高位上的数字大的那个数就大;
如果最高位上的数字相同,就比较下一位……以此类推,直到比较出两个数的大小为止。
小数的大小比较
3.5 2.99
>
2.469 2.471
<
先看它们的整数部分,整数部分大的那个数就大;
如果整数部分相同,十分位上的数字大的那个数就大;
如果十分位上的数字相同,百分位上的数字大的那个数就大……以此类推,直到比较出两个数的大小为止。
分数的大小比较
>
2
3
1
3
3
5
3
7
5
7
4
5
>
<
分母相同,分子大的分数大;
分子相同,分母小的分数大。
分子和分母都不相同,先通分,化成同分母分数,再比较大小。
百分数的大小比较
35.4% 35%
>
0.9% 1.1%
<
分母都是100,百分号前面的数大的百分数就大
复习整理数的性质,因数和倍数的相关知识。
你能根据a÷b=c(a、b、c均为整数,且b≠0)说明因数与倍数的含义吗?
这个问题需要我们进行归纳整理的知识有:整除,因数与倍数,质数与合数,能被2、5、3整除的数的特征。
因数和倍数
因数和倍数
a×b=c
因数和倍数的意义
c是a和b的倍数。
a和b是c的因数;
因数和倍数是相互依存的,二者不能单独存在。
(a、b、c都是正整数)
因数和倍数
因数和倍数的特征
一个数的因数的个数是( )的;
最小的因数是( );
最大的因数是( )。
一个数的倍数的个数是( )的;
最小的倍数是( );
( )最大的倍数。
有限
1
它本身
无限
它本身
没有
2、5、3的倍数的特征
2的倍数的特征:
5的倍数的特征:
3的倍数的特征:
2和5的倍数的特征:
个位上是0的数
个位上是0、2、4、6、8的数
个位上是0或5的数
一个数各个数位上的数字之和是3的倍数
奇数和偶数
在自然数中,最小的奇数是( );最小的偶数是( )。
按是否是2的倍数分类:
自然数
奇数
偶数
(是2的倍数的数)
(不是2的倍数的数)
1
0
奇数和偶数的意义
个位是1、3、5、7、9的数。
个位是0、2、4、6、8的数。
奇数和偶数
奇数和偶数的性质
偶数+偶数=偶数
偶数-偶数=偶数
偶数×偶数=偶数
奇数+奇数=偶数
奇数-奇数=偶数
奇数×奇数=奇数
偶数+奇数=奇数
偶数-奇数=奇数
偶数×奇数=偶数
质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫做质数(素数)。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
最小的质数是( ),( )最大的质数。
最小的合数是( ),( )最大的合数。
( )既不是质数,也不是合数。
2
没有
4
没有
1
问
什么是质数?什么是合数?
质数和合数
写出20以内的质数和合数。
质数:2、3、5、7、11、13、
17、19
合数:4、6、8、9、10、12、
14、15、16、18、20
按因数的个数分类:
自然数
1
合数
质数
(0除外)
最大公因数和最小公倍数
公因数和最大公因数的意义
12的因数
20的因数
20的因数
12和20的公因数
12和20的最大公因数是( )。
12的因数
1,
2,
4,
6,
3,
12
1,
2,
4,
5,
10,
20
3,
6,
12
1,
2,
4
5,
10,
20
4
最大公因数和最小公倍数
求最大公因数的方法
求18和27的最大公因数。
18的因数:1 ,2 ,3 ,6 ,9 ,18
27的因数:1 ,3 ,9 ,27
18和27的公因数:1 ,3 ,9
最大公因数
列举法
最大公因数和最小公倍数
求最大公因数的方法
求18和27的最大公因数。
筛选法
18的因数:1 ,2 ,3 ,6 ,9 ,18
1×27=27
3×9=27
9×3=27
18和27的公因数:1 ,3 ,9
最大公因数
最大公因数和最小公倍数
公倍数和最小公倍数的意义
6的倍数
9的倍数
9的倍数
6和9的公倍数
6和9的最小公倍数是( )。
6的倍数
6,
12,
24,
30,
…
18,
36,
9,
18,
27,
36,
45,
54,
…
6,
12,
24,
30,
…
18,
36,
…
9,
27,
45,
54,
…
18
最大公因数和最小公倍数
求最小公倍数的方法
求6和8的最小公倍数。
6的倍数:6,12,18,24,30,36 ,42,48,…
8的倍数:8,16,24,32,40,48,…
6和8的公倍数:24 ,48 ,…
最小公倍数
列举法
最大公因数和最小公倍数
求最小公倍数的方法
求6和8的最小公倍数。
6的倍数:6,12,18,24,30,36 ,42,48,…
8×3=24
8×6=48
6和8的公倍数:24,48,…
最小公倍数
筛选法
最大公因数和最小公倍数
一个数的因数是有限的,两个数的公因数也是有限的,其中最小的公因数是1。
一个数的倍数是无限的,两个数的公倍数也是无限的,没有最大的公倍数。
如果较小数是较大数的因数,那么较小数就是这两个数的最大公因数,较大数就是这两个数的最小公倍数;
如果两个数只有公因数1,那么它们的最大公因数是1,最小公倍数是这两个数的积。
最大公因数和最小公倍数
4和8的最大公因数是( ),最小公倍数是( )。
3和5的最大公因数是( ),最小公倍数是( )。
4
8
1
15
移动小数点的位置,小数的大小会发生什么变化?
小数的性质
小数的末尾添上“0”或去掉“0”,小数的大小不变。
分数的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
小数的性质与分数的基本性质的联系
小数的性质和分数的基本性质是一致的。
小数的性质
分数的基本性质
10
100
=
1
10
100
1000
=
……
0.10
=
0.1
0.100
=
……
小数点位置移动引起小数大小变化的规律
小数点向右移动一位、两位、三位……该数就扩大到原来的( )倍、 ( )倍、 ( )倍……
小数点向左移动一位、两位、三位……该数就缩小到原来的( )、 ( )、 ( )……
1
100
1
10
1
1000
10
100
1000
你能举例说明1万有多大、1亿有多大吗?
我们学校有1千人,十个这样的学校就是1万人。
1亿是比较大的数,一亿张纸的厚度比珠穆朗玛峰还高;
一亿粒大米,可以让3.5万人填饱肚子;
一亿个小学生手拉手可绕地球赤道一圈。
达标练习,巩固成果
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
(2)这些两位数中,哪些是质数 哪些是合数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
(4)这些两位数中,2和3的公倍数有 ,3和5的公倍数是 。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
答:12个
按照演绎:第一位上摆上4个数字中的任意一个有4种情况,第二位不能与第一位是同一个数字,那么剩下3个数字选一个有3种发展分支,4、3相乘为12;
例举:23、24、25、32、34、35、42、43、45、52、53、54共12个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(2)这些两位数中,哪些是质数 哪些是合数
答:质数:23、43、53共3个。
合数:24、25、32、34、35、42、45、52、54共9个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
答:2的倍数:24、32、34、42、52、54共6个。
3的倍数是:24、42、45、54共4个。
5的倍数是:25、35、45共3个。
1.数字 2、3、4、5 能组成多少个没有重复数字的两位数
(1)这些两位数中,哪些是奇数 哪些是偶数
(2)这些两位数中,哪些是质数 哪些是合数
(3)这些两位数中,哪些是2的倍数 哪些是 3的倍数 哪些是5的倍数
(4)这些两位数中,2和3的公倍数有 ,3和5的公倍数是 。
24、42、54
45
2.判断下面的说法是否正确,并说一说你的理由。
(1)把0.56扩大到它的100倍是560。 ( )
(2)0是正数。 ( )
(3)假分数的倒数一定都是真分数。 ( )
(4)所有的偶数都是合数。 ( )
(5)a(a为整数,a>1)的所有因数都小于a。 ( )
√
×
×
×
×
3.断下面的说法是否正确。
(1)0.9,0,99, 0.999,( ),……,这列数越来越大,越来越接近( )。
(2) , , , , ,( ),……,这列数越来越小,越来越接近( )。
0.9999
1
0
4.比较 、 、 、 、的大小,你能发现什么?根据你发现的规律猜一下 和 哪个更大,并设法验证。
我发现分母比分子多1时,分母越大这个分数越大。
>
>
>
>
5.一箱苹果,如果每8个装一盒,还剩余6个;如果每10个装一盒,也剩余6个。这箱苹果至少有多少个
答:这箱苹果的数量应该是8和10的最小公倍数多6的数。
8和10的最小公倍数是40。
40+6=46(个)
答:这箱苹果的数量应该是46个。
6.把下面四个数按照从小到大的顺序排列起来。
3
1
0.30
30%
0.03
0.30
=0.303030…
30%
=0.30
3
1
=0.333333…
0.03<0.3<0.303030…<0.333333…
<
3
1
0.30
30%
0.03
<
<
7.王老师买来一些水果糖和棒棒糖分别平均分给一个组的同学,都正好分完。这个组最多可能有几位同学?每人得到几块水果糖,几块棒棒糖?
45块
30块
45和30的最大公因数是15。
答:这个组最多可能有15 位同学,每人得到3块水果糖、2块棒棒糖。
45 ÷ 15 = 3(块)
30 ÷ 15 = 2(块)
8.某公共汽车站是5路车和9路车的始发站,从早上6:00同时各发出第一辆车后,5路车每15分钟发一辆,9路车每18分钟发一辆。下次两路车同时发车是在什么时刻?
15和18的最小公倍数是3×5×6=90
90分=1时30分
6时+1时30分=7时30分
答:下次两路车同时发车是在7:30。
这节课你有什么收获?
对学习过的数进行了整理
复习了有关整数和小数的知识
