八年级数学下册试题 第20章一次函数单元测试(培优提升卷)-沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第20章一次函数单元测试(培优提升卷)-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 08:33:10 | ||
图片预览



文档简介
第20章一次函数单元测试(培优提升卷)
一、选择题.
1.以下函数中,属于一次函数的是
A. B. C. D.
2.直线的图象经过
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
3.一次函数的图象不经过第四象限,那么的取值范围是
A. B. C.k≥3 D.k≤3
4.直线的截距是
A.1 B. C.2 D.
5.直线与坐标轴交于、两点,点在坐标轴上,为等腰三角形,则满足条件的点最多有
A.8 B.4 C.5 D.7
6.已知直线经过第一、二、四象限,那么直线一定不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.一次函数的图象如图所示,当时,的取值范围是
A. B. C. D.
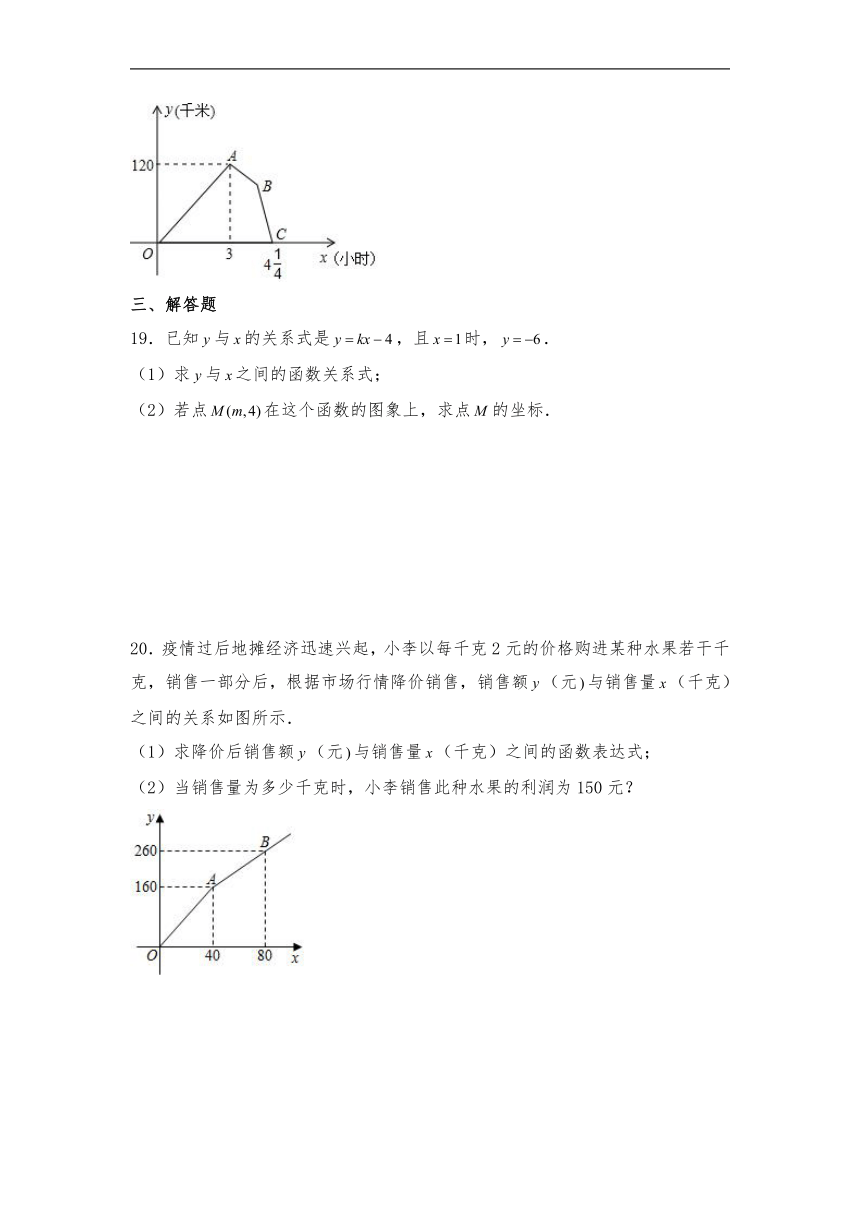
8.甲乙两人在同一条笔直的公路上步行从地去往地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图象如图所示,下列说法:
①乙的速度为7千米时;
②乙到终点时甲、乙相距8千米;
③当乙追上甲时,两人距地21千米;
④、两地距离为27千米.
其中错误的个数为
A.1个 B.2个 C.3个 D.4个
9.如图,甲、丙两地相距,一列快车从甲地驶往丙地,途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线表示两车之间的距离与慢车行驶的时间之间的函数关系.根据图中提供的信息,下列说法不正确的是
A.甲、乙两地之间的距离为
B.快车从甲地驶到丙地共用了
C.快车速度是慢车速度的1.5倍
D.快车到达丙地时,慢车距丙地还有
10.如图,正比例函数与一次函数的图象交于点.下面四个结论:①;②;③不等式的解集是;④当时,.其中正确的是
A.①② B.②③ C.①④ D.①③
二、填空题
11.直线沿轴向上平移3个单位得到的直线表达式是 .
12.已知一次函数,若的值随的增大而增大,则的取值范围是 .
13.将直线沿轴方向向上平移3个单位,所得新图象的函数表达式是 .
14.已知一次函数的图象经过点与,那么关于的不等式的解集是 .
15.已知点和点在函数的图象上,那 (填“”、“ ”或“” .
16.已知一次函数,当时,总有,则的取值范围为 .
17.一次函数的图象上有一点,将点向右平移1个单位,再向下平移2个单位得到点,若点也在该函数的图象上,则 .
18.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米时,两车之间的距离(千米)与货车行驶时间(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米时;
②图中点的坐标为,;
③甲、乙两地之间的距离为120千米;
④快递车从乙地返回时的速度为90千米时.
以上4个结论正确的是 .
三、解答题
19.已知与的关系式是,且时,.
(1)求与之间的函数关系式;
(2)若点在这个函数的图象上,求点的坐标.
20.疫情过后地摊经济迅速兴起,小李以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额(元与销售量(千克)之间的关系如图所示.
(1)求降价后销售额(元与销售量(千克)之间的函数表达式;
(2)当销售量为多少千克时,小李销售此种水果的利润为150元?
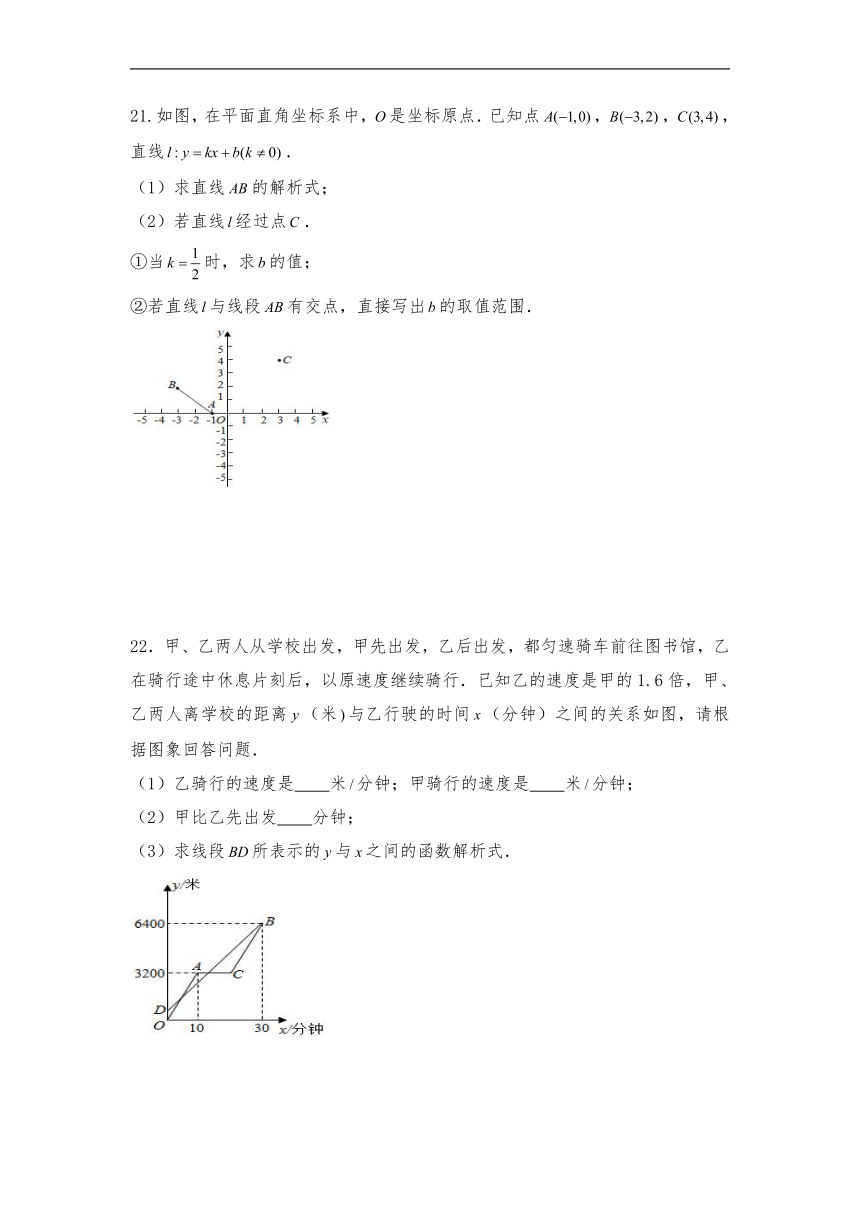
21.如图,在平面直角坐标系中,是坐标原点.已知点,,,直线.
(1)求直线的解析式;
(2)若直线经过点.
①当时,求的值;
②若直线与线段有交点,直接写出的取值范围.
22.甲、乙两人从学校出发,甲先出发,乙后出发,都匀速骑车前往图书馆,乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍,甲、乙两人离学校的距离(米与乙行驶的时间(分钟)之间的关系如图,请根据图象回答问题.
(1)乙骑行的速度是 米分钟;甲骑行的速度是 米分钟;
(2)甲比乙先出发 分钟;
(3)求线段所表示的与之间的函数解析式.
23.已知一次函数的图象经过点,两点.
(1)求一次函数的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求这个一次函数与坐标轴围成的三角形面积.
24.今年初,很多商场由于受新型冠状病毒肺炎疫情的影响,产品销售情况不如人意.有甲、乙两家商场利用网络平台进行销售.其中甲商场所有商品按9折出售,乙商场对一次购物中超过200元后的金额打折为1到9之间的整数).设顾客所购商品原来金额为元,在甲、乙两家商场实际支付金额分别为元和元.
(1)顾客在乙商场购物时,与之间函数图象如图所示(图中线段和射线,求当时,与之间函数解析式;
(2)当时,甲、乙两个商场中,去哪商场购物更省钱?
25.随着我国防疫形势进一步好转,各景区陆续开始对游客开放,某景区对团体门票采用灵活的售票方法,设团体人数为人,非节假日购票款为(元,节假日购票款为(元,、与之间的函数图象如图所示.
(1)非节假日门票定价是 元人;
(2)当时,与之间的函数关系式 ;
(3)某导游于10月1日(节假日)带团,10月12日(非节假日)带团到该景区,共付门票款1900元,、两个团队游客合计50人(且两团游客人数均超过15人).求:、两个团队游客各有多少人?
26.对于平面直角坐标系内的点和点,若点能绕着点旋转之后,落在轴上,则称是的转换点.
(1)已知点.
①如图,在,,中,是的转换点的是 ;
②是点的转换点,则的取值范围是 ;
(2)已知直线上所有点都是的转换点,直接写出的取值范围.
答案
一、选择题.
1.【分析】根据一次函数定义:形如,、是常数)的函数,叫做一次函数进行分析即可.
【解析】、是一次函数,故此选项符合题意;
、,当时是一次函数,故此选项不符合题意;
、不是一次函数,右边不是整式,故此选项不符合题意;
、不是一次函数,的指数为2,故此选项不符合题意;
故选:.
2.【分析】由直线的解析式,利用一次函数图象与系数的关系,可得出直线的图象经过的象限,此题得解.
【解析】,,
直线的图象经过第一、三、四象限.
故选:.
3.【分析】根据一次函数的性质即可求解.
【解析】一次函数的图象不经过第四象限,
,
解得,
故选:.
4.【分析】代入求出与之对应的值,此题得解.
【解析】当时,,
直线的截距为.
故选:.
5.【分析】运用分类讨论的数学思想,分为腰或底两种情况来分类解析,逐一判断,即可解决问题.
【解析】如图,对于直线,
当时,;
当时,,
直线与两个坐标轴的交点分别为,;
若以点为圆心,以的长为半径画弧,
则与轴有两个交点,与轴有一个交点(点除外);
若以点为圆心,以的长为半径画弧,
则与轴有一个交点(点除外),与轴有两个交点;
以为腰的等腰有6个;
若以为底,作的垂直平分线,与坐标轴交于原点,
综上所述,满足条件的点最多有7个,
故选:.
6.【分析】由直线经过一、二、四象限可分析,,由此判定不经过第二象限.
【解析】直线经过第一、二、四象限,
,,
直线一定不经过第二象限.
故选:.
7.【分析】根据图象的性质,当即图象在轴右方,.
【解析】根据图象和数据可知,当即图象在轴右方,.
故选:.
8.【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距地的距离;
④求出乙到达终点的路程就是,两地距离.
【解析】①由题意,得
甲的速度为:千米时;
设乙的速度为千米时,由题意,得
,
解得:.
即乙的速度为7千米时,
故①正确;
②乙到终点时甲、乙相距的距离为:
千米,故②正确;
③当乙追上甲时,两人距地距离为:
千米.故③正确;
④,两地距离为:
千米,故④错误.
综上所述:错误的只有④.
故选:.
9.【分析】.因为两车同时出发,同向而行,所以点就是甲、乙两地之间的距离为;
.由点为两车的路程差,相遇时间为2小时,可知:快车速度慢车速度,再由点可知慢车从乙地到达丙地;由此求出慢车速度,进一步求出快车速度,进而得出快车从甲地驶到丙地所用时间;
.通过求出列出的速度判断即可;
.根据“路程速度时间”即可.
【解析】点,
甲、乙两地之间的距离为,故说法正确,不符合题意;
点纵坐标为,即快慢两车的距离为0,
点表示时,快车追上慢车,
慢车速度:,快车速度:,
快车速度是慢车速度的1.5倍;故说法正确,不符合题意;
快车速度是,
快车从甲地驶到丙地共用了,故说法错误,符合题意;
两车同时出发,同向而行,
慢车距丙地的距离为:,故说法正确,不符合题意;
故选:.
10.【分析】根据正比例函数和一次函数的性质判断即可.
【解析】因为正比例函数经过二、四象限,所以,①正确;
一次函数经过一、二、三象限,所以,②错误;
由图象可得:不等式的解集是,③正确;
当时,,④错误;
故选:.
二、填空题
11.【分析】根据“上加下减”的原则进行解答即可.
【解析】直线沿轴向上平移3个单位得到的直线表达式是:,即.
故答案是:.
12.【分析】根据一次函数图象与系数的关系可判断.
【解析】一次函数一次函数中,的值随的增大而增大,
,
故答案是:.
13.【分析】根据“上加下减”的原则进行解答即可.
【解析】由“上加下减”的原则可知,将直线沿轴方向向上平移3个单位所得函数的解析式为,即.
故答案为:.
14.【分析】首先利用图象可找到图象在轴上方时,进而得到关于的不等式的解集是.
【解析】由题意可得:一次函数中,时,图象在轴上方,,
则关于的不等式的解集是,
故答案是:.
15.【分析】分别将和代入,表示出、,作差即可比较其大小.
【解析】点和点在函数的图象上,
,,
,
,
故答案为:.
16.【分析】分及两种情况考虑,利用一次函数的性质及一次函数图象上点的坐标特征,即可得出关于的一元一次不等式,解之即可得出结论.
【解析】当时,随的增大而增大,
,解得:,
;
当时,随的增大而减小,
,解得:,
.
故答案为:或.
17.【分析】根据平移的特性写出点的坐标,由点、均在一次函数的图象上,代入解得即可.
【解析】点的坐标为,则点的坐标为,
依题意得:,
解得:,
故答案为:0.
18.【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解析】设快递车从甲地到乙地的速度为千米时,
,
解得,
即快递车从甲地到乙地的速度为100千米时,故①正确;
由已知可得,点的横坐标为:,纵坐标为:,
即点的坐标为,,故②正确;
甲乙两地之间的距离为(千米),故③错误;
设快递车从乙地返回时的速度为千米小时,
,
解得,故④正确;
故答案为:①②④.
三、解答题
19.(1)与的函数关系是,
把,代入得:,
解得:.
则与函数关系式为;
(2)把点代入,
得:,
解得,
所以点的坐标是.
20.(1)设降价后销售额(元与销售量(千克)之间的函数表达式是,
段过点,,
,
解得,,
即降价后销售额(元与销售量(千克)之间的函数表达式是;
(2)设当销售量为千克时,小李销售此种水果的利润为150元,
,
解得,,
答:当销售量为180千克时,小李销售此种水果的利润为150元.
21.(1)设直线的解析式为,把点,代入得:
,解得:,
直线的解析式为;
(2)①把,代入得:
,解得:,
的值为;
②把代入得,即,
把点代入得:,解得:,
把点代入得:,解得:,
的取值范围为:1≤b≤3.
22.(1)由图象可得,
乙骑行的速度为:(米分钟),
甲骑行的速度为:(米分钟),
故答案为:320,200;
(2)甲从学校到图书馆的时间为:(分钟),
甲比乙先出发(分钟),
故答案为:2;
(3)点的纵坐标为:,
故点的坐标为,点的坐标为,
设线段所表示的与之间的函数解析式是,
,
解得,
即线段所表示的与之间的函数解析式是y=200x+400(0≤x≤300).
23.(1)一次函数的图象经过两点、,
,
函数解析式为:;
(2)函数图象如图
;
(3)一次函数与轴的交点为,
的面积.
24.(1)设当时,与之间函数解析式为,
由图象得,,
解得:,
当时,与之间函数解析式为;
(2)当时,
甲商场实际支付金额为(元,
乙商场实际支付金额为(元,
所以当时,去乙商场购物更省钱.
25.(1)由图象可得与之间为正比例函数,时,,
(元,
故答案为:30;
(2)当时,设,
函数图象经过点和,
,
,
,
故答案为:;
(3)设团有人,表示出团的人数为人,
当时,,
解得,
(人,
答:团有25人,团有25人.
26.(1)①,,.
,,.
的转换点的是,.
②如图,点轨迹为直线.
.
当时解得.
或.
(2)如图,作直线于点.直线交轴轴于点,.
,,.
.
即.
由题意得到直线距离到轴距离,即 ≥,
①t≥0时,0≤t≤3.
②时,-≤t<0.
③t≤-2时无解.
故答案为:-≤t≤3.
一、选择题.
1.以下函数中,属于一次函数的是
A. B. C. D.
2.直线的图象经过
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
3.一次函数的图象不经过第四象限,那么的取值范围是
A. B. C.k≥3 D.k≤3
4.直线的截距是
A.1 B. C.2 D.
5.直线与坐标轴交于、两点,点在坐标轴上,为等腰三角形,则满足条件的点最多有
A.8 B.4 C.5 D.7
6.已知直线经过第一、二、四象限,那么直线一定不经过
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.一次函数的图象如图所示,当时,的取值范围是
A. B. C. D.
8.甲乙两人在同一条笔直的公路上步行从地去往地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图象如图所示,下列说法:
①乙的速度为7千米时;
②乙到终点时甲、乙相距8千米;
③当乙追上甲时,两人距地21千米;
④、两地距离为27千米.
其中错误的个数为
A.1个 B.2个 C.3个 D.4个
9.如图,甲、丙两地相距,一列快车从甲地驶往丙地,途中经过乙地,一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线表示两车之间的距离与慢车行驶的时间之间的函数关系.根据图中提供的信息,下列说法不正确的是
A.甲、乙两地之间的距离为
B.快车从甲地驶到丙地共用了
C.快车速度是慢车速度的1.5倍
D.快车到达丙地时,慢车距丙地还有
10.如图,正比例函数与一次函数的图象交于点.下面四个结论:①;②;③不等式的解集是;④当时,.其中正确的是
A.①② B.②③ C.①④ D.①③
二、填空题
11.直线沿轴向上平移3个单位得到的直线表达式是 .
12.已知一次函数,若的值随的增大而增大,则的取值范围是 .
13.将直线沿轴方向向上平移3个单位,所得新图象的函数表达式是 .
14.已知一次函数的图象经过点与,那么关于的不等式的解集是 .
15.已知点和点在函数的图象上,那 (填“”、“ ”或“” .
16.已知一次函数,当时,总有,则的取值范围为 .
17.一次函数的图象上有一点,将点向右平移1个单位,再向下平移2个单位得到点,若点也在该函数的图象上,则 .
18.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米时,两车之间的距离(千米)与货车行驶时间(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米时;
②图中点的坐标为,;
③甲、乙两地之间的距离为120千米;
④快递车从乙地返回时的速度为90千米时.
以上4个结论正确的是 .
三、解答题
19.已知与的关系式是,且时,.
(1)求与之间的函数关系式;
(2)若点在这个函数的图象上,求点的坐标.
20.疫情过后地摊经济迅速兴起,小李以每千克2元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额(元与销售量(千克)之间的关系如图所示.
(1)求降价后销售额(元与销售量(千克)之间的函数表达式;
(2)当销售量为多少千克时,小李销售此种水果的利润为150元?
21.如图,在平面直角坐标系中,是坐标原点.已知点,,,直线.
(1)求直线的解析式;
(2)若直线经过点.
①当时,求的值;
②若直线与线段有交点,直接写出的取值范围.
22.甲、乙两人从学校出发,甲先出发,乙后出发,都匀速骑车前往图书馆,乙在骑行途中休息片刻后,以原速度继续骑行.已知乙的速度是甲的1.6倍,甲、乙两人离学校的距离(米与乙行驶的时间(分钟)之间的关系如图,请根据图象回答问题.
(1)乙骑行的速度是 米分钟;甲骑行的速度是 米分钟;
(2)甲比乙先出发 分钟;
(3)求线段所表示的与之间的函数解析式.
23.已知一次函数的图象经过点,两点.
(1)求一次函数的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求这个一次函数与坐标轴围成的三角形面积.
24.今年初,很多商场由于受新型冠状病毒肺炎疫情的影响,产品销售情况不如人意.有甲、乙两家商场利用网络平台进行销售.其中甲商场所有商品按9折出售,乙商场对一次购物中超过200元后的金额打折为1到9之间的整数).设顾客所购商品原来金额为元,在甲、乙两家商场实际支付金额分别为元和元.
(1)顾客在乙商场购物时,与之间函数图象如图所示(图中线段和射线,求当时,与之间函数解析式;
(2)当时,甲、乙两个商场中,去哪商场购物更省钱?
25.随着我国防疫形势进一步好转,各景区陆续开始对游客开放,某景区对团体门票采用灵活的售票方法,设团体人数为人,非节假日购票款为(元,节假日购票款为(元,、与之间的函数图象如图所示.
(1)非节假日门票定价是 元人;
(2)当时,与之间的函数关系式 ;
(3)某导游于10月1日(节假日)带团,10月12日(非节假日)带团到该景区,共付门票款1900元,、两个团队游客合计50人(且两团游客人数均超过15人).求:、两个团队游客各有多少人?
26.对于平面直角坐标系内的点和点,若点能绕着点旋转之后,落在轴上,则称是的转换点.
(1)已知点.
①如图,在,,中,是的转换点的是 ;
②是点的转换点,则的取值范围是 ;
(2)已知直线上所有点都是的转换点,直接写出的取值范围.
答案
一、选择题.
1.【分析】根据一次函数定义:形如,、是常数)的函数,叫做一次函数进行分析即可.
【解析】、是一次函数,故此选项符合题意;
、,当时是一次函数,故此选项不符合题意;
、不是一次函数,右边不是整式,故此选项不符合题意;
、不是一次函数,的指数为2,故此选项不符合题意;
故选:.
2.【分析】由直线的解析式,利用一次函数图象与系数的关系,可得出直线的图象经过的象限,此题得解.
【解析】,,
直线的图象经过第一、三、四象限.
故选:.
3.【分析】根据一次函数的性质即可求解.
【解析】一次函数的图象不经过第四象限,
,
解得,
故选:.
4.【分析】代入求出与之对应的值,此题得解.
【解析】当时,,
直线的截距为.
故选:.
5.【分析】运用分类讨论的数学思想,分为腰或底两种情况来分类解析,逐一判断,即可解决问题.
【解析】如图,对于直线,
当时,;
当时,,
直线与两个坐标轴的交点分别为,;
若以点为圆心,以的长为半径画弧,
则与轴有两个交点,与轴有一个交点(点除外);
若以点为圆心,以的长为半径画弧,
则与轴有一个交点(点除外),与轴有两个交点;
以为腰的等腰有6个;
若以为底,作的垂直平分线,与坐标轴交于原点,
综上所述,满足条件的点最多有7个,
故选:.
6.【分析】由直线经过一、二、四象限可分析,,由此判定不经过第二象限.
【解析】直线经过第一、二、四象限,
,,
直线一定不经过第二象限.
故选:.
7.【分析】根据图象的性质,当即图象在轴右方,.
【解析】根据图象和数据可知,当即图象在轴右方,.
故选:.
8.【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距地的距离;
④求出乙到达终点的路程就是,两地距离.
【解析】①由题意,得
甲的速度为:千米时;
设乙的速度为千米时,由题意,得
,
解得:.
即乙的速度为7千米时,
故①正确;
②乙到终点时甲、乙相距的距离为:
千米,故②正确;
③当乙追上甲时,两人距地距离为:
千米.故③正确;
④,两地距离为:
千米,故④错误.
综上所述:错误的只有④.
故选:.
9.【分析】.因为两车同时出发,同向而行,所以点就是甲、乙两地之间的距离为;
.由点为两车的路程差,相遇时间为2小时,可知:快车速度慢车速度,再由点可知慢车从乙地到达丙地;由此求出慢车速度,进一步求出快车速度,进而得出快车从甲地驶到丙地所用时间;
.通过求出列出的速度判断即可;
.根据“路程速度时间”即可.
【解析】点,
甲、乙两地之间的距离为,故说法正确,不符合题意;
点纵坐标为,即快慢两车的距离为0,
点表示时,快车追上慢车,
慢车速度:,快车速度:,
快车速度是慢车速度的1.5倍;故说法正确,不符合题意;
快车速度是,
快车从甲地驶到丙地共用了,故说法错误,符合题意;
两车同时出发,同向而行,
慢车距丙地的距离为:,故说法正确,不符合题意;
故选:.
10.【分析】根据正比例函数和一次函数的性质判断即可.
【解析】因为正比例函数经过二、四象限,所以,①正确;
一次函数经过一、二、三象限,所以,②错误;
由图象可得:不等式的解集是,③正确;
当时,,④错误;
故选:.
二、填空题
11.【分析】根据“上加下减”的原则进行解答即可.
【解析】直线沿轴向上平移3个单位得到的直线表达式是:,即.
故答案是:.
12.【分析】根据一次函数图象与系数的关系可判断.
【解析】一次函数一次函数中,的值随的增大而增大,
,
故答案是:.
13.【分析】根据“上加下减”的原则进行解答即可.
【解析】由“上加下减”的原则可知,将直线沿轴方向向上平移3个单位所得函数的解析式为,即.
故答案为:.
14.【分析】首先利用图象可找到图象在轴上方时,进而得到关于的不等式的解集是.
【解析】由题意可得:一次函数中,时,图象在轴上方,,
则关于的不等式的解集是,
故答案是:.
15.【分析】分别将和代入,表示出、,作差即可比较其大小.
【解析】点和点在函数的图象上,
,,
,
,
故答案为:.
16.【分析】分及两种情况考虑,利用一次函数的性质及一次函数图象上点的坐标特征,即可得出关于的一元一次不等式,解之即可得出结论.
【解析】当时,随的增大而增大,
,解得:,
;
当时,随的增大而减小,
,解得:,
.
故答案为:或.
17.【分析】根据平移的特性写出点的坐标,由点、均在一次函数的图象上,代入解得即可.
【解析】点的坐标为,则点的坐标为,
依题意得:,
解得:,
故答案为:0.
18.【分析】根据题意和函数图象中的数据,可以计算出各个小题中的结论是否正确,从而可以解答本题.
【解析】设快递车从甲地到乙地的速度为千米时,
,
解得,
即快递车从甲地到乙地的速度为100千米时,故①正确;
由已知可得,点的横坐标为:,纵坐标为:,
即点的坐标为,,故②正确;
甲乙两地之间的距离为(千米),故③错误;
设快递车从乙地返回时的速度为千米小时,
,
解得,故④正确;
故答案为:①②④.
三、解答题
19.(1)与的函数关系是,
把,代入得:,
解得:.
则与函数关系式为;
(2)把点代入,
得:,
解得,
所以点的坐标是.
20.(1)设降价后销售额(元与销售量(千克)之间的函数表达式是,
段过点,,
,
解得,,
即降价后销售额(元与销售量(千克)之间的函数表达式是;
(2)设当销售量为千克时,小李销售此种水果的利润为150元,
,
解得,,
答:当销售量为180千克时,小李销售此种水果的利润为150元.
21.(1)设直线的解析式为,把点,代入得:
,解得:,
直线的解析式为;
(2)①把,代入得:
,解得:,
的值为;
②把代入得,即,
把点代入得:,解得:,
把点代入得:,解得:,
的取值范围为:1≤b≤3.
22.(1)由图象可得,
乙骑行的速度为:(米分钟),
甲骑行的速度为:(米分钟),
故答案为:320,200;
(2)甲从学校到图书馆的时间为:(分钟),
甲比乙先出发(分钟),
故答案为:2;
(3)点的纵坐标为:,
故点的坐标为,点的坐标为,
设线段所表示的与之间的函数解析式是,
,
解得,
即线段所表示的与之间的函数解析式是y=200x+400(0≤x≤300).
23.(1)一次函数的图象经过两点、,
,
函数解析式为:;
(2)函数图象如图
;
(3)一次函数与轴的交点为,
的面积.
24.(1)设当时,与之间函数解析式为,
由图象得,,
解得:,
当时,与之间函数解析式为;
(2)当时,
甲商场实际支付金额为(元,
乙商场实际支付金额为(元,
所以当时,去乙商场购物更省钱.
25.(1)由图象可得与之间为正比例函数,时,,
(元,
故答案为:30;
(2)当时,设,
函数图象经过点和,
,
,
,
故答案为:;
(3)设团有人,表示出团的人数为人,
当时,,
解得,
(人,
答:团有25人,团有25人.
26.(1)①,,.
,,.
的转换点的是,.
②如图,点轨迹为直线.
.
当时解得.
或.
(2)如图,作直线于点.直线交轴轴于点,.
,,.
.
即.
由题意得到直线距离到轴距离,即 ≥,
①t≥0时,0≤t≤3.
②时,-≤t<0.
③t≤-2时无解.
故答案为:-≤t≤3.
