八年级数学下册试题 第二十二章《四边形》单元复习题 -沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第二十二章《四边形》单元复习题 -沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 08:35:11 | ||
图片预览


文档简介
第二十二章《四边形》单元复习题
一、单选题
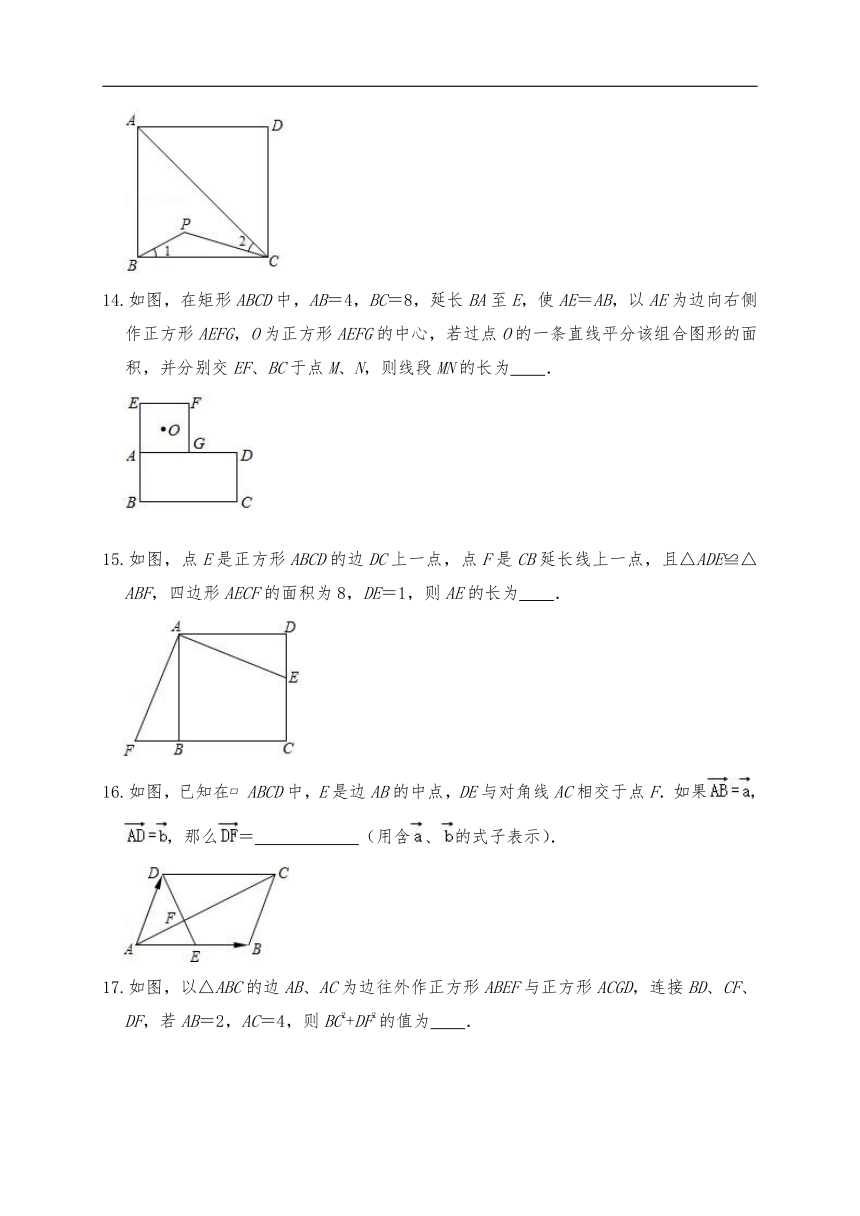
1.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
2.如图,在菱形ABCD中,对角线AC=6,∠BAD=120°,则菱形ABCD的周长为( )
A.24 B.30 C.36 D.18
3.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
4.如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )
A.① B.② C.③ D.④
5.已知,是两个非零向量,是一个单位向量,下列等式中正确的是( )
A.= B.= C.||= D.||=
6.如图,在平行四边形ABCD中,AD=2AB,作CE⊥AB于点E,点F是AD的中点,连接CF,EF.关于下列四个结论:①∠BCF=∠DCF;②∠FEC=∠FCE;③∠AEF=∠CFD;④S△CEF=S△BCE,则所有正确结论的序号是( )
A.①②③④ B.①②③ C.②③④ D.③④
二、填空题
7.在 ABCD中,若∠A+∠C=342°,则∠B= 度.
8.如图, ABCD的一个外角∠CBE是70°,则∠D的大小是 .
9.在 ABCD中,已知周长为44cm,AB比BC短2cm,则CD=
10.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为 .
11.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
12.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
13.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
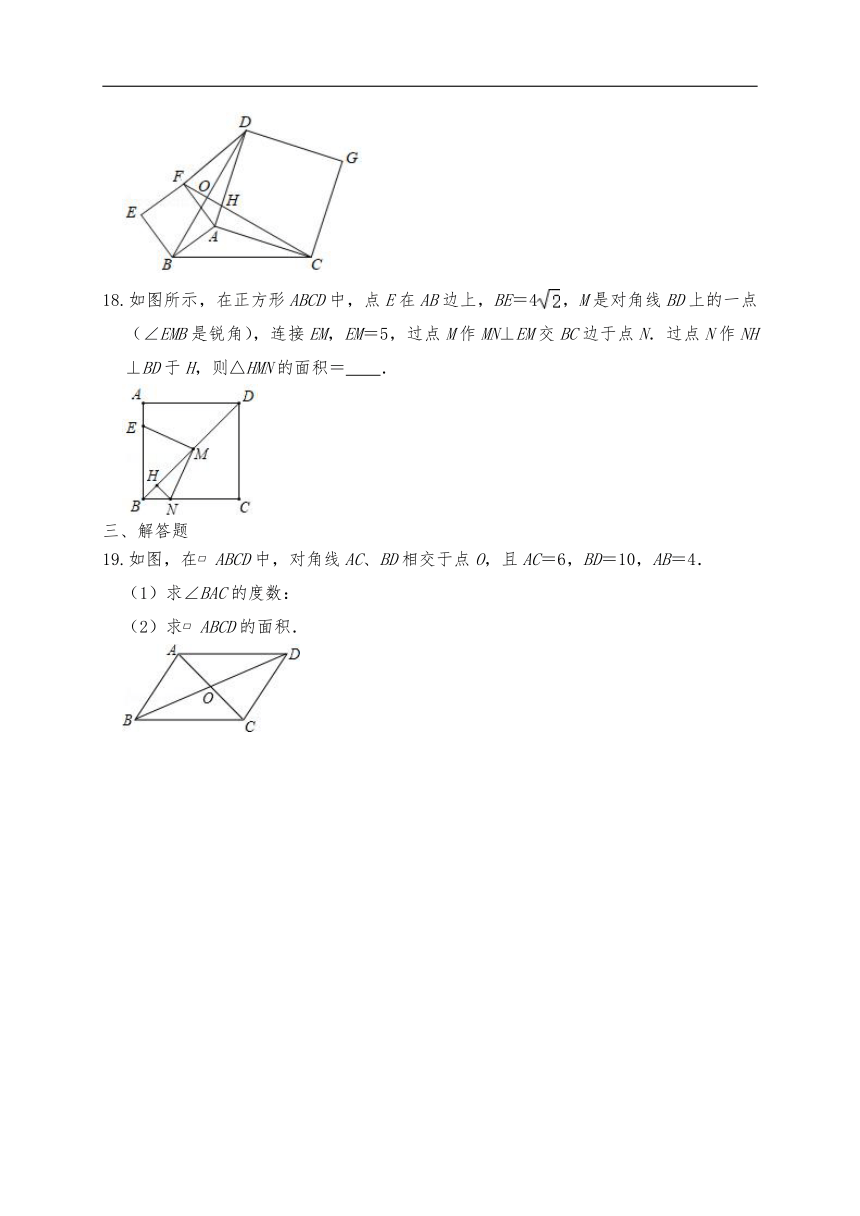
14.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
15.如图,点E是正方形ABCD的边DC上一点,点F是CB延长线上一点,且△ADE≌△ABF,四边形AECF的面积为8,DE=1,则AE的长为 .
16.如图,已知在 ABCD中,E是边AB的中点,DE与对角线AC相交于点F.如果,,那么= (用含、的式子表示).
17.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为 .
18.如图所示,在正方形ABCD中,点E在AB边上,BE=4,M是对角线BD上的一点(∠EMB是锐角),连接EM,EM=5,过点M作MN⊥EM交BC边于点N.过点N作NH⊥BD于H,则△HMN的面积= .
三、解答题
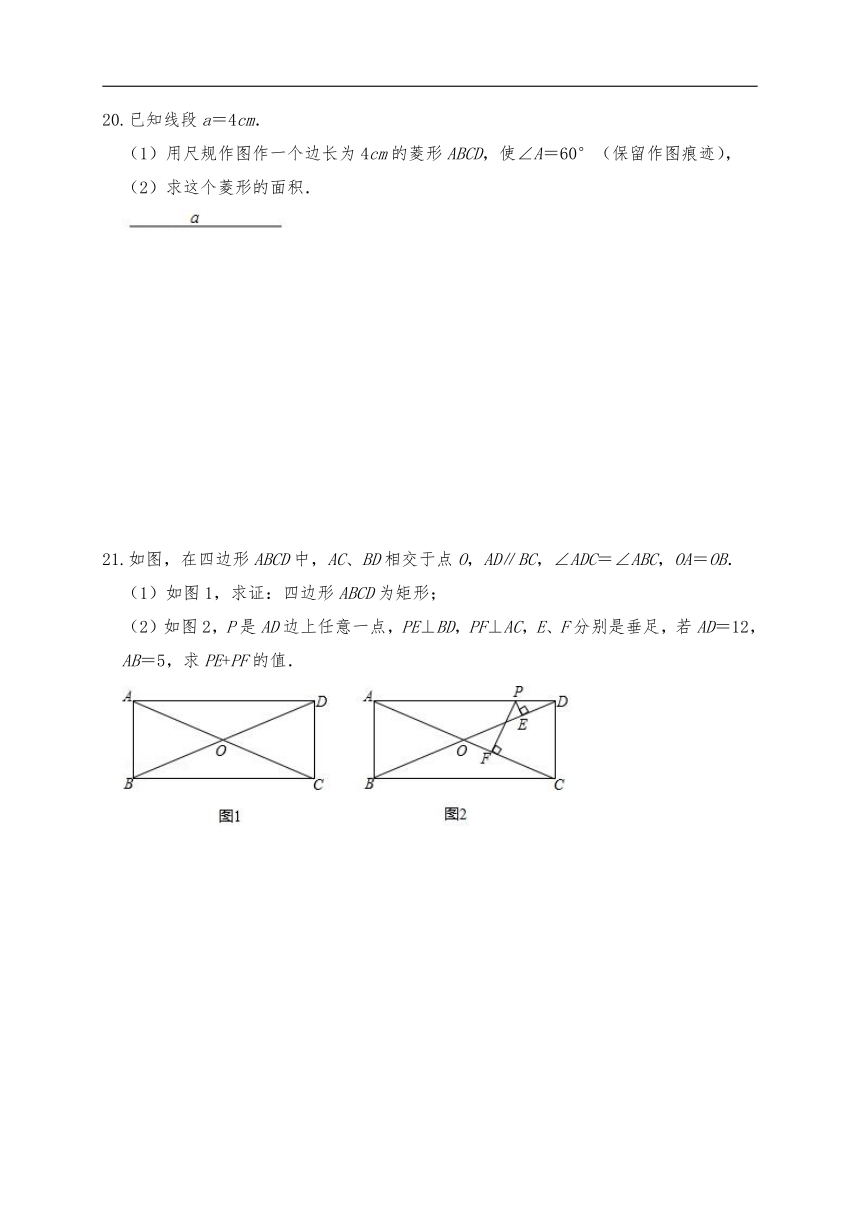
19.如图,在 ABCD中,对角线AC、BD相交于点O,且AC=6,BD=10,AB=4.
(1)求∠BAC的度数:
(2)求 ABCD的面积.
20.已知线段a=4cm.
(1)用尺规作图作一个边长为4cm的菱形ABCD,使∠A=60°(保留作图痕迹),
(2)求这个菱形的面积.
21.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
22.已知:在矩形ABCD中,点E在BC边上,连接DE,且DE=BC,过点A作AF⊥DE于点F.
(1)如图1,求证:AB=AF;
(2)如图2,连接AE,当BE=DF时,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于AB的线段.
23.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线AB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
24.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE=2AE.设=,=.
(1)填空:向量= ﹣ ;
(2)如果点F是线段OC的中点,那么向量= ,并在图中画出向量在向量和方向上的分向量.
(注:本题结果用向量,的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量).
25.问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=,PB=,PC=1.求∠BPC的度数和正方形ABCD的边长.
答案
一、单选题
1.A
【解答】解:A.因为对角线互相垂直,正方形具有而矩形不具有,所以A选项符合题意;
B.因为对角线相等,正方形具有而矩形也具有,所以B选项不符合题意;
C.因为对角互补,正方形具有而矩形也具有,所以C选项不符合题意;
D.因为四个角相等,正方形具有而矩形也具有,所以D选项不符合题意.
故选:A.
2.A
【解答】解:在菱形ABCD中,∠BAD=120°,
∴∠B=180°﹣120°=60°,
又∵AB=BC,
∴△ABC是等边三角形,
∴AB=AC=6,
∴菱形ABCD的周长=6×4=24.
故选:A.
3.C
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵ ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在 ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC﹣BE=6﹣2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
4.C
【解答】解:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B=∠DCF,
①∵添加BE=CF,
∴△BCE≌△CDF(SAS),
②∵添加CE⊥AB,DF⊥BC,
∴∠CEB=∠F=90°,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④∵添加∠BCE=∠CDF,
∴△BCE≌△CDF(ASA),
故选:C.
5.D
【解答】解:A、得出的是a的方向不是单位向量,故错误;
B、左边得出的是a的方向,右边得出的是b的方向,两者方向不一定相同,故错误;
C、由于单位向量只限制长度,不确定方向,故错误;
D、符合向量的长度及方向,故正确;
故选:D.
6.B
【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,AB=CD,
∴∠DFC=∠BCF,
∵点F是AD的中点,
∴AD=2DF,
∵AD=2AB,
∴AD=2CD,
∴DF=CD,
∴∠DFC=∠DCF,
∴∠BCF=∠DCF,故①正确;
取EC的中点G,连接FG,则FG为梯形AECD的中位线,
∴FG∥AB,
∵CE⊥AB,
∴FG⊥CE,
∴EF=CF,
∴∠FEC=∠FCE,故②正确;
∵CE⊥AB,AB∥CD,
∴CE⊥CD,
∴∠AEC=∠DCE=90°,
即∠AEF+∠FEC=∠DCF+∠FCE=90°,
∴∠AEF=∠DCF,
∵∠DCF=∠CFD,
∴∠AEF=∠CFD,故③正确;
根据现有条件无法证明S△CEF=S△BCE,故错误④.
故选:B.
二、填空题
7.9
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠A+∠B=180°,
∵∠A+∠C=342°,
∴∠A=171°,
∴∠B=180°﹣171°=9°,
故答案为:9.
8.110°
【解答】解:∵∠CBE=70°,
∴∠CBA=110°,
在平行四边形中,
∴∠D=∠CBA=110°,
故答案为:110°.
9.10cm.
【解答】解:由四边形ABCD是平行四边形,可知:
2(AB+BC)=44cm,
且BC﹣AB=2cm,
∴,
解得BC=12,AB=10,
∴CD=AB=10cm.
故答案为:10cm.
10.4
【解答】解:∵OA=1,OB=2,
∴AC=2,BD=4,
∴菱形ABCD的面积为×2×4=4.
故答案为:4.
11.5
【解答】解:如图,∵在Rt△ABC中,∠ABC=90°,F为CA的中点,BF=5,
∴AC=2BF=10.
又∵D、E分别为AB、BC的中点,
∴DE是Rt△ABC的中位线,
∴DE=AC=5.
故答案是:5.
12.
【解答】解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
13.135
【解答】解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
14.
【解答】解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
15.3
【解答】解:∵△ADE≌△ABF,
∴正方形ABCD的面积等于四边形AECF的面积,
∵四边形AECF的面积为8,
∴正方形ABCD的面积为8.
∴AD2=8,
在Rt△ADE中,AE===3,
故答案为:3.
16.解:∵DF:EF=DC:AE=2:1,
∴DF:DE=,
∵=﹣=﹣,
∴=(﹣)=﹣.
故答案为:﹣.
17.40
【解答】解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
18.6
【解答】解:如图所示,过M作MP⊥AB于P,MQ⊥BC于Q,则∠EPM=∠NQM=90°,
∴∠PMQ=90°=∠EMN,
∴∠EMP=∠NMQ,
又∵MB平分∠ABC,
∴MP=MQ,
∴△EPM≌△NQM(ASA),
∴EM=NM,
如图所示,过E作EF⊥BD于F,则∠EFM=90°,
∵NH⊥BD,
∴∠MHN=90°,
又∵∠EMN=90°,
∴∠EMF+∠HMN=∠MNH+∠HMN=90°,
∴∠EMF=∠MNH,
∴△EMF≌△MNH(AAS),
∴FM=HN,
∵∠EBM=45°,
∴∠BEF=45°=∠EBF,
∴△BEF是等腰直角三角形,
又∵BE=4,
∴EF=BF=4,
又∵EM=5,
∴Rt△EFM中,FM=3,
∴HN=3=BH,
∴HF=BF﹣BH=4﹣3=1,
∴HM=1+3=4,
∴△HMN的面积=HM×HN=×4×3=6,
故答案为:6.
三、解答题
19.解:(1)∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=6,BD=10,
∴AO=3,BO=5,
∵AB=4,
∴AB2+AO2=OB2,
∴∠BAC=90°;
(2) ABCD的面积=AB×AC=4×6=24.
20.解:(1)如图所示:四边形ABCD即为所求;
(2)过点D作DH⊥AB于点H,
∵∠A=60°,AD=4cm,
∴∠DAH=30°,则AH=AD=2cm,
故DH==2(cm),
则这个菱形的面积为:AB DH=4×2=8(cm2).
21.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
22.证明:(1)∵四边形ABCD是矩形,AF⊥DE,
∴AD∥BC,AD=BC,AB=CD,∠C=∠AFD=90°,
∴∠ADE=∠DEC,
∵DE=BC,
∴AD=DE,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AF=CD,
∴AF=AB;
(2)AD,BC,DE的长度等于AB,
理由如下:∵△ADF≌△DEC,
∴CE=DF,
∴BE=EF,
∵BE=DF,
∴BE=EC=DF=EF,
∴DE=2EC,
∵DE2=EC2+CD2,
∴DE=AB,
∴AD=BC=DE=AB.
23.解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,);
(2)设直线OB的解析式是y=k1x,
把B点坐标代入,得k1=,
则直线OB的解析式是y=x.
设反比例函数解析式是y=,
把E点坐标代入,得k2=3,
则反比例函数的解析式是y=;
(2)由题意得Fy=3,代入,
得Fx=1,即F(1,3).
则四边形OEBF的面积=矩形OABC的面积﹣△OAE的面积﹣△OCF的面积=2×3﹣1×3﹣2×=3.
24.解:(1)∵=,BE=2AE,
∴=,
∵=+=﹣+.
故答案为﹣+.
(2)∵=+=+,AF=AC,
∴=+,
∵=+=﹣++=+.
向量在向量和方向上的分向量分别为:,(如图所示)
故答案为=+.
25.解:(1)根据旋转可知:
∠AP′B=150°,∠BPC=∠AP′B=150°,
等边三角形ABC的边长为.
故答案为150°、150°、.
(2)解:将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP′=PB=.
连接PP′,如图.在Rt△BP′P中,
∵PB=BP′=,∠PBP′=90°,
∴PP′=2,∠BP′P=45°.
在△AP′P中,AP′=1,PP′=2,PA=,
∵12+22=()2,
即AP′2+PP′2=PA2,
∴△AP′P是直角三角形,
即∠AP′P=90°.
∴∠AP′B=135°,
∴∠BPC=∠AP′B=135°.
过点B作BE⊥AP′,交AP′的延长线于点E,则△BEP′是等腰直角三角形,
∴∠EP′B=45°.
又∵BP′=,
∴EP′=BE=1,∴AE=2.
在Rt△ABE中,
∵BE=1,AE=2,
∴由勾股定理,得AB=.
综上可得,∠BPC=135°,正方形ABCD的边长为.
答:∠BPC的度数为135°,正方形ABCD的边长为.
一、单选题
1.正方形具有而矩形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角互补 D.四个角相等
2.如图,在菱形ABCD中,对角线AC=6,∠BAD=120°,则菱形ABCD的周长为( )
A.24 B.30 C.36 D.18
3.如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是( )
A.60 B.30 C.20 D.16
4.如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是( )
A.① B.② C.③ D.④
5.已知,是两个非零向量,是一个单位向量,下列等式中正确的是( )
A.= B.= C.||= D.||=
6.如图,在平行四边形ABCD中,AD=2AB,作CE⊥AB于点E,点F是AD的中点,连接CF,EF.关于下列四个结论:①∠BCF=∠DCF;②∠FEC=∠FCE;③∠AEF=∠CFD;④S△CEF=S△BCE,则所有正确结论的序号是( )
A.①②③④ B.①②③ C.②③④ D.③④
二、填空题
7.在 ABCD中,若∠A+∠C=342°,则∠B= 度.
8.如图, ABCD的一个外角∠CBE是70°,则∠D的大小是 .
9.在 ABCD中,已知周长为44cm,AB比BC短2cm,则CD=
10.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为 .
11.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
12.已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB=6,AC=2,则DE的长是 .
13.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
14.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
15.如图,点E是正方形ABCD的边DC上一点,点F是CB延长线上一点,且△ADE≌△ABF,四边形AECF的面积为8,DE=1,则AE的长为 .
16.如图,已知在 ABCD中,E是边AB的中点,DE与对角线AC相交于点F.如果,,那么= (用含、的式子表示).
17.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为 .
18.如图所示,在正方形ABCD中,点E在AB边上,BE=4,M是对角线BD上的一点(∠EMB是锐角),连接EM,EM=5,过点M作MN⊥EM交BC边于点N.过点N作NH⊥BD于H,则△HMN的面积= .
三、解答题
19.如图,在 ABCD中,对角线AC、BD相交于点O,且AC=6,BD=10,AB=4.
(1)求∠BAC的度数:
(2)求 ABCD的面积.
20.已知线段a=4cm.
(1)用尺规作图作一个边长为4cm的菱形ABCD,使∠A=60°(保留作图痕迹),
(2)求这个菱形的面积.
21.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
22.已知:在矩形ABCD中,点E在BC边上,连接DE,且DE=BC,过点A作AF⊥DE于点F.
(1)如图1,求证:AB=AF;
(2)如图2,连接AE,当BE=DF时,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于AB的线段.
23.如图,将一个长方形放置在平面直角坐标系中,OA=2,OC=3,E是AB中点,反比例函数图象过点E且和BC相交点F.
(1)直接写出点B和点E的坐标;
(2)求直线AB与反比例函数的解析式;
(3)连接OE、OF,求四边形OEBF的面积.
24.如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE=2AE.设=,=.
(1)填空:向量= ﹣ ;
(2)如果点F是线段OC的中点,那么向量= ,并在图中画出向量在向量和方向上的分向量.
(注:本题结果用向量,的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量).
25.问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=,PB=,PC=1.求∠BPC的度数和正方形ABCD的边长.
答案
一、单选题
1.A
【解答】解:A.因为对角线互相垂直,正方形具有而矩形不具有,所以A选项符合题意;
B.因为对角线相等,正方形具有而矩形也具有,所以B选项不符合题意;
C.因为对角互补,正方形具有而矩形也具有,所以C选项不符合题意;
D.因为四个角相等,正方形具有而矩形也具有,所以D选项不符合题意.
故选:A.
2.A
【解答】解:在菱形ABCD中,∠BAD=120°,
∴∠B=180°﹣120°=60°,
又∵AB=BC,
∴△ABC是等边三角形,
∴AB=AC=6,
∴菱形ABCD的周长=6×4=24.
故选:A.
3.C
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵ ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
在 ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC﹣BE=6﹣2=4,
∴CD=AB=4,
∴ ABCD的周长=6+6+4+4=20.
故选:C.
4.C
【解答】解:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,
∴∠B=∠DCF,
①∵添加BE=CF,
∴△BCE≌△CDF(SAS),
②∵添加CE⊥AB,DF⊥BC,
∴∠CEB=∠F=90°,
∴△BCE≌△CDF(AAS),
③∵添加CE=DF,
不能确定△BCE≌△CDF;
④∵添加∠BCE=∠CDF,
∴△BCE≌△CDF(ASA),
故选:C.
5.D
【解答】解:A、得出的是a的方向不是单位向量,故错误;
B、左边得出的是a的方向,右边得出的是b的方向,两者方向不一定相同,故错误;
C、由于单位向量只限制长度,不确定方向,故错误;
D、符合向量的长度及方向,故正确;
故选:D.
6.B
【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,AB=CD,
∴∠DFC=∠BCF,
∵点F是AD的中点,
∴AD=2DF,
∵AD=2AB,
∴AD=2CD,
∴DF=CD,
∴∠DFC=∠DCF,
∴∠BCF=∠DCF,故①正确;
取EC的中点G,连接FG,则FG为梯形AECD的中位线,
∴FG∥AB,
∵CE⊥AB,
∴FG⊥CE,
∴EF=CF,
∴∠FEC=∠FCE,故②正确;
∵CE⊥AB,AB∥CD,
∴CE⊥CD,
∴∠AEC=∠DCE=90°,
即∠AEF+∠FEC=∠DCF+∠FCE=90°,
∴∠AEF=∠DCF,
∵∠DCF=∠CFD,
∴∠AEF=∠CFD,故③正确;
根据现有条件无法证明S△CEF=S△BCE,故错误④.
故选:B.
二、填空题
7.9
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠A+∠B=180°,
∵∠A+∠C=342°,
∴∠A=171°,
∴∠B=180°﹣171°=9°,
故答案为:9.
8.110°
【解答】解:∵∠CBE=70°,
∴∠CBA=110°,
在平行四边形中,
∴∠D=∠CBA=110°,
故答案为:110°.
9.10cm.
【解答】解:由四边形ABCD是平行四边形,可知:
2(AB+BC)=44cm,
且BC﹣AB=2cm,
∴,
解得BC=12,AB=10,
∴CD=AB=10cm.
故答案为:10cm.
10.4
【解答】解:∵OA=1,OB=2,
∴AC=2,BD=4,
∴菱形ABCD的面积为×2×4=4.
故答案为:4.
11.5
【解答】解:如图,∵在Rt△ABC中,∠ABC=90°,F为CA的中点,BF=5,
∴AC=2BF=10.
又∵D、E分别为AB、BC的中点,
∴DE是Rt△ABC的中位线,
∴DE=AC=5.
故答案是:5.
12.
【解答】解:如图,
∵四边形ABCD是矩形,
∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC===2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE=;
当点E'在AB上时,
∵CE'2=BE'2+BC2=E'A2,
∴AE'2=(6﹣AE')2+4,
∴AE'=,
∴DE'===,
综上所述:DE=或,
故答案为:或.
13.135
【解答】解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
14.
【解答】解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
15.3
【解答】解:∵△ADE≌△ABF,
∴正方形ABCD的面积等于四边形AECF的面积,
∵四边形AECF的面积为8,
∴正方形ABCD的面积为8.
∴AD2=8,
在Rt△ADE中,AE===3,
故答案为:3.
16.解:∵DF:EF=DC:AE=2:1,
∴DF:DE=,
∵=﹣=﹣,
∴=(﹣)=﹣.
故答案为:﹣.
17.40
【解答】解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
18.6
【解答】解:如图所示,过M作MP⊥AB于P,MQ⊥BC于Q,则∠EPM=∠NQM=90°,
∴∠PMQ=90°=∠EMN,
∴∠EMP=∠NMQ,
又∵MB平分∠ABC,
∴MP=MQ,
∴△EPM≌△NQM(ASA),
∴EM=NM,
如图所示,过E作EF⊥BD于F,则∠EFM=90°,
∵NH⊥BD,
∴∠MHN=90°,
又∵∠EMN=90°,
∴∠EMF+∠HMN=∠MNH+∠HMN=90°,
∴∠EMF=∠MNH,
∴△EMF≌△MNH(AAS),
∴FM=HN,
∵∠EBM=45°,
∴∠BEF=45°=∠EBF,
∴△BEF是等腰直角三角形,
又∵BE=4,
∴EF=BF=4,
又∵EM=5,
∴Rt△EFM中,FM=3,
∴HN=3=BH,
∴HF=BF﹣BH=4﹣3=1,
∴HM=1+3=4,
∴△HMN的面积=HM×HN=×4×3=6,
故答案为:6.
三、解答题
19.解:(1)∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=6,BD=10,
∴AO=3,BO=5,
∵AB=4,
∴AB2+AO2=OB2,
∴∠BAC=90°;
(2) ABCD的面积=AB×AC=4×6=24.
20.解:(1)如图所示:四边形ABCD即为所求;
(2)过点D作DH⊥AB于点H,
∵∠A=60°,AD=4cm,
∴∠DAH=30°,则AH=AD=2cm,
故DH==2(cm),
则这个菱形的面积为:AB DH=4×2=8(cm2).
21.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
22.证明:(1)∵四边形ABCD是矩形,AF⊥DE,
∴AD∥BC,AD=BC,AB=CD,∠C=∠AFD=90°,
∴∠ADE=∠DEC,
∵DE=BC,
∴AD=DE,
在△ADF和△DEC中,
,
∴△ADF≌△DEC(AAS),
∴AF=CD,
∴AF=AB;
(2)AD,BC,DE的长度等于AB,
理由如下:∵△ADF≌△DEC,
∴CE=DF,
∴BE=EF,
∵BE=DF,
∴BE=EC=DF=EF,
∴DE=2EC,
∵DE2=EC2+CD2,
∴DE=AB,
∴AD=BC=DE=AB.
23.解:(1)∵OA=2,OC=3,E是AB中点,
∴B(2,3),E(2,);
(2)设直线OB的解析式是y=k1x,
把B点坐标代入,得k1=,
则直线OB的解析式是y=x.
设反比例函数解析式是y=,
把E点坐标代入,得k2=3,
则反比例函数的解析式是y=;
(2)由题意得Fy=3,代入,
得Fx=1,即F(1,3).
则四边形OEBF的面积=矩形OABC的面积﹣△OAE的面积﹣△OCF的面积=2×3﹣1×3﹣2×=3.
24.解:(1)∵=,BE=2AE,
∴=,
∵=+=﹣+.
故答案为﹣+.
(2)∵=+=+,AF=AC,
∴=+,
∵=+=﹣++=+.
向量在向量和方向上的分向量分别为:,(如图所示)
故答案为=+.
25.解:(1)根据旋转可知:
∠AP′B=150°,∠BPC=∠AP′B=150°,
等边三角形ABC的边长为.
故答案为150°、150°、.
(2)解:将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.
∴AP′=PC=1,BP′=PB=.
连接PP′,如图.在Rt△BP′P中,
∵PB=BP′=,∠PBP′=90°,
∴PP′=2,∠BP′P=45°.
在△AP′P中,AP′=1,PP′=2,PA=,
∵12+22=()2,
即AP′2+PP′2=PA2,
∴△AP′P是直角三角形,
即∠AP′P=90°.
∴∠AP′B=135°,
∴∠BPC=∠AP′B=135°.
过点B作BE⊥AP′,交AP′的延长线于点E,则△BEP′是等腰直角三角形,
∴∠EP′B=45°.
又∵BP′=,
∴EP′=BE=1,∴AE=2.
在Rt△ABE中,
∵BE=1,AE=2,
∴由勾股定理,得AB=.
综上可得,∠BPC=135°,正方形ABCD的边长为.
答:∠BPC的度数为135°,正方形ABCD的边长为.
