第四单元 正比例与反比例(复习课件)-六年级数学下学期期中核心考点集训(北师大版)(共26张PPT)
文档属性
| 名称 | 第四单元 正比例与反比例(复习课件)-六年级数学下学期期中核心考点集训(北师大版)(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 20:53:06 | ||
图片预览







文档简介
(共26张PPT)
第四单元 正比例与反比例
六年级下册 北师大版
一、知识导图
二、考点梳理
知识点① 变化的量
相关联的两个量,一个量随另一个量的变化而变化。
二、考点梳理
知识点② 正比例
两个相关联的量,一个量随另一个量的变化而变化,且这两个量的比值(也就是商)
一定,我们就说这样的两个量成正比例。
二、考点梳理
知识点③ 正比例的图象
1.正比例的图象是一条直线。
2.判断某一点在不在这条直线上,要看这个点所对应的两个数的比值与原成正比例
的两个量的比值是否相等,相等就在这条直线上,否则不在。
二、考点梳理
知识点④ 反比例
两个相关联的量,一个量随另一个量的变化而变化,且这两个量的乘积一定,我们
就说这样的两个量成反比例。
三、典例精讲
分析
典例01
先用男生人数加上女生人数,求出总
人数,用男生人数除以总人数就是男
生人数是全部人数的几分之几;先用
女生人数减去男生人数去求出男生比
女生少多少人,再除以女生人数就是
男生人数比女生少几分之几;写出女
生人数与全部人数的对应比,然后再
化简即可。
比的意义
考点01
解答
点评
解答此题的关键是要找准单位”1“的
量。
学校合唱队中男生有10人,女生有40人,男生人数是全部人数的
,男生人数比女生少 ,女生人数与全部人数的比是 。
解:10+40=50(人),10÷50=
(40﹣10)÷40=30÷40=
40:50=(40÷10):(50÷10)=4:5
答:男生人数是全部人数的 ,男生人数比女生少 ,女生人数与全
部人数的比是 4:5。
故答案为:4:5。
三、典例精讲
分析
变式①
由“大小两个圆的半径比是2:1”,
设小圆的半径为r,则大圆的半径为2r,
分别代入圆的面积公式S=πr2,表示
出各自的面积,再写出相应的比即可.
比的意义
考点01
解答
点评
本题主要是灵活利用圆的面积公式S
=πr2解决问题.
大小两个圆的半径比是2:1,那么大小两个圆的面积的比是 .
解:小圆的面积=πr2,
大圆的面积=π(2r)2=4πr2,
πr2:4πr2=1:4;
答:大小两个圆的面积的比是4:1.
故答案为:4:1.
三、典例精讲
分析
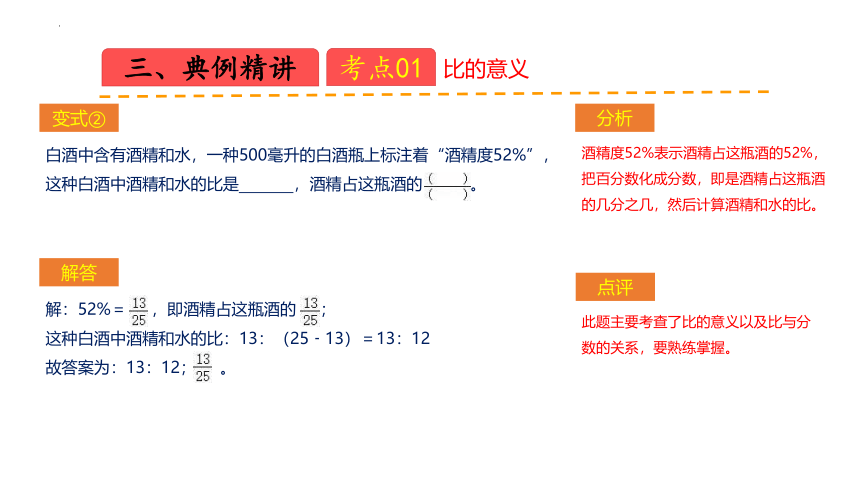
变式②
酒精度52%表示酒精占这瓶酒的52%,
把百分数化成分数,即是酒精占这瓶酒
的几分之几,然后计算酒精和水的比。
比的意义
考点01
解答
点评
此题主要考查了比的意义以及比与分
数的关系,要熟练掌握。
白酒中含有酒精和水,一种500毫升的白酒瓶上标注着“酒精度52%”,
这种白酒中酒精和水的比是 ,酒精占这瓶酒的 。
解:52%= ,即酒精占这瓶酒的 ;
这种白酒中酒精和水的比:13:(25﹣13)=13:12
故答案为:13:12; 。
三、典例精讲
分析
变式③
要求男生人数是女生的几倍,也就是
求25是20的几倍,用除法计算;根
据男生25人,女生20人,可知总人
数为(25+20)人,进而写出各比并
化简比即可;用男生人数减女生人数,
再除以男生人数即可。
比的意义
考点01
解答
点评
解决此题要注意比的前后项分别是哪
一个量,要对应好具体的数量,写出
比再根据比的性质把比化成最简比;
也考查了求一个数是另一个数的几倍
(或几分之几)的解答方法。
一班有男生25人,女生20人。男生人数是女生的 倍,女生人数与
男生人数的最简单的整数比是( : ),女生人数占总人数
的 ,女生人数比男生少 %。
解:25÷20=
20:25=(20÷5):(25÷5)=4:5,20+25=45(人)
20÷45= = ,(25﹣20)÷25=5÷25=20%
答:男生人数是女生的 倍,女生人数与男生人数的最简单的整数比是
4:5,女生人数占总人数的 ,女生人数比男生少20%。
故答案为: ;4;5; ;20。
三、典例精讲
分析
典例02
(1)先求出甲车行驶的时间,再根
据速度=路程÷时间,列式解答。
(2)根据乙的行车轨迹,可以知道
路程和时间成正比例关系,因为路程
是随着时间的变化而变化。
正比例和反比例的意义
考点02
甲乙两车从A地开往B地,在同一条公路上行驶,情况如图所示。
(1)甲车先慢后快,它的平均速度是每小时多少千米?
(2)根据乙的行车轨迹,可以知道哪两种量存在怎样的比例关系?为什么?
三、典例精讲
点评
解答
此题考查了行程问题的知识,解题的
关键是知道速度=路程÷时间,要求
学生掌握。
正比例和反比例的意义
考点02
解:(1)9:30﹣7:00=2:30
2时30分=2.5小时
180÷2.5=72(千米/时)
答:它的平均速度是每小时72千米。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路
程是随着时间的变化而变化。
三、典例精讲
分析
变式①
(1)看图即可找出800千米相对应
的时间;
(2)根据正比例的意义和反比例的
意义进行解答即可:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;
(3)因为这列动车行驶的时间和路
程成正比例,可设4.5小时行驶x千米,
列比例式为x:4.5=200:1,解答
即可.
正比例和反比例的意义
考点02
一列动车在高速铁路上行驶的时间和路程如图.看图填写:
(1)这列动车行800千米需要 小时.
(2)这列动车行驶的时间和路程成 比例.
(3)照这样计算,4.5小时行驶 千米.
三、典例精讲
点评
解答
解答此题的关键是:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;同时考查了分析统计图以及据
此解决问题的能力.
正比例和反比例的意义
考点02
解:(1)这列动车行800千米需要4小时.
(2)400÷2=200,800÷4=200,…
因为;行驶的路程与时间的比值一定,
所以:这列动车行驶的时间和路程成正比例.
(3)设4.5小时行驶x千米,
x:4.5=200:1
2x=4.5×400
x=900
答:4.5小时行驶900千米.
故答案为:4,正,900.
三、典例精讲
分析
变式②
如果a和b成正比例,比值一定,利
用5:0.4求出比值,再利用8除以比
值即可;如果a和b成反比例,那么
乘积一定,利用5×0.4求出积再除以
8即可。
正比例和反比例的意义
考点02
如图中,如果a和b成正比例,空格处应填 ;如果a和b成反比
例,空格处应填 。
a 5 8
b 0.4
点评
解答
此题属于辨识两种相关联的量成什么
比例,就看这两种量是对应的比值一
定,还是对应的乘积一定。
解:8÷(5÷0.4)=8÷12.5=0.64
5×0.4÷8=2÷8=0.25
因此如果a和b成正比例,空格处应填0.64;如果a和b成反比例,空格处
应填0.25。
故答案为:0.64,0.25。
三、典例精讲
分析
变式③
(1)张叔叔骑自行车的路程与时间
成正比例。因为路程÷时间=速度,
速度一定。
正比例和反比例的意义
考点02
张叔叔骑自行车的时间与路程如下表所示。
(1)张叔叔骑自行车的路程与时间成正比例吗?为什么?
(2)先根据上表描点,再顺次连接。
(3)点(6,1.2)在这条直线上吗?这一点表示什么含义?
时间/分 0 1 2 3 4 5
路程/千米 0 0.2 0.4 0.6 0.8 1
三、典例精讲
点评
解答
此题考查了正比例的应用知识,要求
学生掌握。
列竖式计算除法
考点02
解:(1)0.2÷1=0.2(千米/分)
0.4÷2=0.2(千米/分)
0.6÷3=0.2(千米/分)
0.8÷4=0.2(千米/分)
1÷5=0.2(千米/分)
速度一定,所以张叔叔骑自行车的
路程与时间成正比例。
(2)
(3)点(6,1.2)在这条直线上,这一点表示张叔叔骑自行车6分钟,
走了1.2千米的路程。
三、典例精讲
分析
典例03
(1)根据图示可知30秒出水12升,出水
22升需要55秒;
(2)因为出水量除以时间一定,即相对
应的两个数的比值(商)一定,所以成正
比例;
(3)因为出水量和打开时间成正比例,
但每秒出水量比甲水龙头多,所以在甲的
图像上面即可。
右图是甲水龙头打开后出水量情况统计。
(1)根据图像填表。
(2)甲水龙头打开的时间和出水量成 比例。
(3)还有一个乙水龙头,它的出水量和打开时间成正比例,但每秒出水量比甲水龙头多,请在上图中用图像表示出乙水龙头的出水情况。
辨识成正比例的量与成反比例的量
考点03
时间/秒 30
出水量/升 22
三、典例精讲
点评
解答
此题属于根据正、反比例的意义,辨识两
种相关联的量是否成正、反比例,关键是
看这两种相关量中相对应的两个数是商一
定还是积一定,如果商一定,就成正比例;
如果积一定,就成反比例。
解:(1)如下表所示:
(2)因为12÷30=22÷55=0.4(升/秒),即相对应的两个数的比值
(商)一定,所以成正比例。
(3)如下图所示:
故答案为:55;12;正。
辨识成正比例的量与成反比例的量
考点03
时间/秒 30 55
出水量/升 12 22
三、典例精讲
分析
变式①
(1)判断两个相关联的量之间成什么
比例,就看这两个量是对应的比值一定,
还是对应的乘积一定,如果是比值一定,
就成正比例,如果是乘积一定,则成反
比例;
(2)因为平均每天产量和所需时间成
反比例,总台数不变,用总台数除以需
要的天数即可解答。
豆浆是中国人民喜爱的一种饮品,又是一种老少皆宜的营养食品,在欧
美享有“植物奶”的美誉、某工厂要生产一批豆浆机,平均每天产量和
所需时间如表。
(1)平均每天产量与所需时间成反比例吗?为什么?
(2)如果要20天生产完这批豆浆机,平均每天生产多少台?
辨识成正比例的量与成反比例的量
考点03
平均每天产量/台 200 300 500
所需时间/天 75 50 30
三、典例精讲
点评
解答
本题考查了判断两个相关联的量之间成
什么比例的方法,结合题意分析解答即
可。
解:(1)因为200×75=15000
300×50=15000
500×30=15000
所以平均每天产量×所需时间=15000(一定),乘积一定,所以平均每天产量和所需时间成反比例。
(2)15000÷20=750(台)
答:平均每天产量至少要达到750台。
辨识成正比例的量与成反比例的量
考点03
三、典例精讲
分析
变式②
(1)两个相关联的量,若两个量的
比值一定,两个量成正比例关系;若
两个量的乘积一定,两个量成反比例
关系,据此判断即可。
(2)根据表中数据先求出1分钟生产
的数量,再乘36即可。
辨识成正比例的量与成反比例的量
考点03
一条生产线每3分钟自动记录一次生产产品的总数量,下面是生产产品
情况的记录。
(1)生产产品的时间和产品数量成 比例。
(2)照这样计算,36分钟生产产品多少个?
时间/分 3 6 9 12 ……
产品数量/个 51 102 153 204 ……
三、典例精讲
点评
解答
本题考查正、反比例的意义与辨识,
及正比例的应用。
辨识成正比例的量与成反比例的量
考点03
解:(1)51÷3=17
102÷6=17
153÷9=17
204÷12=17
生产产品的时间和产品数量的比值一定,所以生产产品的时间和产品数量成正比例。
(2)51÷3×36
=17×36
=612(个)
答:照这样计算,36分钟生产产品612个。
故答案为:正。
三、典例精讲
分析
变式③
(1)判断两种量成正比例还是成反
比例时,关键看这两种相关联的量中
相对应的两个数是比值一定还是乘积
一定。如果比值一定,就成正比例;
如果乘积一定,就成反比例;如果比
值和乘积都不是定量,就不成比例。
(2)求注水高度是18cm时,大约
需要的时间,用18÷每分钟注水的高
度即可解答;求注水6.5分钟注水的
高度,用6.5×每分钟注水的高度即
可解答。
辨识成正比例的量与成反比例的量
考点03
给水池注水,注水的高度与时间之间的关系如图。
(1)根据图像判断,注水高度和时间成 关系。
(2)根据图像估计一下,注水高度是18cm时,大约需要 分钟;
注水6.5分钟,注水高度大约是 cm。
三、典例精讲
点评
解答
此题考查了辨识成正比例的量与成反
比例的量,要求学生掌握。
解:(1)4÷1=4(厘米/分)
8÷2=4(厘米/分)
12÷3=4(厘米/分)
16÷4=4(厘米/分)
20÷5=4(厘米/分)
24÷6=4(厘米/分)
28÷7=4(厘米/分)
32÷8=4(厘米/分)
……
所以注水高度和时间成正比例关系。
(2)18÷4=4.5(分钟)
6.5×4=26(厘米)
答:注水高度是18cm时,大约需要4.5分钟,注水6.5分钟,注水高度大约是26厘米。
故答案为:(1)正比例;(2)4.5,26。
辨识成正比例的量与成反比例的量
考点03
谢谢观看~
第四单元 正比例与反比例
六年级下册 北师大版
一、知识导图
二、考点梳理
知识点① 变化的量
相关联的两个量,一个量随另一个量的变化而变化。
二、考点梳理
知识点② 正比例
两个相关联的量,一个量随另一个量的变化而变化,且这两个量的比值(也就是商)
一定,我们就说这样的两个量成正比例。
二、考点梳理
知识点③ 正比例的图象
1.正比例的图象是一条直线。
2.判断某一点在不在这条直线上,要看这个点所对应的两个数的比值与原成正比例
的两个量的比值是否相等,相等就在这条直线上,否则不在。
二、考点梳理
知识点④ 反比例
两个相关联的量,一个量随另一个量的变化而变化,且这两个量的乘积一定,我们
就说这样的两个量成反比例。
三、典例精讲
分析
典例01
先用男生人数加上女生人数,求出总
人数,用男生人数除以总人数就是男
生人数是全部人数的几分之几;先用
女生人数减去男生人数去求出男生比
女生少多少人,再除以女生人数就是
男生人数比女生少几分之几;写出女
生人数与全部人数的对应比,然后再
化简即可。
比的意义
考点01
解答
点评
解答此题的关键是要找准单位”1“的
量。
学校合唱队中男生有10人,女生有40人,男生人数是全部人数的
,男生人数比女生少 ,女生人数与全部人数的比是 。
解:10+40=50(人),10÷50=
(40﹣10)÷40=30÷40=
40:50=(40÷10):(50÷10)=4:5
答:男生人数是全部人数的 ,男生人数比女生少 ,女生人数与全
部人数的比是 4:5。
故答案为:4:5。
三、典例精讲
分析
变式①
由“大小两个圆的半径比是2:1”,
设小圆的半径为r,则大圆的半径为2r,
分别代入圆的面积公式S=πr2,表示
出各自的面积,再写出相应的比即可.
比的意义
考点01
解答
点评
本题主要是灵活利用圆的面积公式S
=πr2解决问题.
大小两个圆的半径比是2:1,那么大小两个圆的面积的比是 .
解:小圆的面积=πr2,
大圆的面积=π(2r)2=4πr2,
πr2:4πr2=1:4;
答:大小两个圆的面积的比是4:1.
故答案为:4:1.
三、典例精讲
分析
变式②
酒精度52%表示酒精占这瓶酒的52%,
把百分数化成分数,即是酒精占这瓶酒
的几分之几,然后计算酒精和水的比。
比的意义
考点01
解答
点评
此题主要考查了比的意义以及比与分
数的关系,要熟练掌握。
白酒中含有酒精和水,一种500毫升的白酒瓶上标注着“酒精度52%”,
这种白酒中酒精和水的比是 ,酒精占这瓶酒的 。
解:52%= ,即酒精占这瓶酒的 ;
这种白酒中酒精和水的比:13:(25﹣13)=13:12
故答案为:13:12; 。
三、典例精讲
分析
变式③
要求男生人数是女生的几倍,也就是
求25是20的几倍,用除法计算;根
据男生25人,女生20人,可知总人
数为(25+20)人,进而写出各比并
化简比即可;用男生人数减女生人数,
再除以男生人数即可。
比的意义
考点01
解答
点评
解决此题要注意比的前后项分别是哪
一个量,要对应好具体的数量,写出
比再根据比的性质把比化成最简比;
也考查了求一个数是另一个数的几倍
(或几分之几)的解答方法。
一班有男生25人,女生20人。男生人数是女生的 倍,女生人数与
男生人数的最简单的整数比是( : ),女生人数占总人数
的 ,女生人数比男生少 %。
解:25÷20=
20:25=(20÷5):(25÷5)=4:5,20+25=45(人)
20÷45= = ,(25﹣20)÷25=5÷25=20%
答:男生人数是女生的 倍,女生人数与男生人数的最简单的整数比是
4:5,女生人数占总人数的 ,女生人数比男生少20%。
故答案为: ;4;5; ;20。
三、典例精讲
分析
典例02
(1)先求出甲车行驶的时间,再根
据速度=路程÷时间,列式解答。
(2)根据乙的行车轨迹,可以知道
路程和时间成正比例关系,因为路程
是随着时间的变化而变化。
正比例和反比例的意义
考点02
甲乙两车从A地开往B地,在同一条公路上行驶,情况如图所示。
(1)甲车先慢后快,它的平均速度是每小时多少千米?
(2)根据乙的行车轨迹,可以知道哪两种量存在怎样的比例关系?为什么?
三、典例精讲
点评
解答
此题考查了行程问题的知识,解题的
关键是知道速度=路程÷时间,要求
学生掌握。
正比例和反比例的意义
考点02
解:(1)9:30﹣7:00=2:30
2时30分=2.5小时
180÷2.5=72(千米/时)
答:它的平均速度是每小时72千米。
(2)根据乙的行车轨迹,可以知道路程和时间成正比例关系,因为路
程是随着时间的变化而变化。
三、典例精讲
分析
变式①
(1)看图即可找出800千米相对应
的时间;
(2)根据正比例的意义和反比例的
意义进行解答即可:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;
(3)因为这列动车行驶的时间和路
程成正比例,可设4.5小时行驶x千米,
列比例式为x:4.5=200:1,解答
即可.
正比例和反比例的意义
考点02
一列动车在高速铁路上行驶的时间和路程如图.看图填写:
(1)这列动车行800千米需要 小时.
(2)这列动车行驶的时间和路程成 比例.
(3)照这样计算,4.5小时行驶 千米.
三、典例精讲
点评
解答
解答此题的关键是:看两种相关联量
成什么比例关系,要看比值一定还是
乘积一定,如乘积一定,则两种量成
反比例;如比值一定,则两种量成正
比例;同时考查了分析统计图以及据
此解决问题的能力.
正比例和反比例的意义
考点02
解:(1)这列动车行800千米需要4小时.
(2)400÷2=200,800÷4=200,…
因为;行驶的路程与时间的比值一定,
所以:这列动车行驶的时间和路程成正比例.
(3)设4.5小时行驶x千米,
x:4.5=200:1
2x=4.5×400
x=900
答:4.5小时行驶900千米.
故答案为:4,正,900.
三、典例精讲
分析
变式②
如果a和b成正比例,比值一定,利
用5:0.4求出比值,再利用8除以比
值即可;如果a和b成反比例,那么
乘积一定,利用5×0.4求出积再除以
8即可。
正比例和反比例的意义
考点02
如图中,如果a和b成正比例,空格处应填 ;如果a和b成反比
例,空格处应填 。
a 5 8
b 0.4
点评
解答
此题属于辨识两种相关联的量成什么
比例,就看这两种量是对应的比值一
定,还是对应的乘积一定。
解:8÷(5÷0.4)=8÷12.5=0.64
5×0.4÷8=2÷8=0.25
因此如果a和b成正比例,空格处应填0.64;如果a和b成反比例,空格处
应填0.25。
故答案为:0.64,0.25。
三、典例精讲
分析
变式③
(1)张叔叔骑自行车的路程与时间
成正比例。因为路程÷时间=速度,
速度一定。
正比例和反比例的意义
考点02
张叔叔骑自行车的时间与路程如下表所示。
(1)张叔叔骑自行车的路程与时间成正比例吗?为什么?
(2)先根据上表描点,再顺次连接。
(3)点(6,1.2)在这条直线上吗?这一点表示什么含义?
时间/分 0 1 2 3 4 5
路程/千米 0 0.2 0.4 0.6 0.8 1
三、典例精讲
点评
解答
此题考查了正比例的应用知识,要求
学生掌握。
列竖式计算除法
考点02
解:(1)0.2÷1=0.2(千米/分)
0.4÷2=0.2(千米/分)
0.6÷3=0.2(千米/分)
0.8÷4=0.2(千米/分)
1÷5=0.2(千米/分)
速度一定,所以张叔叔骑自行车的
路程与时间成正比例。
(2)
(3)点(6,1.2)在这条直线上,这一点表示张叔叔骑自行车6分钟,
走了1.2千米的路程。
三、典例精讲
分析
典例03
(1)根据图示可知30秒出水12升,出水
22升需要55秒;
(2)因为出水量除以时间一定,即相对
应的两个数的比值(商)一定,所以成正
比例;
(3)因为出水量和打开时间成正比例,
但每秒出水量比甲水龙头多,所以在甲的
图像上面即可。
右图是甲水龙头打开后出水量情况统计。
(1)根据图像填表。
(2)甲水龙头打开的时间和出水量成 比例。
(3)还有一个乙水龙头,它的出水量和打开时间成正比例,但每秒出水量比甲水龙头多,请在上图中用图像表示出乙水龙头的出水情况。
辨识成正比例的量与成反比例的量
考点03
时间/秒 30
出水量/升 22
三、典例精讲
点评
解答
此题属于根据正、反比例的意义,辨识两
种相关联的量是否成正、反比例,关键是
看这两种相关量中相对应的两个数是商一
定还是积一定,如果商一定,就成正比例;
如果积一定,就成反比例。
解:(1)如下表所示:
(2)因为12÷30=22÷55=0.4(升/秒),即相对应的两个数的比值
(商)一定,所以成正比例。
(3)如下图所示:
故答案为:55;12;正。
辨识成正比例的量与成反比例的量
考点03
时间/秒 30 55
出水量/升 12 22
三、典例精讲
分析
变式①
(1)判断两个相关联的量之间成什么
比例,就看这两个量是对应的比值一定,
还是对应的乘积一定,如果是比值一定,
就成正比例,如果是乘积一定,则成反
比例;
(2)因为平均每天产量和所需时间成
反比例,总台数不变,用总台数除以需
要的天数即可解答。
豆浆是中国人民喜爱的一种饮品,又是一种老少皆宜的营养食品,在欧
美享有“植物奶”的美誉、某工厂要生产一批豆浆机,平均每天产量和
所需时间如表。
(1)平均每天产量与所需时间成反比例吗?为什么?
(2)如果要20天生产完这批豆浆机,平均每天生产多少台?
辨识成正比例的量与成反比例的量
考点03
平均每天产量/台 200 300 500
所需时间/天 75 50 30
三、典例精讲
点评
解答
本题考查了判断两个相关联的量之间成
什么比例的方法,结合题意分析解答即
可。
解:(1)因为200×75=15000
300×50=15000
500×30=15000
所以平均每天产量×所需时间=15000(一定),乘积一定,所以平均每天产量和所需时间成反比例。
(2)15000÷20=750(台)
答:平均每天产量至少要达到750台。
辨识成正比例的量与成反比例的量
考点03
三、典例精讲
分析
变式②
(1)两个相关联的量,若两个量的
比值一定,两个量成正比例关系;若
两个量的乘积一定,两个量成反比例
关系,据此判断即可。
(2)根据表中数据先求出1分钟生产
的数量,再乘36即可。
辨识成正比例的量与成反比例的量
考点03
一条生产线每3分钟自动记录一次生产产品的总数量,下面是生产产品
情况的记录。
(1)生产产品的时间和产品数量成 比例。
(2)照这样计算,36分钟生产产品多少个?
时间/分 3 6 9 12 ……
产品数量/个 51 102 153 204 ……
三、典例精讲
点评
解答
本题考查正、反比例的意义与辨识,
及正比例的应用。
辨识成正比例的量与成反比例的量
考点03
解:(1)51÷3=17
102÷6=17
153÷9=17
204÷12=17
生产产品的时间和产品数量的比值一定,所以生产产品的时间和产品数量成正比例。
(2)51÷3×36
=17×36
=612(个)
答:照这样计算,36分钟生产产品612个。
故答案为:正。
三、典例精讲
分析
变式③
(1)判断两种量成正比例还是成反
比例时,关键看这两种相关联的量中
相对应的两个数是比值一定还是乘积
一定。如果比值一定,就成正比例;
如果乘积一定,就成反比例;如果比
值和乘积都不是定量,就不成比例。
(2)求注水高度是18cm时,大约
需要的时间,用18÷每分钟注水的高
度即可解答;求注水6.5分钟注水的
高度,用6.5×每分钟注水的高度即
可解答。
辨识成正比例的量与成反比例的量
考点03
给水池注水,注水的高度与时间之间的关系如图。
(1)根据图像判断,注水高度和时间成 关系。
(2)根据图像估计一下,注水高度是18cm时,大约需要 分钟;
注水6.5分钟,注水高度大约是 cm。
三、典例精讲
点评
解答
此题考查了辨识成正比例的量与成反
比例的量,要求学生掌握。
解:(1)4÷1=4(厘米/分)
8÷2=4(厘米/分)
12÷3=4(厘米/分)
16÷4=4(厘米/分)
20÷5=4(厘米/分)
24÷6=4(厘米/分)
28÷7=4(厘米/分)
32÷8=4(厘米/分)
……
所以注水高度和时间成正比例关系。
(2)18÷4=4.5(分钟)
6.5×4=26(厘米)
答:注水高度是18cm时,大约需要4.5分钟,注水6.5分钟,注水高度大约是26厘米。
故答案为:(1)正比例;(2)4.5,26。
辨识成正比例的量与成反比例的量
考点03
谢谢观看~
