八年级数学下册试题 第二十章 《一次函数》单元测试卷-沪教版(含解析)
文档属性
| 名称 | 八年级数学下册试题 第二十章 《一次函数》单元测试卷-沪教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览





文档简介
第二十章 《一次函数》
一、选择题(每小题4分,共24分)
1.下列四个函数中,y随x的增大而减小的是( )
A.y=3x B.y=1+2x C.y=1﹣2x D.y=﹣1+x
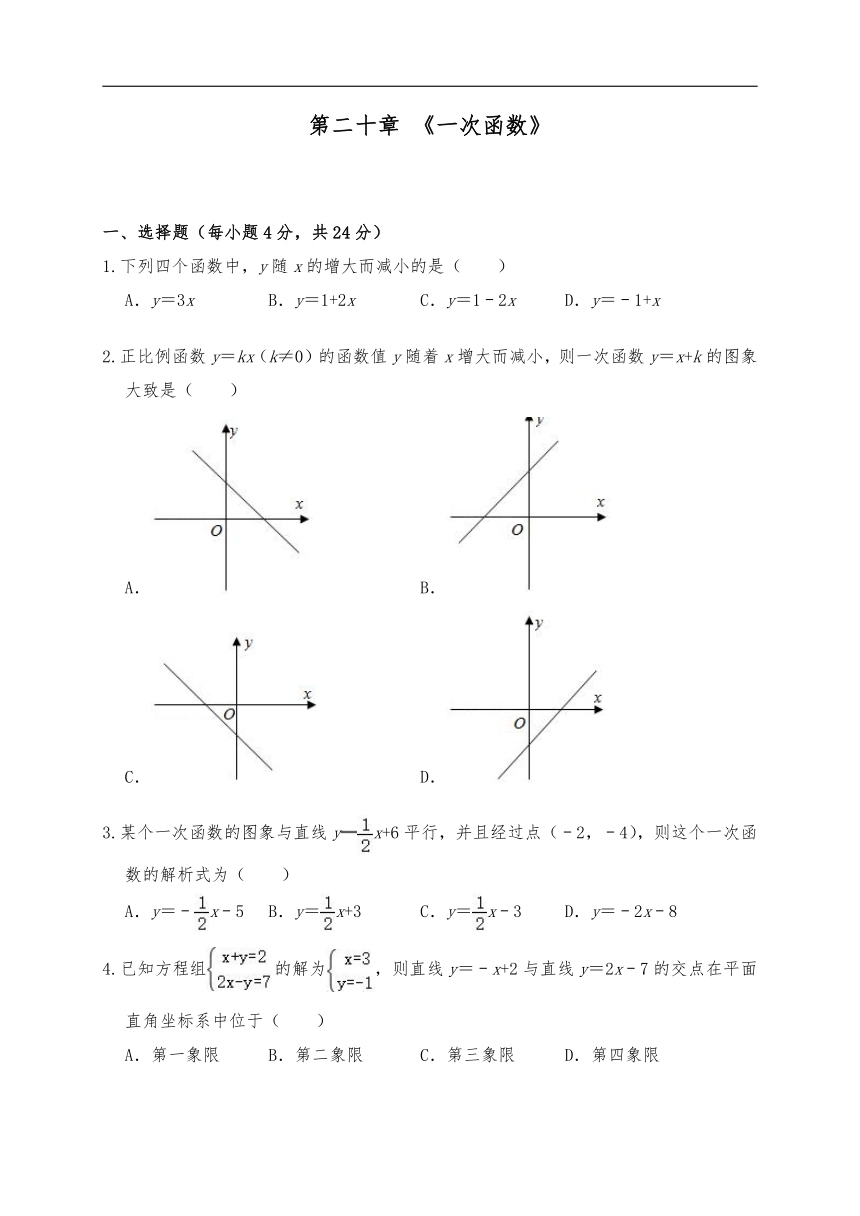
2.正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
3.某个一次函数的图象与直线y═x+6平行,并且经过点(﹣2,﹣4),则这个一次函数的解析式为( )
A.y=﹣x﹣5 B.y=x+3 C.y=x﹣3 D.y=﹣2x﹣8
4.已知方程组的解为,则直线y=﹣x+2与直线y=2x﹣7的交点在平面直角坐标系中位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知梯形ABCD的四个顶点的坐标分别是A(﹣1,0)、B(4,0)、C(3,5)、D(0,5),直线y=﹣3x+b将梯形分成面积相等的两部分,则b的值为( )
A.5 B. C.7 D.
6.如图,一次函数l:y=﹣x+2的图象与x轴、y轴分别交于A、B两点,以A为直角顶点在第一象限作等腰直角三角形ABC,则直线BC的解析式是( )
A. B. C. D.
二、填空题(每小题4分,共48分)
7.若关于x的一次函数y=kx+b的图象经过点A(﹣1,0),则方程k(x+2)+b=0的解为 .
8.点P(a,b)在函数y=3x+2的图象上,则代数式3a﹣b+1的值等于 .
9.已知一次函数的图象过点(3,5)与点(﹣4,﹣9),则这个一次函数的解析式为 .
10.如果点A(1,m)与点B(3,n)都在直线y=﹣2x+1上,那么m与n的大小关系是 .
11.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式kx+6>x+b的解集是 .
12.若二次函数y=x2﹣2x﹣m与x轴没有交点,则关于x的一次函数y=(m+1)x+m﹣1的图象不经过第 象限.
13.已知一次函数y=2x+b和y=kx﹣3(k≠0)的图象相交于点P(4,﹣6),则二元一次方程组的解是 .
14.当直线y=(2﹣2k)x+k﹣3经过第一、三、四象限时,则k的取值范围是 .
15.如图,一次函数y=kx+b与y=﹣x+4的图象相交于点P(m,1),则关于x、y的二元一次方程组的解是 .
16.甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰相距40km.
17.如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是 .
18.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.
三、解答题(共78分)
19.已知y=y1+y2,且y1与x成反比例,y2与x﹣2成正比例,当x=1时,y=1;当x=﹣3时,y=13,求:
(1)y与x之间的函数解析式;
(2)当x=3时,求y的值.
20.已知点(﹣4,2)在正比例函数y=kx的图象上.
(1)求该正比例函数的解析式;
(2)若点(﹣1,m)在该函数的图象上,求出m的值.
21.某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
22.小明同学骑自行车从家里出发依次去甲、乙两个景点游玩,他离家的距离y(km)与所用的时间x(h)之间的函数图象如图所示:
(1)甲景点与乙景点相距 千米,乙景点与小明家距离是 千米;
(2)当0≤x≤1时,y与x的函数关系式是 ;
(3)小明在游玩途中,停留所用时间为 小时,在6小时内共骑行 千米.
23.如图,在平面直角坐标系xOy中,直线l1:y=kx﹣1与直线l2:y=x+2交于点A(m,1).
(1)求m的值和直线l1的表达式;
(2)设直线l1,l2分别与y轴交于点B,C,求△ABC的面积;
(3)结合图象,直接写出不等式0<kx﹣1<x+2的解集.
24.某市为创建“全国文明城市”,计划购买甲、乙两种树苗绿化城区,购买50棵甲种树苗和20棵乙种树苗需要5000元,购买30棵甲种树苗和10棵乙种树苗需要2800元.
(1)求购买的甲、乙两种树苗每棵各需要多少元.
(2)经市绿化部门研究,决定用不超过42000元的费用购买甲、乙两种树苗共500棵,其中乙种树苗的数量不少于甲种树苗数量的,求甲种树苗数量的取值范围.
(3)在(2)的条件下,如何购买树苗才能使总费用最低?
25.如图,已知直线l的解析式为:y=x+4,它的图象与x轴、y轴分别交于A、B两点.
(1)求A、B两点的坐标及线段AB的长度;
(2)已知y轴上一点C的坐标为(0,m).
①若S△ABC=6,求点C的坐标;
②若点C到直线l与到x轴的距离相等,请直接写出点C的坐标.
答案
一、选择题
1.C
【分析】根据k小于零时,y随x的增大而减小,可得答案.
【解答】解:A、k=3>0,y随x的增大而增大,故A不符合题意;
B、k=2>0,y随x的增大而增大,故B不符合题意;
C、k=﹣2<0,y随x的增大而减小,故C符合题意;
D、k=1>0,y随x的增大而增大,故C不符合题意;
故选:C.
2.D
【分析】根据自正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x+k的图象经过第一、三、四象限.
【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,
∴k<0,
∵一次函数y=x+k的一次项系数大于0,常数项小于0,
∴一次函数y=x+k的图象经过第一、三、四象限,
故选:D.
3.C
【分析】根据两直线平行时k的值相等,设出所求解析式,把已知点坐标代入计算即可.
【解答】解:由一次函数的图象与直线y═x+6平行,设直线解析式为y=x+b,
把(﹣2,﹣4)代入得:﹣4=﹣1+b,即b=﹣3,
则这个一次函数解析式为y=x﹣3.
故选:C.
4.D
【分析】要求两直线的交点,就是联立解析式构成的方程组的解.
【解答】解:∵方程组的解为,
∴直线y=﹣x+2与直线y=2x﹣7的交点坐标为(3,﹣1),
∵x=3>0,y=﹣1<0,
∴交点在第四象限.
故选:D.
5.C
【分析】由梯形ABCD的四个顶点的坐标求出AB=5,CD=3,根据题意得出E点的坐标为:(,5),F点的坐标为:(,0),计算出DE=,AF=1+,由梯形AFED的面积=梯形ABCD的面积,得出方程,解方程即可得出结果;
【解答】解:如图,∵梯形ABCD的四个顶点的坐标分别是A(﹣1,0)、B(4,0)、C(3,5)、D(0,5),
∴AB=5,CD=3,
∵直线y=﹣3x+b与线段CD、AB交于点E、F,
∴E点的坐标为:(,5),F点的坐标为:(,0),
∴DE=,AF=1+,
∵直线y=﹣3x+b平分梯形ABCD的面积,
∴梯形AFED的面积=梯形ABCD的面积,
即:(DE+AF) h=(DC+AB) h,
∴(+1+)=(3+5),
整理得:2b=14,
∴b=7,
故选:C.
6.D
【分析】先根据一次函数的解析式求出A、B两点的坐标,再作CE⊥x轴于点E,由全等三角形的判定定理可得出△ABO≌△CAE,得出C点坐标,用待定系数法即可求出直线BC的解析式.
【解答】解:∵一次函数y=﹣x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
若∠BAC=90°,如图,作CE⊥x轴于点E,
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:,
解得,
∴直线BC的解析式是y=x+2.
故选:D.
二、填空题
7.-3
【分析】把点A(﹣1,0)代入y=kx+b,求得b=k,所以方程变为k(x+2)+k=0,即可求得方程的解.
【解答】解:∵关于x的一次函数y=kx+b的图象经过点A(﹣1,0),
∴﹣k+b=0,
∴b=k,
∴方程k(x+2)+b=0化为方程k(x+2)+k=0,
∴k(x+3)=0,
∴x=﹣3.
故答案为﹣3.
8.-1
【分析】把P(a,b)代入一次函数解析式得到b=3a+2,然后把b=3a+2代入3a﹣b+1后进行整式的加减运算即可.
【解答】解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
∴3a﹣b+1=3a﹣(3a+2)+1=3a﹣3a﹣2+1=﹣1.
故答案为﹣1.
9.y=2x-1
【分析】把两点代入函数解析式得到一二元一次方程组,求解即可得到k、b的值,函数解析式即可得到.
【解答】解:设一次函数为y=kx+b(k≠0),
因为它的图象经过(3,5),(﹣4,﹣9),
所以
解得:,
所以这个一次函数为y=2x﹣1,
故答案为y=2x﹣1.
10.m>n
【分析】将点A,点B坐标代入解析式可求m,n的值,即可求解.
【解答】解:∵点A(1,m)与点B(3,n)都在直线y=﹣2x+1上,
∴m=﹣2×1+1=﹣1,n=﹣2×3+1=﹣5,
∴m>n,
故答案为:m>n.
11.x<3
【分析】观察函数图象得到当x<3时,函数y=kx+6的图象都在y=x+b的图象上方,所以关于x的不等式kx+6>x+b的解集为x<3.
【解答】解:当x<3时,kx+6>x+b,
即不等式kx+6>x+b的解集为x<3.
故答案为:x<3.
12.一
【分析】先根据判别式的意义得到△=(﹣2)2﹣4(﹣m)<0,解得m<﹣1,然后根据一次函数的性质进行判断.
【解答】解:∵二次函数y=x2﹣2x﹣m与x轴无交点,
∴△=(﹣2)2﹣4(﹣m)<0,解得m<﹣1,
∵m+1<0,m﹣1<0,
∴一次函数y=(m+1)x+m﹣1的图象经过第二、三、四象限,不经过第一象限.
故答案为:一.
13.【分析】两个一次函数的交点坐标为P(4,﹣6),那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
【解答】解:∵一次函数y=2x+b和y=kx﹣3(k≠0)的图象交于点P(4,﹣6),
∴点P(4,﹣6)满足二元一次方程组,
∴方程组的解是.
故答案为.
14.k<1
【分析】根据一次函数y=kx+b,k>0,b<0时图象经过第一、三、四象限,可得2﹣2k>0,k﹣3<0,即可求解.
【解答】解:∵y=(2﹣2k)x+k﹣3经过第一、三、四象限,
∴.
解得k<1.
故答案是:k<1.
15.先利用y=﹣x+4确定P点坐标,然后根据方程组的解就是两个相应的一次函数图象的交点坐标进行判断.
【解答】解:把P(m,1)代入y=﹣x+4得﹣m+4=1,解得m=3,
所以P点坐标为(3,1),
所以关于x、y的二元一次方程组的解是.
故答案为.
16.①②④
【分析】根据题意和函数图象中的数据,可以判断各个小题中的说法是否正确,本题得以解决.
【解答】解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
,得,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
17.【分析】分类讨论:当PC∥OA时,△BPC∽△BOA,易得P点坐标为(0,3);当PC∥OB时,△ACP∽△ABO,易得P点坐标为(4,0);当PC⊥AB时,如图,由于∠CAP=∠OAB,则Rt△APC∽Rt△ABC,计算出AB、AC,则可利用比例式计算出AP,于是可得到OP的长,从而得到P点坐标.
【解答】解:当PC∥OA时,△BPC∽△BOA,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CAP=∠OAB,
∴Rt△APC∽Rt△ABO,
∴=,
∵点A(8,0)和点B(0,6),
∴AB==10,
∵点C是AB的中点,
∴AC=5,
∴=,
∴AP=,
∴OP=OA﹣AP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0)
18.12
【分析】首先确定甲乙两人的速度,求出总里程,再求出甲到达B地时,乙离B地的距离即可解决问题.
【解答】解:由题意乙的速度为1500÷5=300(米/分),设甲的速度为x米/分.
则有:7500﹣20x=2500,
解得,x=250,
25分钟后甲的速度为250×=400(米/分).
由题意总里程=250×20+61×400=29400(米),
86分钟乙的路程为86×300=25800(米),
∴=12(分钟).
故答案为:12.
三、解答题
19.解:(1)根据题意设y1=,y2=b(x﹣2),即y=y1+y2=+b(x﹣2),
将x=1时,y=1;x=﹣3时,y=13分别代入得:,
解得:k=﹣,b=﹣,
则y=﹣﹣(x﹣2);
(2)当x=3时,y=﹣﹣=﹣3.
20.解:(1)∵点(﹣4,2)在正比例函数y=kx的图象上,
∴﹣4k=2,
∴k=﹣;
∴该正比例函数的解析式为y=﹣x;
(2)∵点(﹣1,m)在函数y=﹣x的图象上,
∴m=﹣×(﹣1),
∴m=.
21.解:(1)设该店11月份购进甲种水果x千克,购进乙种水果y千克,
根据题意得:,
解得,
答:该店5月份购进甲种水果100千克,购进乙种水果50千克;
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,
根据题意得:w=10a+20(120﹣a)=﹣10a+2400;
(3)根据题意得,a≤90,由(2)得,w=﹣10a+2400,
∵﹣10<0,w随a的增大而减小,
∴a=90时,w有最小值w最小=﹣10×90+2400=1500(元).
答:12月份该店需要支付这两种水果的货款最少应是1500元.
22.解:(1)由图象可得,
甲景点与乙景点相距:12﹣6=6(千米);
乙景点与小明家距离是12千米;
故答案为:6;12;
(2)当0≤x≤1时,设y与x的函数关系式y=kx,根据题意,
得k=6,
所以y=6x(0≤x≤1);
故答案为:y=6x;
(3)由图象可得,
小明在游玩途中,停留所用时间为:3﹣1+(5﹣4)=3(小时);
小明在6小时内共骑行:12×2=24(千米),
故答案为:3;24.
23.解:(1)把A(m,1)代入y=x+2得m+2=1,解得m=﹣2,
∴A(﹣2,1),
把A(﹣2,1)代入y=kx﹣1得﹣2k﹣1=1,解得k=﹣1,
∴直线l1的表达式为y=﹣x﹣1;
(2)当x=0时,y=x+2=2,则C(0,2);
当x=0时,y=﹣x﹣1=﹣1,则B(0,﹣1),
∴△ABC的面积=×(2+1)×2=3;
(3)当y=0时,﹣x﹣1=0,解得x=﹣1,
∴直线y=﹣x﹣1与x轴的交点坐标为(﹣1,0),
当﹣2<x<﹣1时,0<kx﹣1<x+2,
即不等式0<kx﹣1<x+2的解集为﹣2<x<﹣1.
24.解:(1)设购买的甲种树苗的单价为x元,乙种树苗的单价为y元.依题意得:
,
解这个方程组得:,
答:购买的甲种树苗的单价是60元,乙种树苗的单价是100元;
(2)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,由题意得,
,
解得,200≤a≤400.
∴甲种树苗数量a的取值范围是200≤a≤400.
(3)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,总费用为W,
∴W=60a+100(500﹣a)=50000﹣40a.
∵﹣40<0,
∴W值随a值的增大而减小,
∵200≤a≤400,
∴当x=400时,W取最小值,最小值为50000﹣40×400=34000元.
即购买的甲种树苗400棵,购买乙种树苗100棵,总费用最低.
25.解:(1)当y=0时,x+4=0,解得:x=﹣3,
∴点A的坐标为(﹣3,0);
当x=0时,y=×0+4=4,
∴点B的坐标为(0,4).
在Rt△AOB中,OA=3,OB=4,∠AOB=90°,
∴AB==5.
(2)①∵S△ABC=6,
∴OA BC=6,即×3BC=6,
∴BC=4,
又∵点B的坐标为(0,4),
∴点C的坐标为(0,8)或(0,0).
②当点C1在∠BAO的平分线上时,过点C1作C1D⊥直线l于点D,则C1D=OC1,如图所示.
∵=OA OC1=OA C1D,=AB C1D=OA BC1,
∴==,即=,
∴OC1=,
∴点C1的坐标为(0,);
当点C2在∠BAO外角的平分线上时,∠C1AC2=90°.
∵∠C1AO+∠C2AO=90°,∠C1AO+∠AC1O=90°,
∴∠C2AO=∠AC1O,
∴△AOC2∽△C1OA,
∴=,即=,
∴OC2=6,
∴点C2的坐标为(0,﹣6).
∴点C的坐标为(0,)或(0,﹣6).
一、选择题(每小题4分,共24分)
1.下列四个函数中,y随x的增大而减小的是( )
A.y=3x B.y=1+2x C.y=1﹣2x D.y=﹣1+x
2.正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
C. D.
3.某个一次函数的图象与直线y═x+6平行,并且经过点(﹣2,﹣4),则这个一次函数的解析式为( )
A.y=﹣x﹣5 B.y=x+3 C.y=x﹣3 D.y=﹣2x﹣8
4.已知方程组的解为,则直线y=﹣x+2与直线y=2x﹣7的交点在平面直角坐标系中位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知梯形ABCD的四个顶点的坐标分别是A(﹣1,0)、B(4,0)、C(3,5)、D(0,5),直线y=﹣3x+b将梯形分成面积相等的两部分,则b的值为( )
A.5 B. C.7 D.
6.如图,一次函数l:y=﹣x+2的图象与x轴、y轴分别交于A、B两点,以A为直角顶点在第一象限作等腰直角三角形ABC,则直线BC的解析式是( )
A. B. C. D.
二、填空题(每小题4分,共48分)
7.若关于x的一次函数y=kx+b的图象经过点A(﹣1,0),则方程k(x+2)+b=0的解为 .
8.点P(a,b)在函数y=3x+2的图象上,则代数式3a﹣b+1的值等于 .
9.已知一次函数的图象过点(3,5)与点(﹣4,﹣9),则这个一次函数的解析式为 .
10.如果点A(1,m)与点B(3,n)都在直线y=﹣2x+1上,那么m与n的大小关系是 .
11.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式kx+6>x+b的解集是 .
12.若二次函数y=x2﹣2x﹣m与x轴没有交点,则关于x的一次函数y=(m+1)x+m﹣1的图象不经过第 象限.
13.已知一次函数y=2x+b和y=kx﹣3(k≠0)的图象相交于点P(4,﹣6),则二元一次方程组的解是 .
14.当直线y=(2﹣2k)x+k﹣3经过第一、三、四象限时,则k的取值范围是 .
15.如图,一次函数y=kx+b与y=﹣x+4的图象相交于点P(m,1),则关于x、y的二元一次方程组的解是 .
16.甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰相距40km.
17.如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是 .
18.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A地出发前往B地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达B地,乙一直保持原速前往B地.在此过程中,甲、乙两人相距的路程y(单位:米)与乙骑行的时间x(单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B地.
三、解答题(共78分)
19.已知y=y1+y2,且y1与x成反比例,y2与x﹣2成正比例,当x=1时,y=1;当x=﹣3时,y=13,求:
(1)y与x之间的函数解析式;
(2)当x=3时,求y的值.
20.已知点(﹣4,2)在正比例函数y=kx的图象上.
(1)求该正比例函数的解析式;
(2)若点(﹣1,m)在该函数的图象上,求出m的值.
21.某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
22.小明同学骑自行车从家里出发依次去甲、乙两个景点游玩,他离家的距离y(km)与所用的时间x(h)之间的函数图象如图所示:
(1)甲景点与乙景点相距 千米,乙景点与小明家距离是 千米;
(2)当0≤x≤1时,y与x的函数关系式是 ;
(3)小明在游玩途中,停留所用时间为 小时,在6小时内共骑行 千米.
23.如图,在平面直角坐标系xOy中,直线l1:y=kx﹣1与直线l2:y=x+2交于点A(m,1).
(1)求m的值和直线l1的表达式;
(2)设直线l1,l2分别与y轴交于点B,C,求△ABC的面积;
(3)结合图象,直接写出不等式0<kx﹣1<x+2的解集.
24.某市为创建“全国文明城市”,计划购买甲、乙两种树苗绿化城区,购买50棵甲种树苗和20棵乙种树苗需要5000元,购买30棵甲种树苗和10棵乙种树苗需要2800元.
(1)求购买的甲、乙两种树苗每棵各需要多少元.
(2)经市绿化部门研究,决定用不超过42000元的费用购买甲、乙两种树苗共500棵,其中乙种树苗的数量不少于甲种树苗数量的,求甲种树苗数量的取值范围.
(3)在(2)的条件下,如何购买树苗才能使总费用最低?
25.如图,已知直线l的解析式为:y=x+4,它的图象与x轴、y轴分别交于A、B两点.
(1)求A、B两点的坐标及线段AB的长度;
(2)已知y轴上一点C的坐标为(0,m).
①若S△ABC=6,求点C的坐标;
②若点C到直线l与到x轴的距离相等,请直接写出点C的坐标.
答案
一、选择题
1.C
【分析】根据k小于零时,y随x的增大而减小,可得答案.
【解答】解:A、k=3>0,y随x的增大而增大,故A不符合题意;
B、k=2>0,y随x的增大而增大,故B不符合题意;
C、k=﹣2<0,y随x的增大而减小,故C符合题意;
D、k=1>0,y随x的增大而增大,故C不符合题意;
故选:C.
2.D
【分析】根据自正比例函数的性质得到k<0,然后根据一次函数的性质得到一次函数y=x+k的图象经过第一、三、四象限.
【解答】解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,
∴k<0,
∵一次函数y=x+k的一次项系数大于0,常数项小于0,
∴一次函数y=x+k的图象经过第一、三、四象限,
故选:D.
3.C
【分析】根据两直线平行时k的值相等,设出所求解析式,把已知点坐标代入计算即可.
【解答】解:由一次函数的图象与直线y═x+6平行,设直线解析式为y=x+b,
把(﹣2,﹣4)代入得:﹣4=﹣1+b,即b=﹣3,
则这个一次函数解析式为y=x﹣3.
故选:C.
4.D
【分析】要求两直线的交点,就是联立解析式构成的方程组的解.
【解答】解:∵方程组的解为,
∴直线y=﹣x+2与直线y=2x﹣7的交点坐标为(3,﹣1),
∵x=3>0,y=﹣1<0,
∴交点在第四象限.
故选:D.
5.C
【分析】由梯形ABCD的四个顶点的坐标求出AB=5,CD=3,根据题意得出E点的坐标为:(,5),F点的坐标为:(,0),计算出DE=,AF=1+,由梯形AFED的面积=梯形ABCD的面积,得出方程,解方程即可得出结果;
【解答】解:如图,∵梯形ABCD的四个顶点的坐标分别是A(﹣1,0)、B(4,0)、C(3,5)、D(0,5),
∴AB=5,CD=3,
∵直线y=﹣3x+b与线段CD、AB交于点E、F,
∴E点的坐标为:(,5),F点的坐标为:(,0),
∴DE=,AF=1+,
∵直线y=﹣3x+b平分梯形ABCD的面积,
∴梯形AFED的面积=梯形ABCD的面积,
即:(DE+AF) h=(DC+AB) h,
∴(+1+)=(3+5),
整理得:2b=14,
∴b=7,
故选:C.
6.D
【分析】先根据一次函数的解析式求出A、B两点的坐标,再作CE⊥x轴于点E,由全等三角形的判定定理可得出△ABO≌△CAE,得出C点坐标,用待定系数法即可求出直线BC的解析式.
【解答】解:∵一次函数y=﹣x+2中,
令x=0得:y=2;令y=0,解得x=5,
∴B的坐标是(0,2),A的坐标是(5,0).
若∠BAC=90°,如图,作CE⊥x轴于点E,
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
又∵∠CAE+∠ACE=90°,
∴∠ACE=∠BAO.
在△ABO与△CAE中
,
∴△ABO≌△CAE(AAS),
∴OB=AE=2,OA=CE=5,
∴OE=OA+AE=2+5=7.
则C的坐标是(7,5).
设直线BC的解析式是y=kx+b,
根据题意得:,
解得,
∴直线BC的解析式是y=x+2.
故选:D.
二、填空题
7.-3
【分析】把点A(﹣1,0)代入y=kx+b,求得b=k,所以方程变为k(x+2)+k=0,即可求得方程的解.
【解答】解:∵关于x的一次函数y=kx+b的图象经过点A(﹣1,0),
∴﹣k+b=0,
∴b=k,
∴方程k(x+2)+b=0化为方程k(x+2)+k=0,
∴k(x+3)=0,
∴x=﹣3.
故答案为﹣3.
8.-1
【分析】把P(a,b)代入一次函数解析式得到b=3a+2,然后把b=3a+2代入3a﹣b+1后进行整式的加减运算即可.
【解答】解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
∴3a﹣b+1=3a﹣(3a+2)+1=3a﹣3a﹣2+1=﹣1.
故答案为﹣1.
9.y=2x-1
【分析】把两点代入函数解析式得到一二元一次方程组,求解即可得到k、b的值,函数解析式即可得到.
【解答】解:设一次函数为y=kx+b(k≠0),
因为它的图象经过(3,5),(﹣4,﹣9),
所以
解得:,
所以这个一次函数为y=2x﹣1,
故答案为y=2x﹣1.
10.m>n
【分析】将点A,点B坐标代入解析式可求m,n的值,即可求解.
【解答】解:∵点A(1,m)与点B(3,n)都在直线y=﹣2x+1上,
∴m=﹣2×1+1=﹣1,n=﹣2×3+1=﹣5,
∴m>n,
故答案为:m>n.
11.x<3
【分析】观察函数图象得到当x<3时,函数y=kx+6的图象都在y=x+b的图象上方,所以关于x的不等式kx+6>x+b的解集为x<3.
【解答】解:当x<3时,kx+6>x+b,
即不等式kx+6>x+b的解集为x<3.
故答案为:x<3.
12.一
【分析】先根据判别式的意义得到△=(﹣2)2﹣4(﹣m)<0,解得m<﹣1,然后根据一次函数的性质进行判断.
【解答】解:∵二次函数y=x2﹣2x﹣m与x轴无交点,
∴△=(﹣2)2﹣4(﹣m)<0,解得m<﹣1,
∵m+1<0,m﹣1<0,
∴一次函数y=(m+1)x+m﹣1的图象经过第二、三、四象限,不经过第一象限.
故答案为:一.
13.【分析】两个一次函数的交点坐标为P(4,﹣6),那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
【解答】解:∵一次函数y=2x+b和y=kx﹣3(k≠0)的图象交于点P(4,﹣6),
∴点P(4,﹣6)满足二元一次方程组,
∴方程组的解是.
故答案为.
14.k<1
【分析】根据一次函数y=kx+b,k>0,b<0时图象经过第一、三、四象限,可得2﹣2k>0,k﹣3<0,即可求解.
【解答】解:∵y=(2﹣2k)x+k﹣3经过第一、三、四象限,
∴.
解得k<1.
故答案是:k<1.
15.先利用y=﹣x+4确定P点坐标,然后根据方程组的解就是两个相应的一次函数图象的交点坐标进行判断.
【解答】解:把P(m,1)代入y=﹣x+4得﹣m+4=1,解得m=3,
所以P点坐标为(3,1),
所以关于x、y的二元一次方程组的解是.
故答案为.
16.①②④
【分析】根据题意和函数图象中的数据,可以判断各个小题中的说法是否正确,本题得以解决.
【解答】解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
,得,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
17.【分析】分类讨论:当PC∥OA时,△BPC∽△BOA,易得P点坐标为(0,3);当PC∥OB时,△ACP∽△ABO,易得P点坐标为(4,0);当PC⊥AB时,如图,由于∠CAP=∠OAB,则Rt△APC∽Rt△ABC,计算出AB、AC,则可利用比例式计算出AP,于是可得到OP的长,从而得到P点坐标.
【解答】解:当PC∥OA时,△BPC∽△BOA,
由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,
由点C是AB的中点,可得P为OA的中点,
此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵∠CAP=∠OAB,
∴Rt△APC∽Rt△ABO,
∴=,
∵点A(8,0)和点B(0,6),
∴AB==10,
∵点C是AB的中点,
∴AC=5,
∴=,
∴AP=,
∴OP=OA﹣AP=8﹣=,
此时P点坐标为(,0),
综上所述,满足条件的P点坐标为(0,3)、(4,0)、(,0).
故答案为:(0,3)、(4,0)、(,0)
18.12
【分析】首先确定甲乙两人的速度,求出总里程,再求出甲到达B地时,乙离B地的距离即可解决问题.
【解答】解:由题意乙的速度为1500÷5=300(米/分),设甲的速度为x米/分.
则有:7500﹣20x=2500,
解得,x=250,
25分钟后甲的速度为250×=400(米/分).
由题意总里程=250×20+61×400=29400(米),
86分钟乙的路程为86×300=25800(米),
∴=12(分钟).
故答案为:12.
三、解答题
19.解:(1)根据题意设y1=,y2=b(x﹣2),即y=y1+y2=+b(x﹣2),
将x=1时,y=1;x=﹣3时,y=13分别代入得:,
解得:k=﹣,b=﹣,
则y=﹣﹣(x﹣2);
(2)当x=3时,y=﹣﹣=﹣3.
20.解:(1)∵点(﹣4,2)在正比例函数y=kx的图象上,
∴﹣4k=2,
∴k=﹣;
∴该正比例函数的解析式为y=﹣x;
(2)∵点(﹣1,m)在函数y=﹣x的图象上,
∴m=﹣×(﹣1),
∴m=.
21.解:(1)设该店11月份购进甲种水果x千克,购进乙种水果y千克,
根据题意得:,
解得,
答:该店5月份购进甲种水果100千克,购进乙种水果50千克;
(2)设购进甲种水果a千克,需要支付的货款为w元,则购进乙种水果(120﹣a)千克,
根据题意得:w=10a+20(120﹣a)=﹣10a+2400;
(3)根据题意得,a≤90,由(2)得,w=﹣10a+2400,
∵﹣10<0,w随a的增大而减小,
∴a=90时,w有最小值w最小=﹣10×90+2400=1500(元).
答:12月份该店需要支付这两种水果的货款最少应是1500元.
22.解:(1)由图象可得,
甲景点与乙景点相距:12﹣6=6(千米);
乙景点与小明家距离是12千米;
故答案为:6;12;
(2)当0≤x≤1时,设y与x的函数关系式y=kx,根据题意,
得k=6,
所以y=6x(0≤x≤1);
故答案为:y=6x;
(3)由图象可得,
小明在游玩途中,停留所用时间为:3﹣1+(5﹣4)=3(小时);
小明在6小时内共骑行:12×2=24(千米),
故答案为:3;24.
23.解:(1)把A(m,1)代入y=x+2得m+2=1,解得m=﹣2,
∴A(﹣2,1),
把A(﹣2,1)代入y=kx﹣1得﹣2k﹣1=1,解得k=﹣1,
∴直线l1的表达式为y=﹣x﹣1;
(2)当x=0时,y=x+2=2,则C(0,2);
当x=0时,y=﹣x﹣1=﹣1,则B(0,﹣1),
∴△ABC的面积=×(2+1)×2=3;
(3)当y=0时,﹣x﹣1=0,解得x=﹣1,
∴直线y=﹣x﹣1与x轴的交点坐标为(﹣1,0),
当﹣2<x<﹣1时,0<kx﹣1<x+2,
即不等式0<kx﹣1<x+2的解集为﹣2<x<﹣1.
24.解:(1)设购买的甲种树苗的单价为x元,乙种树苗的单价为y元.依题意得:
,
解这个方程组得:,
答:购买的甲种树苗的单价是60元,乙种树苗的单价是100元;
(2)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,由题意得,
,
解得,200≤a≤400.
∴甲种树苗数量a的取值范围是200≤a≤400.
(3)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,总费用为W,
∴W=60a+100(500﹣a)=50000﹣40a.
∵﹣40<0,
∴W值随a值的增大而减小,
∵200≤a≤400,
∴当x=400时,W取最小值,最小值为50000﹣40×400=34000元.
即购买的甲种树苗400棵,购买乙种树苗100棵,总费用最低.
25.解:(1)当y=0时,x+4=0,解得:x=﹣3,
∴点A的坐标为(﹣3,0);
当x=0时,y=×0+4=4,
∴点B的坐标为(0,4).
在Rt△AOB中,OA=3,OB=4,∠AOB=90°,
∴AB==5.
(2)①∵S△ABC=6,
∴OA BC=6,即×3BC=6,
∴BC=4,
又∵点B的坐标为(0,4),
∴点C的坐标为(0,8)或(0,0).
②当点C1在∠BAO的平分线上时,过点C1作C1D⊥直线l于点D,则C1D=OC1,如图所示.
∵=OA OC1=OA C1D,=AB C1D=OA BC1,
∴==,即=,
∴OC1=,
∴点C1的坐标为(0,);
当点C2在∠BAO外角的平分线上时,∠C1AC2=90°.
∵∠C1AO+∠C2AO=90°,∠C1AO+∠AC1O=90°,
∴∠C2AO=∠AC1O,
∴△AOC2∽△C1OA,
∴=,即=,
∴OC2=6,
∴点C2的坐标为(0,﹣6).
∴点C的坐标为(0,)或(0,﹣6).
