4.9表面积的变化②(教学课件)五年级数学下册 沪教版(共21张PPT)
文档属性
| 名称 | 4.9表面积的变化②(教学课件)五年级数学下册 沪教版(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
4.9 表面积的变化②
小学数学·五年级(下)·HJ
利用表面积等有关知识,探索多个相同正方体叠放后表面积的变化规律,激发主动探索的欲望。
通过解决包装问题,体验策略的多样化,发展优化思想。
学习目标
能灵活运用发现的规律解决一些简单实际问题。
通过观察和实际操作,探索多个相同正(长)方体组合过程中表面积的变化规律,进一步发展动手操作能力和空间观念。
重点难点
超市里商品的包装,都有什么小秘密呢?
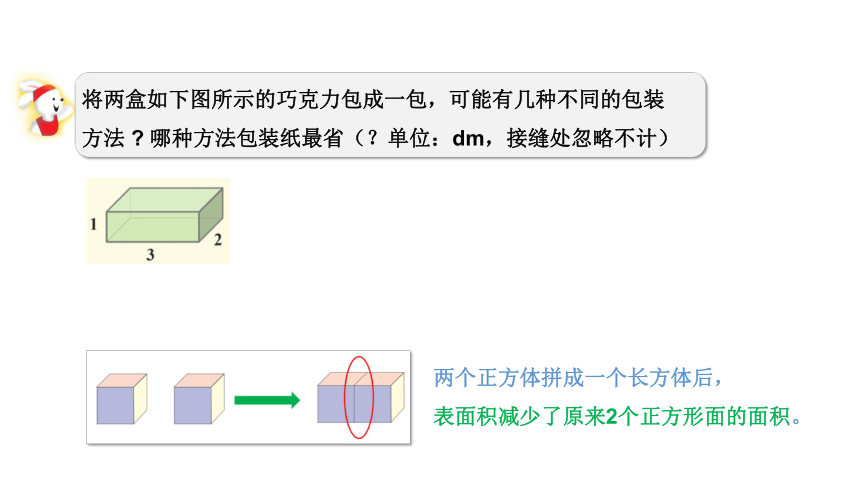
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
两个正方体拼成一个长方体后,
表面积减少了原来2个正方形面的面积。
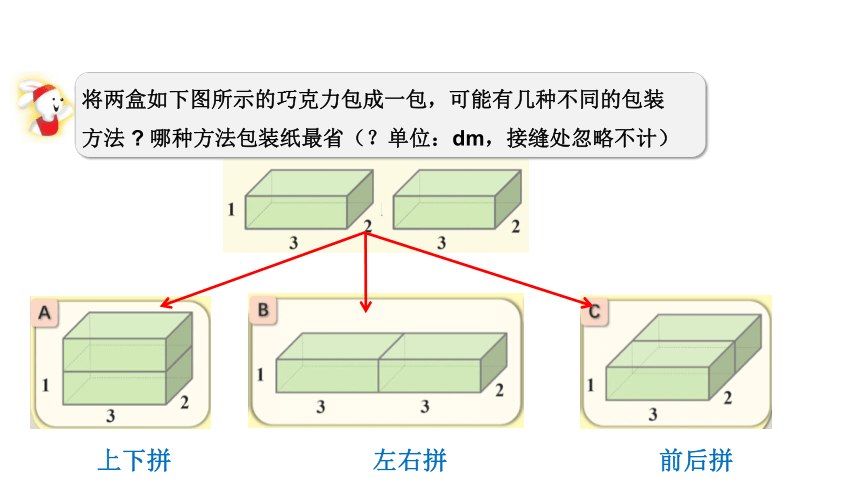
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
上下拼
左右拼
前后拼
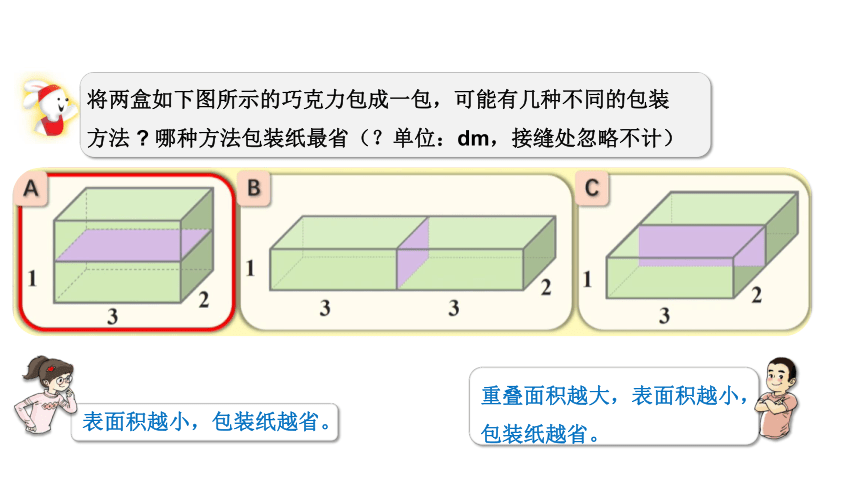
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
表面积越小,包装纸越省。
重叠面积越大,表面积越小,
包装纸越省。
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×2+3×2+2×2)
=2×16
=32(dm2)
减少的面积:
(3×2)×2=12(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(6×2+6×1+2×1)
=2×20
=40(dm2)
减少的面积:
(1×2)×2=4(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×4+3×1+4×1)
=2×19
=38(dm2)
减少的面积:
(1×3)×2=6(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×2+3×3+2×3)
=2×21
=42(dm2)
减少的面积:
(2×3)×4=24(dm2)
拼成长方体的表面积:
S=2×(3×3+3×2+3×2)
=2×21
=42(dm2)
减少的面积:
(2×3)×4=24(dm2)
将三个棱长各不相同的正方体拼成一个组合体,哪一种拼法表面积更小?
答:图2的拼法,表面积更小。
解:
宽:10.8÷2=5.4(米)
面积:5.4×(7.5+2)
=5.4×9.5
=51.3(平方米)
答:现在这个花坛的面积是51.3平方米。
解:
加工后的体积:
(6.2-0.2)×(4-0.2)×(1.3-0.2)
=6×3.8×1.1
=25.08(立方分米)
减少:6.2×4×1.3-25.08
=32.24-25.08
=7.16(立方分米)
答:加工后的体积是25.08立方分米,
比原来减少7.16立方分米。
解:2×(50×2.4+21×2.4)+50×21
=2×(120+50.4)+1050
=2×170.4+1050
=340.8+1050
=1390.8(平方米)
长:50÷0.2=250(块)
宽:21÷0.2=105(块)
深:2.4÷0.2=12(块)
共需要:
250×105+250×12×2+105×12×2
=26250+6000+2520
=34770(块)
答:一共需要贴1390.8平方米的瓷砖,至少需要瓷砖34770块。
解:两个长方体表面积之和为:
2×(1×1+1×2+1×2)×2
=2×5×2
=20(cm2)
左右拼:
20-1×2×2=16(cm2)
前后拼:
20-1×2×2=16(cm2)
上下拼:
20-1×1×2=18(cm2)
答:可能有3种情况,表面积各是16cm2、16cm2、18cm2.
4.9 表面积的变化②
1.课本P60/61;
2.练习册P61.
4.9 表面积的变化②
小学数学·五年级(下)·HJ
利用表面积等有关知识,探索多个相同正方体叠放后表面积的变化规律,激发主动探索的欲望。
通过解决包装问题,体验策略的多样化,发展优化思想。
学习目标
能灵活运用发现的规律解决一些简单实际问题。
通过观察和实际操作,探索多个相同正(长)方体组合过程中表面积的变化规律,进一步发展动手操作能力和空间观念。
重点难点
超市里商品的包装,都有什么小秘密呢?
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
两个正方体拼成一个长方体后,
表面积减少了原来2个正方形面的面积。
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
上下拼
左右拼
前后拼
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
表面积越小,包装纸越省。
重叠面积越大,表面积越小,
包装纸越省。
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×2+3×2+2×2)
=2×16
=32(dm2)
减少的面积:
(3×2)×2=12(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(6×2+6×1+2×1)
=2×20
=40(dm2)
减少的面积:
(1×2)×2=4(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×4+3×1+4×1)
=2×19
=38(dm2)
减少的面积:
(1×3)×2=6(dm2)
将两盒如下图所示的巧克力包成一包,可能有几种不同的包装
方法 哪种方法包装纸最省(?单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
将三盒这样的巧克力包成一包,可能有几种不同的包装方
法?哪种方法包装纸最省?(单位:dm,接缝处忽略不计)
拼成长方体的表面积:
S=2×(3×2+3×3+2×3)
=2×21
=42(dm2)
减少的面积:
(2×3)×4=24(dm2)
拼成长方体的表面积:
S=2×(3×3+3×2+3×2)
=2×21
=42(dm2)
减少的面积:
(2×3)×4=24(dm2)
将三个棱长各不相同的正方体拼成一个组合体,哪一种拼法表面积更小?
答:图2的拼法,表面积更小。
解:
宽:10.8÷2=5.4(米)
面积:5.4×(7.5+2)
=5.4×9.5
=51.3(平方米)
答:现在这个花坛的面积是51.3平方米。
解:
加工后的体积:
(6.2-0.2)×(4-0.2)×(1.3-0.2)
=6×3.8×1.1
=25.08(立方分米)
减少:6.2×4×1.3-25.08
=32.24-25.08
=7.16(立方分米)
答:加工后的体积是25.08立方分米,
比原来减少7.16立方分米。
解:2×(50×2.4+21×2.4)+50×21
=2×(120+50.4)+1050
=2×170.4+1050
=340.8+1050
=1390.8(平方米)
长:50÷0.2=250(块)
宽:21÷0.2=105(块)
深:2.4÷0.2=12(块)
共需要:
250×105+250×12×2+105×12×2
=26250+6000+2520
=34770(块)
答:一共需要贴1390.8平方米的瓷砖,至少需要瓷砖34770块。
解:两个长方体表面积之和为:
2×(1×1+1×2+1×2)×2
=2×5×2
=20(cm2)
左右拼:
20-1×2×2=16(cm2)
前后拼:
20-1×2×2=16(cm2)
上下拼:
20-1×1×2=18(cm2)
答:可能有3种情况,表面积各是16cm2、16cm2、18cm2.
4.9 表面积的变化②
1.课本P60/61;
2.练习册P61.
