3.1.1 椭圆及其标准方程 课件(共16张PPT)
文档属性
| 名称 | 3.1.1 椭圆及其标准方程 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 15:27:44 | ||
图片预览





文档简介
(共16张PPT)
单/击/此/处/添/加/副/标/题/内/容
椭圆及其标准方程
1 问题情境
问题1:用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢
通常把椭圆、抛物线、双曲线统称为圆锥曲线(conic sections).
问题2:历史上,古希腊人曾用纯几何的方法研究圆锥曲线.17世纪后,人们开始用坐标法研究圆锥曲线.你能猜测这些变化的大致原因吗 如果本章我们用坐标法来研究圆锥曲线,大家能在回顾用坐标法研究直线与圆的基础上,猜想研究的大致思路与构架吗
现实背景——曲线概念——曲线方程——曲线性质——实际应用
学习目标
1.能通过观察平面截圆锥认识到:当平面与圆锥的轴所成的角不同时,可以分别得到圆、椭圆、双曲线和抛物线.能通过章引言初步认识本章的学习内容、学习方法与学习价值.
2.能通过绘制椭圆的过程认识椭圆的几何特征,给出椭圆的定义,并能用它解决简单的问题,发展数学抽象素养.
3.能建立适当的坐标系得到椭圆的标准方程,并能用它解决简单的问题.体会建立曲线的方程的方法,发展直观想象、数学运算素养.
2 新知建构
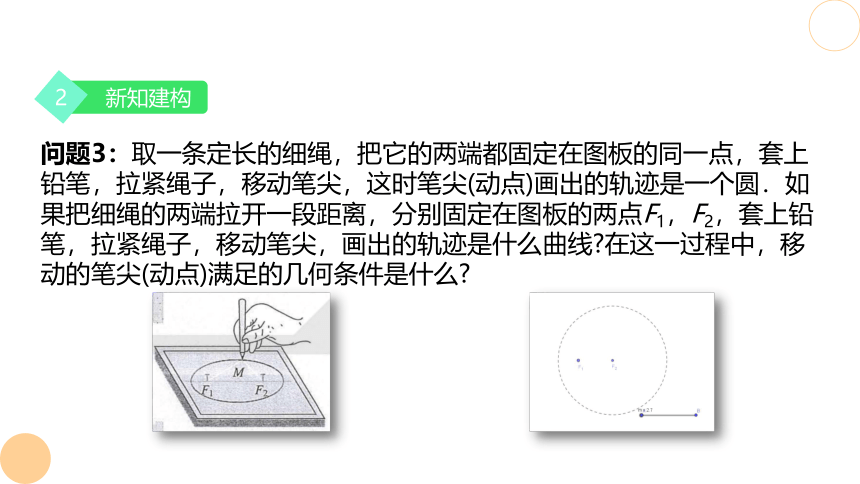
问题3:取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点F1,F2,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线 在这一过程中,移动的笔尖(动点)满足的几何条件是什么
问题4:你能用精确的数学语言刻画椭圆吗
我们把平面内与两个定点F1,F2的距离的和等于常数(大于| F1F2 |)的点的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点(focus),两焦点间的距离叫做椭圆的焦距(focus distance),焦距的一半称为半焦距.
椭圆的定义
当常数等于两定点间的距离时,点的轨迹是线段;
当常数小于两定点间的距离时,点的轨迹不存在.
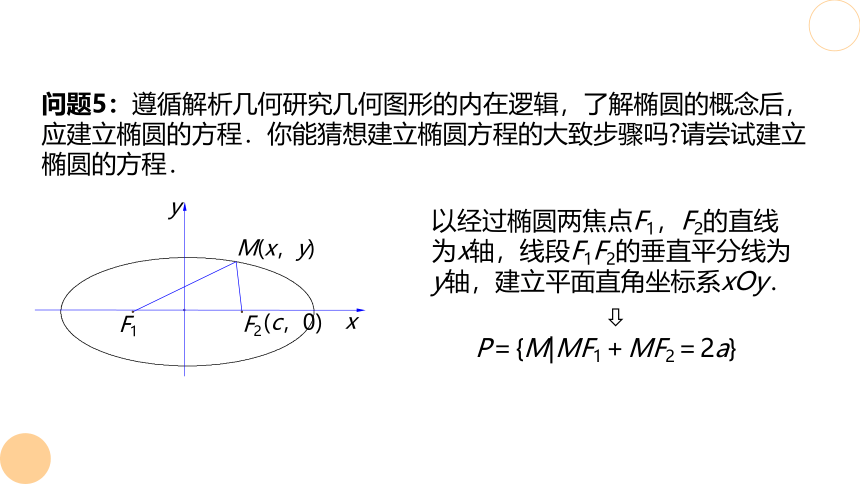
问题5:遵循解析几何研究几何图形的内在逻辑,了解椭圆的概念后,应建立椭圆的方程.你能猜想建立椭圆方程的大致步骤吗 请尝试建立椭圆的方程.
以经过椭圆两焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy.
M(x,y)
F1
F2
x
y
(c,0)
P={M|MF1+MF2=2a}
P
F1
F2
x
y
O
问题6:如果椭圆的焦点F1,F2在y轴上,且F1,F2的坐标分别为(0,-c),(0,c),a,b的意义同上,那么椭圆的方程又是什么
y
O
x
F1
F2
M
此时椭圆的方程为
这也是椭圆的标准方程.
椭圆的方程
根据椭圆的几何特征建立适当的直角坐标系
明确椭圆上的点满足的几何条件
将几何条件转化为代数表示列出方程
化简方程
检验方程
M
F1
F2
x
y
y
O
x
F1
F2
M
3 数学运用
3 数学运用
4 回顾反思
问题7:
(1)椭圆的概念中的要点与需要注意的地方分别是什么
(2)推导椭圆的标准方程时,建立直角坐标系的依据是什么
(3)椭圆标准方程的推导给了你怎样的启示 就一般情况而言,求曲线的方程有哪些步骤 为什么是这些步骤
5 学习评价
1.尝试通过其他化简方案推导椭圆的标准方程.
2.完成教科书习题3.1第1,2题.
实践:请利用细绳、铅笔,动手操作,画一个椭圆.
再 见
汇报人姓名
单/击/此/处/添/加/副/标/题/内/容
椭圆及其标准方程
1 问题情境
问题1:用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变截面与圆锥的轴所成的角,会得到怎样的截口曲线呢
通常把椭圆、抛物线、双曲线统称为圆锥曲线(conic sections).
问题2:历史上,古希腊人曾用纯几何的方法研究圆锥曲线.17世纪后,人们开始用坐标法研究圆锥曲线.你能猜测这些变化的大致原因吗 如果本章我们用坐标法来研究圆锥曲线,大家能在回顾用坐标法研究直线与圆的基础上,猜想研究的大致思路与构架吗
现实背景——曲线概念——曲线方程——曲线性质——实际应用
学习目标
1.能通过观察平面截圆锥认识到:当平面与圆锥的轴所成的角不同时,可以分别得到圆、椭圆、双曲线和抛物线.能通过章引言初步认识本章的学习内容、学习方法与学习价值.
2.能通过绘制椭圆的过程认识椭圆的几何特征,给出椭圆的定义,并能用它解决简单的问题,发展数学抽象素养.
3.能建立适当的坐标系得到椭圆的标准方程,并能用它解决简单的问题.体会建立曲线的方程的方法,发展直观想象、数学运算素养.
2 新知建构
问题3:取一条定长的细绳,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点F1,F2,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线 在这一过程中,移动的笔尖(动点)满足的几何条件是什么
问题4:你能用精确的数学语言刻画椭圆吗
我们把平面内与两个定点F1,F2的距离的和等于常数(大于| F1F2 |)的点的轨迹叫做椭圆(ellipse).
这两个定点叫做椭圆的焦点(focus),两焦点间的距离叫做椭圆的焦距(focus distance),焦距的一半称为半焦距.
椭圆的定义
当常数等于两定点间的距离时,点的轨迹是线段;
当常数小于两定点间的距离时,点的轨迹不存在.
问题5:遵循解析几何研究几何图形的内在逻辑,了解椭圆的概念后,应建立椭圆的方程.你能猜想建立椭圆方程的大致步骤吗 请尝试建立椭圆的方程.
以经过椭圆两焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系xOy.
M(x,y)
F1
F2
x
y
(c,0)
P={M|MF1+MF2=2a}
P
F1
F2
x
y
O
问题6:如果椭圆的焦点F1,F2在y轴上,且F1,F2的坐标分别为(0,-c),(0,c),a,b的意义同上,那么椭圆的方程又是什么
y
O
x
F1
F2
M
此时椭圆的方程为
这也是椭圆的标准方程.
椭圆的方程
根据椭圆的几何特征建立适当的直角坐标系
明确椭圆上的点满足的几何条件
将几何条件转化为代数表示列出方程
化简方程
检验方程
M
F1
F2
x
y
y
O
x
F1
F2
M
3 数学运用
3 数学运用
4 回顾反思
问题7:
(1)椭圆的概念中的要点与需要注意的地方分别是什么
(2)推导椭圆的标准方程时,建立直角坐标系的依据是什么
(3)椭圆标准方程的推导给了你怎样的启示 就一般情况而言,求曲线的方程有哪些步骤 为什么是这些步骤
5 学习评价
1.尝试通过其他化简方案推导椭圆的标准方程.
2.完成教科书习题3.1第1,2题.
实践:请利用细绳、铅笔,动手操作,画一个椭圆.
再 见
汇报人姓名
