6.4 生活中的圆周运动 课件(共27张PPT)
文档属性
| 名称 | 6.4 生活中的圆周运动 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 34.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-15 18:55:22 | ||
图片预览








文档简介
(共27张PPT)
生活中的圆周运动
F
“供需"平衡 物体做匀速圆周运动
受力分析:
提供物体做匀速圆周运动的力
做匀速圆周运动所需求的向心力
匀速圆周运动解题思路
从“供”“需"两方面研究做圆周运动的物体
T
G
F
实例研究1——火车转弯
2013年西班牙列车脱轨事故
火车转弯多少速度是合理的呢?
“本来速度应该是80km/h,我开到了190km/h”
火车转弯限速
来源:《新闻直播间》https://tv./
火车车轮的构造
突出的轮缘
实例研究1——火车转弯
N
FN
G
外轨对轮缘的弹力
内轨
外轨
① 水平弯道(内外轨道一样高)
缺点:由于火车质量很大,故轮缘和外轨间的弹力很大,铁轨容易损坏、变形,火车侧翻。
“供需”平衡
实例研究1——火车转弯
真实铁路转弯处:
外轨高于内轨
实例研究1——火车转弯
实验模拟:“弹珠飞车”模型
实例研究1——火车转弯
向心力恰好由重力G和支持力FN的合力提供
FN
② 外轨略高于内轨(倾斜轨道)
θ
“完美”的过弯
实例研究1——火车转弯
所需向心力
Fn=F
“供需”平衡
提供的力
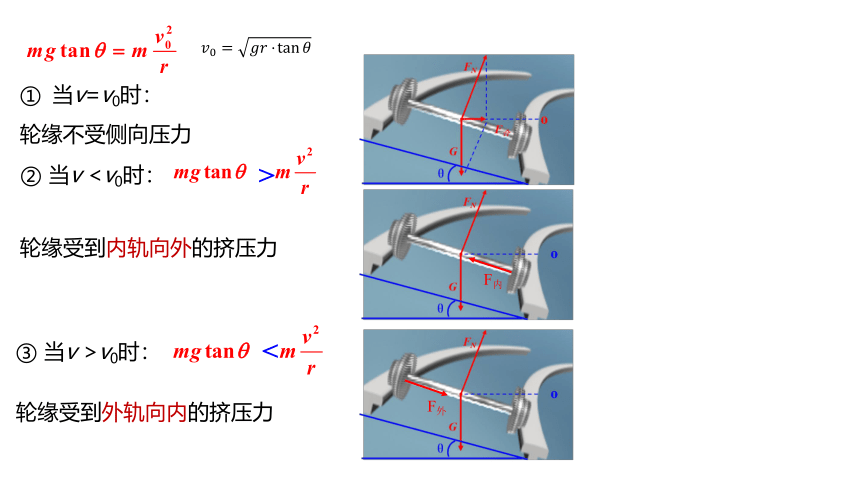
当v=v0时:
② 当v轮缘不受侧向压力
轮缘受到内轨向外的挤压力
F内
>
③ 当v >v0时:
轮缘受到外轨向内的挤压力
<
F外
θ
思考:汽车在水平路面上转弯时,向心力由什么力提供呢?
思考:如果汽车的速度过大,会出现什么情况呢?有什么解决方法?
解决方法:
把转弯处的道路修成外高内低。
(再次供需平衡)
FN
F
G
G
f
FN
Fn=f =
“供需”不平衡,所需向心力很大,摩擦力提供不足。
高速转弯处
自行车赛道
思考:高速过弯道需要改变轨道。你是否能找到第二种方法,不改变轨道的前提下使火车既能提速过弯道又保证安全?
摆式列车在转弯时可以侧向摆动,可在弯曲路段高速驶过,无需减速。
实例研究2——汽车过桥
如果坐车驶过以下路段,你会有什么样的感受?
FN ’>mg
凹形桥
由牛顿第三定律得
超重
“供需”平衡
G
FN
拱形桥
由牛顿第三定律得
失重
FN ’<mg
R
O
R
O
v
G
FN
模型总结:汽车过两类桥最低点/最高点对桥的压力
模型总结:汽车过两类桥最低点/最高点对桥的压力
由牛顿第三定律得
G
FN
拱形桥
R
O
v
当FN'= 0 时,重力作为向心力.汽车接下来将做初速度水平,只受重力的平抛运动
v2
R
mg=m
v↑ FN'↓
思考:在拱形桥上速度可以无限大吗?如果有最大速度,最大是多少
如果把地球看成一个巨大的拱桥,速度大到一定程度时,会发生什么?
当FN'= 0 时,仅有重力作向心力.地面对车的支持力为0
v2
R
mg=m
v2
R
FN =mg-m
【情景研究】宇宙飞船绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg ,求此时座舱对航天员的支持力是多少?
v2
R
mg-FN= m
当 时,座舱对航天员的支持力FN=0
——航天员处于完全失重
mg
FN
实例研究3——航天器中的失重现象
实例研究3——航天器中的失重现象
失重并不是因为离地球太远,摆脱了地球引力。相反正由于地球引力存在,才使得航天员可能做环绕地球的圆周运动。
思考:完全失重是不是摆脱了地球引力?
v2
R
mg=m
供需不平衡会怎样?
FN
G
FN
v
G
FN
v
实例研究1——火车转弯
实例研究2——汽车过桥
实例研究3——航天器中的失重现象
mg
FN
做圆周运动的物体,由于惯性,总有沿着切线方向飞出去的倾向。
A
o
模型讨论:绳拴小球在水平面上做匀速圆周运动时,小球所需向心力由形变的绳产生的弹力提供。若m、r、ω一定,向心力F=mω2r
思考1:若突然松手,小球将怎样运动?
思考2:若绳的拉力F小于它做圆周运动所需的向心力,小球将怎样运动
沿着切线飞出
虽然不会沿着切线飞去,也会逐渐远离圆心
A
o
4.离心运动
做圆周运动的物体,在所受合外力突然消失或不足以提供圆周运动所需向心力时,就做逐渐远离圆心的运动,这种运动就叫离心运动。
供需关系 运动情况
F供=F需向
F供=0
F供F供>F需向
圆周运动
切线方向
离心运动
近心运动
离心抛掷
离心脱水
离心分离
离心甩干
离心运动的应用
离心运动的防止
高速转动的砂轮不能超过允许的最大转速,否则内部分子间相互作用力不足以提供所需向心力,离心运动使它们破裂
水平公路上行驶的汽车,如果转弯速度过大,所需向心力很大,大于最大静摩擦力,汽车将做离心运动而造成事故。所以汽车在弯道时不能超过规定的车速。
例题:如图所示是摩托车比赛转弯时的情形,转弯处路面常是外高内低,摩托车转弯有一个最大安全速度,若超过此速度,摩托车将发生滑动.对于摩托车滑动的问题,下列论述正确的是( )
A.摩托车一直受到沿半径方向向内的向心力作用
B.摩托车所受外力的合力小于所需的向心力
C.摩托车将沿其线速度的方向沿直线滑去
D.摩托车将沿其半径方向沿直线滑去
B
课堂小结
G
FN
v
G
FN
v
实例研究1——火车转弯
实例研究2——汽车过桥
“供需"平衡
实例研究3——航天器中的失重现象
离心运动
A
o
离心运动的应用
离心运动的防止
“供需"不平衡
作业
完成课后练习
完成课本“练习与应用”
生活中的圆周运动
F
“供需"平衡 物体做匀速圆周运动
受力分析:
提供物体做匀速圆周运动的力
做匀速圆周运动所需求的向心力
匀速圆周运动解题思路
从“供”“需"两方面研究做圆周运动的物体
T
G
F
实例研究1——火车转弯
2013年西班牙列车脱轨事故
火车转弯多少速度是合理的呢?
“本来速度应该是80km/h,我开到了190km/h”
火车转弯限速
来源:《新闻直播间》https://tv./
火车车轮的构造
突出的轮缘
实例研究1——火车转弯
N
FN
G
外轨对轮缘的弹力
内轨
外轨
① 水平弯道(内外轨道一样高)
缺点:由于火车质量很大,故轮缘和外轨间的弹力很大,铁轨容易损坏、变形,火车侧翻。
“供需”平衡
实例研究1——火车转弯
真实铁路转弯处:
外轨高于内轨
实例研究1——火车转弯
实验模拟:“弹珠飞车”模型
实例研究1——火车转弯
向心力恰好由重力G和支持力FN的合力提供
FN
② 外轨略高于内轨(倾斜轨道)
θ
“完美”的过弯
实例研究1——火车转弯
所需向心力
Fn=F
“供需”平衡
提供的力
当v=v0时:
② 当v
轮缘受到内轨向外的挤压力
F内
>
③ 当v >v0时:
轮缘受到外轨向内的挤压力
<
F外
θ
思考:汽车在水平路面上转弯时,向心力由什么力提供呢?
思考:如果汽车的速度过大,会出现什么情况呢?有什么解决方法?
解决方法:
把转弯处的道路修成外高内低。
(再次供需平衡)
FN
F
G
G
f
FN
Fn=f =
“供需”不平衡,所需向心力很大,摩擦力提供不足。
高速转弯处
自行车赛道
思考:高速过弯道需要改变轨道。你是否能找到第二种方法,不改变轨道的前提下使火车既能提速过弯道又保证安全?
摆式列车在转弯时可以侧向摆动,可在弯曲路段高速驶过,无需减速。
实例研究2——汽车过桥
如果坐车驶过以下路段,你会有什么样的感受?
FN ’>mg
凹形桥
由牛顿第三定律得
超重
“供需”平衡
G
FN
拱形桥
由牛顿第三定律得
失重
FN ’<mg
R
O
R
O
v
G
FN
模型总结:汽车过两类桥最低点/最高点对桥的压力
模型总结:汽车过两类桥最低点/最高点对桥的压力
由牛顿第三定律得
G
FN
拱形桥
R
O
v
当FN'= 0 时,重力作为向心力.汽车接下来将做初速度水平,只受重力的平抛运动
v2
R
mg=m
v↑ FN'↓
思考:在拱形桥上速度可以无限大吗?如果有最大速度,最大是多少
如果把地球看成一个巨大的拱桥,速度大到一定程度时,会发生什么?
当FN'= 0 时,仅有重力作向心力.地面对车的支持力为0
v2
R
mg=m
v2
R
FN =mg-m
【情景研究】宇宙飞船绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg ,求此时座舱对航天员的支持力是多少?
v2
R
mg-FN= m
当 时,座舱对航天员的支持力FN=0
——航天员处于完全失重
mg
FN
实例研究3——航天器中的失重现象
实例研究3——航天器中的失重现象
失重并不是因为离地球太远,摆脱了地球引力。相反正由于地球引力存在,才使得航天员可能做环绕地球的圆周运动。
思考:完全失重是不是摆脱了地球引力?
v2
R
mg=m
供需不平衡会怎样?
FN
G
FN
v
G
FN
v
实例研究1——火车转弯
实例研究2——汽车过桥
实例研究3——航天器中的失重现象
mg
FN
做圆周运动的物体,由于惯性,总有沿着切线方向飞出去的倾向。
A
o
模型讨论:绳拴小球在水平面上做匀速圆周运动时,小球所需向心力由形变的绳产生的弹力提供。若m、r、ω一定,向心力F=mω2r
思考1:若突然松手,小球将怎样运动?
思考2:若绳的拉力F小于它做圆周运动所需的向心力,小球将怎样运动
沿着切线飞出
虽然不会沿着切线飞去,也会逐渐远离圆心
A
o
4.离心运动
做圆周运动的物体,在所受合外力突然消失或不足以提供圆周运动所需向心力时,就做逐渐远离圆心的运动,这种运动就叫离心运动。
供需关系 运动情况
F供=F需向
F供=0
F供
圆周运动
切线方向
离心运动
近心运动
离心抛掷
离心脱水
离心分离
离心甩干
离心运动的应用
离心运动的防止
高速转动的砂轮不能超过允许的最大转速,否则内部分子间相互作用力不足以提供所需向心力,离心运动使它们破裂
水平公路上行驶的汽车,如果转弯速度过大,所需向心力很大,大于最大静摩擦力,汽车将做离心运动而造成事故。所以汽车在弯道时不能超过规定的车速。
例题:如图所示是摩托车比赛转弯时的情形,转弯处路面常是外高内低,摩托车转弯有一个最大安全速度,若超过此速度,摩托车将发生滑动.对于摩托车滑动的问题,下列论述正确的是( )
A.摩托车一直受到沿半径方向向内的向心力作用
B.摩托车所受外力的合力小于所需的向心力
C.摩托车将沿其线速度的方向沿直线滑去
D.摩托车将沿其半径方向沿直线滑去
B
课堂小结
G
FN
v
G
FN
v
实例研究1——火车转弯
实例研究2——汽车过桥
“供需"平衡
实例研究3——航天器中的失重现象
离心运动
A
o
离心运动的应用
离心运动的防止
“供需"不平衡
作业
完成课后练习
完成课本“练习与应用”
