贵州省贵阳市清华中学、安顺一中等校2023-2024学年高一下学期第一次联考数学试题(含答案)
文档属性
| 名称 | 贵州省贵阳市清华中学、安顺一中等校2023-2024学年高一下学期第一次联考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 716.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 07:24:22 | ||
图片预览



文档简介
2026届高一年级第一次联考试题
数学学科
考试时间:120分钟:总分:150分
注意事项:
1.答题前填写好自己的姓名 班级 考号等信息。
2.请将答案正确填写在答题卡上。
一 选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,则下列表述正确的是( )
A. B. C. D.
2.已知向量,则( )
A.2 B.3 C. D.
3.已知复数,则复数Z的共轭复数=( )
A. B. C. D.
4.已知,则的最大值是( )
A. B.3 C.1 D.6
5. 已知锐角的终边过点(2,1),则 ( )
A. B. C. D.
6.已知向量,,若,则( )
A. B. C. D.
7.若函数是定义在上的偶函数,则
A.34 B.25 C.16 D.9
8.已知的内角A,B,C的对边分别为,若,且,则 ( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列结论中,错误的是( )
A.表示两个相等向量的有向线段,若它们的起点相同,则终点也相同;
B.若,则,不是共线向量;
C.若,则四边形是平行四边形;
D.与同向,且,则
10.以下运算中正确的有( )
A.若,则
B.
C.
D.
11.下列命题为真命题的是( )
A.复数在复平面内对应的点在第二象限
B.若为虚数单位,为正整数,则
C.若复数为纯虚数,则,
D.若,, ,则在复平面内对应的点形成的图形的面积为.
三 填空题:本题共3小题,每小题5分,共15分.
12.已知向量,的夹角为,,,则= .
13.一个扇形的弧长为,面积为,则此扇形的圆心角为 .(用弧度制表示)
14.在2022年2月4日举行的北京冬奥会开幕式上,贯穿全场的雪花元素为观众带来了一场视觉盛宴,象征各国 各地区代表团的91朵“小雪花”汇聚成一朵代表全人类“一起走向未来”的“大雪花”的意境惊艳了全世界,顺次连接图中各顶点可近似得到正六边ABCDEF.已知正六边形的边长为1,点P是其内部一点(包含边界),则的最大值是
第16题图
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
已知,存在满足。
求向量、、的坐标; (2)求与夹角的余弦值.
(15分)
在中,内角所对的边分别是,已知.
(1)求角;
(2)若,求周长的最大值。
17.(15分)
1707年4月15日,欧拉出生在瑞士巴塞尔一个牧师家庭,自幼受父亲的熏陶,喜爱数学。13岁入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。是十八世纪数学界最杰出的人物之一,数学史上称十八世纪为“欧拉时代”.1735年,他提出公式:复数:(是虚数单位).已知复数,,.
(1)当时,求的值; (2)当时,若且求的值.
18.(17分)
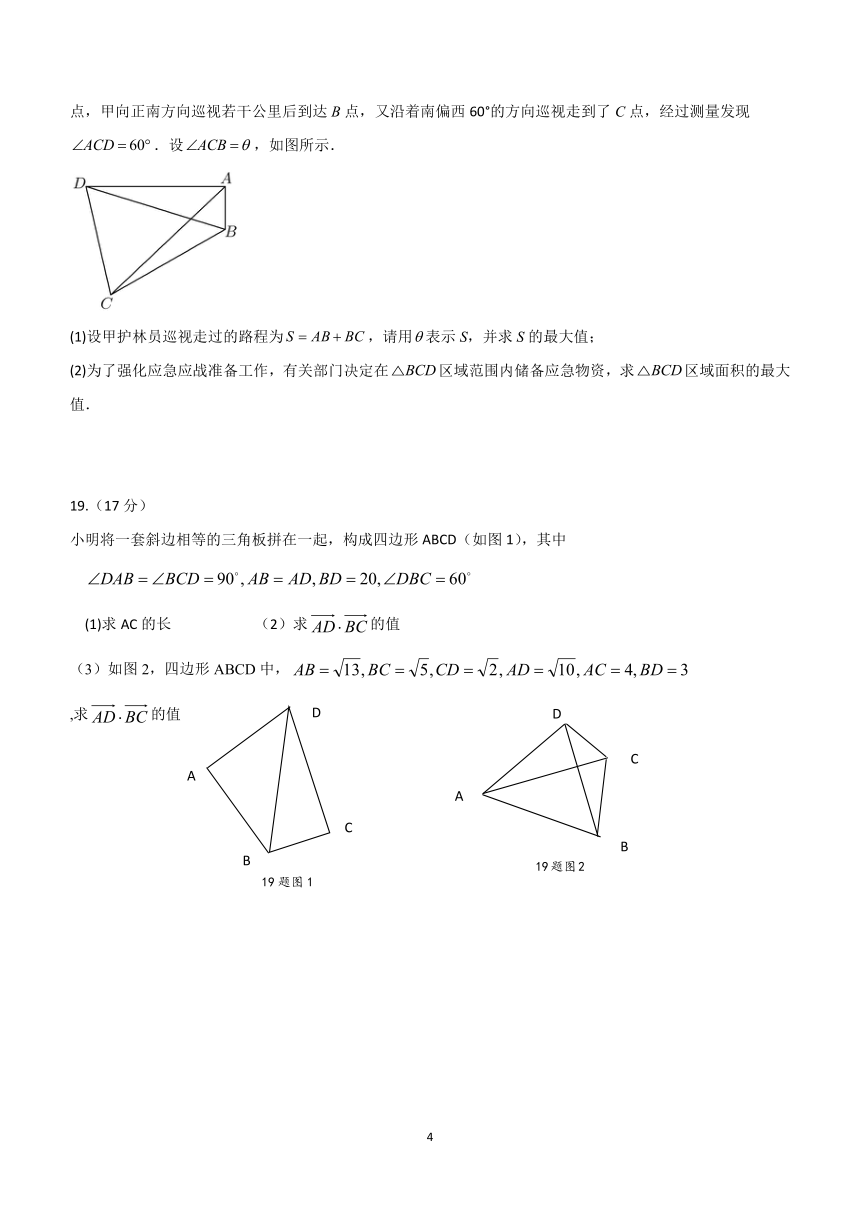
今年2月,贵州省多地连续高温,森林防灭火形势严峻,某县消防部门安排了甲、乙两名森林防火护林员对该县一区域开展巡查.现甲、乙两名森林防火护林员同时从A地出发,乙沿着正西方向巡视走了3km后到达D点,甲向正南方向巡视若干公里后到达B点,又沿着南偏西60°的方向巡视走到了C点,经过测量发现.设,如图所示.
(1)设甲护林员巡视走过的路程为,请用表示S,并求S的最大值;
(2)为了强化应急应战准备工作,有关部门决定在区域范围内储备应急物资,求区域面积的最大值.
19.(17分)
小明将一套斜边相等的三角板拼在一起,构成四边形ABCD(如图1),其中
(1)求AC的长 (2)求的值
(3)如图2,四边形ABCD中,
,求的值
2026届高一年级第一次联考试题答案
选择题(单选) :
1 2 3 4 5 6 7 8
C A D B B C A B
选择题(多选):
9 10 11
BCD AC CD
9.【详解】对于A,表示两个相等向量的有向线段,若它们的起点相同,则终点也相同,故A正确;
对于B,若也有可能,长度不等,但方向相同或相反,即共线,故B错误;
对于C,若,则,可以方向不同,所以四边形不一定是平行四边形,故C错误;
对于D,因为向量是既有大小又有方向的量,所以任何两个向量都不能比较大小,故D错误.
故选:BCD.
10.【详解】对于A:,故A正确;
对于B:
,故B错误;
对于C:,故C正确;
对于D:,故D错误, 故选:AC.
11.【详解】对于A,复数在复平面内对应的点为,在第四象限,故A错误;
对于B,,故B错误;
对于C,复数为纯虚数,则,故C正确;
对于D,在复平面内表示到点距离小于等于1的所有的点,所以形成的图形为以为圆心1为半径的圆,所以面积为,故D正确; 故选:CD.
填空题
13. 14.3
14、【详解】 作
要使最大,必须让
所以
如图可知,当在处时,最大,从而最大
此时 故答案为:3
四、解答题:
15、【详解】(1),且
......2分
,......6分
设与夹角为,,......8分
,......11分
.......13分
【详解】(1)在中,由正弦定理可知原式 可化为 ,化简得,,......4分
在中,由余弦定理得,,......7分
又因为,所以......9分
(2)由余弦定理得
当且仅当时取等号,所以周长的最大值为;......15分
【详解】(1)因为虚数不能比较大小,所以为实数,......2分
又因为,所以 ......6分 解得......8分
(2)当时,,,......10分
所以,
18.【详解】(1)由题意知:.......1分
在中,由正弦定理:,即:,......2分
在中,∵,∴.
由正弦定理:,......5分
,,......6分
∴且,又,......7分
∵,∴,
∴S的最大值为,当且仅当时取得等号.......9分
(2)由(1)知:,.
∴......11分
,
∴,......14分
不妨设,又∵,∴,,
∴而S在上单调递增,
,当且仅当时取得等号.......17分
解:(1) 由题知
由余弦定理得:
延长DA,CB交于E,易知
两式相减得:
D
D
B
19题图1
C
A
19题图2
A
B
C
数学学科
考试时间:120分钟:总分:150分
注意事项:
1.答题前填写好自己的姓名 班级 考号等信息。
2.请将答案正确填写在答题卡上。
一 选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合,则下列表述正确的是( )
A. B. C. D.
2.已知向量,则( )
A.2 B.3 C. D.
3.已知复数,则复数Z的共轭复数=( )
A. B. C. D.
4.已知,则的最大值是( )
A. B.3 C.1 D.6
5. 已知锐角的终边过点(2,1),则 ( )
A. B. C. D.
6.已知向量,,若,则( )
A. B. C. D.
7.若函数是定义在上的偶函数,则
A.34 B.25 C.16 D.9
8.已知的内角A,B,C的对边分别为,若,且,则 ( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.下列结论中,错误的是( )
A.表示两个相等向量的有向线段,若它们的起点相同,则终点也相同;
B.若,则,不是共线向量;
C.若,则四边形是平行四边形;
D.与同向,且,则
10.以下运算中正确的有( )
A.若,则
B.
C.
D.
11.下列命题为真命题的是( )
A.复数在复平面内对应的点在第二象限
B.若为虚数单位,为正整数,则
C.若复数为纯虚数,则,
D.若,, ,则在复平面内对应的点形成的图形的面积为.
三 填空题:本题共3小题,每小题5分,共15分.
12.已知向量,的夹角为,,,则= .
13.一个扇形的弧长为,面积为,则此扇形的圆心角为 .(用弧度制表示)
14.在2022年2月4日举行的北京冬奥会开幕式上,贯穿全场的雪花元素为观众带来了一场视觉盛宴,象征各国 各地区代表团的91朵“小雪花”汇聚成一朵代表全人类“一起走向未来”的“大雪花”的意境惊艳了全世界,顺次连接图中各顶点可近似得到正六边ABCDEF.已知正六边形的边长为1,点P是其内部一点(包含边界),则的最大值是
第16题图
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
已知,存在满足。
求向量、、的坐标; (2)求与夹角的余弦值.
(15分)
在中,内角所对的边分别是,已知.
(1)求角;
(2)若,求周长的最大值。
17.(15分)
1707年4月15日,欧拉出生在瑞士巴塞尔一个牧师家庭,自幼受父亲的熏陶,喜爱数学。13岁入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。是十八世纪数学界最杰出的人物之一,数学史上称十八世纪为“欧拉时代”.1735年,他提出公式:复数:(是虚数单位).已知复数,,.
(1)当时,求的值; (2)当时,若且求的值.
18.(17分)
今年2月,贵州省多地连续高温,森林防灭火形势严峻,某县消防部门安排了甲、乙两名森林防火护林员对该县一区域开展巡查.现甲、乙两名森林防火护林员同时从A地出发,乙沿着正西方向巡视走了3km后到达D点,甲向正南方向巡视若干公里后到达B点,又沿着南偏西60°的方向巡视走到了C点,经过测量发现.设,如图所示.
(1)设甲护林员巡视走过的路程为,请用表示S,并求S的最大值;
(2)为了强化应急应战准备工作,有关部门决定在区域范围内储备应急物资,求区域面积的最大值.
19.(17分)
小明将一套斜边相等的三角板拼在一起,构成四边形ABCD(如图1),其中
(1)求AC的长 (2)求的值
(3)如图2,四边形ABCD中,
,求的值
2026届高一年级第一次联考试题答案
选择题(单选) :
1 2 3 4 5 6 7 8
C A D B B C A B
选择题(多选):
9 10 11
BCD AC CD
9.【详解】对于A,表示两个相等向量的有向线段,若它们的起点相同,则终点也相同,故A正确;
对于B,若也有可能,长度不等,但方向相同或相反,即共线,故B错误;
对于C,若,则,可以方向不同,所以四边形不一定是平行四边形,故C错误;
对于D,因为向量是既有大小又有方向的量,所以任何两个向量都不能比较大小,故D错误.
故选:BCD.
10.【详解】对于A:,故A正确;
对于B:
,故B错误;
对于C:,故C正确;
对于D:,故D错误, 故选:AC.
11.【详解】对于A,复数在复平面内对应的点为,在第四象限,故A错误;
对于B,,故B错误;
对于C,复数为纯虚数,则,故C正确;
对于D,在复平面内表示到点距离小于等于1的所有的点,所以形成的图形为以为圆心1为半径的圆,所以面积为,故D正确; 故选:CD.
填空题
13. 14.3
14、【详解】 作
要使最大,必须让
所以
如图可知,当在处时,最大,从而最大
此时 故答案为:3
四、解答题:
15、【详解】(1),且
......2分
,......6分
设与夹角为,,......8分
,......11分
.......13分
【详解】(1)在中,由正弦定理可知原式 可化为 ,化简得,,......4分
在中,由余弦定理得,,......7分
又因为,所以......9分
(2)由余弦定理得
当且仅当时取等号,所以周长的最大值为;......15分
【详解】(1)因为虚数不能比较大小,所以为实数,......2分
又因为,所以 ......6分 解得......8分
(2)当时,,,......10分
所以,
18.【详解】(1)由题意知:.......1分
在中,由正弦定理:,即:,......2分
在中,∵,∴.
由正弦定理:,......5分
,,......6分
∴且,又,......7分
∵,∴,
∴S的最大值为,当且仅当时取得等号.......9分
(2)由(1)知:,.
∴......11分
,
∴,......14分
不妨设,又∵,∴,,
∴而S在上单调递增,
,当且仅当时取得等号.......17分
解:(1) 由题知
由余弦定理得:
延长DA,CB交于E,易知
两式相减得:
D
D
B
19题图1
C
A
19题图2
A
B
C
同课章节目录
