2024河南考数学二轮中考题型研究 题型四 类比、拓展探究题题(课件)(共30张PPT)
文档属性
| 名称 | 2024河南考数学二轮中考题型研究 题型四 类比、拓展探究题题(课件)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 791.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 11:53:48 | ||
图片预览






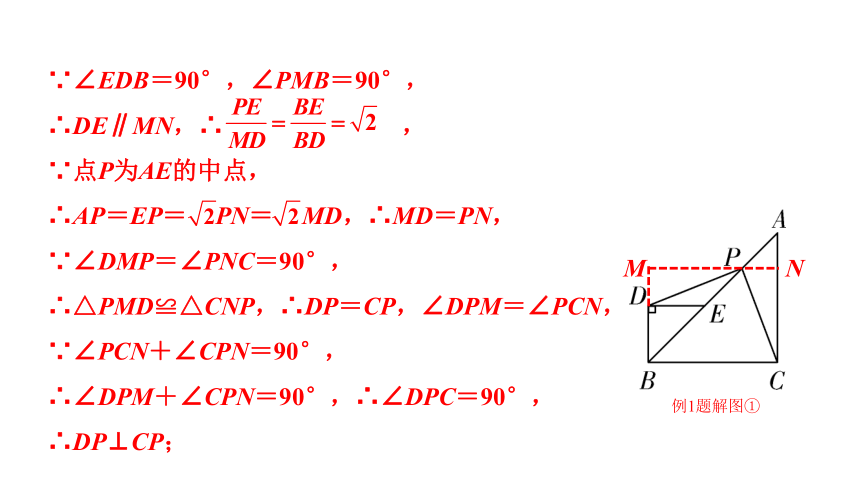




文档简介
(共30张PPT)
题型四 类比、拓展探究题
(10年8考)
【题型解读】近10年考查8次,其考查类型和频次为:①与图形旋转有关的探究考查6次;②与动点有关的探究考查2次.
类型一 与图形旋转有关的探究
典例精讲
例1 (1)观察猜想
如图①,在Rt△ABC中,∠ACB=90°,AC=BC, 在Rt△BDE中,∠BDE=90°,BD=DE,连接AE,取AE边的中点P,连接DP、CP.
例1题图①
填空:①DP与CP的数量关系是________;
②DP与CP的位置关系是____________;
【思维教练】①要求DP与CP的数量关系,通过直角三角形的性质:斜边上的中线等于斜边的一半,即可得到CP= AE,DP= AE,即可求解;②要求DP与CP的位置关系,
即求∠DPC的度数,通过等腰三角形性质
和三角形的内外角关系,得到∠DPC=2∠BAC,
通过题干得到∠BAC的度数,即可求解.
例1题图①
【解法提示】
∵∠ACB=90°,点P为AE的中点,∴PC为Rt△AEC斜边AE的中线,∴CP= AE,同理可证,DP= AE,∴DP=CP;
∴∠DPE=2∠DAE,∠CPE=2∠CAE,
∵AC=BC,∴∠BAC=45°,∴∠DPC=2∠BAC=90°,∴DP⊥CP.
填空:①DP与CP的数量关系是________;
②DP与CP的位置关系是________;
DP=CP
DP⊥CP
例1题图①
(2)类比探究
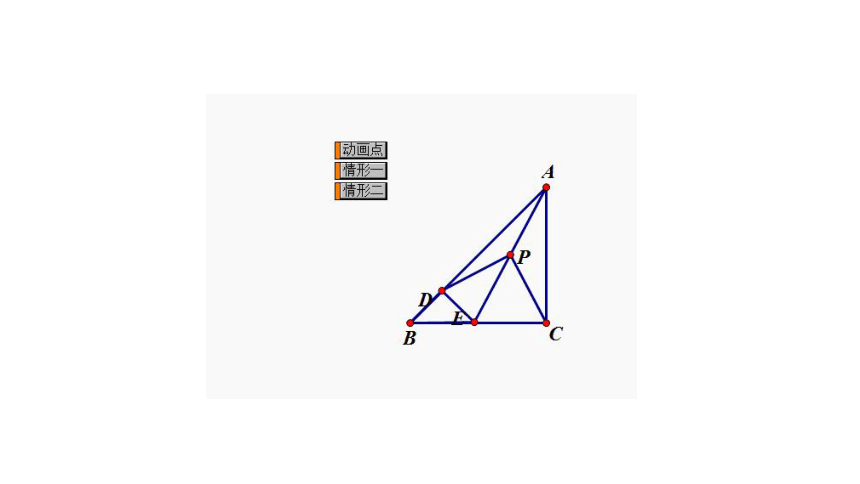
把△BDE绕点B逆时针旋转45°至如图②的位置,(1)中的结论是否仍然成立?若成立,请就图②的情形给出证明;若不成立,请说明理由;
例1题图②
【思维教练】要求DP与CP的数量关系和位置关系,过点P作AC的垂线,并构造出DP与PC所在的两个直角三角形,结合旋转的性质可证明DP和PC所在的两个三角形全等,即可求解.
(1)中的结论仍然成立.
证明:如解图①,过点P作MN⊥AC于点N,交BD的延长线于点M,
易得四边形BCNM为矩形,
∴CN=BM.
∵等腰Rt△BDE绕点B逆时针旋转45°,
∴∠MBA=45°,
∴MP=BM,
∴MP=CN,
例1题解图①
N
M
∵∠EDB=90°,∠PMB=90°,
∴DE∥MN,∴ ,
∵点P为AE的中点,
∴AP=EP= PN= MD,∴MD=PN,
∵∠DMP=∠PNC=90°,
∴△PMD≌△CNP,∴DP=CP,∠DPM=∠PCN,
∵∠PCN+∠CPN=90°,
∴∠DPM+∠CPN=90°,∴∠DPC=90°,
∴DP⊥CP;
例1题解图①
N
M
(3)问题解决
若BC=3BD=3 ,将图①中△BDE绕点B在平面内自由旋转,当BE⊥AB时,直接写出线段CP的长.
例1题图①
【思维教练】分△BDE在BC的上方和下方两种情况讨论,利用(2)中的结论可得△PCD为等腰直角三角形,结合题意即可求解.
【解法提示】分两种情况讨论:①如解图②,
由(2)可知DP⊥CP,DP=CP,∴△PCD为等腰直角三角形,
∵BC=3BD=3 ,∴CD=BD+BC=4 ,∴PC=4;
例1题解图②
例1题解图③
②如解图③,由(2)可知DP⊥CP,DP=CP,
∴△PCD为等腰直角三角形,
∵BC=3BD=3 ,∴CD=BC-BD=2 ,∴CP=2.
综上所述,CP的长为4或2.
(3)CP的长为4或2.
类型二 与动点有关的探究
典例精讲
例1 如图,在正方形ABCD中,点E,F分别在射线CD,BC 上,且BF=CE,过点C作CG⊥EF,垂足为点G,CG交射线DB于点H.
(1)如图①,当点E是线段CD的中点,点 F在线段BC上时,线段CH与EF之间的数量关系为____________;
例1题图①
【思维教练】要求CH与EF之间的数量关系,观察图象可知,故考虑CH,EF与BD之间的数量关系,利用三角形中位线的性质即可求出EF= BD,再利用直角三角形中线的性质可求出CH= BD,等量代换即可求出线段CH与EF之间的数量关系.
例1题图①
【解法提示】∵点E是线段CD的中点,∴CE=ED.
∵BC=CD,BF=CE,∴BF=CF,
∴EF∥BD,EF= BD.
∵CG⊥EF,∴CH⊥BD.
∵四边形ABCD是正方形,∴CH= BD,∴CH=EF.
(1)如图①,当点E是线段CD的中点,点 F在线段BC上时,线段CH与EF之间的数量关系为________;
例1题图①
CH=EF
(2)如图②,当点E,F分别在线段CD,BC的延长线上时,判断(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
例1题图②
例1题图②
【思维教练】在CE上截取CM=CF,通过构造△HBC≌△FME,利用全等三角形的性质即可证得CH=EF.
证明:如解图①,在CE上截取CM=CF,连接MF,
(2)成立
M
∵BF=CE,∴BF-CF=CE-CM,∴BC=EM.
∵∠FCM=90°,FC=MC,
∴∠CMF=45°,∴∠FME=135°.
∵∠DBC=45°,
∴∠HBC=135°,∴∠HBC=∠FME.
∵CG⊥EF,
∴∠CGE=90°,
∴∠CEG+∠ECG=90°.
∵∠HCB+∠BCD+∠ECG=180°,∠BCD=90°,
∴∠HCB+∠ECG=90°,
∴∠HCB=∠GEC,
∴△HBC≌△FME(ASA),
∴CH=EF;
例1题图②
M
(3)已知正方形ABCD的边长为6,BH=2 ,请直接写出线段EF的长.
备用图
【思维教练】分点H在对角线BD上和点H在DB的延长线上两种情况进行讨论.
例题解图②
例题解图③
【解法提示】如解图②和解图③,连接AC交BD于点O,则OB=OC=3 ,
∵OH=OB-BH,
∴OH=3 -2 = .
在△OHC中,∠COH=90°,
由勾股定理得CH= .
∵四边形ABCD是正方形,
∴BC=CD,∴∠HBC=45°.
分两种情况讨论:
①如解图②,当点H在对角线BD上时, 延长DC至点M,使CM=CF,连接FM.
例题解图②
∵CF=CM,∴∠FME=45°.
∵CG⊥EF,
∴∠CFE+∠HCF=90°,
又∵∠CEF+∠CFE=90°,
∴∠CEF=∠HCB.
∵BF=CE,CF=CM,∴BC=EM,
∴△BHC≌△MFE,
∴EF=CH=2 ;
例题解图②
②如解图③,当点H在线段DB的延长线上时,
例题解图③
∵OH=OB+BH,
∴OH=3 +2 =5 .
在△OHC中,∠COH=90°,
由勾股定理得CH= ,
由(2)得EF=CH,
∴EF=CH=2 .
综上所述,EF的长为2 或2 .
类型三 与折叠、平移有关的探究
典例精讲
例1 在矩形ABCD中,BC= CD,点E、F分别是边AD、BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
例1题图①
【思维教练】由折叠的性质可得∠PEF=∠FED,由矩形的性质可得AD∥BC,进而得到∠FED=∠EFP,通过等量代换可得∠PEF=∠EFP,进而通过等角对等边即可求证PE=PF.
(1)证明:根据折叠性质,∠PEF=∠FED,
∵AD∥BC,
∴∠FED=∠EFP,
∴∠PEF=∠EFP,
∴PE=PF;
例1题图①
(2)如图②,当点P在线段CB的延长线上时,GH交AB于点M,求证:点M在线段EF的垂直平分线上;
例1题图②
【思维教练】由矩形的性质及折叠的性质,结合题目条件可得EH=BF,由(1)进而可得PH=PB,再通过构造Rt△MHE≌Rt△MBF可得ME=MF,进而可证点M在线段EF的垂直平分线上.
∵AD=BC,AE=CF,
∴ED=BF,∴EH=BF,
又∵由(1)知PE=PF,
∴PH=PB,
∵∠PHM=∠PBM=90°,PM是公共边,
∴Rt△PHM≌Rt△PBM,∴HM=BM,
∴Rt△MHE≌Rt△MBF,∴ME=MF,
∴点M在线段EF的垂直平分线上;
(2)证明:如解图①,连接PM、EM、FM,
例1题解图①
(3)当AB=5时,在点E由点A移动到AD中点的过程中,计算出点G运动的路线长.
备用图
【思维教练】通过观察可知,点E从点A移动到AD中点的过程中,点G运动的路线是以矩形中心到点C的距离为半径的圆周长的 ,进而通过弧长公式即可求出点G运动的路线长.
(3)解:如解图②,连接AC,BD,交点为O,连接OG,点E从点A移动到AD中点的过程中,点G运动路径是 ,
在Rt△BCD中,∵BC= CD,
∴tan∠CBD= ,
∴∠CBD=30°,∠ABO=60°,
∴△AOB是等边三角形,
∴OB=OC=AB=5,∠BOC=120°,
∴点G运动的路线长= = .
例1题解图②
例2 综合与探究
问题情境
在数学活动课上,老师让同学们准备两张全等的直角三角形纸片,Rt△ABC≌Rt△DEF,AC=DF=6 cm,BC=EF=8 cm,∠ACB=∠DFE=90°.
实践操作
(1)如图①,把Rt△ABC和Rt△DEF的直角边
BC和EF部分重合,使点E,C,F,B在同一
条直线上,连接AE和BD,得到四边形AEDB.
请说明四边形AEDB的形状并证明;
例2题图①
【思维教练】根据Rt△ABC≌Rt△DEF可得AB=ED,∠ABC=∠BED,进而可得AB∥DE,即可得到四边形AEDB的形状.
(1)解:四边形AEDB是平行四边形.
证明:∵Rt△ABC≌Rt△DEF,
∴AB=ED,∠ABC=∠BED.
∴AB∥ED.
∴四边形AEDB是平行四边形;
例2题图①
实践探究
(2)勤奋小组的同学在图①的基础上,将△DEF沿射线BC平移,其中△ABC不动,得到的四边形AEDB是矩形,如图②,请求出此时BE的长;
例2题图②
【思维教练】根据已知条件,在Rt△ABC中可求出AB的长,进而在Rt△ABE和Rt△ECA中,由勾股定理即可求解.
(2)∵四边形AEDB是矩形,∴∠EAB=90°.
∵AC=6 cm,BC=8 cm,∠ACB=90°,
∴在Rt△ABC中,AB= = =10 cm.
当∠EAB=90°时,在Rt△EAB和Rt△ECA中,
AE2=EB2-AB2=(EC+8)2-102,
AE2=EC2+AC2=EC2+62,
∴(EC+8)2-102=EC2+62,
∴EC=4.5 cm,
∴BE=BC+CE=12.5 cm;
例2题图②
探究引申
(3)如图③,奇异小组的同学把边BC与边EF重合,连接AD,△ABC固定不动,将△DEF沿射线BC平移,当四边形ACFD是正方形时,直接写出△DEF平移的距离.
例2题图③
【思维教练】分FD在AC右侧和AC左侧两种情况讨论即可求解.
【解法提示】当FD在AC的右侧时,由题意可知,四边形ACFD是矩形,当四边形ACFD为正方形时,即AC=FC=6,∵BC=8,∴平移距离为8-6=2 cm;当FD在AC的左侧时,即AC=FC=6,∴平移距离为8+6=14 cm.综上所述,△DEF平移的距离为2 cm或14 cm.
(3)2 cm或14 cm.
题型四 类比、拓展探究题
(10年8考)
【题型解读】近10年考查8次,其考查类型和频次为:①与图形旋转有关的探究考查6次;②与动点有关的探究考查2次.
类型一 与图形旋转有关的探究
典例精讲
例1 (1)观察猜想
如图①,在Rt△ABC中,∠ACB=90°,AC=BC, 在Rt△BDE中,∠BDE=90°,BD=DE,连接AE,取AE边的中点P,连接DP、CP.
例1题图①
填空:①DP与CP的数量关系是________;
②DP与CP的位置关系是____________;
【思维教练】①要求DP与CP的数量关系,通过直角三角形的性质:斜边上的中线等于斜边的一半,即可得到CP= AE,DP= AE,即可求解;②要求DP与CP的位置关系,
即求∠DPC的度数,通过等腰三角形性质
和三角形的内外角关系,得到∠DPC=2∠BAC,
通过题干得到∠BAC的度数,即可求解.
例1题图①
【解法提示】
∵∠ACB=90°,点P为AE的中点,∴PC为Rt△AEC斜边AE的中线,∴CP= AE,同理可证,DP= AE,∴DP=CP;
∴∠DPE=2∠DAE,∠CPE=2∠CAE,
∵AC=BC,∴∠BAC=45°,∴∠DPC=2∠BAC=90°,∴DP⊥CP.
填空:①DP与CP的数量关系是________;
②DP与CP的位置关系是________;
DP=CP
DP⊥CP
例1题图①
(2)类比探究
把△BDE绕点B逆时针旋转45°至如图②的位置,(1)中的结论是否仍然成立?若成立,请就图②的情形给出证明;若不成立,请说明理由;
例1题图②
【思维教练】要求DP与CP的数量关系和位置关系,过点P作AC的垂线,并构造出DP与PC所在的两个直角三角形,结合旋转的性质可证明DP和PC所在的两个三角形全等,即可求解.
(1)中的结论仍然成立.
证明:如解图①,过点P作MN⊥AC于点N,交BD的延长线于点M,
易得四边形BCNM为矩形,
∴CN=BM.
∵等腰Rt△BDE绕点B逆时针旋转45°,
∴∠MBA=45°,
∴MP=BM,
∴MP=CN,
例1题解图①
N
M
∵∠EDB=90°,∠PMB=90°,
∴DE∥MN,∴ ,
∵点P为AE的中点,
∴AP=EP= PN= MD,∴MD=PN,
∵∠DMP=∠PNC=90°,
∴△PMD≌△CNP,∴DP=CP,∠DPM=∠PCN,
∵∠PCN+∠CPN=90°,
∴∠DPM+∠CPN=90°,∴∠DPC=90°,
∴DP⊥CP;
例1题解图①
N
M
(3)问题解决
若BC=3BD=3 ,将图①中△BDE绕点B在平面内自由旋转,当BE⊥AB时,直接写出线段CP的长.
例1题图①
【思维教练】分△BDE在BC的上方和下方两种情况讨论,利用(2)中的结论可得△PCD为等腰直角三角形,结合题意即可求解.
【解法提示】分两种情况讨论:①如解图②,
由(2)可知DP⊥CP,DP=CP,∴△PCD为等腰直角三角形,
∵BC=3BD=3 ,∴CD=BD+BC=4 ,∴PC=4;
例1题解图②
例1题解图③
②如解图③,由(2)可知DP⊥CP,DP=CP,
∴△PCD为等腰直角三角形,
∵BC=3BD=3 ,∴CD=BC-BD=2 ,∴CP=2.
综上所述,CP的长为4或2.
(3)CP的长为4或2.
类型二 与动点有关的探究
典例精讲
例1 如图,在正方形ABCD中,点E,F分别在射线CD,BC 上,且BF=CE,过点C作CG⊥EF,垂足为点G,CG交射线DB于点H.
(1)如图①,当点E是线段CD的中点,点 F在线段BC上时,线段CH与EF之间的数量关系为____________;
例1题图①
【思维教练】要求CH与EF之间的数量关系,观察图象可知,故考虑CH,EF与BD之间的数量关系,利用三角形中位线的性质即可求出EF= BD,再利用直角三角形中线的性质可求出CH= BD,等量代换即可求出线段CH与EF之间的数量关系.
例1题图①
【解法提示】∵点E是线段CD的中点,∴CE=ED.
∵BC=CD,BF=CE,∴BF=CF,
∴EF∥BD,EF= BD.
∵CG⊥EF,∴CH⊥BD.
∵四边形ABCD是正方形,∴CH= BD,∴CH=EF.
(1)如图①,当点E是线段CD的中点,点 F在线段BC上时,线段CH与EF之间的数量关系为________;
例1题图①
CH=EF
(2)如图②,当点E,F分别在线段CD,BC的延长线上时,判断(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
例1题图②
例1题图②
【思维教练】在CE上截取CM=CF,通过构造△HBC≌△FME,利用全等三角形的性质即可证得CH=EF.
证明:如解图①,在CE上截取CM=CF,连接MF,
(2)成立
M
∵BF=CE,∴BF-CF=CE-CM,∴BC=EM.
∵∠FCM=90°,FC=MC,
∴∠CMF=45°,∴∠FME=135°.
∵∠DBC=45°,
∴∠HBC=135°,∴∠HBC=∠FME.
∵CG⊥EF,
∴∠CGE=90°,
∴∠CEG+∠ECG=90°.
∵∠HCB+∠BCD+∠ECG=180°,∠BCD=90°,
∴∠HCB+∠ECG=90°,
∴∠HCB=∠GEC,
∴△HBC≌△FME(ASA),
∴CH=EF;
例1题图②
M
(3)已知正方形ABCD的边长为6,BH=2 ,请直接写出线段EF的长.
备用图
【思维教练】分点H在对角线BD上和点H在DB的延长线上两种情况进行讨论.
例题解图②
例题解图③
【解法提示】如解图②和解图③,连接AC交BD于点O,则OB=OC=3 ,
∵OH=OB-BH,
∴OH=3 -2 = .
在△OHC中,∠COH=90°,
由勾股定理得CH= .
∵四边形ABCD是正方形,
∴BC=CD,∴∠HBC=45°.
分两种情况讨论:
①如解图②,当点H在对角线BD上时, 延长DC至点M,使CM=CF,连接FM.
例题解图②
∵CF=CM,∴∠FME=45°.
∵CG⊥EF,
∴∠CFE+∠HCF=90°,
又∵∠CEF+∠CFE=90°,
∴∠CEF=∠HCB.
∵BF=CE,CF=CM,∴BC=EM,
∴△BHC≌△MFE,
∴EF=CH=2 ;
例题解图②
②如解图③,当点H在线段DB的延长线上时,
例题解图③
∵OH=OB+BH,
∴OH=3 +2 =5 .
在△OHC中,∠COH=90°,
由勾股定理得CH= ,
由(2)得EF=CH,
∴EF=CH=2 .
综上所述,EF的长为2 或2 .
类型三 与折叠、平移有关的探究
典例精讲
例1 在矩形ABCD中,BC= CD,点E、F分别是边AD、BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.
(1)如图①,当EH与线段BC交于点P时,求证:PE=PF;
例1题图①
【思维教练】由折叠的性质可得∠PEF=∠FED,由矩形的性质可得AD∥BC,进而得到∠FED=∠EFP,通过等量代换可得∠PEF=∠EFP,进而通过等角对等边即可求证PE=PF.
(1)证明:根据折叠性质,∠PEF=∠FED,
∵AD∥BC,
∴∠FED=∠EFP,
∴∠PEF=∠EFP,
∴PE=PF;
例1题图①
(2)如图②,当点P在线段CB的延长线上时,GH交AB于点M,求证:点M在线段EF的垂直平分线上;
例1题图②
【思维教练】由矩形的性质及折叠的性质,结合题目条件可得EH=BF,由(1)进而可得PH=PB,再通过构造Rt△MHE≌Rt△MBF可得ME=MF,进而可证点M在线段EF的垂直平分线上.
∵AD=BC,AE=CF,
∴ED=BF,∴EH=BF,
又∵由(1)知PE=PF,
∴PH=PB,
∵∠PHM=∠PBM=90°,PM是公共边,
∴Rt△PHM≌Rt△PBM,∴HM=BM,
∴Rt△MHE≌Rt△MBF,∴ME=MF,
∴点M在线段EF的垂直平分线上;
(2)证明:如解图①,连接PM、EM、FM,
例1题解图①
(3)当AB=5时,在点E由点A移动到AD中点的过程中,计算出点G运动的路线长.
备用图
【思维教练】通过观察可知,点E从点A移动到AD中点的过程中,点G运动的路线是以矩形中心到点C的距离为半径的圆周长的 ,进而通过弧长公式即可求出点G运动的路线长.
(3)解:如解图②,连接AC,BD,交点为O,连接OG,点E从点A移动到AD中点的过程中,点G运动路径是 ,
在Rt△BCD中,∵BC= CD,
∴tan∠CBD= ,
∴∠CBD=30°,∠ABO=60°,
∴△AOB是等边三角形,
∴OB=OC=AB=5,∠BOC=120°,
∴点G运动的路线长= = .
例1题解图②
例2 综合与探究
问题情境
在数学活动课上,老师让同学们准备两张全等的直角三角形纸片,Rt△ABC≌Rt△DEF,AC=DF=6 cm,BC=EF=8 cm,∠ACB=∠DFE=90°.
实践操作
(1)如图①,把Rt△ABC和Rt△DEF的直角边
BC和EF部分重合,使点E,C,F,B在同一
条直线上,连接AE和BD,得到四边形AEDB.
请说明四边形AEDB的形状并证明;
例2题图①
【思维教练】根据Rt△ABC≌Rt△DEF可得AB=ED,∠ABC=∠BED,进而可得AB∥DE,即可得到四边形AEDB的形状.
(1)解:四边形AEDB是平行四边形.
证明:∵Rt△ABC≌Rt△DEF,
∴AB=ED,∠ABC=∠BED.
∴AB∥ED.
∴四边形AEDB是平行四边形;
例2题图①
实践探究
(2)勤奋小组的同学在图①的基础上,将△DEF沿射线BC平移,其中△ABC不动,得到的四边形AEDB是矩形,如图②,请求出此时BE的长;
例2题图②
【思维教练】根据已知条件,在Rt△ABC中可求出AB的长,进而在Rt△ABE和Rt△ECA中,由勾股定理即可求解.
(2)∵四边形AEDB是矩形,∴∠EAB=90°.
∵AC=6 cm,BC=8 cm,∠ACB=90°,
∴在Rt△ABC中,AB= = =10 cm.
当∠EAB=90°时,在Rt△EAB和Rt△ECA中,
AE2=EB2-AB2=(EC+8)2-102,
AE2=EC2+AC2=EC2+62,
∴(EC+8)2-102=EC2+62,
∴EC=4.5 cm,
∴BE=BC+CE=12.5 cm;
例2题图②
探究引申
(3)如图③,奇异小组的同学把边BC与边EF重合,连接AD,△ABC固定不动,将△DEF沿射线BC平移,当四边形ACFD是正方形时,直接写出△DEF平移的距离.
例2题图③
【思维教练】分FD在AC右侧和AC左侧两种情况讨论即可求解.
【解法提示】当FD在AC的右侧时,由题意可知,四边形ACFD是矩形,当四边形ACFD为正方形时,即AC=FC=6,∵BC=8,∴平移距离为8-6=2 cm;当FD在AC的左侧时,即AC=FC=6,∴平移距离为8+6=14 cm.综上所述,△DEF平移的距离为2 cm或14 cm.
(3)2 cm或14 cm.
同课章节目录
