3.4 函数的应用(一)课件(共51张PPT)——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.4 函数的应用(一)课件(共51张PPT)——高中数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 711.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-17 11:27:46 | ||
图片预览










文档简介
(共51张PPT)
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律,提升数学建模、数据分析和数学运算素养.
1
知识梳理
自主探究
1.一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型,一次函数的图象为直线,应用一次函数的性质,可以求参数值及函数解析式等.
2.二次函数模型
(1)形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型.
(2)二次函数模型是生活中最常见的一种数学模型,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时可以依据二次函数的单调性求最值,从而解决最大、最小等问题.
3.分段函数模型
(1)分段函数模型.
分段函数是指函数解析式由几段组成的函数,根据自变量取值范围的不同,由题设确定出不同的函数关系式.
(2)分段函数模型的应用.
①分段函数模型应用的关键是确定分段的各边界点.即明确自变量的取值区间,对每一区间进行分类讨论,从而写出函数解析式,需注意分段函数的最值,是各区间上解析式取得的最大值或最小值.
②要注意结合实际问题的实际意义,有时还可结合图象去求解.
2
师生互动
合作探究
一次函数模型
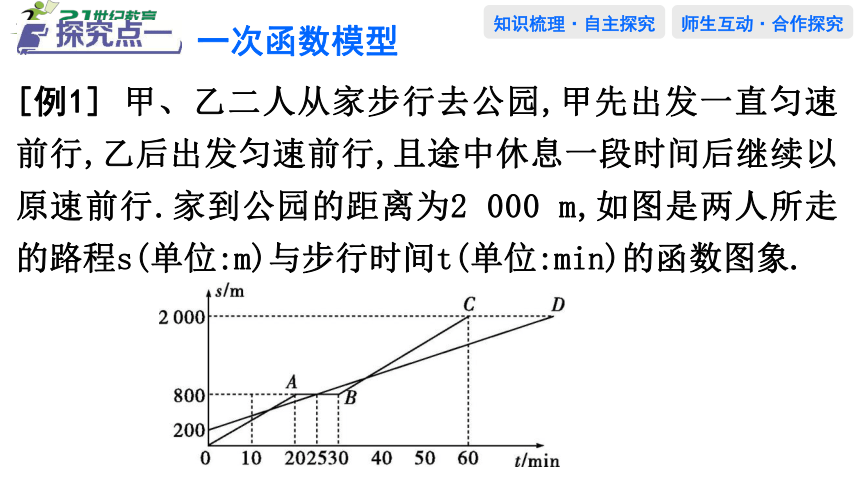
[例1] 甲、乙二人从家步行去公园,甲先出发一直匀速前行,乙后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2 000 m,如图是两人所走的路程s(单位:m)与步行时间t(单位:min)的函数图象.
(1)求BC段图象所对应的函数关系式;
(2)乙出发多长时间与甲第三次相遇
(3)在速度都不变的情况下,乙希望比甲早18 min到达公园,则乙在步行过程中停留的时间需减少多少min
解:(3)当s=2 000时,2 000=24t+200,得t=75,
因为75-60=15,
所以乙希望比甲早18 min到达公园,
则乙在步行过程中停留的时间需要减少3 min.
建立一次函数模型,常设为y=kx+b(k≠0),然后用待定系数法求出k,b的值,再根据单调性求最值或利用方程、不等式思想解题.
针对训练1:为了保护学生的视力,课桌和椅子的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为y cm,椅子的高度为x cm,则y应是x的一次函数,现列出两套符合条件的课桌和椅子的高度如表:
第一套 第二套
椅子高度x/cm 40.0 37.0
课桌高度y/cm 75.0 70.2
(1)请你确定y与x的函数关系式(不必写出x的取值范围);
(2)现有一把高42.0 cm的椅子和一张高78.2 cm的课桌,它们是否配套 为什么
解:(2)把x=42代入上述函数解析式中,
得y=1.6×42+11=78.2,
所以给出的这套桌椅是配套的.
二次函数模型
[例2] 某农家旅游公司有客房160间,每间房单价为
200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间,若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
解:设每间房单价提高x个20元时,每天客房的租金总收入为y元.
此时每间房单价为(200+20x)元,而客房出租数将减少10x间,即为(160-10x)间,因此
y=(200+20x)(160-10x)=200(10+x)(16-x)
=200(-x2+6x+160)=200[-(x-3)2+169]
=-200(x-3)2+33 800.
从而可知,当x=3时,y的最大值为33 800.
因此每间房单价提到200+20×3=260(元)时,每天客房的租金总收入最高.
(1)二次函数与二次方程之间有密切的关系,解题时要注意题目中的约束条件.
(2)求解二次函数问题应注意二次函数图象的对称性与单调性.
(3)解决实际生活中用料最省、利润最大等问题时,一般建立二次函数模型,还需掌握一些常见的关系式,如利润=
(商品销售单价-商品成本单价)×销售量等.
针对训练2:某公司试销一种成本单价为50元/件的新产
品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图
所示).
(1)根据图象,求一次函数y=kx+b的解析式;
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
①试用销售单价x表示利润S;
解:(2)①由(1)知,S=xy-50y=(-x+100)(x-50)
=-x2+150x-5 000(50≤x≤80).
②当销售单价定为多少时,该公司可获得最大利润 最大利润是多少 此时的销售量是多少
解:②由①可知,S=-(x-75)2+625(50≤x≤80),
其图象开口向下,对称轴为直线x=75,
所以当x=75时,Smax=625,
即该公司可获得的最大利润为625元,
此时相应的销售单价为75元/件,销售量为25件.
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(1)将两个养殖池的总面积y表示为x的函数,并写出定义域;
(2)当温室的边长x取何值时,总面积y最大 最大面积是多少
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/m,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(1)用x表示修建储物间的总造价f(x)(单位:元);
(2)如何设计该储物间,可使总造价最低 最低总造价为多少元
分段函数模型
当0当25≤t≤30,t∈N,t=25时,ymax=1 125(元).
因为1 125>900,所以ymax=1 125.
所以这种商品的日销售金额的最大值为1 125元,
第25天日销售金额最大.
应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的
并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后取并集.
(1)请将利润y(单位:元)表示成关于月产量x(单位:件)的函数;
(2)当月产量为多少时,利润最大 最大利润是多少
1
2
3
4
√
1.随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,且含氧量y(单位:g/m3)与大气压强x(单位:
kPa)成正比例函数关系.当x=36时,y=108,则y与x的函数关系式为( )
1
2
3
4
解析:由题意设y=kx(k≠0),将(36,108)代入解析式可得k=3,故y=3x,考虑到含氧量不可能为负,可知x≥0.故选A.
2.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6 s B.4 s C.3 s D.2 s
1
2
3
4
√
解析:令h=30t-5t2=0,得t=0(舍去)或t=6.故小球从抛出至回落到地面所需要的时间是6 s.故选A.
1
2
3
4
A.135 B.149 C.165 D.195
√
1
2
3
4
A.15 B.40
C.25 D.13
1
2
3
4
√
1
2
3
4
解析:令y=60,若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.故拟录用人数为25.故选C.
[例1] (多选题)已知每生产100 g饼干的原材料加工费为1.8元,某食品加工厂对饼干采用两种包装,其包装费用、销售价格如表所示.
型号 小包装 大包装
质量 100 g 300 g
包装费 0.5元 0.7元
销售价格 3.0元 8.4元
则下列说法正确的是( )
A.买小包装实惠 B.买大包装实惠
C.卖3小包比卖1大包盈利多 D.卖1大包比卖3小包盈利多
√
√
解析:大包装300 g8.4元,则等价为100 g2.8元,小包装100 g3元,则买大包装实惠,故B正确;卖1大包的盈利8.4-0.7-1.8×3=2.3(元),卖1小包盈利3-0.5-1.8=
0.7(元),则卖3小包盈利0.7×3=2.1(元),则卖1大包比卖3小包盈利多,故D正确.故选BD.
[例2] (多选题)某公司一年购买某种货物900 t,现分次购买,若每次购买x t,运费为9万元/次,一年的总储存费用为4x万元,要使一年的总运费与总储存费用之和最小,则下列说法正确的是( )
A.x=10时费用之和有最小值
B.x=45时费用之和有最小值
C.总费用最小为850万元
D.总费用最小为360万元
√
√
[例3] 某校高一(1)班共有学生50人,据统计,原来每人每年用于购买饮料的平均支出是a元.经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成:一部分是购买纯净水的费用,另一部分是其他费用780元,其中纯净水的销售价x(单位:元/桶)与年购买总量y(单位:桶)之间满足如图所示的关系.
(1)求x与y的函数关系式;
(2)当a为120时,若该班每年需要纯净水380桶,请你根据提供的信息分析,该班学生集体改饮桶装纯净水与个人买饮料相比,哪一种花钱更少
解:(2)当a=120时,若购买饮料,则总费用为120×50=6 000(元);
若集体改饮桶装纯净水,设所用的费用为ω元,由380=-80x+720,得x=4.25.
所以ω=380×4.25+780=2 395(元)<6 000(元).
所以该班学生集体改饮桶装纯净水更省钱.
3.4 函数的应用(一)
学习目标
1.理解函数是描述客观世界中变量关系和规律的重要数学语言和工具.
2.在实际情境中,会选择合适的函数模型刻画现实问题的变化规律,提升数学建模、数据分析和数学运算素养.
1
知识梳理
自主探究
1.一次函数模型
形如y=kx+b(k≠0)的函数模型是一次函数模型,一次函数的图象为直线,应用一次函数的性质,可以求参数值及函数解析式等.
2.二次函数模型
(1)形如y=ax2+bx+c(a≠0)的函数模型是二次函数模型.
(2)二次函数模型是生活中最常见的一种数学模型,依据实际问题建立二次函数的解析式后,利用配方法求最值简单易懂,有时可以依据二次函数的单调性求最值,从而解决最大、最小等问题.
3.分段函数模型
(1)分段函数模型.
分段函数是指函数解析式由几段组成的函数,根据自变量取值范围的不同,由题设确定出不同的函数关系式.
(2)分段函数模型的应用.
①分段函数模型应用的关键是确定分段的各边界点.即明确自变量的取值区间,对每一区间进行分类讨论,从而写出函数解析式,需注意分段函数的最值,是各区间上解析式取得的最大值或最小值.
②要注意结合实际问题的实际意义,有时还可结合图象去求解.
2
师生互动
合作探究
一次函数模型
[例1] 甲、乙二人从家步行去公园,甲先出发一直匀速前行,乙后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2 000 m,如图是两人所走的路程s(单位:m)与步行时间t(单位:min)的函数图象.
(1)求BC段图象所对应的函数关系式;
(2)乙出发多长时间与甲第三次相遇
(3)在速度都不变的情况下,乙希望比甲早18 min到达公园,则乙在步行过程中停留的时间需减少多少min
解:(3)当s=2 000时,2 000=24t+200,得t=75,
因为75-60=15,
所以乙希望比甲早18 min到达公园,
则乙在步行过程中停留的时间需要减少3 min.
建立一次函数模型,常设为y=kx+b(k≠0),然后用待定系数法求出k,b的值,再根据单调性求最值或利用方程、不等式思想解题.
针对训练1:为了保护学生的视力,课桌和椅子的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为y cm,椅子的高度为x cm,则y应是x的一次函数,现列出两套符合条件的课桌和椅子的高度如表:
第一套 第二套
椅子高度x/cm 40.0 37.0
课桌高度y/cm 75.0 70.2
(1)请你确定y与x的函数关系式(不必写出x的取值范围);
(2)现有一把高42.0 cm的椅子和一张高78.2 cm的课桌,它们是否配套 为什么
解:(2)把x=42代入上述函数解析式中,
得y=1.6×42+11=78.2,
所以给出的这套桌椅是配套的.
二次函数模型
[例2] 某农家旅游公司有客房160间,每间房单价为
200元时,每天都客满.已知每间房单价每提高20元,则客房出租数就会减少10间,若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高
解:设每间房单价提高x个20元时,每天客房的租金总收入为y元.
此时每间房单价为(200+20x)元,而客房出租数将减少10x间,即为(160-10x)间,因此
y=(200+20x)(160-10x)=200(10+x)(16-x)
=200(-x2+6x+160)=200[-(x-3)2+169]
=-200(x-3)2+33 800.
从而可知,当x=3时,y的最大值为33 800.
因此每间房单价提到200+20×3=260(元)时,每天客房的租金总收入最高.
(1)二次函数与二次方程之间有密切的关系,解题时要注意题目中的约束条件.
(2)求解二次函数问题应注意二次函数图象的对称性与单调性.
(3)解决实际生活中用料最省、利润最大等问题时,一般建立二次函数模型,还需掌握一些常见的关系式,如利润=
(商品销售单价-商品成本单价)×销售量等.
针对训练2:某公司试销一种成本单价为50元/件的新产
品,规定试销时销售单价不低于成本单价,又不高于80元/件.经试销调查,发现销售量y(单位:件)与销售单价x(单位:元/件)的关系可近似看作一次函数y=kx+b(如图
所示).
(1)根据图象,求一次函数y=kx+b的解析式;
(2)设公司获得的利润为S(单位:元)(利润=销售总价-成本总价,销售总价=销售单价×销售量,成本总价=成本单价×销售量).
①试用销售单价x表示利润S;
解:(2)①由(1)知,S=xy-50y=(-x+100)(x-50)
=-x2+150x-5 000(50≤x≤80).
②当销售单价定为多少时,该公司可获得最大利润 最大利润是多少 此时的销售量是多少
解:②由①可知,S=-(x-75)2+625(50≤x≤80),
其图象开口向下,对称轴为直线x=75,
所以当x=75时,Smax=625,
即该公司可获得的最大利润为625元,
此时相应的销售单价为75元/件,销售量为25件.
[例3] 现计划建造一个室内面积为1 500 m2的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留1.5 m宽的通道,两养殖池之间保留2 m宽的通道.设温室的一边长度为x m,如图所示.
(1)将两个养殖池的总面积y表示为x的函数,并写出定义域;
(2)当温室的边长x取何值时,总面积y最大 最大面积是多少
针对训练3:某建筑公司打算在一处工地上修建一座简易储物间.该储物间室内地面呈矩形形状,面积为50 m2,并且一面紧靠工地现有围墙,另三面用高度一定的矩形彩钢板围成,顶部用防雨布遮盖,其平面图如图所示.已知该型号彩钢板价格为100元/m,整理地面及防雨布总费用为500元,不受地形限制,不考虑彩钢板的厚度,记与墙面平行的彩钢板的长度为x m.
(1)用x表示修建储物间的总造价f(x)(单位:元);
(2)如何设计该储物间,可使总造价最低 最低总造价为多少元
分段函数模型
当0
因为1 125>900,所以ymax=1 125.
所以这种商品的日销售金额的最大值为1 125元,
第25天日销售金额最大.
应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的
并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后取并集.
(1)请将利润y(单位:元)表示成关于月产量x(单位:件)的函数;
(2)当月产量为多少时,利润最大 最大利润是多少
1
2
3
4
√
1.随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,且含氧量y(单位:g/m3)与大气压强x(单位:
kPa)成正比例函数关系.当x=36时,y=108,则y与x的函数关系式为( )
1
2
3
4
解析:由题意设y=kx(k≠0),将(36,108)代入解析式可得k=3,故y=3x,考虑到含氧量不可能为负,可知x≥0.故选A.
2.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( )
A.6 s B.4 s C.3 s D.2 s
1
2
3
4
√
解析:令h=30t-5t2=0,得t=0(舍去)或t=6.故小球从抛出至回落到地面所需要的时间是6 s.故选A.
1
2
3
4
A.135 B.149 C.165 D.195
√
1
2
3
4
A.15 B.40
C.25 D.13
1
2
3
4
√
1
2
3
4
解析:令y=60,若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.故拟录用人数为25.故选C.
[例1] (多选题)已知每生产100 g饼干的原材料加工费为1.8元,某食品加工厂对饼干采用两种包装,其包装费用、销售价格如表所示.
型号 小包装 大包装
质量 100 g 300 g
包装费 0.5元 0.7元
销售价格 3.0元 8.4元
则下列说法正确的是( )
A.买小包装实惠 B.买大包装实惠
C.卖3小包比卖1大包盈利多 D.卖1大包比卖3小包盈利多
√
√
解析:大包装300 g8.4元,则等价为100 g2.8元,小包装100 g3元,则买大包装实惠,故B正确;卖1大包的盈利8.4-0.7-1.8×3=2.3(元),卖1小包盈利3-0.5-1.8=
0.7(元),则卖3小包盈利0.7×3=2.1(元),则卖1大包比卖3小包盈利多,故D正确.故选BD.
[例2] (多选题)某公司一年购买某种货物900 t,现分次购买,若每次购买x t,运费为9万元/次,一年的总储存费用为4x万元,要使一年的总运费与总储存费用之和最小,则下列说法正确的是( )
A.x=10时费用之和有最小值
B.x=45时费用之和有最小值
C.总费用最小为850万元
D.总费用最小为360万元
√
√
[例3] 某校高一(1)班共有学生50人,据统计,原来每人每年用于购买饮料的平均支出是a元.经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成:一部分是购买纯净水的费用,另一部分是其他费用780元,其中纯净水的销售价x(单位:元/桶)与年购买总量y(单位:桶)之间满足如图所示的关系.
(1)求x与y的函数关系式;
(2)当a为120时,若该班每年需要纯净水380桶,请你根据提供的信息分析,该班学生集体改饮桶装纯净水与个人买饮料相比,哪一种花钱更少
解:(2)当a=120时,若购买饮料,则总费用为120×50=6 000(元);
若集体改饮桶装纯净水,设所用的费用为ω元,由380=-80x+720,得x=4.25.
所以ω=380×4.25+780=2 395(元)<6 000(元).
所以该班学生集体改饮桶装纯净水更省钱.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
