阶段性综合复习训练(考查内容:第6章、第7章)(含解析)2023——2024学年高中数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 阶段性综合复习训练(考查内容:第6章、第7章)(含解析)2023——2024学年高中数学苏教版(2019)选择性必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 21:01:42 | ||
图片预览




文档简介
阶段性综合复习训练(考查内容:第6章、第7章)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知向量,,若,则( )
A. B. C.4 D.2
2.已知向量,,则向量在向量上的投影向量( )
A. B.
C. D.
3.设与为两个正四棱锥,正方形ABCD的边长为且,点M在线段AC上,且,将异面直线PD,QM所成的角记为,则的最小值为( )
A. B. C. D.
4.如图,在四棱锥中,底面为菱形,,,为棱的中点,且,则( )
A. B.0 C.2 D.4
5.将5名实习老师安排到高一年级的3个班实习,每班至少1人、至多2人,则不同的安排方法有( )
A.90种 B.120种
C.150种 D.18种
6.现有四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为( )
A. B. C. D.
7.展开式中的常数项是( )
A. B. C. D.
8.现有一个6行5列的矩形阵,现有甲、乙、丙三人,要求该三人不在同一行也不在同一列,则不同的站法有( )种
A.1200 B.7200 C.3600 D.900
二、多选题
9.如图,已知二面角的棱上有,两点,,,,,且,则下列说法正确的是( )
A.
B.当二面角的大小为时,
C.若,则与所成的角的余弦是
D.若,则二面角的余弦值为
10.在空间直角坐标系O-xyz中,以下结论正确的是( )
A.点关于x轴对称的点的坐标为(-1,-3,4)
B.点关于xOy平面对称的点的坐标为(-1,2,-3)
C.点关于原点对称的点的坐标为(3,-1,-5)
D.两点间的距离为3
11.在主题为“爱我中华”的演讲比赛中,参赛者甲、乙、丙、丁、戊进入了前5名的决赛(获奖名次不重复)、甲、乙、丙三人一起去询问成绩,回答者说:“甲、乙两人之中有一人的成绩为第三人名,丙的成绩不是第五名."根据这个回答,下列结论正确的有( )
A.五人名次排列的所有情况共有36种
B.甲、乙的排名不相邻的所有情况共有24种
C.甲、乙的排名均高于丙的排名的所有情况共有8种
D.丙的排名高于甲的排名的所有情况共有24种
12.若且,则( )
A. B.
C. D.
三、填空题
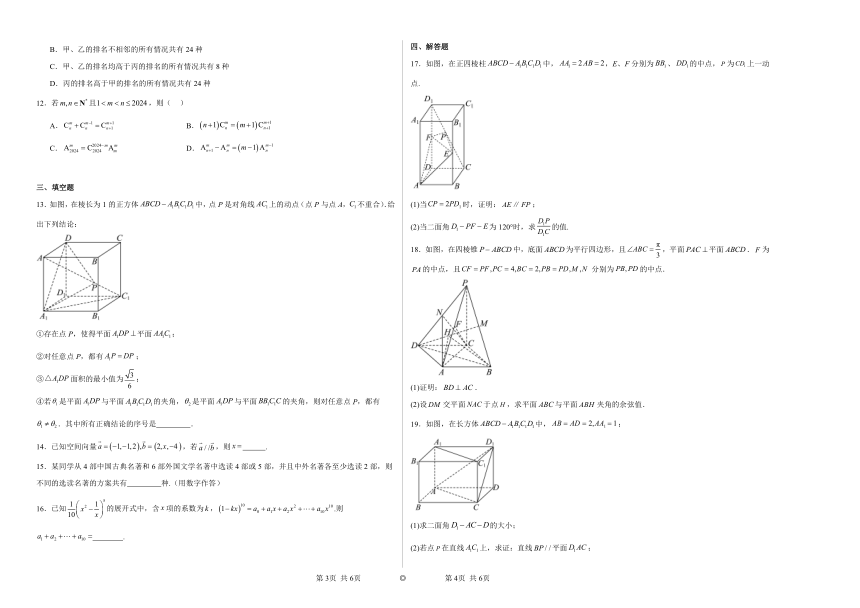
13.如图,在棱长为1的正方体中,点P是对角线上的动点(点P与点A,不重合).给出下列结论:
①存在点P,使得平面平面;
②对任意点P,都有;
③面积的最小值为;
④若是平面与平面的夹角,是平面与平面的夹角,则对任意点P,都有.其中所有正确结论的序号是 .
14.已知空间向量,若,则 .
15.某同学从4部中国古典名著和6部外国文学名著中选读4部或5部,并且中外名著各至少选读2部,则不同的选读名著的方案共有 种.(用数字作答)
16.已知的展开式中,含项的系数为,.则 .
四、解答题
17.如图,在正四棱柱中,,E、F分别为、的中点,为上一动点.
(1)当时,证明:;
(2)当二面角为120°时,求的值.
18.如图,在四棱锥中,底面为平行四边形,且,平面平面.为的中点,且分别为的中点.
(1)证明:.
(2)设交平面于点,求平面与平面夹角的余弦值.
19.如图,在长方体中,;
(1)求二面角的大小;
(2)若点在直线上,求证:直线平面;
20.某大学A学院共有学生千余人,该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,已知A学院男生与女生人数之比为,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
跑步里程s()
男生 9 10 6
女生 6 6 4 2
用样本频率估计总体概率,
(1)求a的值,并估计从A学院所有学生中抽取一人,该学生5月份累计跑步里程()在中的概率;
(2)从A学院所有男生中随机抽取2人,从A学院所有女生中随机抽取2人,估计这4人中恰有2人在5月份的累计跑步里程不低于的概率;
(3)该大学B学院男生与女生人数之比为,B学院体育社团为了解学生参与跑步运动的情况,也按性别进行分层抽样已知A学院和B学院的样本数据整理如下表.
5月份累计跑步里程平均值(单位:)
学院性别 A B
男生 50 59
女生 40 45
设A学院样本中学生5月份累计跑步里程平均值为,B学院样本中学生5月份累计跑步里程平均值为,是否存在,使得 如果存在,求的最大值;如果不存在,说明理由.
21.现有4名男生和3名女生.
(1)若安排这7名学生站成一排照相,要求3名女生互不相邻,这样的排法有多少种?
(2)若邀请这7名学生中的4名参加一项活动,其中男生甲和女生乙不能同时参加,求邀请的方法种数;
(3)若将这7名学生全部安排到5个备选工厂中的4个工厂参加暑期社会实践活动,要求3名女生必须安排在同一个工厂,求这样安排的方法共有多少种?
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据空间共线向量的坐标表示建立方程组,解之即可求解.
【详解】由,知,使得,
即,所以,
解得,所以.
故选:B
2.C
【分析】根据给定条件,利用投影向量的意义求解即得.
【详解】由向量,,得,而,
向量在向量上的投影向量.
故选:C
3.A
【分析】建立适当空间站直角坐标系后,借助空间向量表示出的余弦值,结合基本不等式计算即可得解.
【详解】连接交于点,以为坐标原点,建立如图所示的空间直角坐标系,
因为正方形的边长为,所以,
因为,所以为的中点,
设,在直角中,有,故,
所以,
则,
所以,
因为,
当且仅当,即时等号成立,所以的最大值为,
因此的最小值为.
故选:A.
4.C
【分析】首先分析题意,作,建立空间直角坐标系,设出对应点的坐标建立方程,整体代换求解即可.
【详解】作,以A为原点建立如图所示空间直角坐标系,
,
,,
,即
,即C正确,
故选:C.
5.A
【分析】先将5名实习老师按1人、2人、2人分为三组,再安排到3个班中,由排列组合计数求解即可.
【详解】由题意,先将5名实习老师按1人、2人、2人分为三组,再安排到3个班中,
则不同的安排方法有(种).
故选:A.
6.C
【分析】根据题意,由分步计数原理计算“用四种不同得颜色要对如图形中的五部分进行着色”和“任意有公共边的两块着不同颜色”的涂色方法,由古典概型公式计算可得答案.
【详解】根据题意,用四种不同的颜色要对如图形中的五个部分进行着色,每个部分都有4种涂色方法,则有种涂色方法;
若其中任意有公共边的两块着不同颜色,有两种情况:①只用三种颜色涂这5个区域,则有种涂色方法;②用四种颜色涂这5个区域,则有种涂色方法,所以若其中任意有公共边的两块着不同颜色,共有144种涂色方法,故四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为.
故选:C
7.D
【分析】由,写出展开式的通项,即可求出展开式中的常数项.
【详解】因为,
其中展开式的通项为(且),
令,得,∴,
故展开式中的常数项是.
故选:D.
8.B
【分析】利用分步计数原理结合排列组合知识解决.
【详解】事件甲,乙,丙三人不在同一行也不在同一列可分为四步完成,
第一步,从6行中任选三行,共有种方法,
第二步,从所选的三行的15个位置中选一个位置排甲,共有15种方法,
第三步,从余下可选的8个位置中选一个位置排乙,共有8种方法,
第四步,从余下可选的3个位置中选一个位置排丙,共有3种方法,
由分步乘法计数原理可得,
三人不在同一行也不在同一列的不同的站法有种,
故选:B
9.ABD
【分析】由空间向量的数量积运算计算判断A;由数量积的运算律计算判断B;由利用空间向量求出异面直线夹角的余弦判断C;由几何法求出二面角的余弦判断D.
【详解】二面角中,,于,于,,
对于A,,A正确;
对于B,由二面角的大小为,得,
则
,B正确;
对于C,由选项A知,,则与所成的角的余弦为,C错误;
对于D,过作,且使,连接,则四边形是正方形,
有,,而平面,则平面,
又平面,因此,即,由,得,
所以为等边三角形,取中点,连接,则,,
取中点,连接,,有,
又平面,则平面,又平面,则,
因此为二面角的平面角,又,,
显然,即,则,D正确.
故选:ABD
10.BCD
【分析】结合空间直角坐标系的对称关系可判断A,B,C;结合两点间距离公式可求D.
【详解】点关于x轴的对称点的坐标为,故A错误;
点关于xOy平面对称的点的坐标为,故B正确;
关于原点的对称的点的坐标为,故C正确;
两点间的距离为,故D正确.
故选:BCD
11.ACD
【分析】由分步乘法计算可得AC正确;由分类加法和分步乘法计算可得B错误;分丙在第一,第二,第四三种情况用分类加法和分步乘法计算得到D正确.
【详解】A:甲、乙两人之中有一人的成绩为第三人名有种情况,丙的成绩不是第五名有种,剩下全排,所以共有种,故A正确;
B:设甲排在第三,乙可在第一和第五;
当乙在第一时,有种;
当乙在第五时,有种,
甲乙可以互换,所以共有种,故B错误;
C:由条件可知,丙只能在第四,
当甲在第三,乙只能在第一,第二的位置共有种,
由于甲乙可以互换,所以共有种,故C正确;
D:丙在第一时,有种;
丙在第二时,分为两种情况,①甲在第三,有种;②乙在第三,甲在第四或五,有种;
丙在第四,甲只能在第五,此时乙在第三,有2种;
所以共有种,故D正确;
故选:ACD.
12.BC
【分析】根据排列数和组合数的公式及性质逐项判断即可.
【详解】由组合数的性质知,故A错误;
因为,,故,故B正确;
由,得,故C正确;
,故D错误.
故选:BC.
13.①②③
【分析】①可通过线面垂直的判定定理找到点P;②③④都可以通过建立空间直角坐标系解决,其中通过向量的长度可以对②进行判断;利用两条直线所成的角和三角形面积公式可以判断③;求出三个面的法向量,并求出和,即可对④进行判断.
【详解】①因为,在上取点使,
因为,平面,所以平面,
因为平面,所以平面平面,故①正确;
②以为原点,以分别为轴建立空间直角坐标系,如图
,,,,则,,
设,则,,
从而,,所以,故②正确;
③由②,,,
,,
当且仅当时等号成立,所以面积的最小值为,故③正确;
④平面的法向量,平面的法向量,
设平面的法向量,
由即得,
令得,
则,,
令得或,而,故,
从而对存在点P,使得,而不大于直角,
故,故④错误;
故答案为:①②③.
14.
【分析】利用空间向量共线的坐标运算,即可求出结果.
【详解】因为,,
所以,解得,
故答案为:.
15.270
【分析】分选读4部名著或选读5部名著2种情况,根据题意结合组合数分析求解.
【详解】若选读4部名著,则不同的选读名著的方案共有种;
若选读5部名著,可知中国古典名著有2部或3部,则不同的选读名著的方案共有种;
所以不同的选读名著的方案共有种.
故答案为:270.
16.1023
【分析】根据二项式展开式的通项公式,结合题意求得,再通过赋值法先求,再求目标即可.
【详解】的展开式的通项公式为,
令,则可得含项的系数,则,
对,令,解得;对,令,解得,
故.
故答案为:.
17.(1)证明见解析
(2)
【分析】(1)建立空间直角坐标系,求出的坐标,用向量共线定理证明结论.
(2)设,进而用参数求出相应平面的法向量,结合已知二面角大小列方程求参数.
【详解】(1)如图:以为原点,建立空间直角坐标系.
则,,,因为为中点,所以,
,,,因为,所以.
所以,,所以,故.
(2)结合二面角大小知:在线段靠近部分,设(),则,
设,则,即.
所以,.
设平面的法向量为,则
,取.
又平面的法向量可以取.
所以,,.
因为二面角为120°.
所以.
结合图形,,所以.
18.(1)证明见解析
(2)
【分析】(1)设与交于点,根据题意,证得和,结合线面垂直的判定定理,证得平面,进而证得.
(2)由(1)知平面,得到平面,以为坐标原点,建立空间直角坐标系,求得平面和平面的法向量和,结合向量的夹角公式,即可求解.
【详解】(1)证明:如图所示,设与交于点,连接,
因为底面是平行四边形,所以为的中点,
又因为,所以,
因为,且为的中点,所以,
又因为平面,且平面平面,平面平面,
所以平面,
因为平面,所以,
又因为,且平面,所以平面,
因为平面,所以.
(2)解:如图所示,连接,因为为的中位线,所以,
因为平面平面且,
所以,且,
由分别为的中点,看到的,
由(1)知平面,所以平面.
以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,
如图所示,则,
所以,则,
设为平面的法向量,则,
取,可得,所以,
又由平面的一个法向量为,
设平面与平面的夹角为,可得.
即平面与平面的夹角余弦值为.
19.(1)
(2)见解析
【分析】(1)以为原点,建立空间直角坐标系,分别求得平面和平面的一个法向量和,结合向量的夹角公式,即可求解.
(2)设,求出,则,再由可证明直线平面.
【详解】(1)以为坐标原点,建立如图所示的空间直角坐标系,
所以,,
因为,
设平面的法向量为,则,
取,可得,所以,
设平面的法向量为
所以,
所以二面角的大小为.
(2)设,则设,,
所以,所以,
平面的法向量为,
,因为平面,
所以直线平面.
20.(1),概率为
(2)
(3)存在满足条件的,且的最大值为
【分析】(1)先根据男女比即可求出,再根据古典概型即可求出所求概率;
(2)先分别求出在A学院所有男生中任取人,跑步里程不低于的概率及在A学院所有女生中任取人,跑步里程不低于的概率,再根据乘法公式求解即可;
(3)设学院女生人数为,则男生人数为,求出,,即可得到不等式,解得即可.
【详解】(1)依题意,解得,
所以在中的概率为;
(2)学院所抽取的学生中男生有人,
其中5月份的累计跑步里程不低于有人,
女生有人,
其中5月份的累计跑步里程不低于有人,
所以在A学院所有男生中任取人,跑步里程不低于的概率为,
在A学院所有女生中任取人,跑步里程不低于的概率为,
所以4人中恰有2人累计跑步里程不低于的概率为
;
(3)设B学院女生有人,则男生有人,
,
,
依题意,即,
显然,解得,所以的最大值为.
21.(1)1440
(2)25
(3)1200
【分析】(1)采用插空法进行求解即可;
(2)采用去杂法进行求解即可;
(3)根据分类加法计数原理,结合排列和组合的定义进行求解即可.
【详解】(1)由题意可知;运用插空法,可得共有排法数为种.
(2)由题意可知:邀请这7名学生中的4名参加一项活动共有种方法,
男生甲和女生乙同时参加的方法有
共有邀请方法数为种.
(3)有两类不同情形:
①先选4个工厂,将3名女生和1名男生安排在同一个工厂,其余3名男生分别在另三个工厂,一厂安排一人,其方法数为种;
②先选4个工厂,将3名女生安排在一个工厂,4名男生安排在另外三个工厂,有一厂两人,另两厂各一人,
其方法数为种.
所以共有种不同的安排方法.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知向量,,若,则( )
A. B. C.4 D.2
2.已知向量,,则向量在向量上的投影向量( )
A. B.
C. D.
3.设与为两个正四棱锥,正方形ABCD的边长为且,点M在线段AC上,且,将异面直线PD,QM所成的角记为,则的最小值为( )
A. B. C. D.
4.如图,在四棱锥中,底面为菱形,,,为棱的中点,且,则( )
A. B.0 C.2 D.4
5.将5名实习老师安排到高一年级的3个班实习,每班至少1人、至多2人,则不同的安排方法有( )
A.90种 B.120种
C.150种 D.18种
6.现有四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为( )
A. B. C. D.
7.展开式中的常数项是( )
A. B. C. D.
8.现有一个6行5列的矩形阵,现有甲、乙、丙三人,要求该三人不在同一行也不在同一列,则不同的站法有( )种
A.1200 B.7200 C.3600 D.900
二、多选题
9.如图,已知二面角的棱上有,两点,,,,,且,则下列说法正确的是( )
A.
B.当二面角的大小为时,
C.若,则与所成的角的余弦是
D.若,则二面角的余弦值为
10.在空间直角坐标系O-xyz中,以下结论正确的是( )
A.点关于x轴对称的点的坐标为(-1,-3,4)
B.点关于xOy平面对称的点的坐标为(-1,2,-3)
C.点关于原点对称的点的坐标为(3,-1,-5)
D.两点间的距离为3
11.在主题为“爱我中华”的演讲比赛中,参赛者甲、乙、丙、丁、戊进入了前5名的决赛(获奖名次不重复)、甲、乙、丙三人一起去询问成绩,回答者说:“甲、乙两人之中有一人的成绩为第三人名,丙的成绩不是第五名."根据这个回答,下列结论正确的有( )
A.五人名次排列的所有情况共有36种
B.甲、乙的排名不相邻的所有情况共有24种
C.甲、乙的排名均高于丙的排名的所有情况共有8种
D.丙的排名高于甲的排名的所有情况共有24种
12.若且,则( )
A. B.
C. D.
三、填空题
13.如图,在棱长为1的正方体中,点P是对角线上的动点(点P与点A,不重合).给出下列结论:
①存在点P,使得平面平面;
②对任意点P,都有;
③面积的最小值为;
④若是平面与平面的夹角,是平面与平面的夹角,则对任意点P,都有.其中所有正确结论的序号是 .
14.已知空间向量,若,则 .
15.某同学从4部中国古典名著和6部外国文学名著中选读4部或5部,并且中外名著各至少选读2部,则不同的选读名著的方案共有 种.(用数字作答)
16.已知的展开式中,含项的系数为,.则 .
四、解答题
17.如图,在正四棱柱中,,E、F分别为、的中点,为上一动点.
(1)当时,证明:;
(2)当二面角为120°时,求的值.
18.如图,在四棱锥中,底面为平行四边形,且,平面平面.为的中点,且分别为的中点.
(1)证明:.
(2)设交平面于点,求平面与平面夹角的余弦值.
19.如图,在长方体中,;
(1)求二面角的大小;
(2)若点在直线上,求证:直线平面;
20.某大学A学院共有学生千余人,该学院体育社团为了解学生参与跑步运动的情况,按性别分层抽样,已知A学院男生与女生人数之比为,从该学院所有学生中抽取若干人作为样本,对样本中的每位学生在5月份的累计跑步里程进行统计,得到下表.
跑步里程s()
男生 9 10 6
女生 6 6 4 2
用样本频率估计总体概率,
(1)求a的值,并估计从A学院所有学生中抽取一人,该学生5月份累计跑步里程()在中的概率;
(2)从A学院所有男生中随机抽取2人,从A学院所有女生中随机抽取2人,估计这4人中恰有2人在5月份的累计跑步里程不低于的概率;
(3)该大学B学院男生与女生人数之比为,B学院体育社团为了解学生参与跑步运动的情况,也按性别进行分层抽样已知A学院和B学院的样本数据整理如下表.
5月份累计跑步里程平均值(单位:)
学院性别 A B
男生 50 59
女生 40 45
设A学院样本中学生5月份累计跑步里程平均值为,B学院样本中学生5月份累计跑步里程平均值为,是否存在,使得 如果存在,求的最大值;如果不存在,说明理由.
21.现有4名男生和3名女生.
(1)若安排这7名学生站成一排照相,要求3名女生互不相邻,这样的排法有多少种?
(2)若邀请这7名学生中的4名参加一项活动,其中男生甲和女生乙不能同时参加,求邀请的方法种数;
(3)若将这7名学生全部安排到5个备选工厂中的4个工厂参加暑期社会实践活动,要求3名女生必须安排在同一个工厂,求这样安排的方法共有多少种?
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】根据空间共线向量的坐标表示建立方程组,解之即可求解.
【详解】由,知,使得,
即,所以,
解得,所以.
故选:B
2.C
【分析】根据给定条件,利用投影向量的意义求解即得.
【详解】由向量,,得,而,
向量在向量上的投影向量.
故选:C
3.A
【分析】建立适当空间站直角坐标系后,借助空间向量表示出的余弦值,结合基本不等式计算即可得解.
【详解】连接交于点,以为坐标原点,建立如图所示的空间直角坐标系,
因为正方形的边长为,所以,
因为,所以为的中点,
设,在直角中,有,故,
所以,
则,
所以,
因为,
当且仅当,即时等号成立,所以的最大值为,
因此的最小值为.
故选:A.
4.C
【分析】首先分析题意,作,建立空间直角坐标系,设出对应点的坐标建立方程,整体代换求解即可.
【详解】作,以A为原点建立如图所示空间直角坐标系,
,
,,
,即
,即C正确,
故选:C.
5.A
【分析】先将5名实习老师按1人、2人、2人分为三组,再安排到3个班中,由排列组合计数求解即可.
【详解】由题意,先将5名实习老师按1人、2人、2人分为三组,再安排到3个班中,
则不同的安排方法有(种).
故选:A.
6.C
【分析】根据题意,由分步计数原理计算“用四种不同得颜色要对如图形中的五部分进行着色”和“任意有公共边的两块着不同颜色”的涂色方法,由古典概型公式计算可得答案.
【详解】根据题意,用四种不同的颜色要对如图形中的五个部分进行着色,每个部分都有4种涂色方法,则有种涂色方法;
若其中任意有公共边的两块着不同颜色,有两种情况:①只用三种颜色涂这5个区域,则有种涂色方法;②用四种颜色涂这5个区域,则有种涂色方法,所以若其中任意有公共边的两块着不同颜色,共有144种涂色方法,故四种不同的颜色要对如图形中的五个部分进行着色,其中任意有公共边的两块着不同颜色的概率为.
故选:C
7.D
【分析】由,写出展开式的通项,即可求出展开式中的常数项.
【详解】因为,
其中展开式的通项为(且),
令,得,∴,
故展开式中的常数项是.
故选:D.
8.B
【分析】利用分步计数原理结合排列组合知识解决.
【详解】事件甲,乙,丙三人不在同一行也不在同一列可分为四步完成,
第一步,从6行中任选三行,共有种方法,
第二步,从所选的三行的15个位置中选一个位置排甲,共有15种方法,
第三步,从余下可选的8个位置中选一个位置排乙,共有8种方法,
第四步,从余下可选的3个位置中选一个位置排丙,共有3种方法,
由分步乘法计数原理可得,
三人不在同一行也不在同一列的不同的站法有种,
故选:B
9.ABD
【分析】由空间向量的数量积运算计算判断A;由数量积的运算律计算判断B;由利用空间向量求出异面直线夹角的余弦判断C;由几何法求出二面角的余弦判断D.
【详解】二面角中,,于,于,,
对于A,,A正确;
对于B,由二面角的大小为,得,
则
,B正确;
对于C,由选项A知,,则与所成的角的余弦为,C错误;
对于D,过作,且使,连接,则四边形是正方形,
有,,而平面,则平面,
又平面,因此,即,由,得,
所以为等边三角形,取中点,连接,则,,
取中点,连接,,有,
又平面,则平面,又平面,则,
因此为二面角的平面角,又,,
显然,即,则,D正确.
故选:ABD
10.BCD
【分析】结合空间直角坐标系的对称关系可判断A,B,C;结合两点间距离公式可求D.
【详解】点关于x轴的对称点的坐标为,故A错误;
点关于xOy平面对称的点的坐标为,故B正确;
关于原点的对称的点的坐标为,故C正确;
两点间的距离为,故D正确.
故选:BCD
11.ACD
【分析】由分步乘法计算可得AC正确;由分类加法和分步乘法计算可得B错误;分丙在第一,第二,第四三种情况用分类加法和分步乘法计算得到D正确.
【详解】A:甲、乙两人之中有一人的成绩为第三人名有种情况,丙的成绩不是第五名有种,剩下全排,所以共有种,故A正确;
B:设甲排在第三,乙可在第一和第五;
当乙在第一时,有种;
当乙在第五时,有种,
甲乙可以互换,所以共有种,故B错误;
C:由条件可知,丙只能在第四,
当甲在第三,乙只能在第一,第二的位置共有种,
由于甲乙可以互换,所以共有种,故C正确;
D:丙在第一时,有种;
丙在第二时,分为两种情况,①甲在第三,有种;②乙在第三,甲在第四或五,有种;
丙在第四,甲只能在第五,此时乙在第三,有2种;
所以共有种,故D正确;
故选:ACD.
12.BC
【分析】根据排列数和组合数的公式及性质逐项判断即可.
【详解】由组合数的性质知,故A错误;
因为,,故,故B正确;
由,得,故C正确;
,故D错误.
故选:BC.
13.①②③
【分析】①可通过线面垂直的判定定理找到点P;②③④都可以通过建立空间直角坐标系解决,其中通过向量的长度可以对②进行判断;利用两条直线所成的角和三角形面积公式可以判断③;求出三个面的法向量,并求出和,即可对④进行判断.
【详解】①因为,在上取点使,
因为,平面,所以平面,
因为平面,所以平面平面,故①正确;
②以为原点,以分别为轴建立空间直角坐标系,如图
,,,,则,,
设,则,,
从而,,所以,故②正确;
③由②,,,
,,
当且仅当时等号成立,所以面积的最小值为,故③正确;
④平面的法向量,平面的法向量,
设平面的法向量,
由即得,
令得,
则,,
令得或,而,故,
从而对存在点P,使得,而不大于直角,
故,故④错误;
故答案为:①②③.
14.
【分析】利用空间向量共线的坐标运算,即可求出结果.
【详解】因为,,
所以,解得,
故答案为:.
15.270
【分析】分选读4部名著或选读5部名著2种情况,根据题意结合组合数分析求解.
【详解】若选读4部名著,则不同的选读名著的方案共有种;
若选读5部名著,可知中国古典名著有2部或3部,则不同的选读名著的方案共有种;
所以不同的选读名著的方案共有种.
故答案为:270.
16.1023
【分析】根据二项式展开式的通项公式,结合题意求得,再通过赋值法先求,再求目标即可.
【详解】的展开式的通项公式为,
令,则可得含项的系数,则,
对,令,解得;对,令,解得,
故.
故答案为:.
17.(1)证明见解析
(2)
【分析】(1)建立空间直角坐标系,求出的坐标,用向量共线定理证明结论.
(2)设,进而用参数求出相应平面的法向量,结合已知二面角大小列方程求参数.
【详解】(1)如图:以为原点,建立空间直角坐标系.
则,,,因为为中点,所以,
,,,因为,所以.
所以,,所以,故.
(2)结合二面角大小知:在线段靠近部分,设(),则,
设,则,即.
所以,.
设平面的法向量为,则
,取.
又平面的法向量可以取.
所以,,.
因为二面角为120°.
所以.
结合图形,,所以.
18.(1)证明见解析
(2)
【分析】(1)设与交于点,根据题意,证得和,结合线面垂直的判定定理,证得平面,进而证得.
(2)由(1)知平面,得到平面,以为坐标原点,建立空间直角坐标系,求得平面和平面的法向量和,结合向量的夹角公式,即可求解.
【详解】(1)证明:如图所示,设与交于点,连接,
因为底面是平行四边形,所以为的中点,
又因为,所以,
因为,且为的中点,所以,
又因为平面,且平面平面,平面平面,
所以平面,
因为平面,所以,
又因为,且平面,所以平面,
因为平面,所以.
(2)解:如图所示,连接,因为为的中位线,所以,
因为平面平面且,
所以,且,
由分别为的中点,看到的,
由(1)知平面,所以平面.
以为坐标原点,以所在直线分别为轴,建立空间直角坐标系,
如图所示,则,
所以,则,
设为平面的法向量,则,
取,可得,所以,
又由平面的一个法向量为,
设平面与平面的夹角为,可得.
即平面与平面的夹角余弦值为.
19.(1)
(2)见解析
【分析】(1)以为原点,建立空间直角坐标系,分别求得平面和平面的一个法向量和,结合向量的夹角公式,即可求解.
(2)设,求出,则,再由可证明直线平面.
【详解】(1)以为坐标原点,建立如图所示的空间直角坐标系,
所以,,
因为,
设平面的法向量为,则,
取,可得,所以,
设平面的法向量为
所以,
所以二面角的大小为.
(2)设,则设,,
所以,所以,
平面的法向量为,
,因为平面,
所以直线平面.
20.(1),概率为
(2)
(3)存在满足条件的,且的最大值为
【分析】(1)先根据男女比即可求出,再根据古典概型即可求出所求概率;
(2)先分别求出在A学院所有男生中任取人,跑步里程不低于的概率及在A学院所有女生中任取人,跑步里程不低于的概率,再根据乘法公式求解即可;
(3)设学院女生人数为,则男生人数为,求出,,即可得到不等式,解得即可.
【详解】(1)依题意,解得,
所以在中的概率为;
(2)学院所抽取的学生中男生有人,
其中5月份的累计跑步里程不低于有人,
女生有人,
其中5月份的累计跑步里程不低于有人,
所以在A学院所有男生中任取人,跑步里程不低于的概率为,
在A学院所有女生中任取人,跑步里程不低于的概率为,
所以4人中恰有2人累计跑步里程不低于的概率为
;
(3)设B学院女生有人,则男生有人,
,
,
依题意,即,
显然,解得,所以的最大值为.
21.(1)1440
(2)25
(3)1200
【分析】(1)采用插空法进行求解即可;
(2)采用去杂法进行求解即可;
(3)根据分类加法计数原理,结合排列和组合的定义进行求解即可.
【详解】(1)由题意可知;运用插空法,可得共有排法数为种.
(2)由题意可知:邀请这7名学生中的4名参加一项活动共有种方法,
男生甲和女生乙同时参加的方法有
共有邀请方法数为种.
(3)有两类不同情形:
①先选4个工厂,将3名女生和1名男生安排在同一个工厂,其余3名男生分别在另三个工厂,一厂安排一人,其方法数为种;
②先选4个工厂,将3名女生安排在一个工厂,4名男生安排在另外三个工厂,有一厂两人,另两厂各一人,
其方法数为种.
所以共有种不同的安排方法.
答案第1页,共2页
答案第1页,共2页
同课章节目录
