数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积与体积 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.3.1棱柱、棱锥、棱台的表面积与体积 课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 21:14:18 | ||
图片预览



文档简介
(共27张PPT)
8.3.1 棱柱、棱锥、棱台的表面积
导
01
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积的求法;
2.会求与棱柱、棱锥、棱台有关的组合体的表面积.
导
01
课堂引入
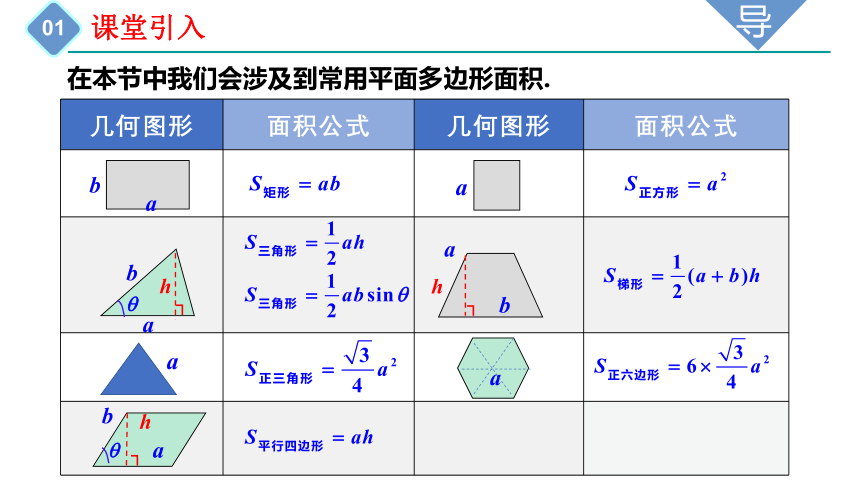
几何图形 面积公式 几何图形 面积公式
┐
┐
┐
在本节中我们会涉及到常用平面多边形面积.
导
01
课堂引入
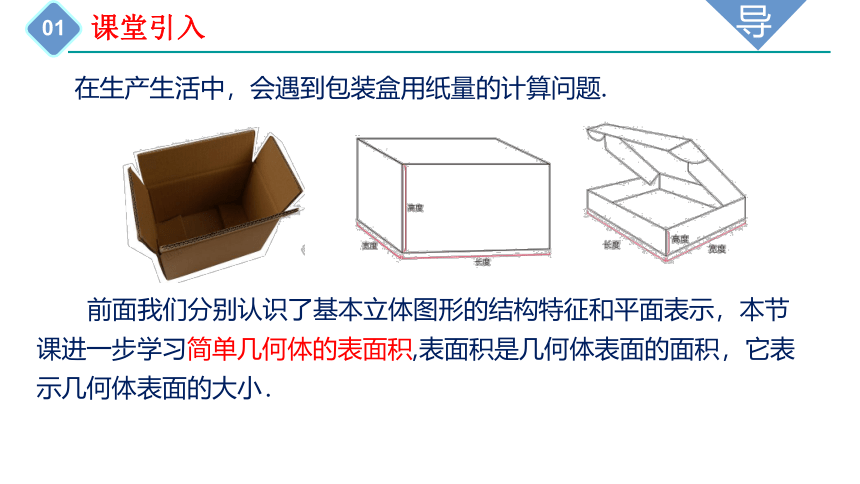
在生产生活中,会遇到包装盒用纸量的计算问题.
前面我们分别认识了基本立体图形的结构特征和平面表示,本节课进一步学习简单几何体的表面积,表面积是几何体表面的面积,它表示几何体表面的大小.
思
02
点拨精讲
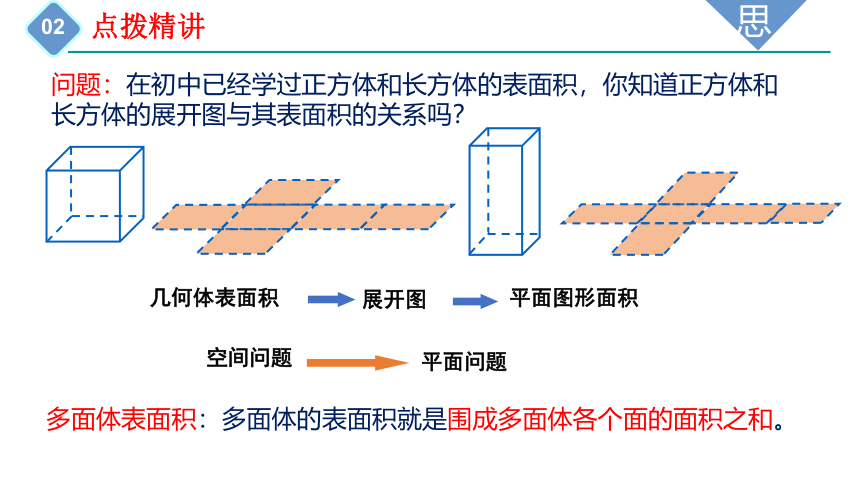
问题:在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
多面体表面积:多面体的表面积就是围成多面体各个面的面积之和。
思
02
点拨精讲
棱台
棱柱
棱锥
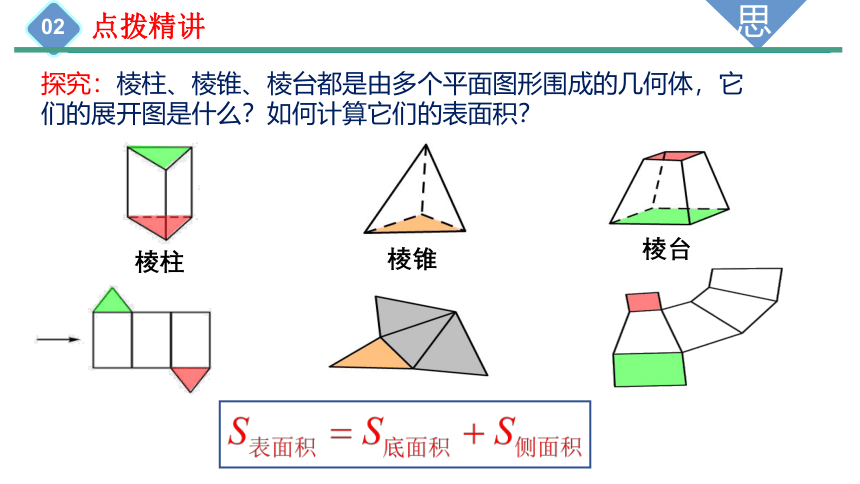
探究:棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
议
03
典例解析
例1 如图示,四面体P-ABC各棱长均为a,求它的表面积.
解:∵ ABC是正三角形,其边长为a.
因此,四面体P-ABC的表面积为
A
C
B
S
议
04
课堂练习
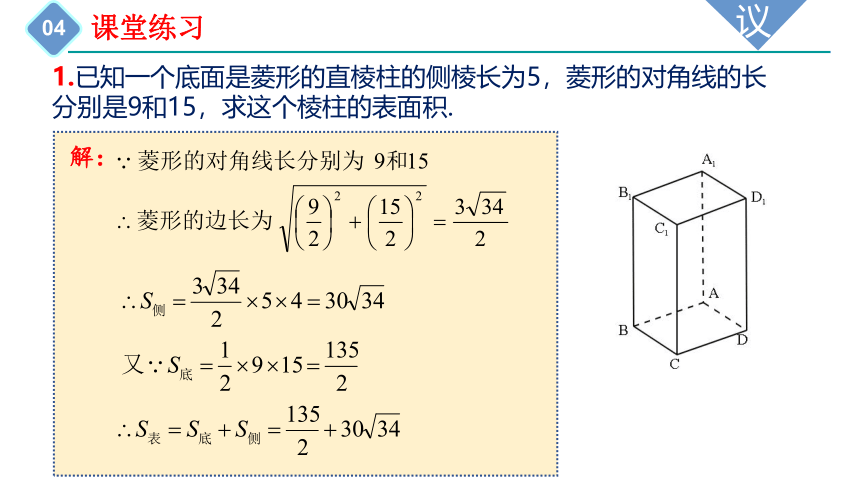
1.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,求这个棱柱的表面积.
解:
议
04
课堂练习
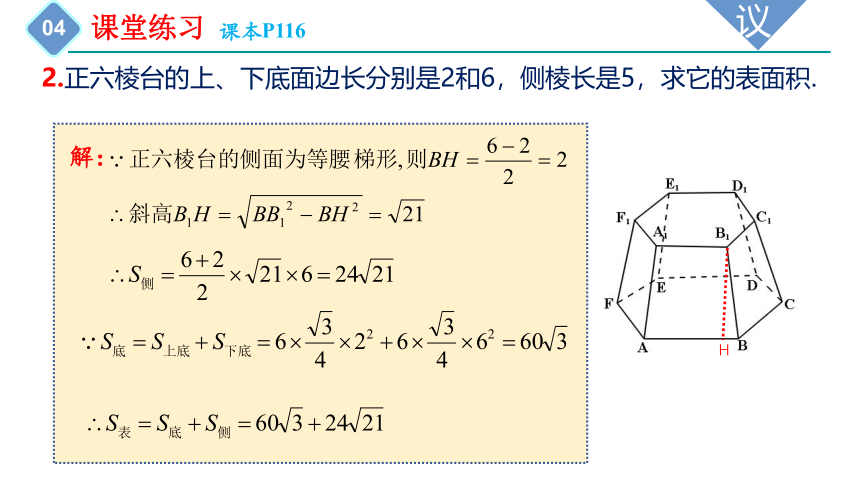
2.正六棱台的上、下底面边长分别是2和6,侧棱长是5,求它的表面积.
解:
H
课本P116
检
07
课堂小结
本节课我们学习了哪些内容?
各面面积之和
展开图
棱柱、棱锥、棱台
棱柱、棱锥、棱台的表面积
课本P116练习4.
练
07
课后练习
8.3.1 棱柱、棱锥、棱台的体积
导
01
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的体积的求法;
2.会求与棱柱、棱锥、棱台有关的组合体的体积.
3.体会祖暅原理与柱体与锥体的体积.
导
01
课堂引入
问题:取一摞书放在桌面上,并改变它们的位置,高度、书中每页纸面积和顺序不变,观察改变前后的体积是否发生变化?
思
02
点拨精讲
我们已经学过的特殊棱柱——正方体、长方体的体积
V正方体=a3
V棱柱=Sh (S,h分别表示长方体的底面积和高)
(a正方体的棱长)
V长方体=abc
(a,b,c分别为长方体长、宽、高)
从棱柱的底和高的角度来看,以上体积公式可以怎样写,由此你能猜想出一般棱柱的体积公式吗
=Sh
=Sh
思
02
点拨精讲
一般地,如果棱柱的底面积是S,高是h.那么这个棱柱的体积:
(1)棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
(2)对直棱柱而言,由于侧棱垂直于底面,因此直棱柱的侧棱长即为直棱柱的高.
重要的是找高
V棱柱=Sh
思
02
点拨精讲
问题:为什么棱锥的体积是棱柱体积的三分之一?
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
C
A’
B’
A
B
A’
C
1
2
3
思
02
点拨精讲
【结论】棱锥的体积等于等底等高的棱柱体积的。
一般地,如果棱锥的底面积是S,高是h,那么该棱锥的体积:
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
思
02
点拨精讲
问题: 棱台根据棱台的定义,它的体积应该怎样求呢?
(S′, S, h分别是棱台的上下底面积和高)
思
02
点拨精讲
问题:棱柱、棱锥、棱台的体积公式之间有什么关系?你用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
几何体 棱柱 棱台 棱锥
直 观 图
体 积
上底面扩大到与下底面全等
上底面缩小为一个点
S′=S
S′=0
议
03
典例解析
例1.如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米
解:
A'
B'
C'
D'
A
B
C
D
P
如图示,由题意知
∴这个漏斗的容积为
议
04
课堂练习
解:∵O为 ABC的中心
因此,正三棱锥P-ABC的体积为
1. 正三棱锥P-ABC的底面边长为2,侧棱长为3,.求正三棱锥的体积.
P
A
B
C
O
E
议
04
课堂练习
解:
2.正四棱台的底面边长分别为20 cm和10 cm,侧面面积为780 cm2,求其体积.
∵S侧=4××(10+20)×EE1=780(cm2),
∴EE1=13 cm.
在直角梯形EOO1E1中,O1E1=A1B1=5 cm,
OE=AB=10 cm,
∴O1O==12(cm),
∴该正四棱台的体积为
V=×(102+202+10×20)×12=2 800(cm3).
议
04
课堂练习
解:设长方体的棱长为a,b,c
因此棱锥的体积与剩下的几何体体积的比为
3. 如图,将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比.
课本P119
检
05
课堂小结
本节课我们学习了哪些内容?
1. 求几何体体积的常用方法
思
06
探究与发现
祖暅原理:幂势既同,则积不容异。
祖暅
中国南北朝时期算学家、天文学家,祖冲之之子。他运用祖暅原理和由他创造的开立圆术,发展了他父亲的研究成果,巧妙地证得球的体积公式。他求得这一公式比意大利数学家卡瓦列利(Bonaventura Cavalieri,1589年—1647年)至少要早1100年。
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
课本P116练习3
课本P120习题4.
练
07
课后练习
8.3.1 棱柱、棱锥、棱台的表面积
导
01
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积的求法;
2.会求与棱柱、棱锥、棱台有关的组合体的表面积.
导
01
课堂引入
几何图形 面积公式 几何图形 面积公式
┐
┐
┐
在本节中我们会涉及到常用平面多边形面积.
导
01
课堂引入
在生产生活中,会遇到包装盒用纸量的计算问题.
前面我们分别认识了基本立体图形的结构特征和平面表示,本节课进一步学习简单几何体的表面积,表面积是几何体表面的面积,它表示几何体表面的大小.
思
02
点拨精讲
问题:在初中已经学过正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
展开图
平面图形面积
空间问题
平面问题
多面体表面积:多面体的表面积就是围成多面体各个面的面积之和。
思
02
点拨精讲
棱台
棱柱
棱锥
探究:棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
议
03
典例解析
例1 如图示,四面体P-ABC各棱长均为a,求它的表面积.
解:∵ ABC是正三角形,其边长为a.
因此,四面体P-ABC的表面积为
A
C
B
S
议
04
课堂练习
1.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,求这个棱柱的表面积.
解:
议
04
课堂练习
2.正六棱台的上、下底面边长分别是2和6,侧棱长是5,求它的表面积.
解:
H
课本P116
检
07
课堂小结
本节课我们学习了哪些内容?
各面面积之和
展开图
棱柱、棱锥、棱台
棱柱、棱锥、棱台的表面积
课本P116练习4.
练
07
课后练习
8.3.1 棱柱、棱锥、棱台的体积
导
01
学习目标
1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的体积的求法;
2.会求与棱柱、棱锥、棱台有关的组合体的体积.
3.体会祖暅原理与柱体与锥体的体积.
导
01
课堂引入
问题:取一摞书放在桌面上,并改变它们的位置,高度、书中每页纸面积和顺序不变,观察改变前后的体积是否发生变化?
思
02
点拨精讲
我们已经学过的特殊棱柱——正方体、长方体的体积
V正方体=a3
V棱柱=Sh (S,h分别表示长方体的底面积和高)
(a正方体的棱长)
V长方体=abc
(a,b,c分别为长方体长、宽、高)
从棱柱的底和高的角度来看,以上体积公式可以怎样写,由此你能猜想出一般棱柱的体积公式吗
=Sh
=Sh
思
02
点拨精讲
一般地,如果棱柱的底面积是S,高是h.那么这个棱柱的体积:
(1)棱柱的高是指两底面之间的距离,即从一底面上任意一点向另一个底面作垂线,这点与垂足(垂线与底面的交点)之间的距离.
(2)对直棱柱而言,由于侧棱垂直于底面,因此直棱柱的侧棱长即为直棱柱的高.
重要的是找高
V棱柱=Sh
思
02
点拨精讲
问题:为什么棱锥的体积是棱柱体积的三分之一?
A
B
C
A’
B’
C’
A
B
C
A’
B’
C’
C
A’
B’
A
B
A’
C
1
2
3
思
02
点拨精讲
【结论】棱锥的体积等于等底等高的棱柱体积的。
一般地,如果棱锥的底面积是S,高是h,那么该棱锥的体积:
棱锥的高是指从顶点向底面作垂线,顶点与垂足之间的距离.
思
02
点拨精讲
问题: 棱台根据棱台的定义,它的体积应该怎样求呢?
(S′, S, h分别是棱台的上下底面积和高)
思
02
点拨精讲
问题:棱柱、棱锥、棱台的体积公式之间有什么关系?你用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
几何体 棱柱 棱台 棱锥
直 观 图
体 积
上底面扩大到与下底面全等
上底面缩小为一个点
S′=S
S′=0
议
03
典例解析
例1.如右图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m,公共面ABCD是边长为1m的正方形,那么这个漏斗的容积是多少立方米
解:
A'
B'
C'
D'
A
B
C
D
P
如图示,由题意知
∴这个漏斗的容积为
议
04
课堂练习
解:∵O为 ABC的中心
因此,正三棱锥P-ABC的体积为
1. 正三棱锥P-ABC的底面边长为2,侧棱长为3,.求正三棱锥的体积.
P
A
B
C
O
E
议
04
课堂练习
解:
2.正四棱台的底面边长分别为20 cm和10 cm,侧面面积为780 cm2,求其体积.
∵S侧=4××(10+20)×EE1=780(cm2),
∴EE1=13 cm.
在直角梯形EOO1E1中,O1E1=A1B1=5 cm,
OE=AB=10 cm,
∴O1O==12(cm),
∴该正四棱台的体积为
V=×(102+202+10×20)×12=2 800(cm3).
议
04
课堂练习
解:设长方体的棱长为a,b,c
因此棱锥的体积与剩下的几何体体积的比为
3. 如图,将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比.
课本P119
检
05
课堂小结
本节课我们学习了哪些内容?
1. 求几何体体积的常用方法
思
06
探究与发现
祖暅原理:幂势既同,则积不容异。
祖暅
中国南北朝时期算学家、天文学家,祖冲之之子。他运用祖暅原理和由他创造的开立圆术,发展了他父亲的研究成果,巧妙地证得球的体积公式。他求得这一公式比意大利数学家卡瓦列利(Bonaventura Cavalieri,1589年—1647年)至少要早1100年。
夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
课本P116练习3
课本P120习题4.
练
07
课后练习
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
