导数(浙江省台州市路桥区)
图片预览









文档简介
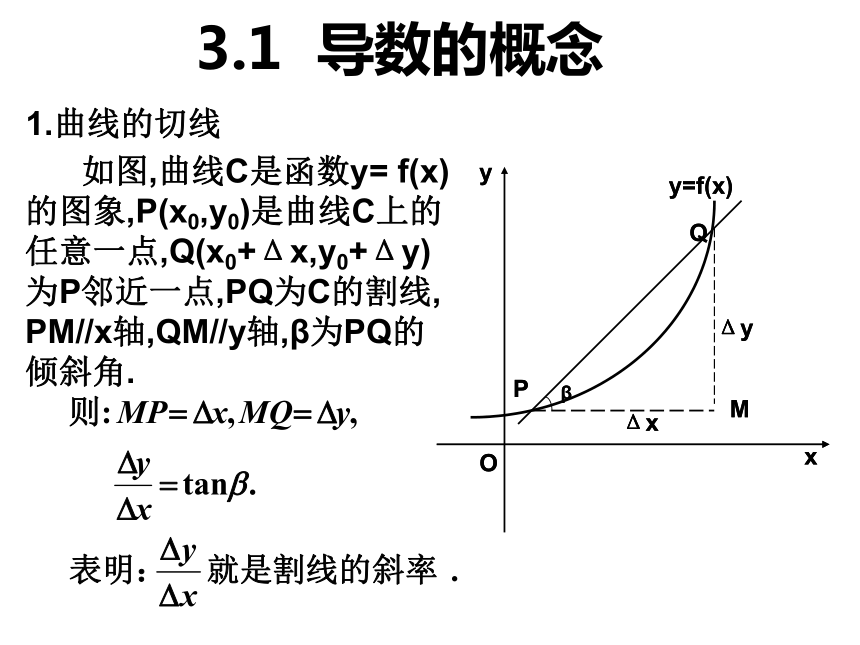
课件31张PPT。导数的概念3.1 导数的概念 1.曲线的切线 如图,曲线C是函数y= f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.PQ割线切线T 请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即: 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限. 注意,曲线在某点处的切线:
(1)与该点的位置有关;
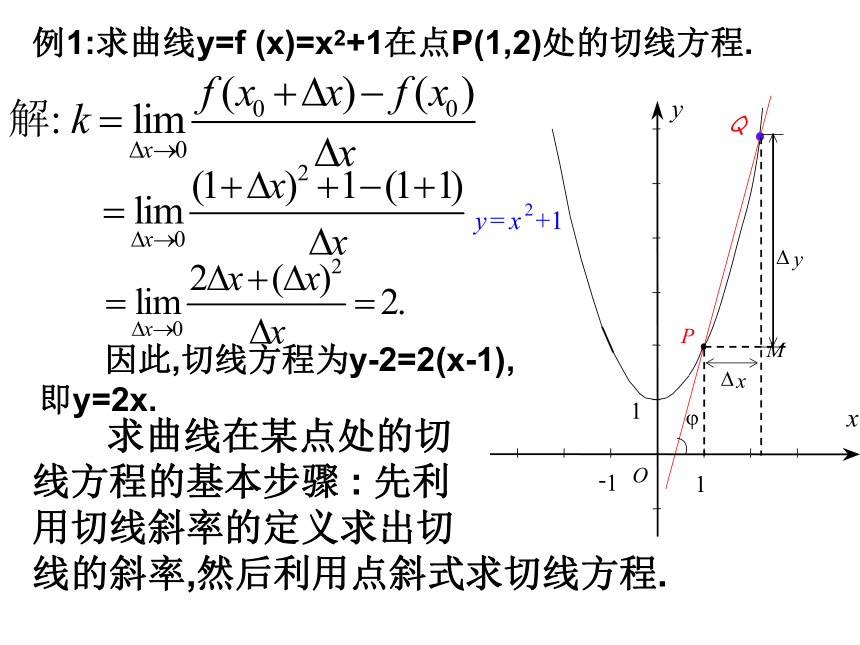
(2)要根据割线是否有极限位置来判断与求解切线。 因此,切线方程为y-2=2(x-1),
即y=2x. 求曲线在某点处的切
线方程的基本步骤 : 先利
用切线斜率的定义求出切
线的斜率,然后利用点斜式求切线方程.练习:求曲线 上一点P(1,-1)处的切线方程.答案:y=3x-4.2.瞬时速度 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t表示时间),求物体在t0时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Δt 的位置是s(t0+ Δ t)=OA1,则从t0 到 t0 +Δt 这段时间内,物体的位移是:在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也既需要通过瞬时速度来反映. 如果物体的运动规律是 s=s(t),那么物体在时刻t的瞬时速度v,就是物体在t到 t+Δt这段时间内,当 Δt?0 时平均速度:例2:物体作自由落体运动,运动方程为: 其中位 移单位是m,时间单位是s, g=10m/s2.求:
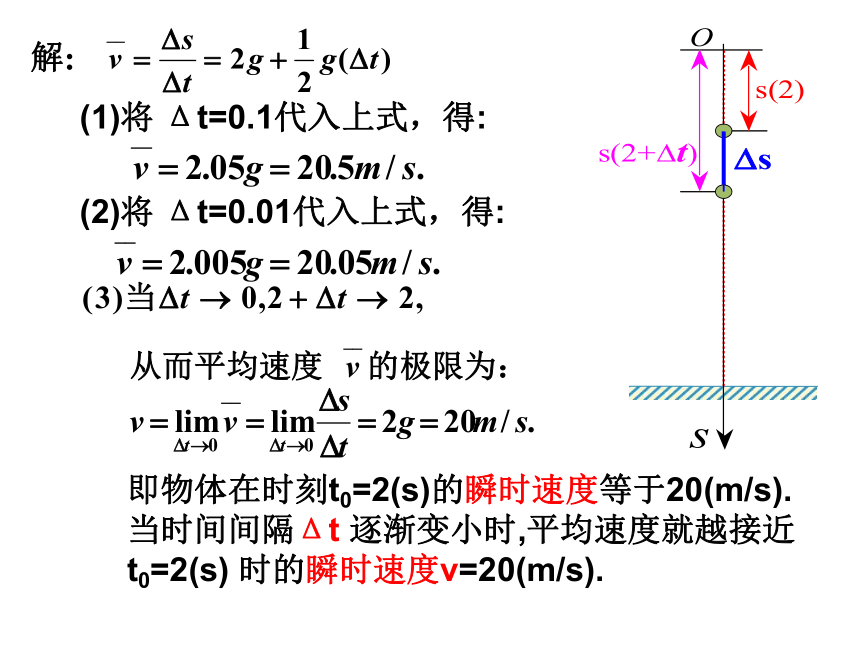
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度. 解:(1)将 Δt=0.1代入上式,得: (2)将 Δt=0.01代入上式,得: 即物体在时刻t0=2(s)的瞬时速度等于20(m/s).
当时间间隔Δt 逐渐变小时,平均速度就越接近t0=2(s) 时的瞬时速度v=20(m/s).练习:某质点沿直线运动,运动规律是s=5t2+6,求:
(1)2≤t≤2+Δt这段时间内的平均速度,这里Δt取值
范围为1;
(2)t=2时刻的瞬时速度.3.导数的概念 从上面两个实例,一个是曲线的切线的斜率,一个是瞬时速度,具体意义不同,但通过比较可以看出它们的数
学表达式结构是一样的,即计算极限 ,这就是我们要学习的导数的定义. 定义:设函数y=f (x)在点x0处及其附近有定义,当自变量x在点x0处有改变量Δx时函数有相应的改变量Δy=f(x0+ Δx)- f(x0).如果当Δx?0 时,Δy/Δx的极限存在,这个极限就叫做函数f (x)在点x0处的导数(或变化率)记作 即:
如瞬时速度就是位移函数s (t)对时间t的导数. 是函数f (x)在以x0与x0+Δx
为端点的区间[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f (x)在点x0 处的变化率,它反映了函数随自变量变化而变化的快慢程度. 如果函数y=f (x)在点x=x0存在导数,就说函数y= f (x)在点x0处可导,如果极限不存在,就说函数 f (x)在点x0处不可导. 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:例1:(1)求函数y=x2在x=1处的导数;
(2)求函数y=x+1/x在x=2处的导数.作业:
P114 习题3.1 1, 2, 6, 7 如果函数y=f (x)在区间(a ,b)内每一点都可导,就说函数y=f (x)在区间(a ,b)内可导.这时,对每一个x? (a ,b)都有唯一确定的导数值与它对应,这样在区间(a,b)内就构成一个新的函数.这个新的函数叫做函数f (x)在区间(a ,b)内的导函数,记作 ,即:在不致发生混淆时,导函数也简称导数. 如果函数y=f(x)在点x0处可导,那么函数在点x0处连续.求函数y=f(x)的导数可分如下三步:4.导数的几何意义 函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率,即曲线y=
f(x)在点P(x0 ,f(x0)) 处的切线的斜率是 . 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:例1:设f(x)为可导函数,且满足条件 ,
求曲线y=f(x)在点(1,f(1))处的切线的斜率.故所求的斜率为-2.例2:如图,已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.例1:判断下列各命题的真假:
(1)已知函数y=f (x)的图象上的点列P1,P2,P3,…Pn…,
则过P0与Pn两点的直线的
斜率就是函数在点P0处的导数.答:由函数在点P0处的导数的几何意义知:函数在点
P0处的导数是过P0点曲线(即函数y=f (x)的图象)
的切线的斜率,而不是割线P0Pn的斜率,故它是一
个假命题.(2)若物体的运动规律是S=f (t),则物体在时刻t0的瞬
时速度V等于答:由于它完全符合瞬时速度的定义,故它是一个真
命题.(3)若函数y=f(x)的定义域为A,则对任一 只要
函数在x0处连续,则 就必存在.5.例题选讲答:它是一个假命题.例如,函数 在x=0处连续,但
它在x=0处的导数不存在.(4)设
是函数y=f(x)的图象上的三点,且函数在P1,P2,P3
三点处的导数均存在.若 ,则必有答: ,由于f (x)的导函
数 未必是单调增函数.因此,
不一定成立,例如f (x)=x3,则 显然有
故是假命题.说明:要正确判断命题的真假,需真正理解:曲线在点P处
切线的斜率、瞬时速度、连续与可导等概念,还要
把握好要确定一个命题为真命题,则需给出论证,
而要给出否定的结论,举一个反例就足够了.例2:设函数f (x)在点x0处可导,求下列各极限值:分析:利用函数f (x)在点x0处可导的条件,将题目中给定
的极限恒等变形为导数定义的形式.注意在导数定
义中,自变量的增量Δx的形式是多样的,但不论Δx
选择哪种形式, Δy也必须选择与之相对应的形式.例3:证明:(1)可导的偶函数的导函数为奇函数;
(2)可导的奇函数的导函数为偶函数.证:(1)设偶函数f (x),则有f (-x)=f (x).(2)仿(1)可证命题成立,在此略去,供同学们在课后练
习用.练习1:设函数f (x)在点x0处可导,求下列各极限值:练习2:设函数f (x)在点x=a处可导,试用a、f(a)和例4:判断函数y=|3x-1|在x=1/3处是否可导.从而函数y=|3x-1|在x=1/3处不可导.注:这是一个函数在某点连续但不可导的例子.练习3:函数f (x)=|x|(1+x)在点x0=0处是否有导数?若有,
求出来,若没有,说明理由.故函数f(x)=|x|(1+x)在点x0=0处没有导数,即不可导.6.小结a.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态。 b.要切实掌握求导数的三个步骤:(1)求函数的增
量;(2)求平均变化率;(3)取极限,得导数。c.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数”
之间的区别与联系。(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数。(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 。(3)如果函数y=f (x)在开区间(a ,b)内每一点都可导, 就说函数y=f (x)在开区间(a ,b)内可导,这时,对于开区间内每一个确定的值x0,都对应着一个确定的导数 ,这样就在开区间(a ,b)内 可构成一个新的函数,称作f (x)的导函数。 (4)函数f (x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 。这也是
求函数在点x0处的导数的方法之一。 d.函数f (x)在点x0处有导数,则在该点处函数f (x)的曲线必有切线,且导数值是该切线的斜率;但函数f (x)
的曲线在点x0处有切线,而函数f (x)在该点处不一定
可导。如函数 在x=0处有切线,但不可导。e.求切线方程的步骤:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即 f.无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想,丢掉极限思想就无法理解导数概念。
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.PQ割线切线T 请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即: 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限. 注意,曲线在某点处的切线:
(1)与该点的位置有关;
(2)要根据割线是否有极限位置来判断与求解切线。 因此,切线方程为y-2=2(x-1),
即y=2x. 求曲线在某点处的切
线方程的基本步骤 : 先利
用切线斜率的定义求出切
线的斜率,然后利用点斜式求切线方程.练习:求曲线 上一点P(1,-1)处的切线方程.答案:y=3x-4.2.瞬时速度 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t表示时间),求物体在t0时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Δt 的位置是s(t0+ Δ t)=OA1,则从t0 到 t0 +Δt 这段时间内,物体的位移是:在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也既需要通过瞬时速度来反映. 如果物体的运动规律是 s=s(t),那么物体在时刻t的瞬时速度v,就是物体在t到 t+Δt这段时间内,当 Δt?0 时平均速度:例2:物体作自由落体运动,运动方程为: 其中位 移单位是m,时间单位是s, g=10m/s2.求:
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度. 解:(1)将 Δt=0.1代入上式,得: (2)将 Δt=0.01代入上式,得: 即物体在时刻t0=2(s)的瞬时速度等于20(m/s).
当时间间隔Δt 逐渐变小时,平均速度就越接近t0=2(s) 时的瞬时速度v=20(m/s).练习:某质点沿直线运动,运动规律是s=5t2+6,求:
(1)2≤t≤2+Δt这段时间内的平均速度,这里Δt取值
范围为1;
(2)t=2时刻的瞬时速度.3.导数的概念 从上面两个实例,一个是曲线的切线的斜率,一个是瞬时速度,具体意义不同,但通过比较可以看出它们的数
学表达式结构是一样的,即计算极限 ,这就是我们要学习的导数的定义. 定义:设函数y=f (x)在点x0处及其附近有定义,当自变量x在点x0处有改变量Δx时函数有相应的改变量Δy=f(x0+ Δx)- f(x0).如果当Δx?0 时,Δy/Δx的极限存在,这个极限就叫做函数f (x)在点x0处的导数(或变化率)记作 即:
如瞬时速度就是位移函数s (t)对时间t的导数. 是函数f (x)在以x0与x0+Δx
为端点的区间[x0,x0+Δx](或[x0+Δx,x0])上的平均变化率,而导数则是函数f (x)在点x0 处的变化率,它反映了函数随自变量变化而变化的快慢程度. 如果函数y=f (x)在点x=x0存在导数,就说函数y= f (x)在点x0处可导,如果极限不存在,就说函数 f (x)在点x0处不可导. 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:例1:(1)求函数y=x2在x=1处的导数;
(2)求函数y=x+1/x在x=2处的导数.作业:
P114 习题3.1 1, 2, 6, 7 如果函数y=f (x)在区间(a ,b)内每一点都可导,就说函数y=f (x)在区间(a ,b)内可导.这时,对每一个x? (a ,b)都有唯一确定的导数值与它对应,这样在区间(a,b)内就构成一个新的函数.这个新的函数叫做函数f (x)在区间(a ,b)内的导函数,记作 ,即:在不致发生混淆时,导函数也简称导数. 如果函数y=f(x)在点x0处可导,那么函数在点x0处连续.求函数y=f(x)的导数可分如下三步:4.导数的几何意义 函数 y=f(x)在点x0处的导数的几何意义,就是曲线 y=f(x)在点P(x0 ,f(x0))处的切线的斜率,即曲线y=
f(x)在点P(x0 ,f(x0)) 处的切线的斜率是 . 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:例1:设f(x)为可导函数,且满足条件 ,
求曲线y=f(x)在点(1,f(1))处的切线的斜率.故所求的斜率为-2.例2:如图,已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.例1:判断下列各命题的真假:
(1)已知函数y=f (x)的图象上的点列P1,P2,P3,…Pn…,
则过P0与Pn两点的直线的
斜率就是函数在点P0处的导数.答:由函数在点P0处的导数的几何意义知:函数在点
P0处的导数是过P0点曲线(即函数y=f (x)的图象)
的切线的斜率,而不是割线P0Pn的斜率,故它是一
个假命题.(2)若物体的运动规律是S=f (t),则物体在时刻t0的瞬
时速度V等于答:由于它完全符合瞬时速度的定义,故它是一个真
命题.(3)若函数y=f(x)的定义域为A,则对任一 只要
函数在x0处连续,则 就必存在.5.例题选讲答:它是一个假命题.例如,函数 在x=0处连续,但
它在x=0处的导数不存在.(4)设
是函数y=f(x)的图象上的三点,且函数在P1,P2,P3
三点处的导数均存在.若 ,则必有答: ,由于f (x)的导函
数 未必是单调增函数.因此,
不一定成立,例如f (x)=x3,则 显然有
故是假命题.说明:要正确判断命题的真假,需真正理解:曲线在点P处
切线的斜率、瞬时速度、连续与可导等概念,还要
把握好要确定一个命题为真命题,则需给出论证,
而要给出否定的结论,举一个反例就足够了.例2:设函数f (x)在点x0处可导,求下列各极限值:分析:利用函数f (x)在点x0处可导的条件,将题目中给定
的极限恒等变形为导数定义的形式.注意在导数定
义中,自变量的增量Δx的形式是多样的,但不论Δx
选择哪种形式, Δy也必须选择与之相对应的形式.例3:证明:(1)可导的偶函数的导函数为奇函数;
(2)可导的奇函数的导函数为偶函数.证:(1)设偶函数f (x),则有f (-x)=f (x).(2)仿(1)可证命题成立,在此略去,供同学们在课后练
习用.练习1:设函数f (x)在点x0处可导,求下列各极限值:练习2:设函数f (x)在点x=a处可导,试用a、f(a)和例4:判断函数y=|3x-1|在x=1/3处是否可导.从而函数y=|3x-1|在x=1/3处不可导.注:这是一个函数在某点连续但不可导的例子.练习3:函数f (x)=|x|(1+x)在点x0=0处是否有导数?若有,
求出来,若没有,说明理由.故函数f(x)=|x|(1+x)在点x0=0处没有导数,即不可导.6.小结a.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态。 b.要切实掌握求导数的三个步骤:(1)求函数的增
量;(2)求平均变化率;(3)取极限,得导数。c.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数”
之间的区别与联系。(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数。(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 。(3)如果函数y=f (x)在开区间(a ,b)内每一点都可导, 就说函数y=f (x)在开区间(a ,b)内可导,这时,对于开区间内每一个确定的值x0,都对应着一个确定的导数 ,这样就在开区间(a ,b)内 可构成一个新的函数,称作f (x)的导函数。 (4)函数f (x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 。这也是
求函数在点x0处的导数的方法之一。 d.函数f (x)在点x0处有导数,则在该点处函数f (x)的曲线必有切线,且导数值是该切线的斜率;但函数f (x)
的曲线在点x0处有切线,而函数f (x)在该点处不一定
可导。如函数 在x=0处有切线,但不可导。e.求切线方程的步骤:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即 f.无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想,丢掉极限思想就无法理解导数概念。
