导数的应用(浙江省台州市路桥区)
文档属性
| 名称 | 导数的应用(浙江省台州市路桥区) |  | |
| 格式 | rar | ||
| 文件大小 | 144.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-17 21:17:00 | ||
图片预览



文档简介
课件19张PPT。3.3.2极大值与极小值知 识 回 顾1、一般地,设函数y=f(x)在某个区间
内可导,则函数在该区间
如果f′(x)>0, 如果f′(x)<0, 则f(x)为增函数;则f(x)为减函数. 2、用导数法确定函数的单调性时的步骤是:
(1)(3)求出函数的导函数(2)求解不等式f′(x)>0,求得其解集,再根据解集写出单调递增区间求解不等式f′(x)<0,求得其解集,
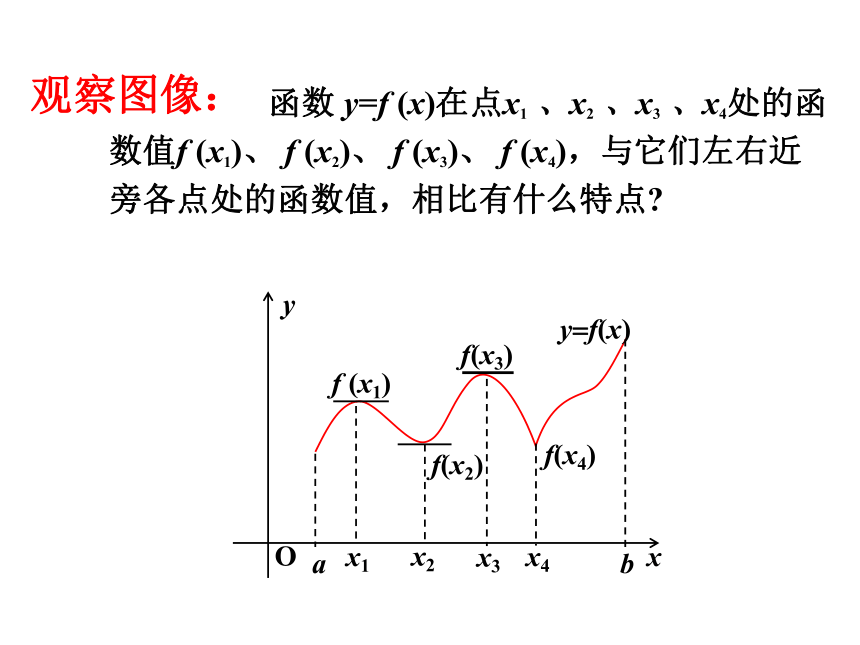
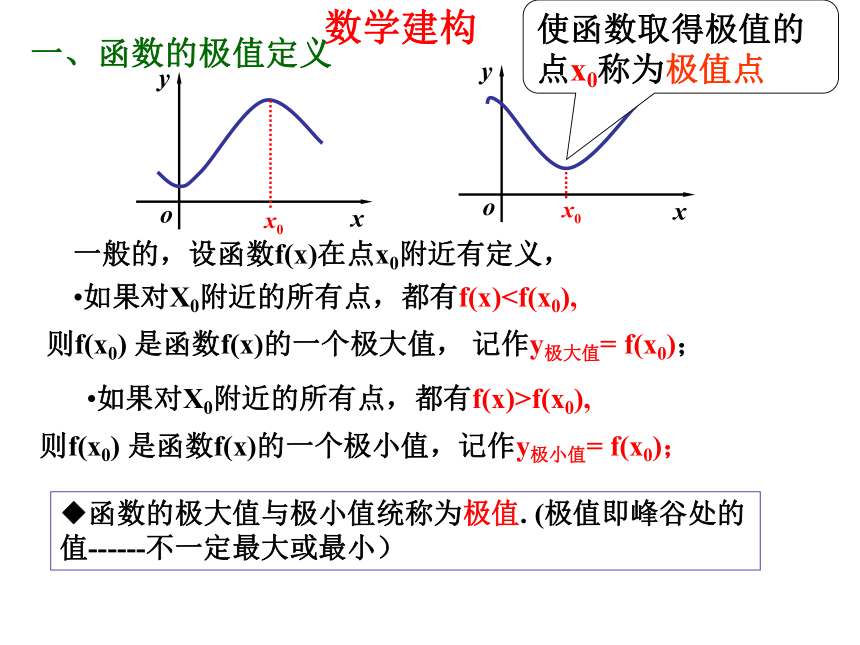
再根据解集写出单调递减区间求函数的定义域 函数 y=f (x)在点x1 、x2 、x3 、x4处的函数值f (x1)、 f (x2)、 f (x3)、 f (x4),与它们左右近旁各点处的函数值,相比有什么特点?观察图像:一、函数的极值定义一般的,设函数f(x)在点x0附近有定义,如果对X0附近的所有点,都有f(x)f(x0), 则f(x0) 是函数f(x)的一个极小值,记作y极小值= f(x0);◆函数的极大值与极小值统称为极值. (极值即峰谷处的值------不一定最大或最小)使函数取得极值的点x0称为极值点数学建构 (3)极大值与极小值没有必然关系,
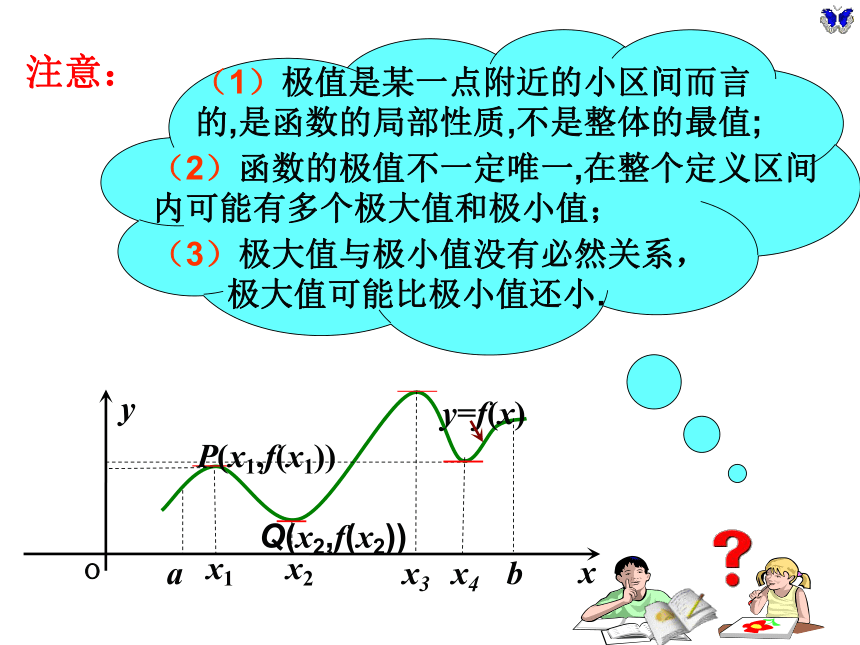
极大值可能比极小值还小. 注意:(1)极值是某一点附近的小区间而言
的,是函数的局部性质,不是整体的最值;(2)函数的极值不一定唯一,在整个定义区间
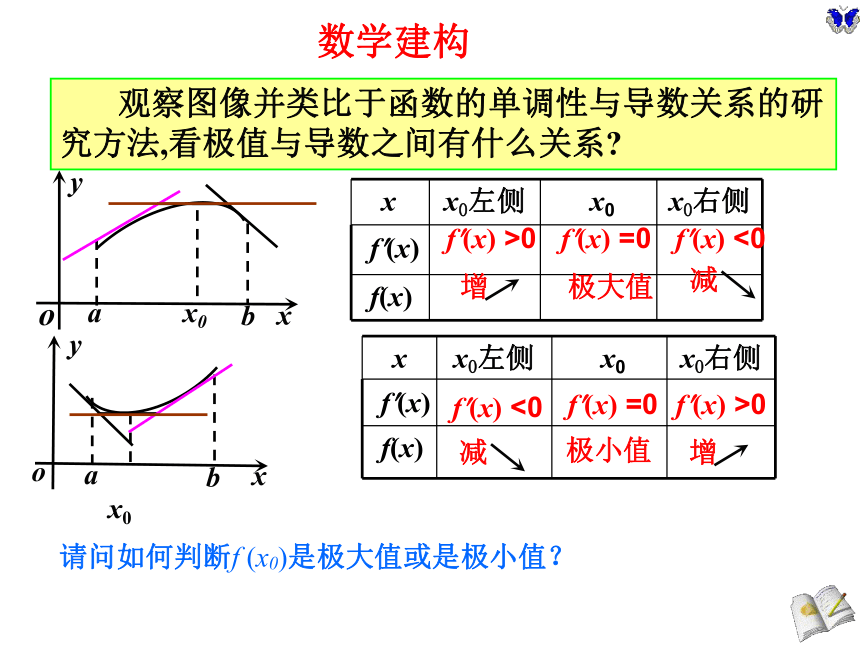
内可能有多个极大值和极小值; 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?f?(x) >0f?(x) =0f?(x) <0极大值f?(x) <0f?(x) =0极小值f?(x) >0数学建构请问如何判断f (x0)是极大值或是极小值? f ?(x)<0x1在极大值点附近在极小值点附近 f ?(x)<0 f ?(x)>0 f ?(x)>0二、判断函数极值的方法x2左正右负为极大,右正左负为极小观察与思考:极值与导数有何关系?在极值点处,曲线如果有切线,则切线是水平的。例1 求函数 的极值。解:定义域为R,y′=x2-4由y′=0可得x=-2或 x=2当x变化时,y′, y的变化情况如下表:因此,当x=-2时, y极大值=17/3 当x=2时, y极小值=-5++0-0极大值
17/3极小值
-5求可导函数f(x)极值的 步骤:(2)求导数f ’(x);(3)求方程f ’(x)=0的根; (4)把定义域划分为部分区间,并列成表格检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值;如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;(1) 确定函数的定义域;例2 求函数 y=(x2-1)3+1 的极值。解:定义域为R, y′=6x(x2-1)2。由y′=0可得x1=-1, x2=0 ,x3=1当x变化时,y′ , y的变化情况如下表:因此,当x=0时, y极小值=0点评:一点是极值点的充分条件是这点两侧的导数异号。1.求f(x)=x2-x-2的极值.解:练习:练习2:求函数 的极值.解:令 =0,解得x1=-1,x2=1.当x变化时, ,y的变化情况如下表:因此,当x=-1时有极大值,并且,y极大值=3;
而,当x=1时有极小值,并且,y极小值=- 3.3:下列函数中,x=0是极值点的函数
是( )
A.y=-x3 B.y=x2
C.y=x2-x D.y=1/x分析:做这题需要按求极值的三个步骤,一个一个求出来吗?不需要,因为它只要判断x=0是否是极值点,只要看x=0点两侧的导数是否异号就可以了。B4、函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习:A注意:数形结合以及原函数与导函数图像的区别5、 函数 在 时有极值10,则a,b的值为( )
A、 或
B、 或
C、 D、 以上都不对 C,注意:f/(x0)=0是函数取得极值的必要不充分条件注意代入检验 6、故当x=-a时,f(x)有极大值f(-a)=-2a;当x=a时,f(x)有极小值f(a)=2a.作业:求函数 的极值.解:函数的定义域为令 ,解得x1=-a,x2=a(a>0).当x变化时, ,f(x)的变化情况如下表:
内可导,则函数在该区间
如果f′(x)>0, 如果f′(x)<0, 则f(x)为增函数;则f(x)为减函数. 2、用导数法确定函数的单调性时的步骤是:
(1)(3)求出函数的导函数(2)求解不等式f′(x)>0,求得其解集,再根据解集写出单调递增区间求解不等式f′(x)<0,求得其解集,
再根据解集写出单调递减区间求函数的定义域 函数 y=f (x)在点x1 、x2 、x3 、x4处的函数值f (x1)、 f (x2)、 f (x3)、 f (x4),与它们左右近旁各点处的函数值,相比有什么特点?观察图像:一、函数的极值定义一般的,设函数f(x)在点x0附近有定义,如果对X0附近的所有点,都有f(x)
极大值可能比极小值还小. 注意:(1)极值是某一点附近的小区间而言
的,是函数的局部性质,不是整体的最值;(2)函数的极值不一定唯一,在整个定义区间
内可能有多个极大值和极小值; 观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?f?(x) >0f?(x) =0f?(x) <0极大值f?(x) <0f?(x) =0极小值f?(x) >0数学建构请问如何判断f (x0)是极大值或是极小值? f ?(x)<0x1在极大值点附近在极小值点附近 f ?(x)<0 f ?(x)>0 f ?(x)>0二、判断函数极值的方法x2左正右负为极大,右正左负为极小观察与思考:极值与导数有何关系?在极值点处,曲线如果有切线,则切线是水平的。例1 求函数 的极值。解:定义域为R,y′=x2-4由y′=0可得x=-2或 x=2当x变化时,y′, y的变化情况如下表:因此,当x=-2时, y极大值=17/3 当x=2时, y极小值=-5++0-0极大值
17/3极小值
-5求可导函数f(x)极值的 步骤:(2)求导数f ’(x);(3)求方程f ’(x)=0的根; (4)把定义域划分为部分区间,并列成表格检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值;如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;(1) 确定函数的定义域;例2 求函数 y=(x2-1)3+1 的极值。解:定义域为R, y′=6x(x2-1)2。由y′=0可得x1=-1, x2=0 ,x3=1当x变化时,y′ , y的变化情况如下表:因此,当x=0时, y极小值=0点评:一点是极值点的充分条件是这点两侧的导数异号。1.求f(x)=x2-x-2的极值.解:练习:练习2:求函数 的极值.解:令 =0,解得x1=-1,x2=1.当x变化时, ,y的变化情况如下表:因此,当x=-1时有极大值,并且,y极大值=3;
而,当x=1时有极小值,并且,y极小值=- 3.3:下列函数中,x=0是极值点的函数
是( )
A.y=-x3 B.y=x2
C.y=x2-x D.y=1/x分析:做这题需要按求极值的三个步骤,一个一个求出来吗?不需要,因为它只要判断x=0是否是极值点,只要看x=0点两侧的导数是否异号就可以了。B4、函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习:A注意:数形结合以及原函数与导函数图像的区别5、 函数 在 时有极值10,则a,b的值为( )
A、 或
B、 或
C、 D、 以上都不对 C,注意:f/(x0)=0是函数取得极值的必要不充分条件注意代入检验 6、故当x=-a时,f(x)有极大值f(-a)=-2a;当x=a时,f(x)有极小值f(a)=2a.作业:求函数 的极值.解:函数的定义域为令 ,解得x1=-a,x2=a(a>0).当x变化时, ,f(x)的变化情况如下表:
