江苏省徐州市睢宁县宁海外国语学校苏科版九年级数学下册第七章 锐角三角函数小结与思考课件(共16张PPT)
文档属性
| 名称 | 江苏省徐州市睢宁县宁海外国语学校苏科版九年级数学下册第七章 锐角三角函数小结与思考课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 387.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-23 16:27:42 | ||
图片预览



文档简介
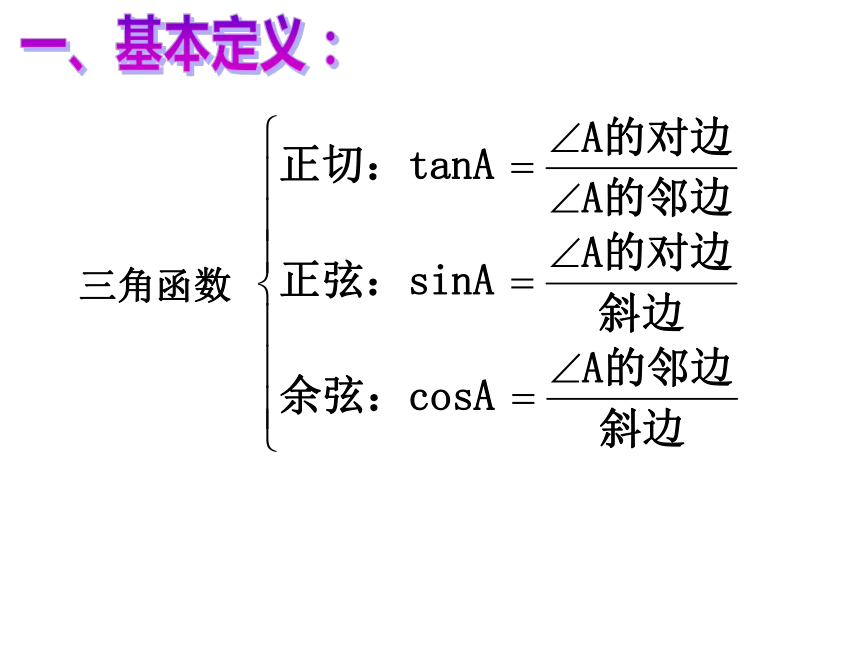
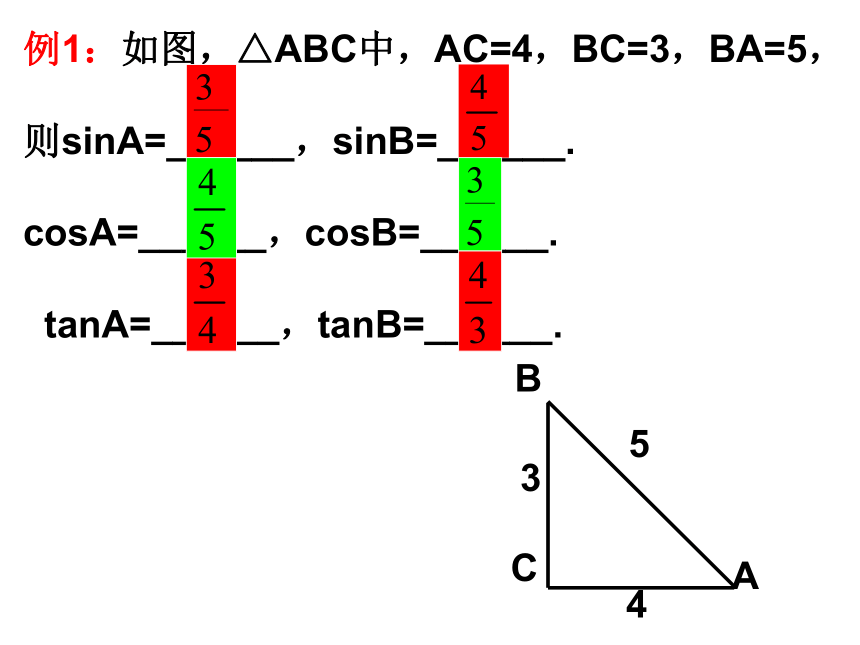
课件16张PPT。三角函数 一、基本定义: 例1:如图,△ABC中,AC=4,BC=3,BA=5,
则sinA=______,sinB=______.
cosA=______,cosB=______.
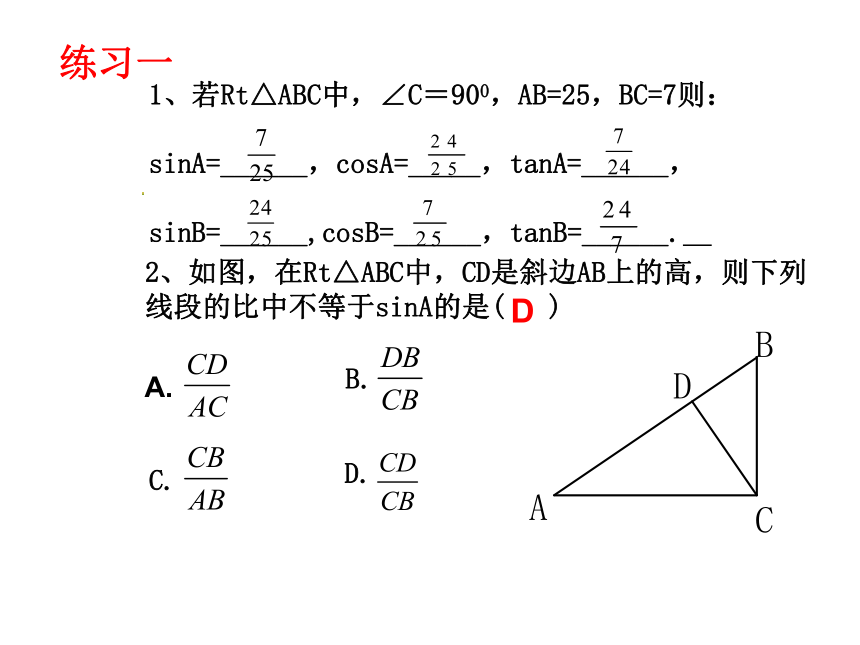
tanA=______,tanB=______.1、若Rt△ABC中,∠C=900,AB=25,BC=7则:
sinA=______,cosA=_____,tanA=______,
sinB=______,cosB=______,tanB=______. 2、如图,在Rt△ABC中,CD是斜边AB上的高,则下列线段的比中不等于sinA的是( ) B. C. D. A.练习一D正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.增大增大减小二、三角函数的增减性:异名函数化为同名函数 例、比较大小:
(1)sin250____sin430
(2)cos70____cos80
(3)sin480____cos520
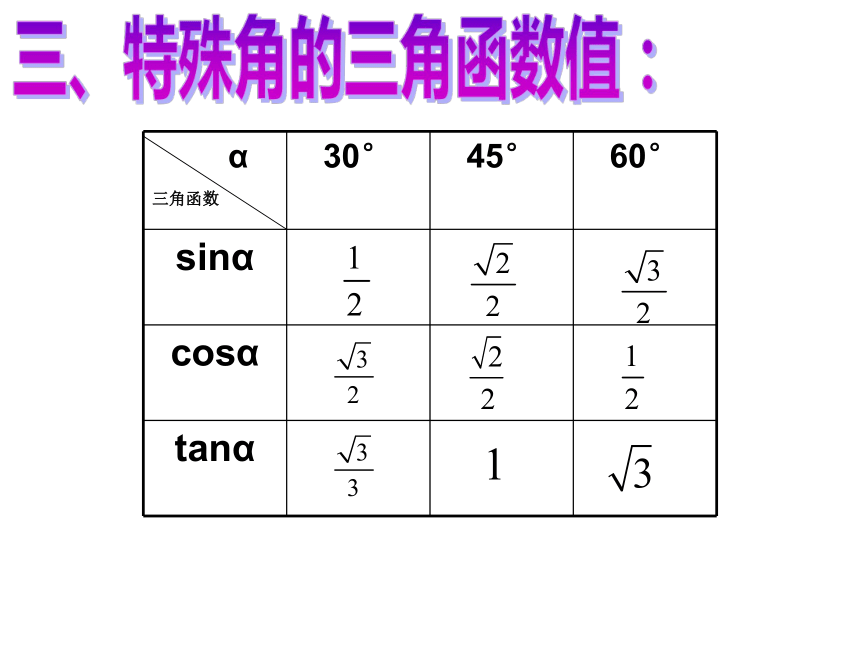
(4)tan480____tan400><>>三、特殊角的三角函数值:例1、计算:例2、已知△ABC满足
则△ABC是______三角形.等边
例3、求适合下列等式的锐角α。
由三角函数值求锐角:1、在直角三角形中,利用已知的元素求出所有未知元素的过程,叫解直角三角形.2、知道直角三角形中的2个元素(至少有一边),可以求出其它三个元素.例3、如图,在△ABC中,∠A=30°,tanB= AC= ,求AB的长.例1、在△ABC中,∠C=90°,a= ,b=2,解这个直角三角形.D 例2、在△ABC中,∠C=900, ,解这个直角三角形。 五、锐角三角函数的应用例、如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为 ,测得乙楼底部D处的俯角为 ,求乙楼的高度.1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想.作业:
复习题2,,4,6,7
则sinA=______,sinB=______.
cosA=______,cosB=______.
tanA=______,tanB=______.1、若Rt△ABC中,∠C=900,AB=25,BC=7则:
sinA=______,cosA=_____,tanA=______,
sinB=______,cosB=______,tanB=______. 2、如图,在Rt△ABC中,CD是斜边AB上的高,则下列线段的比中不等于sinA的是( ) B. C. D. A.练习一D正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.增大增大减小二、三角函数的增减性:异名函数化为同名函数 例、比较大小:
(1)sin250____sin430
(2)cos70____cos80
(3)sin480____cos520
(4)tan480____tan400><>>三、特殊角的三角函数值:例1、计算:例2、已知△ABC满足
则△ABC是______三角形.等边
例3、求适合下列等式的锐角α。
由三角函数值求锐角:1、在直角三角形中,利用已知的元素求出所有未知元素的过程,叫解直角三角形.2、知道直角三角形中的2个元素(至少有一边),可以求出其它三个元素.例3、如图,在△ABC中,∠A=30°,tanB= AC= ,求AB的长.例1、在△ABC中,∠C=90°,a= ,b=2,解这个直角三角形.D 例2、在△ABC中,∠C=900, ,解这个直角三角形。 五、锐角三角函数的应用例、如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为 ,测得乙楼底部D处的俯角为 ,求乙楼的高度.1.数形结合思想.方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形.解题思想与方法小结:2.方程思想.3.转化(化归)思想.作业:
复习题2,,4,6,7
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
