江苏省徐州市睢宁县宁海外国语学校苏科版七年级数学下册(新)《7-1 探索直线平行的条件》课件
文档属性
| 名称 | 江苏省徐州市睢宁县宁海外国语学校苏科版七年级数学下册(新)《7-1 探索直线平行的条件》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-23 00:00:00 | ||
图片预览

文档简介
课件20张PPT。
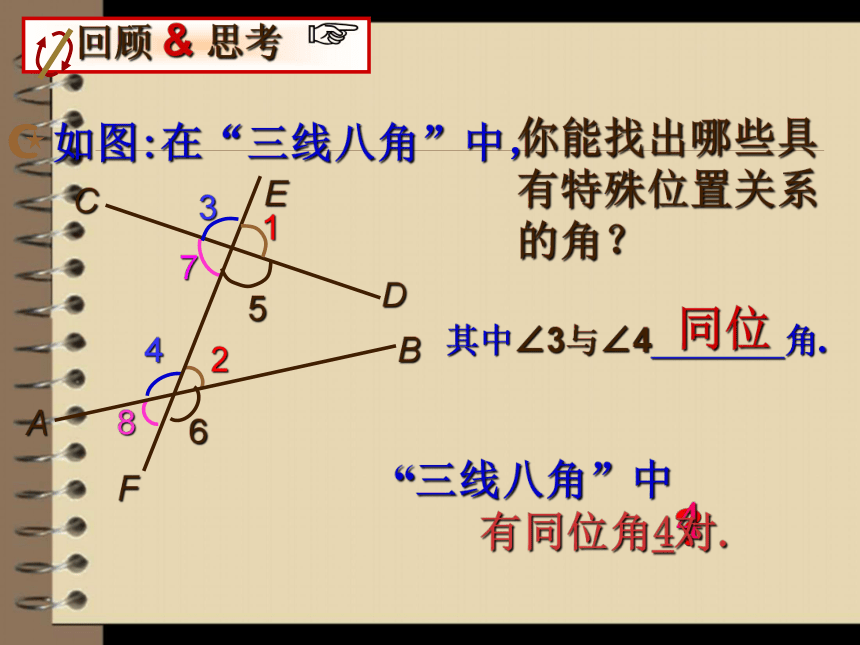
7.1探索直线平行的条件你能找出哪些具有特殊位置关系的角?其中∠3与∠4 角.同位4 “三线八角”中
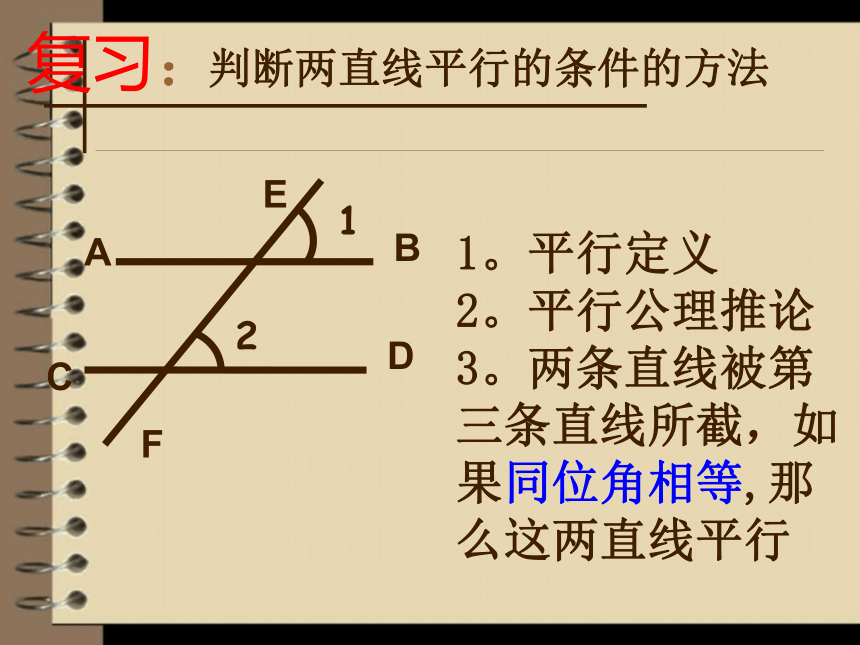
有同位角4对.若∠3=∠4,则直线AB与CD有何位置关系呢?ACF判断两直线平行的条件的方法1。平行定义
2。平行公理推论
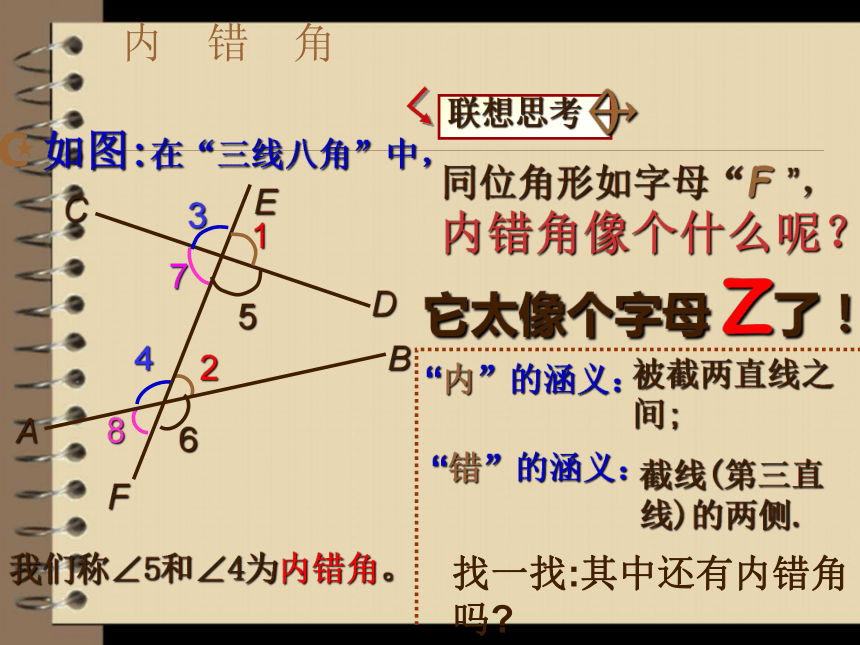
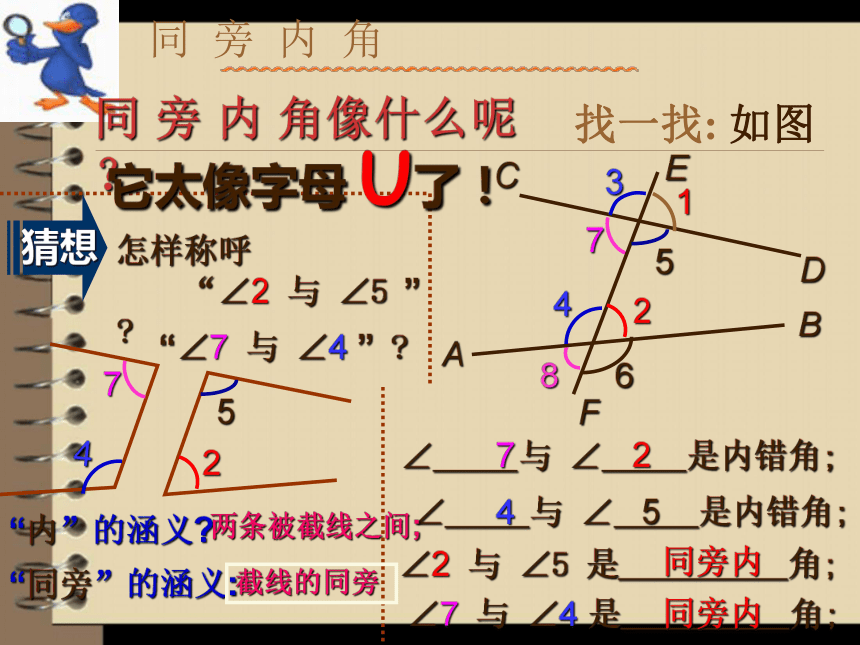
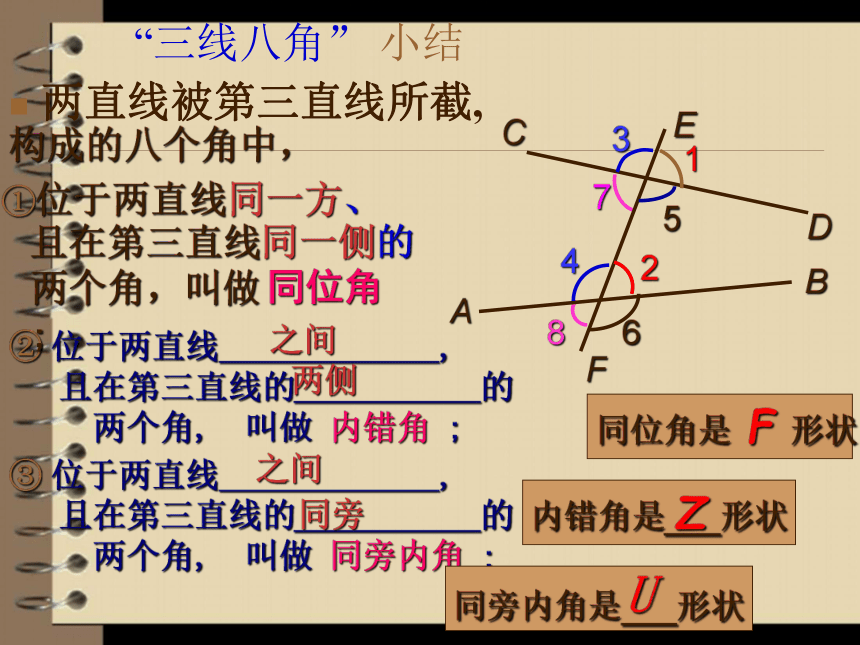
3。两条直线被第三条直线所截,如果同位角相等,那么这两直线平行复习:内错角像个什么呢?我们称∠5和∠4为内错角。它太像个字母 Z了!内 错 角被截两直线之间;“错”的涵义:截线(第三直线)的两侧.找一找:其中还有内错角吗?同 旁 内 角72∠ 与 ∠ 是内错角;4 5同旁内同旁内找一找: 如图“内”的涵义?“同旁”的涵义:两条被截线之间;截线的同旁同 旁 内 角像什么呢?它太像字母 U了!“三线八角” 小结构成的八个角中, 两直线被第三直线所截, ①位于两直线同一方、 ② 位于两直线 ,
且在第三直线的 的
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角之间两侧③ 位于两直线 ,
且在第三直线的 的
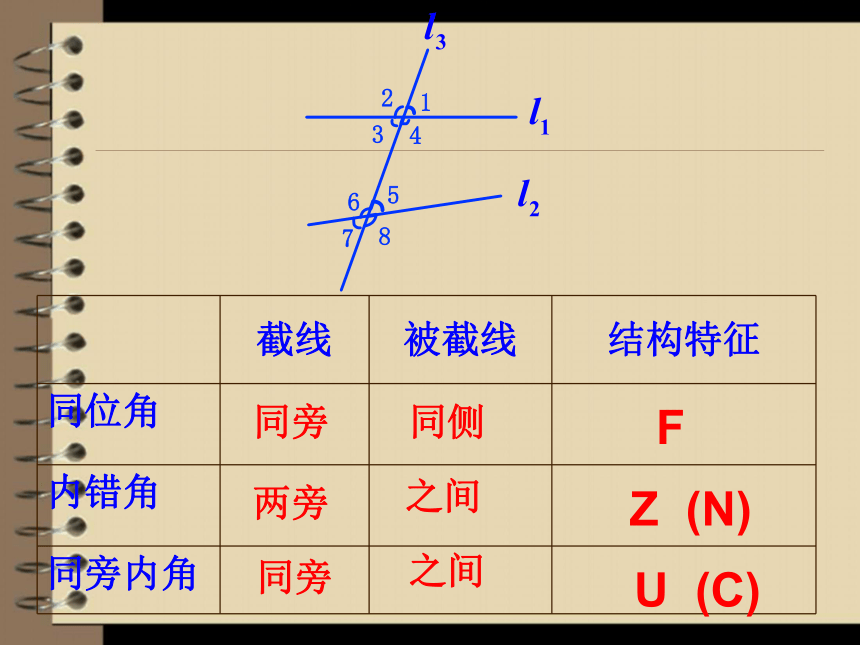
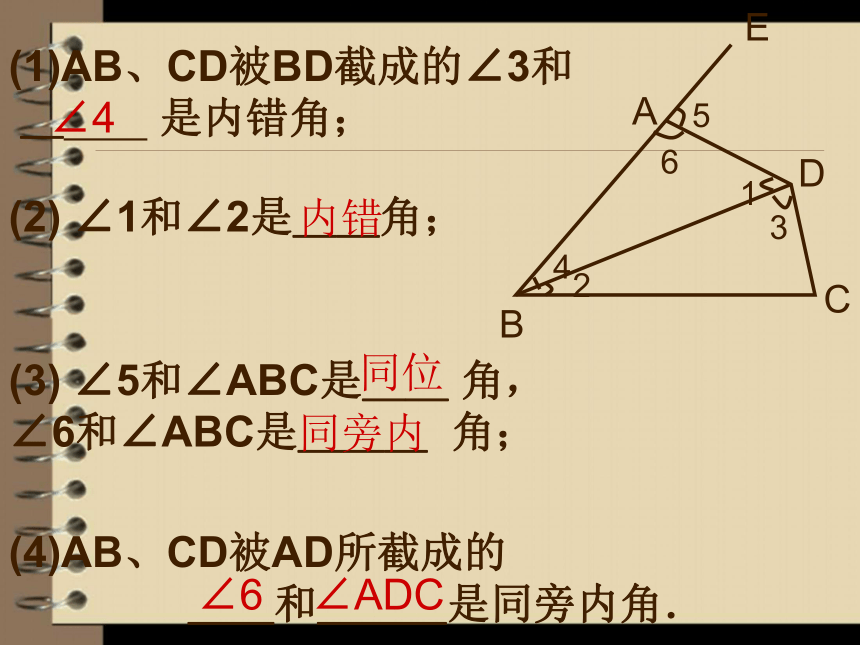
两个角, 叫做 同旁内角 ; 之间同旁ZU之间之间同侧同旁两旁同旁FZ (N)U (C)(1)AB、CD被BD截成的∠3和
_ 是内错角;∠4(2) ∠1和∠2是__角;(3) ∠5和∠ABC是__ 角,
∠6和∠ABC是___ 角;(4)AB、CD被AD所截成的
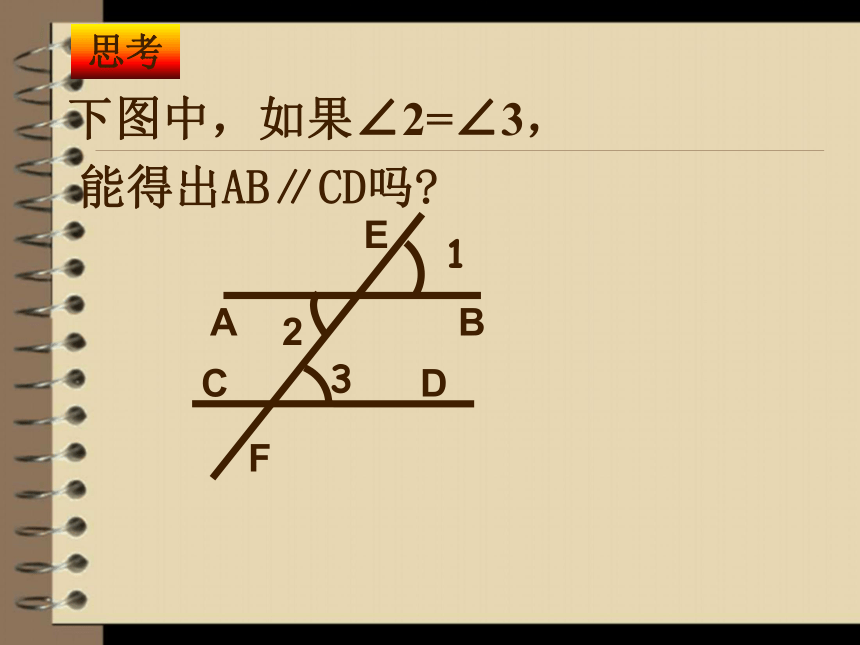
__和___是同旁内角.内错同位同旁内 ∠6∠ADC下图中,如果∠2=∠3,
能得出AB∥CD吗?思考B2ACDF13E证明: ∵ ∠2 = ∠1, ( )对顶角相等 ∠2 = ∠3, ( ) 已知∴ ∠3 = ∠1; ( )∴ 直线 a∥b. ( ). 等量代换同位角相等,两直线平行.同位角相等对顶角相等内错角相等两直线平行的条件: 两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.C下图中,如果∠1+∠2=180°,
能得出AB∥CD?思考证明: ∵ ∠2 + ∠1=180, ( ) ∠1+ ∠3=180, ( ) 已知∴ ∠3 = ∠2; ( ) ∴ 直线 AB∥CD . ( ). 同角的补角相等同位角相等,两直线平行同位角相等两角互补两角互补3邻补角定义两直线平行的条件: 两条直线被第三条直线所截,
如果同旁内角互补,那么这两直线平行.两直线平行 的 判定应用: 如图:∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行?为什么?ADBFCE12思考:
当∠2=______时,DE∥BC
( )
当∠A=______时,AB∥EF
( )∠EFC∠FEC内错角相等,两直线平行同位角相等,两直线平行 1、观察右图并填空:
∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; 随堂练习banm23145∠4∠3∠2a∥b.l∥m.l∥n .① 同位角有4对:② 内错角有2对:③ 同旁内角有2对:∠1和∠2,∠3和∠4,∠5和∠6,∠7和∠8.∠7和∠2,∠5和∠4.∠7和∠4,∠5和∠2如何根据已知条件,说明(证明)两直线平行? 同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.布置作业:补充习题 课本习题
7.1探索直线平行的条件你能找出哪些具有特殊位置关系的角?其中∠3与∠4 角.同位4 “三线八角”中
有同位角4对.若∠3=∠4,则直线AB与CD有何位置关系呢?ACF判断两直线平行的条件的方法1。平行定义
2。平行公理推论
3。两条直线被第三条直线所截,如果同位角相等,那么这两直线平行复习:内错角像个什么呢?我们称∠5和∠4为内错角。它太像个字母 Z了!内 错 角被截两直线之间;“错”的涵义:截线(第三直线)的两侧.找一找:其中还有内错角吗?同 旁 内 角72∠ 与 ∠ 是内错角;4 5同旁内同旁内找一找: 如图“内”的涵义?“同旁”的涵义:两条被截线之间;截线的同旁同 旁 内 角像什么呢?它太像字母 U了!“三线八角” 小结构成的八个角中, 两直线被第三直线所截, ①位于两直线同一方、 ② 位于两直线 ,
且在第三直线的 的
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角之间两侧③ 位于两直线 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ; 之间同旁ZU之间之间同侧同旁两旁同旁FZ (N)U (C)(1)AB、CD被BD截成的∠3和
_ 是内错角;∠4(2) ∠1和∠2是__角;(3) ∠5和∠ABC是__ 角,
∠6和∠ABC是___ 角;(4)AB、CD被AD所截成的
__和___是同旁内角.内错同位同旁内 ∠6∠ADC下图中,如果∠2=∠3,
能得出AB∥CD吗?思考B2ACDF13E证明: ∵ ∠2 = ∠1, ( )对顶角相等 ∠2 = ∠3, ( ) 已知∴ ∠3 = ∠1; ( )∴ 直线 a∥b. ( ). 等量代换同位角相等,两直线平行.同位角相等对顶角相等内错角相等两直线平行的条件: 两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.C下图中,如果∠1+∠2=180°,
能得出AB∥CD?思考证明: ∵ ∠2 + ∠1=180, ( ) ∠1+ ∠3=180, ( ) 已知∴ ∠3 = ∠2; ( ) ∴ 直线 AB∥CD . ( ). 同角的补角相等同位角相等,两直线平行同位角相等两角互补两角互补3邻补角定义两直线平行的条件: 两条直线被第三条直线所截,
如果同旁内角互补,那么这两直线平行.两直线平行 的 判定应用: 如图:∠1=∠2, ∠B+∠BDE=180°.图中哪些线互相平行?为什么?ADBFCE12思考:
当∠2=______时,DE∥BC
( )
当∠A=______时,AB∥EF
( )∠EFC∠FEC内错角相等,两直线平行同位角相等,两直线平行 1、观察右图并填空:
∠1 与 是同位角;
(2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; 随堂练习banm23145∠4∠3∠2a∥b.l∥m.l∥n .① 同位角有4对:② 内错角有2对:③ 同旁内角有2对:∠1和∠2,∠3和∠4,∠5和∠6,∠7和∠8.∠7和∠2,∠5和∠4.∠7和∠4,∠5和∠2如何根据已知条件,说明(证明)两直线平行? 同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.布置作业:补充习题 课本习题
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
