19.1.1.1常量与变量(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 19.1.1.1常量与变量(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-19 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.1.1.1
常量与变量
情景引入
万物皆变,大到天体、小到分子都处在不停的运动变化之中,
如何从数学的角度来刻画这些运动变化并寻找规律呢
背灯和月就花阴,已是十年踪迹十年心。
浮云一别后,流水十年间。
怀旧空吟闻笛赋,到乡翻似烂柯人。
年年岁岁花相似,岁岁年年人不同。
黄晨清水三山下,变更千年如走马。
新知探究
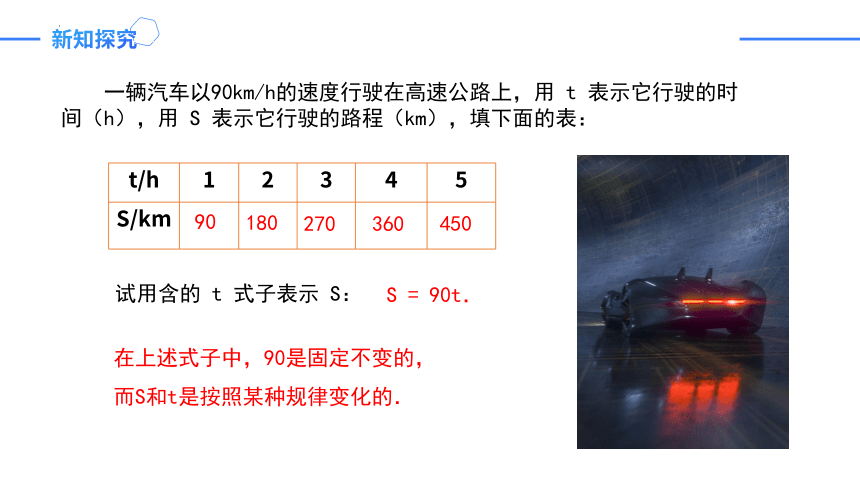
试用含的 t 式子表示 S:
S = 90t.
t/h 1 2 3 4 5
S/km
在上述式子中,90是固定不变的,
而S和t是按照某种规律变化的.
一辆汽车以90km/h的速度行驶在高速公路上,用 t 表示它行驶的时间(h),用 S 表示它行驶的路程(km),填下面的表:
90
180
270
360
450
新知探究
当电流表的读数为1安时,滑动变阻器接入电路的电阻R为12欧姆;
一个滑动变阻器串联在电路中,已知电源电压V=12伏,
电流表测量串联电路的电流I.
在上述式子中,12是固定不变的,而电阻R和电流I是按照某种规律变化的.
当电流表的读数为2安时,滑动变阻器接入电路的电阻R为6欧姆;
当电流表的读数为3安时,滑动变阻器接入电路的电阻R为4欧姆;
当电流表的读数为6安时,滑动变阻器接入电路的电阻R为2欧姆;
新知探究
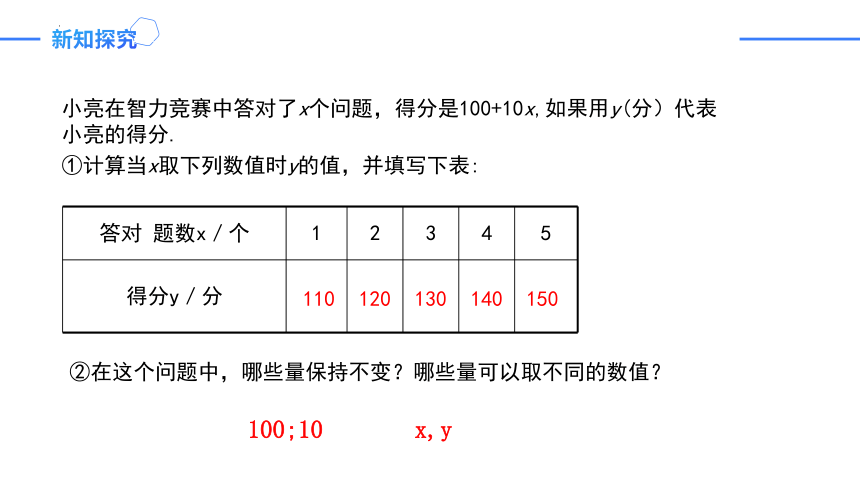
小亮在智力竞赛中答对了x个问题,得分是100+10x,如果用y(分)代表小亮的得分.
①计算当x取下列数值时y的值,并填写下表:
答对 题数x/个 1 2 3 4 5
得分y/分
110
120
130
140
150
②在这个问题中,哪些量保持不变?哪些量可以取不同的数值?
100;10
x,y
新知探究
小明设计了一个计算机程序,输入和输出的数据如下表:
输入(x) … 1 2 3 4 …
输出(y) … 1 4 9 16 …
当输入的数据是8和10时,输出的数据分别是多少?
当输入的数据用x来表示时,输出的数据y怎样用关于x的代数式表示?
y=x2
64
100
新知探究
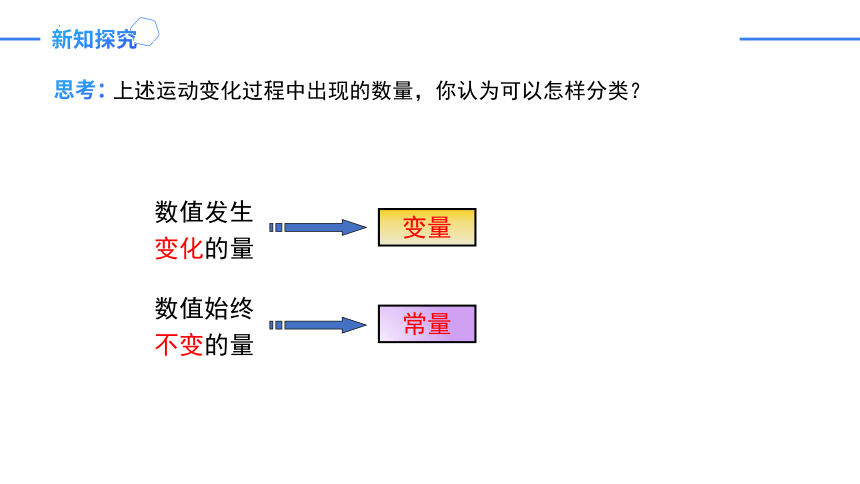
思考:
数值发生
变化的量
变量
数值始终
不变的量
常量
上述运动变化过程中出现的数量,你认为可以怎样分类?
新知探究
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
请指出上面各个变化过程中的常量、变量.
在同一个变化过程中,理解变量与常量的关键词:发生了变化和始终不变.
y=x2
S=90t
R=12/I
y=100+10x
新知探究
思考:
哪些量保持不变?哪些量可以取不同的数值?分别把它们指出来.
变量
常量
y=x2
S=90t
R=12/I
y=100+10x
y , x
S , t
R , I
y , x
1
90
12
100,10
新知探究
填空:
1.汽车以80千米/小时的速度行驶,用t时表示行驶的时间,s千米表示行驶路程,其中常量是 ,变量是 .
2.汽车行驶200千米的路程,用v千米/小时表示行驶的速度,t时表示行驶的时间,其中常量是 ,变量是 .
3.在行程问题中,s=vt,s 一定时,常量是 ,变量是 .
80千米/时
t时, s千米
200千米
v千米/小时,t时
s
V,t
新知探究
4.长方形的长和宽分别是a与b,周长C=2(a+b),其中常量是 ,变量是 .
5.圆锥体积v与圆锥底面半径r圆锥高h之间存在关系式v=(1/3)πr2h,其中常量是 ,变量是 .
2
C,a,b
1/3,π
v,r,h
6.购买一些钢笔,单价2元/支,总价y元随钢笔支数x变化,指出其中的常量与变量,并写出关系式.
y=2x
常量为:2;变量为x,y.
新知探究
7.某水果店橘子的单价为2.5元/千克,记买k千克橘子的总价为s元。请写出关系式并说出其中的常量和变量.
S=2.5k
变量是S,k
常量是2.5
8.某种杂志每册定价5.80元,买3册应付款17.4元;买5册应付款29元;
如果买x册,应付款y元,那么y用关于x的代数式表示y=5.8x.
保持不变的量是定价,可以取不同的数值的量是册数和付款金额。
新知探究
9.将10m长的绳子围成长方形,计算长方形的长为3m时,
该长方形的面积为多少?
解:当长方形的长为3时,
面积=3×(10-2×3)÷2 = 6,
设长方形的边长为 l m,面积为S m2,怎样用含l的式子表示S?
S=l(10-2l)÷2
S=5l-l2
当长方形的长为4时,
面积=4×(10-2×4)÷2 = 4,
在上述式子中,10、-2是固定不变的,
而S和l是按照某种规律变化的.
常量与变量
典例精析
1
2
变量与常量是相对的,在不同的变化过程中,二者可以相互转化,判断变量与常量的前提是“在某一个变化过程中”.例如:在s=vt中,当s一定时,v,t是变量,s是常量;当t一定时,s,v是变量,t是常量.
变量、常量与字母指数没有关系,如在S=中,不能说r2是变量.
3
注意不是变量,而是常量.
典例精析
例1
指出下列关系式中的变量与常量:
(1) y = 3x -4,
(2) y=x,
(3) y= x2+2x-8,
(4) S = πr2.
解:(1)3和-4是常量,x和y是变量.
(2)1是常量,x、y是变量.
(3)1、2、-8是常量,x、y是变量.
(4)兀是常量,s、r是变量.
典例精析
例2
写出下列各问题中的函数关系式,并指出其中的常量与变量:
(1)圆的周长c与半径r的关系式;
(2)N(n>2)边形的内角和的度数s与边数n的函数关系式;
(3)等腰三角形的顶角度数y与底角度数x的关系式;
c= 2πr,常量是2π,变量是和 r.
s=180°(n-2),常量是 180°,2,变量是n和 S.
y=180°-2x,常量是 180°,2,变量是x和 y.
S=x(30-x),常量是 60,变量是和 S.
V=πR2h/3,常量是 R/3,变量是和 V.
(4)一个周长为 60的长方形,一边长为 ,其面积为;
(5)假设圆柱的底面半径不变,圆柱的高为,圆柱的体积为 V.
典例精析
例3
底边 上的高是 ,当 的顶点 沿底边 向点 运动时,三角形的面积发生了变化,如图所示.
如果 的底边 长为 ,那么 的面积 可以表示为 .
()在这个过程中,常量是 ,变量是 ;
()当底边长从 12 变化到3 时,三角形的面积从 2变化到 2.
( ) =3x中,常量是 3,变量是 x 与 y.
( )当 x=12时, y=36;当 x=3 时, y=9.
即三角形的面积从 36 2 ,变化到 9 2 .
典例精析
例4
瓶子或罐头盒等物体常如下图所示堆放,试确定瓶子总数y与层数x之间的关系式.
1 2 3 … n
y …
1
1+2
1+2+3
1+2+3+ …+n
完成上表,并写出瓶子总数y 与层数x之间的关系式
x
归纳总结
常量与变量
常量与变量的概念
列出变量之间的关系式
常量:数值始终不变的量
变量:数值发生变化的量
当堂检测
1.某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A、数100和η,t都是变量
B、数100和η都是常量
C、η和t是变量
D、数100和t都是常量
C
2.中国电信公司最近推出的无线市话的收费标准为:前3 min(不足3 min按3 min计)收费0.2元,3 min后每分钟0.1元.则通话一次的时间x(min)(x>3)与这次通话费用y(元)之间的关系是( )
A.y=0.1x B.y=0.2+0.1x
C.y=0.2+0.1(x-3) D.y=0.1x+0.5
C
当堂检测
3.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n
C.y=2n+1+n D.y=2n+n+1
B
当堂检测
4.某学校乒乓球协会计划购买100元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为____________.
n= 100/a
y=30n
5.某教科书的单价是30元,则总金额y(元)与学生数n(个)的关系式是_________.
6.正方体的棱长为a与其表面积S之间的关系是________,与其体积V之间的关系是__________.
S=6a2
V=a3
a
当堂检测
7.收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标
刻的.下面是一些对应的数值:
观察上表回答:
(1)波长l 和频率f 数值之间有什么关系
(2)波长l 越大,频率f 就________.
(3)在这个问题中,哪些量是变量?哪些量是常量?
解 :(1) l 与 f 的乘积是一个定值,即
lf=300 000,
或者说
(2)波长l 越大,频率f 就越小 .
(3)变量是:波长、频率,常量是:300 000.
当堂检测
8.购买一些铅笔,单价为0.2元/支,总价y元随铅笔支数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
解:y=0.2x (x是大于或等于0的整数),其中0.2为常量,
x,y为变量,x为自变量,y是x的函数.
9.一个三角形的底边长为5,高h可以任意伸缩. 写出面积 S随h变化的解析式,并指出其中的常量与变量,自变量与函数,以及自变量的取值范围.
解: ,h>0, 为常量,S,h为变量,h为自变
量,S是h的函数.
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.1.1.1
常量与变量
情景引入
万物皆变,大到天体、小到分子都处在不停的运动变化之中,
如何从数学的角度来刻画这些运动变化并寻找规律呢
背灯和月就花阴,已是十年踪迹十年心。
浮云一别后,流水十年间。
怀旧空吟闻笛赋,到乡翻似烂柯人。
年年岁岁花相似,岁岁年年人不同。
黄晨清水三山下,变更千年如走马。
新知探究
试用含的 t 式子表示 S:
S = 90t.
t/h 1 2 3 4 5
S/km
在上述式子中,90是固定不变的,
而S和t是按照某种规律变化的.
一辆汽车以90km/h的速度行驶在高速公路上,用 t 表示它行驶的时间(h),用 S 表示它行驶的路程(km),填下面的表:
90
180
270
360
450
新知探究
当电流表的读数为1安时,滑动变阻器接入电路的电阻R为12欧姆;
一个滑动变阻器串联在电路中,已知电源电压V=12伏,
电流表测量串联电路的电流I.
在上述式子中,12是固定不变的,而电阻R和电流I是按照某种规律变化的.
当电流表的读数为2安时,滑动变阻器接入电路的电阻R为6欧姆;
当电流表的读数为3安时,滑动变阻器接入电路的电阻R为4欧姆;
当电流表的读数为6安时,滑动变阻器接入电路的电阻R为2欧姆;
新知探究
小亮在智力竞赛中答对了x个问题,得分是100+10x,如果用y(分)代表小亮的得分.
①计算当x取下列数值时y的值,并填写下表:
答对 题数x/个 1 2 3 4 5
得分y/分
110
120
130
140
150
②在这个问题中,哪些量保持不变?哪些量可以取不同的数值?
100;10
x,y
新知探究
小明设计了一个计算机程序,输入和输出的数据如下表:
输入(x) … 1 2 3 4 …
输出(y) … 1 4 9 16 …
当输入的数据是8和10时,输出的数据分别是多少?
当输入的数据用x来表示时,输出的数据y怎样用关于x的代数式表示?
y=x2
64
100
新知探究
思考:
数值发生
变化的量
变量
数值始终
不变的量
常量
上述运动变化过程中出现的数量,你认为可以怎样分类?
新知探究
变量:在一个变化过程中,数值发生变化的量为变量.
常量:在一个变化过程中,数值始终不变的量为常量.
请指出上面各个变化过程中的常量、变量.
在同一个变化过程中,理解变量与常量的关键词:发生了变化和始终不变.
y=x2
S=90t
R=12/I
y=100+10x
新知探究
思考:
哪些量保持不变?哪些量可以取不同的数值?分别把它们指出来.
变量
常量
y=x2
S=90t
R=12/I
y=100+10x
y , x
S , t
R , I
y , x
1
90
12
100,10
新知探究
填空:
1.汽车以80千米/小时的速度行驶,用t时表示行驶的时间,s千米表示行驶路程,其中常量是 ,变量是 .
2.汽车行驶200千米的路程,用v千米/小时表示行驶的速度,t时表示行驶的时间,其中常量是 ,变量是 .
3.在行程问题中,s=vt,s 一定时,常量是 ,变量是 .
80千米/时
t时, s千米
200千米
v千米/小时,t时
s
V,t
新知探究
4.长方形的长和宽分别是a与b,周长C=2(a+b),其中常量是 ,变量是 .
5.圆锥体积v与圆锥底面半径r圆锥高h之间存在关系式v=(1/3)πr2h,其中常量是 ,变量是 .
2
C,a,b
1/3,π
v,r,h
6.购买一些钢笔,单价2元/支,总价y元随钢笔支数x变化,指出其中的常量与变量,并写出关系式.
y=2x
常量为:2;变量为x,y.
新知探究
7.某水果店橘子的单价为2.5元/千克,记买k千克橘子的总价为s元。请写出关系式并说出其中的常量和变量.
S=2.5k
变量是S,k
常量是2.5
8.某种杂志每册定价5.80元,买3册应付款17.4元;买5册应付款29元;
如果买x册,应付款y元,那么y用关于x的代数式表示y=5.8x.
保持不变的量是定价,可以取不同的数值的量是册数和付款金额。
新知探究
9.将10m长的绳子围成长方形,计算长方形的长为3m时,
该长方形的面积为多少?
解:当长方形的长为3时,
面积=3×(10-2×3)÷2 = 6,
设长方形的边长为 l m,面积为S m2,怎样用含l的式子表示S?
S=l(10-2l)÷2
S=5l-l2
当长方形的长为4时,
面积=4×(10-2×4)÷2 = 4,
在上述式子中,10、-2是固定不变的,
而S和l是按照某种规律变化的.
常量与变量
典例精析
1
2
变量与常量是相对的,在不同的变化过程中,二者可以相互转化,判断变量与常量的前提是“在某一个变化过程中”.例如:在s=vt中,当s一定时,v,t是变量,s是常量;当t一定时,s,v是变量,t是常量.
变量、常量与字母指数没有关系,如在S=中,不能说r2是变量.
3
注意不是变量,而是常量.
典例精析
例1
指出下列关系式中的变量与常量:
(1) y = 3x -4,
(2) y=x,
(3) y= x2+2x-8,
(4) S = πr2.
解:(1)3和-4是常量,x和y是变量.
(2)1是常量,x、y是变量.
(3)1、2、-8是常量,x、y是变量.
(4)兀是常量,s、r是变量.
典例精析
例2
写出下列各问题中的函数关系式,并指出其中的常量与变量:
(1)圆的周长c与半径r的关系式;
(2)N(n>2)边形的内角和的度数s与边数n的函数关系式;
(3)等腰三角形的顶角度数y与底角度数x的关系式;
c= 2πr,常量是2π,变量是和 r.
s=180°(n-2),常量是 180°,2,变量是n和 S.
y=180°-2x,常量是 180°,2,变量是x和 y.
S=x(30-x),常量是 60,变量是和 S.
V=πR2h/3,常量是 R/3,变量是和 V.
(4)一个周长为 60的长方形,一边长为 ,其面积为;
(5)假设圆柱的底面半径不变,圆柱的高为,圆柱的体积为 V.
典例精析
例3
底边 上的高是 ,当 的顶点 沿底边 向点 运动时,三角形的面积发生了变化,如图所示.
如果 的底边 长为 ,那么 的面积 可以表示为 .
()在这个过程中,常量是 ,变量是 ;
()当底边长从 12 变化到3 时,三角形的面积从 2变化到 2.
( ) =3x中,常量是 3,变量是 x 与 y.
( )当 x=12时, y=36;当 x=3 时, y=9.
即三角形的面积从 36 2 ,变化到 9 2 .
典例精析
例4
瓶子或罐头盒等物体常如下图所示堆放,试确定瓶子总数y与层数x之间的关系式.
1 2 3 … n
y …
1
1+2
1+2+3
1+2+3+ …+n
完成上表,并写出瓶子总数y 与层数x之间的关系式
x
归纳总结
常量与变量
常量与变量的概念
列出变量之间的关系式
常量:数值始终不变的量
变量:数值发生变化的量
当堂检测
1.某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A、数100和η,t都是变量
B、数100和η都是常量
C、η和t是变量
D、数100和t都是常量
C
2.中国电信公司最近推出的无线市话的收费标准为:前3 min(不足3 min按3 min计)收费0.2元,3 min后每分钟0.1元.则通话一次的时间x(min)(x>3)与这次通话费用y(元)之间的关系是( )
A.y=0.1x B.y=0.2+0.1x
C.y=0.2+0.1(x-3) D.y=0.1x+0.5
C
当堂检测
3.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n
C.y=2n+1+n D.y=2n+n+1
B
当堂检测
4.某学校乒乓球协会计划购买100元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为____________.
n= 100/a
y=30n
5.某教科书的单价是30元,则总金额y(元)与学生数n(个)的关系式是_________.
6.正方体的棱长为a与其表面积S之间的关系是________,与其体积V之间的关系是__________.
S=6a2
V=a3
a
当堂检测
7.收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标
刻的.下面是一些对应的数值:
观察上表回答:
(1)波长l 和频率f 数值之间有什么关系
(2)波长l 越大,频率f 就________.
(3)在这个问题中,哪些量是变量?哪些量是常量?
解 :(1) l 与 f 的乘积是一个定值,即
lf=300 000,
或者说
(2)波长l 越大,频率f 就越小 .
(3)变量是:波长、频率,常量是:300 000.
当堂检测
8.购买一些铅笔,单价为0.2元/支,总价y元随铅笔支数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
解:y=0.2x (x是大于或等于0的整数),其中0.2为常量,
x,y为变量,x为自变量,y是x的函数.
9.一个三角形的底边长为5,高h可以任意伸缩. 写出面积 S随h变化的解析式,并指出其中的常量与变量,自变量与函数,以及自变量的取值范围.
解: ,h>0, 为常量,S,h为变量,h为自变
量,S是h的函数.
