人教版六年级下册数学圆柱、圆锥训练课运用解题策略-探究规律课件(共31张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆柱、圆锥训练课运用解题策略-探究规律课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 256.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 08:40:54 | ||
图片预览





文档简介
(共31张PPT)
——圆柱、圆锥训练课
运用解题策略 探究规律
问题:
一个圆柱和一个圆锥,底面周长比
是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
A .9:4 B . 3:2 C. 9:2
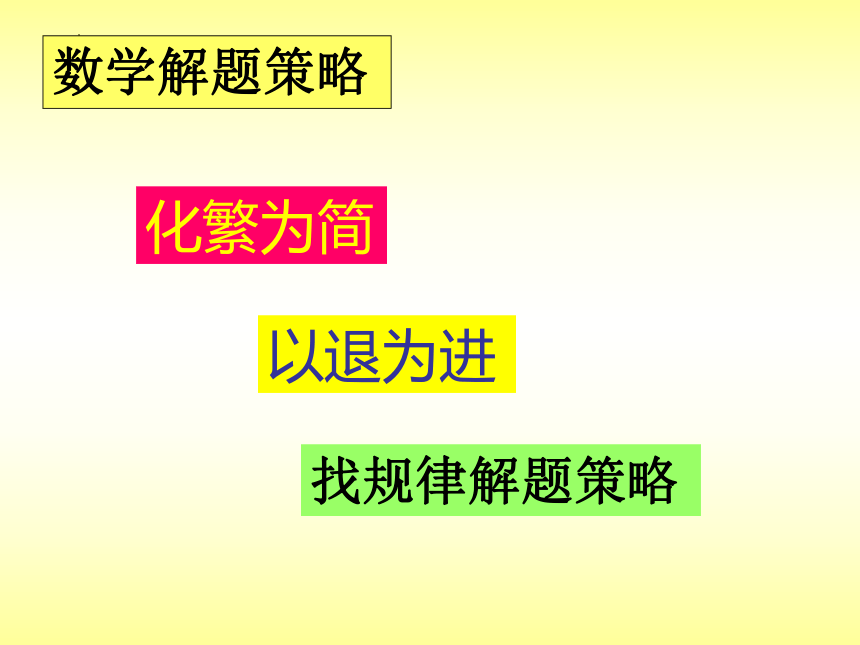
化繁为简
以退为进
找规律解题策略
数学解题策略
一个圆柱和一个圆锥,底面周长比
是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
怎么退?
退到哪?
以退为进
圆的半径变化引起圆的周长、面积变化的规律
o
o
①
②
o
o
①
②
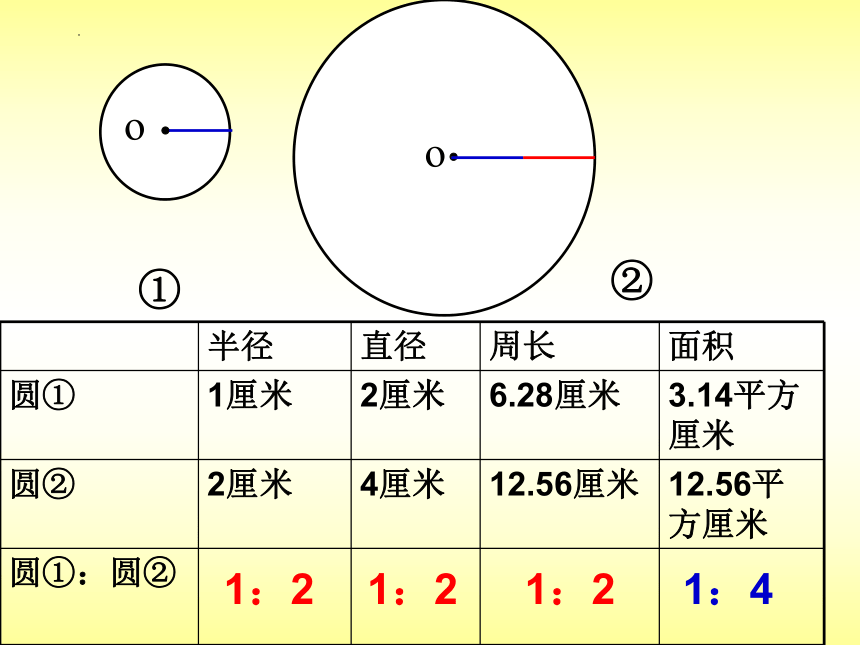
半径 直径 周长 面积
圆① 1厘米 2厘米 6.28厘米 3.14平方厘米
圆② 2厘米 4厘米 12.56厘米 12.56平方厘米
圆①:圆②
1:2
1:2
1:2
1:4
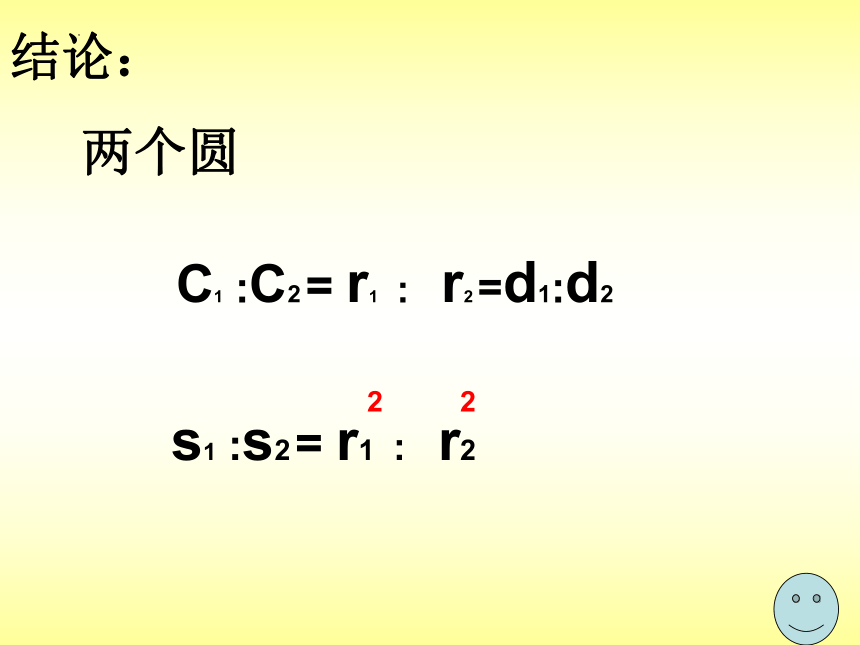
结论:
两个圆
s1 :s2 = r1 : r2
2
2
C1 :C2 = r1 : r2 =d1:d2
一个圆柱(或圆锥),底面半径
变化、高变化引起侧面积和体积
变化的规律
o
o
①
高不变
底面半径扩大2倍。高不变,
侧面积怎样变化?
体积怎样变化?
o
①
底面半径不变。高缩小到原来的 ,
侧面积怎样变化?
体积怎样变化?
o
o
①
底面半径扩大2倍。高缩小到原来的 ,
侧面积怎样变化?
体积怎样变化?
o
结论:
圆柱的高不变,底面半径扩大几倍,侧面积也扩大几倍,体积扩大半径的平方倍。
圆柱的底面半径不变,高扩大几倍,侧面积扩大几倍,体积也扩大几倍。
圆柱的底面半径变化,高也变化,侧面积变化是半径和高的变化的倍数的乘积,体积变化是半径变化的平方倍与高的变化的乘积。
两个圆柱(或圆锥)等高,底面积变化引起侧面积和体积变化的规律。
o
o
①
②
高相等
底面半径比1:2
o
o
①
②
圆柱①:
圆柱②
底面半径比
底面直径比
底面周长比
底面积比
侧面积比
体积比
1:2
1:2
1:2
等高
底面半径比1:2
1:4
1:2
1:4
1:2
1:2
1:2
1:2
1:4
1:4
o
o
A
B
o
结论:两个圆柱(或圆锥),等高前提下:
v1:v2 = s1底 :s2 底= r1 : r2
2
2
s1侧:s2侧= c1 底:c2底= r1 : r2
两个圆柱(或圆锥)等底,不等高,高的变化引起体积变化的规律
底面积不变,两个圆柱高的比是3:4,
体积比( )。
底面积不变,两个圆锥高的比还是3:4,
圆锥体积比是( )。
o
o
①
②
3:4
3:4
结论:底面积相等的前提下,两个
圆柱(或圆锥),高的比就是体积比。
两个圆柱(或圆锥)不等底、不等高,圆柱的侧面积比?体积比?圆锥的体积比?的变化规律。
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
s1侧:s2侧=
V柱1:v柱2=
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
s1侧:s2侧
=c1h1 :c2h2
=(1×2):(2×3)
=2:6
=1:3
r1:r2=1:2
c1 : c2=1:2
h1 : h2=2:3
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
V1:V2
=S1h1 :S2h2
=(1×2):(4×3)
=2:12
=1:6
r1:r2=1:2
s1 : s2=1:4
h1 : h2=2:3
结论:两个圆柱(或圆锥),侧面积的比等于底面半径与高的乘积的比。体积比等于底面半径的平方与高的乘积的比。
s1侧 : s2侧
= c1h1 : c2h2
= (r1 ×h1) : (r2 ×h2)
V1 : V2
=S1 h1 : S2 h2
= (r1 ×h1) : (r2 × h2)
2
2
一个圆柱和一个圆锥,不等底,不等高,体积比的变化规律。
一个圆柱和一个圆锥底面半径比是
2:3,圆柱和圆锥高的比是3:4,
圆柱和圆锥的体积比是( ):( )。
一个圆柱和一个圆锥底面半径比是
2:3,圆柱和圆锥高的比是3:4,
圆柱和圆锥的体积比是( ):( )。
(2×2×3):( × 3×3×4)
1 1
练习:
一个圆柱和一个圆锥,底面周长比是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
A .9:4 B .3:2 C.9:2
C
(1)两个圆柱底面半径比是
3:2,高相等,两个圆柱的体积比是( ): ( ) ,两个圆柱的侧面积比是( ): ( )
9
4
3
2
(2)一个圆锥的底面直径是一个圆柱的底面直径的 ,
它们的高相等,那么圆锥体积是圆柱体积的( )
A .
B .
C.
B
——圆柱、圆锥训练课
运用解题策略 探究规律
问题:
一个圆柱和一个圆锥,底面周长比
是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
A .9:4 B . 3:2 C. 9:2
化繁为简
以退为进
找规律解题策略
数学解题策略
一个圆柱和一个圆锥,底面周长比
是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
怎么退?
退到哪?
以退为进
圆的半径变化引起圆的周长、面积变化的规律
o
o
①
②
o
o
①
②
半径 直径 周长 面积
圆① 1厘米 2厘米 6.28厘米 3.14平方厘米
圆② 2厘米 4厘米 12.56厘米 12.56平方厘米
圆①:圆②
1:2
1:2
1:2
1:4
结论:
两个圆
s1 :s2 = r1 : r2
2
2
C1 :C2 = r1 : r2 =d1:d2
一个圆柱(或圆锥),底面半径
变化、高变化引起侧面积和体积
变化的规律
o
o
①
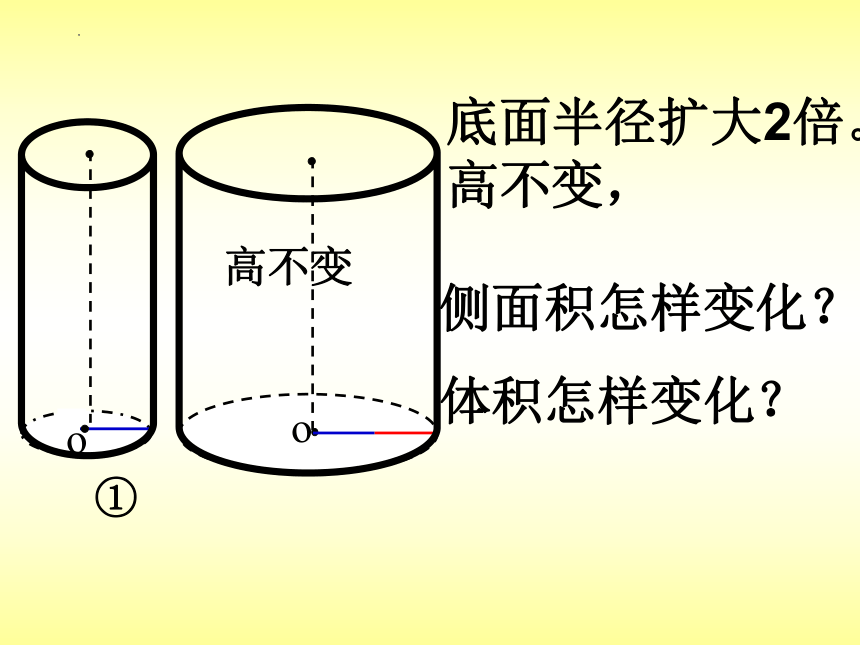
高不变
底面半径扩大2倍。高不变,
侧面积怎样变化?
体积怎样变化?
o
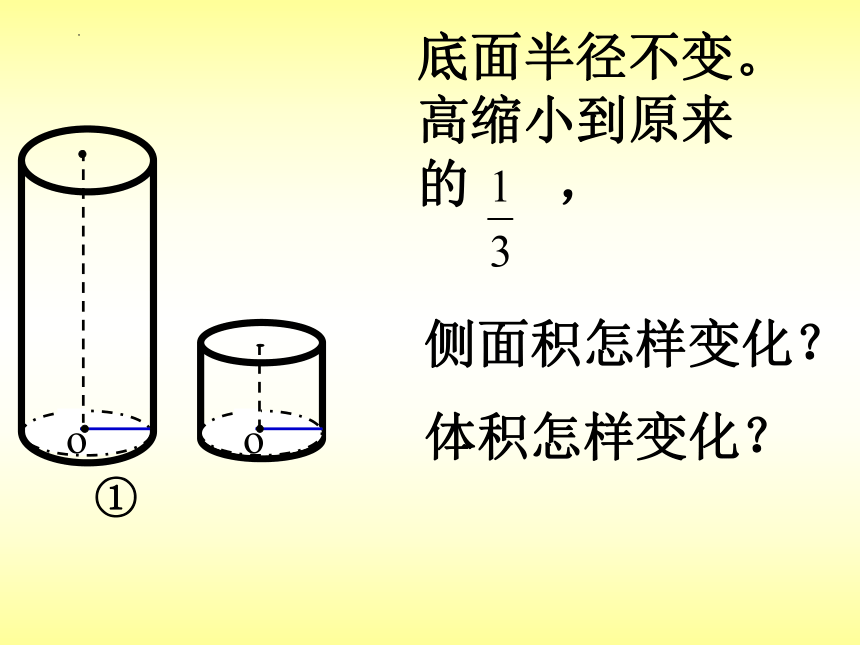
①
底面半径不变。高缩小到原来的 ,
侧面积怎样变化?
体积怎样变化?
o
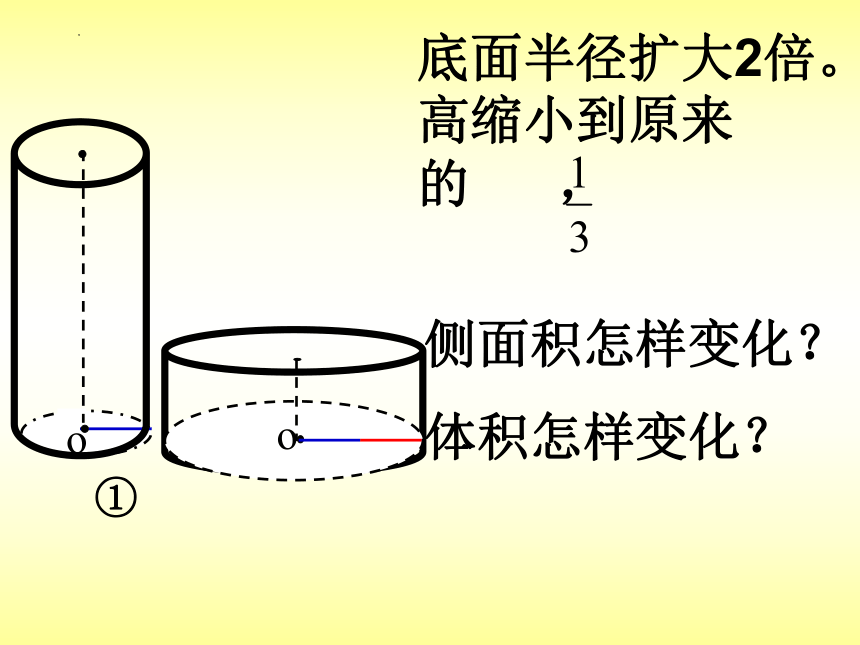
o
①
底面半径扩大2倍。高缩小到原来的 ,
侧面积怎样变化?
体积怎样变化?
o
结论:
圆柱的高不变,底面半径扩大几倍,侧面积也扩大几倍,体积扩大半径的平方倍。
圆柱的底面半径不变,高扩大几倍,侧面积扩大几倍,体积也扩大几倍。
圆柱的底面半径变化,高也变化,侧面积变化是半径和高的变化的倍数的乘积,体积变化是半径变化的平方倍与高的变化的乘积。
两个圆柱(或圆锥)等高,底面积变化引起侧面积和体积变化的规律。
o
o
①
②
高相等
底面半径比1:2
o
o
①
②
圆柱①:
圆柱②
底面半径比
底面直径比
底面周长比
底面积比
侧面积比
体积比
1:2
1:2
1:2
等高
底面半径比1:2
1:4
1:2
1:4
1:2
1:2
1:2
1:2
1:4
1:4
o
o
A
B
o
结论:两个圆柱(或圆锥),等高前提下:
v1:v2 = s1底 :s2 底= r1 : r2
2
2
s1侧:s2侧= c1 底:c2底= r1 : r2
两个圆柱(或圆锥)等底,不等高,高的变化引起体积变化的规律
底面积不变,两个圆柱高的比是3:4,
体积比( )。
底面积不变,两个圆锥高的比还是3:4,
圆锥体积比是( )。
o
o
①
②
3:4
3:4
结论:底面积相等的前提下,两个
圆柱(或圆锥),高的比就是体积比。
两个圆柱(或圆锥)不等底、不等高,圆柱的侧面积比?体积比?圆锥的体积比?的变化规律。
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
s1侧:s2侧=
V柱1:v柱2=
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
s1侧:s2侧
=c1h1 :c2h2
=(1×2):(2×3)
=2:6
=1:3
r1:r2=1:2
c1 : c2=1:2
h1 : h2=2:3
o
o
①
②
已知:
h1:h2=2:3
r1:r2=1:2
V1:V2
=S1h1 :S2h2
=(1×2):(4×3)
=2:12
=1:6
r1:r2=1:2
s1 : s2=1:4
h1 : h2=2:3
结论:两个圆柱(或圆锥),侧面积的比等于底面半径与高的乘积的比。体积比等于底面半径的平方与高的乘积的比。
s1侧 : s2侧
= c1h1 : c2h2
= (r1 ×h1) : (r2 ×h2)
V1 : V2
=S1 h1 : S2 h2
= (r1 ×h1) : (r2 × h2)
2
2
一个圆柱和一个圆锥,不等底,不等高,体积比的变化规律。
一个圆柱和一个圆锥底面半径比是
2:3,圆柱和圆锥高的比是3:4,
圆柱和圆锥的体积比是( ):( )。
一个圆柱和一个圆锥底面半径比是
2:3,圆柱和圆锥高的比是3:4,
圆柱和圆锥的体积比是( ):( )。
(2×2×3):( × 3×3×4)
1 1
练习:
一个圆柱和一个圆锥,底面周长比是3:2,高的比是2:3,这个圆柱和圆锥的体积比是( ):( )。
A .9:4 B .3:2 C.9:2
C
(1)两个圆柱底面半径比是
3:2,高相等,两个圆柱的体积比是( ): ( ) ,两个圆柱的侧面积比是( ): ( )
9
4
3
2
(2)一个圆锥的底面直径是一个圆柱的底面直径的 ,
它们的高相等,那么圆锥体积是圆柱体积的( )
A .
B .
C.
B
