北师大版优化方案必修一第一章章末优化总结
文档属性
| 名称 | 北师大版优化方案必修一第一章章末优化总结 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-23 00:00:00 | ||
图片预览

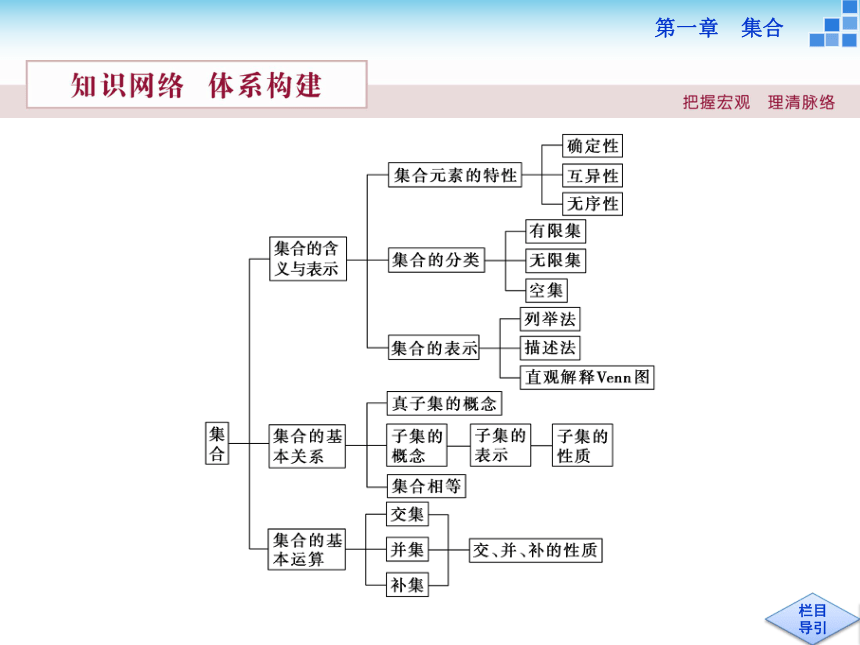







文档简介
课件21张PPT。章末优化总结第一章 集合集合的概念与表示集合的概念与表示是集合运算的基础,主要有两类问题:一是集合元素的三大特性,二是用适当的方法表示集合. (1)已知集合A={x∈N|x<6},则下列关系式错误的是
( )
A.0∈A B.1.5?A
C.-1?A D.6∈A
(2)集合A={(x,y)|x+y=10,x∈N+,y∈N+}的元素个数为
( )
A.8 B.9
C.10 D.100DB[解析] (1)A={x∈N|x<6}={0,1,2,3,4,5},6?A.
(2)A={(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1)},
所以A中共9个元素.集合的基本关系 D集合的基本运算集合的基本运算有交集、并集和补集,进行集合的运算时,首先关注集合的表示方法,对于用描述法表示的集合,认清元素一般符号的意义;一般地,有限数集的运算可以用观察法或Venn图法,无限数集的运算可以借助数轴,点集的运算可以借助图像,当然对集合的交、并、补运算也可直接用定义求解. 已知集合A={x|4≤x<8},B={x|2(1)求A∪B;(?RA)∩B;
(2)若A∩C≠?,求a的取值范围.
[解] (1)A∪B={x|2?RA={x|x<4或x≥8},
(?RA)∩B={x|2(2)若A∩C≠?,由数轴知a>4.创新型集合问题创新型集合问题主要有新定义、新性质和新运算等问题,关键是准确理解新定义、新性质和新运算,转化为运用集合的有关知识求解.1.集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为( )
A.0 B.1
C.2 D.4
解析:由A、B集合元素的互异性知a≠0,a≠1,a≠2,故选D.DD2.设P,Q是两个非空集合,定义P×Q={(a,b)|a∈P,b∈Q},若P={3,4,5},Q={4,5,6,7},则P×Q中元素的个数是( )
A.3 B.4
C.7 D.12
解析:a有3种取值,b有4种取值,P×Q中元素(a,b)有(3,4),(3,5),(3,6),(3,7);(4,4),(4,5),(4,6),(4,7);(5,4),(5,5),(5,6),(5,7).共12个.3.设集合A={-1,0,3},B={a+3,2a+1},A∩B={3},则实数a的值为________.
解析:由题意知3∈B,所以a+3=3或2a+1=3,所以a=0或a=1.
4.集合A={1,2,3,5},当x∈A时,若x-1?A,且x+1?A,则称x为A的一个“孤立元素”,则A中孤立元素的个数为________.
解析:因为x=5时,x-1=4?A,x+1=6?A,
所以A中的孤立元素为5.0或115.已知集合M={x|x2-3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(?RN);
(2)若M∪N=M,求实数a的取值范围.本部分内容讲解结束按ESC键退出全屏播放
( )
A.0∈A B.1.5?A
C.-1?A D.6∈A
(2)集合A={(x,y)|x+y=10,x∈N+,y∈N+}的元素个数为
( )
A.8 B.9
C.10 D.100DB[解析] (1)A={x∈N|x<6}={0,1,2,3,4,5},6?A.
(2)A={(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1)},
所以A中共9个元素.集合的基本关系 D集合的基本运算集合的基本运算有交集、并集和补集,进行集合的运算时,首先关注集合的表示方法,对于用描述法表示的集合,认清元素一般符号的意义;一般地,有限数集的运算可以用观察法或Venn图法,无限数集的运算可以借助数轴,点集的运算可以借助图像,当然对集合的交、并、补运算也可直接用定义求解. 已知集合A={x|4≤x<8},B={x|2
(2)若A∩C≠?,求a的取值范围.
[解] (1)A∪B={x|2
(?RA)∩B={x|2
A.0 B.1
C.2 D.4
解析:由A、B集合元素的互异性知a≠0,a≠1,a≠2,故选D.DD2.设P,Q是两个非空集合,定义P×Q={(a,b)|a∈P,b∈Q},若P={3,4,5},Q={4,5,6,7},则P×Q中元素的个数是( )
A.3 B.4
C.7 D.12
解析:a有3种取值,b有4种取值,P×Q中元素(a,b)有(3,4),(3,5),(3,6),(3,7);(4,4),(4,5),(4,6),(4,7);(5,4),(5,5),(5,6),(5,7).共12个.3.设集合A={-1,0,3},B={a+3,2a+1},A∩B={3},则实数a的值为________.
解析:由题意知3∈B,所以a+3=3或2a+1=3,所以a=0或a=1.
4.集合A={1,2,3,5},当x∈A时,若x-1?A,且x+1?A,则称x为A的一个“孤立元素”,则A中孤立元素的个数为________.
解析:因为x=5时,x-1=4?A,x+1=6?A,
所以A中的孤立元素为5.0或115.已知集合M={x|x2-3x≤10},N={x|a+1≤x≤2a+1}.
(1)若a=2,求M∩(?RN);
(2)若M∪N=M,求实数a的取值范围.本部分内容讲解结束按ESC键退出全屏播放
