二元一次方程组(广东省广州市天河区)
文档属性
| 名称 | 二元一次方程组(广东省广州市天河区) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-19 00:00:00 | ||
图片预览






文档简介
课件18张PPT。 8.1二元一次方程组问题: 篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少?等量关系:胜的场数+负的场数=总场数胜场积分+负场积分=总积分昨天,我们8个人去公园玩,买门票花了34元。
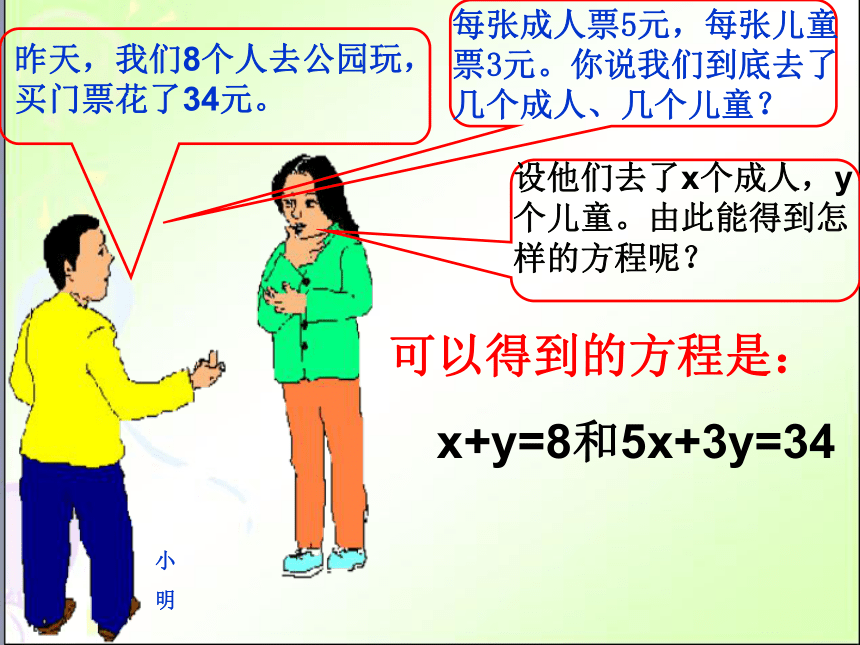
每张成人票5元,每张儿童票3元。你说我们到底去了几个成人、几个儿童?可以得到的方程是:
x+y=8和5x+3y=34小 明 含有两个未知数,并且未知数的项的次数都是 1,像这样的方程叫做二元一次方程。学习新知讨论:一个二元一次方程的解唯一吗? 适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解。二元一次方程的解:如x=6,y=2方程x+y=8的一个解,记作
同样 也是方程x+y=8的一个解。x=6y=2 把具有相同未知数的两个二元一次方程合在一起,就组成一个二元一次方程组。例如
都是二元一次方程组。 做一做试一试:
1、找出方程1的解
2、找出方程2的解
3、哪些即是方程1的解又是方程2的解?二元一次方程组的解 二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解。例如 就是二元一次方程
组 的解. x=5y=3x+y=85x+3y=34B,DA,BB巩固新知例1.(1)若3xm+1+5y2-n =3是一个二元一次方程,
则m=_______,n=________. 01练习:
课本95页习题8.1复习巩固1、2题
课本94页练习
目前我们找出二元一次方程组的解只能从两个方程中找出公共解,具体的解法下节课才讲。探究:对于x+2y=5,思考下列问题:(3)取一个你自己喜欢的数作为x的值,求所对应的y 的值;(2)用含x的式子表示y;(1)用含y的式子表示x;在此基础上,我们了解了二元一次方程、二元一次
方程组的概念,并学会了判断一组数是不是某个
方程的解的方法.通过这节课的学习,我们 进一步体会到了方程
是刻画现实世界的有效的数学模型.课堂感悟1.已知 是二元一次方程ax+3y=7
的解,则 a= 。 1随堂练习3.如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( ) ABCDC作业:
完成练习卷
每张成人票5元,每张儿童票3元。你说我们到底去了几个成人、几个儿童?可以得到的方程是:
x+y=8和5x+3y=34小 明 含有两个未知数,并且未知数的项的次数都是 1,像这样的方程叫做二元一次方程。学习新知讨论:一个二元一次方程的解唯一吗? 适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解。二元一次方程的解:如x=6,y=2方程x+y=8的一个解,记作
同样 也是方程x+y=8的一个解。x=6y=2 把具有相同未知数的两个二元一次方程合在一起,就组成一个二元一次方程组。例如
都是二元一次方程组。 做一做试一试:
1、找出方程1的解
2、找出方程2的解
3、哪些即是方程1的解又是方程2的解?二元一次方程组的解 二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解。例如 就是二元一次方程
组 的解. x=5y=3x+y=85x+3y=34B,DA,BB巩固新知例1.(1)若3xm+1+5y2-n =3是一个二元一次方程,
则m=_______,n=________. 01练习:
课本95页习题8.1复习巩固1、2题
课本94页练习
目前我们找出二元一次方程组的解只能从两个方程中找出公共解,具体的解法下节课才讲。探究:对于x+2y=5,思考下列问题:(3)取一个你自己喜欢的数作为x的值,求所对应的y 的值;(2)用含x的式子表示y;(1)用含y的式子表示x;在此基础上,我们了解了二元一次方程、二元一次
方程组的概念,并学会了判断一组数是不是某个
方程的解的方法.通过这节课的学习,我们 进一步体会到了方程
是刻画现实世界的有效的数学模型.课堂感悟1.已知 是二元一次方程ax+3y=7
的解,则 a= 。 1随堂练习3.如图所示,将长方形ABCD的一个角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x ,y度,那么x,y所适合的一个方程组是( ) ABCDC作业:
完成练习卷
