2024年苏科版数学中考一模复习专题讲义 专题11-锐角三角函数
文档属性
| 名称 | 2024年苏科版数学中考一模复习专题讲义 专题11-锐角三角函数 |

|
|
| 格式 | docx | ||
| 文件大小 | 596.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览


文档简介
2023-2024学年苏科版数学中考一模复习专题讲义
(专题11-锐角三角函数)
【考点一】锐角三角形函数的概念
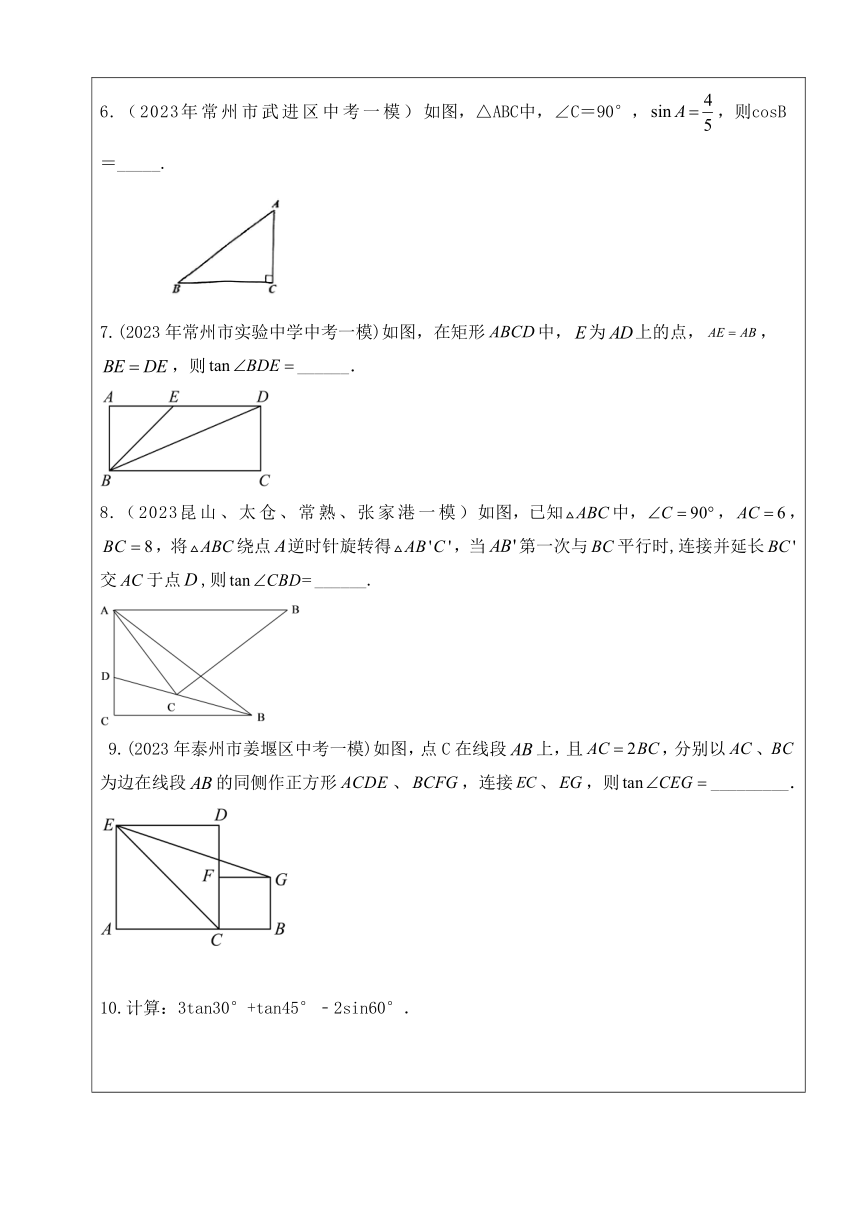
【知识梳理】 在Rt△ABC中,∠C=90° 1、正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA,即sinA== 2、余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA,即cosA= 3、正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA,即tanA= 4、三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。 【一模典型例题】 1.tan45°的值等于( ) A.2 B.1 C. D. 2.在△ABC中,∠C=90°,AB=5,BC=4,那么∠A的正弦值是( ) A. B. C. D. 3.2sin45°的值为( ) A. B.1 C. D. 4.在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sinA的值为 . 5.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sinA的值为 . 6.(2023年常州市武进区中考一模)如图,△ABC中,∠C=90°,,则cosB=_____. 7.(2023年常州市实验中学中考一模)如图,在矩形中,为上的点,,,则______. 8.(2023昆山、太仓、常熟、张家港一模)如图,已知中,,,,将绕点逆时针旋转得,当第一次与平行时,连接并延长交于点,则______. 9.(2023年泰州市姜堰区中考一模)如图,点C在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则_________. 10.计算:3tan30°+tan45°﹣2sin60°.
【考点二】锐角三角函数在网格三角形中的运用
【知识梳理】 解直角三角形常用关系 (1)锐角、直角之间的关系:∠A+∠B=90°; (2)三边之间的关系:a2+b2=c2; (3)边角之间的关系: sinA=,cosA=,tanA=(a,b,c分别是∠A、∠B、∠C的对边) 2、 sin30°=; cos30°=;tan30°=;
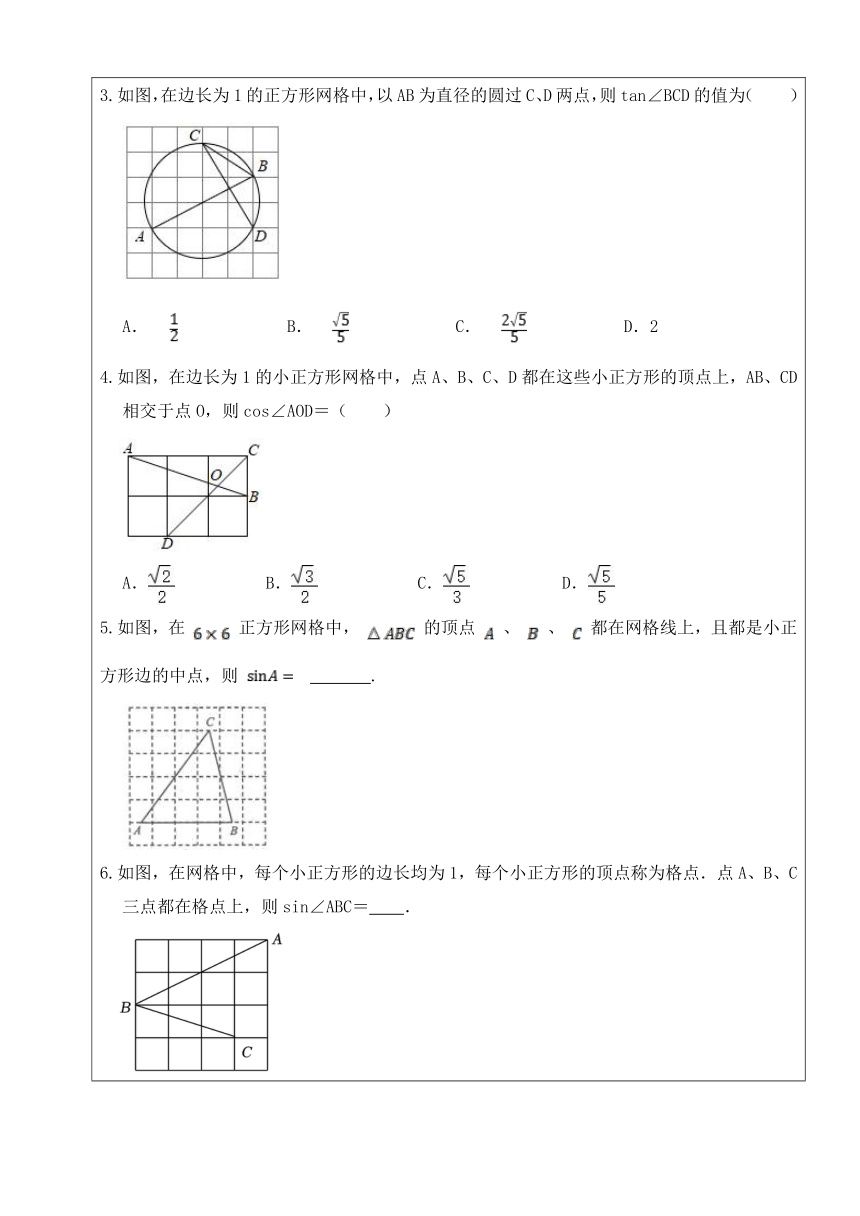
sin45°=;cos45°=;tan45°=1; sin60°=;cos60°=; tan60°=; 【一模典型例题】 1.(2023年淮安市涟水县中考数学一模试卷)如图,,,是正方形网格的格点,连接,,则的值是( ) A. B. C. D. 2.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( ) A. B. C.2 D. 3.如图,在边长为1的正方形网格中,以AB为直径的圆过C、D两点,则tan∠BCD的值为( ) B. C. D.2 4.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=( ) A. B. C. D. 5.如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 . 6.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则sin∠ABC= . 7.(2023年常州市金坛区中考一模)如图,在边长相同的小正方形组成的网格中,点A、B、O都在这些小正方形的顶点上,那么sin∠AOB的值为______. 8.(2023年连云港海宁中学中考一模数学)如图,在网格正方形中,每个小正方形的边长为1,顶点为格点若的顶点均是格点,则的值是________.
【考点三】锐角三角函数的综合运用
【知识梳理】 1、坡度坡角问题 (1)坡度是坡面的垂直高度h和水平宽度l的比,常用i表示。 (2)坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系:i=h/l=tanα. (3)解决坡度问题,一般通过作高构成直角三角形,坡角是锐角,坡度是锐角的正切值,水平宽度或垂直高度是直角边,本质是解直角三角形问题。 2、仰角俯角问题 (1)概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角。 (2)解决此类问题需要了解角之间的关系,找到与条件和所求相关联的直角三角形,当图形中没有直角三角形时,要通过作高构造直角三角形,把实际问题转化为直角三角形中边角关系问题加以解决。 3、方向角问题 (1)辨别方向角:以第一个方向为始边向另一个方向旋转相应度数。 (2)解决方向角问题,要根据题意理清图形中各角的关系,如果所给方向角不在直角三角形中,可以用“两直线平行,内错角相等”“余角”等知识转化为所需要的角。 【一模典型例题】 1.(2023年南通市如东县、通州区中考一模)如图,学校有一旗杆.为了测量旗杆高度,小明采用如下方案:在点C处测得旗杆顶B的仰角为,从与点C相距的E处测得旗杆顶B的仰角为.若,则旗杆AB的高度为_______米.(结果保留小数点后一位,,). 2.(2023年泰州市靖江市中考一模)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点,、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,计算出建筑物的高度约为 __(参考数据:米. 3.(2023年淮安市洪泽区中考一模)如图,高楼顶部有一信号发射塔(),在矩形建筑物的两点测得该塔顶端F的仰角分别为,矩形建筑物高度为22米.求该信号发射塔顶端到地面的距离.(精确到1m)(参考数据: ) 4.(2023年淮安市淮阴区中考一模)如图,小明在热气球上看到正前方横跨河流两岸大桥,并测得,两点的俯角分别为和,已知大桥的长度为,且与地面在同一水平面上.求热气球离地面的高度(结果保留整数,参考数据:,,,). 5. (2023年泰州市姜堰区中考一模)如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84) 6.(2023年南通市海安市海陵中学中考一模)如图1是一个手机支架,图2是其侧面示意图,,可分别绕点,转动,经测量,,.当,转动到,时,求点到的距离.(结果保留小数点后一位) 参考数据:,,,,,,. 7.(2023年淮安市涟水县中考数学一模试卷)某校数学兴趣小组为了测量建筑物的高度,先在斜坡的底部测得建筑物顶点的仰角为31°,再沿斜坡走了到达斜坡顶点处,,然后在点测得建筑物顶点的仰角为53°,已知斜坡的坡度.(参考数据:,) (1)求点到地面的高度; (2)求建筑物的高度. 8.(2023年连云港海宁中学中考一模数学)小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2.已知,,,,.(结果精确到0.1,参考数据:,,,,,) (1)连结,求线段的长. (2)求点A,B之间的距离.
(专题11-锐角三角函数)
【考点一】锐角三角形函数的概念
【知识梳理】 在Rt△ABC中,∠C=90° 1、正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA,即sinA== 2、余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA,即cosA= 3、正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA,即tanA= 4、三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。 【一模典型例题】 1.tan45°的值等于( ) A.2 B.1 C. D. 2.在△ABC中,∠C=90°,AB=5,BC=4,那么∠A的正弦值是( ) A. B. C. D. 3.2sin45°的值为( ) A. B.1 C. D. 4.在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sinA的值为 . 5.在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sinA的值为 . 6.(2023年常州市武进区中考一模)如图,△ABC中,∠C=90°,,则cosB=_____. 7.(2023年常州市实验中学中考一模)如图,在矩形中,为上的点,,,则______. 8.(2023昆山、太仓、常熟、张家港一模)如图,已知中,,,,将绕点逆时针旋转得,当第一次与平行时,连接并延长交于点,则______. 9.(2023年泰州市姜堰区中考一模)如图,点C在线段上,且,分别以、为边在线段的同侧作正方形、,连接、,则_________. 10.计算:3tan30°+tan45°﹣2sin60°.
【考点二】锐角三角函数在网格三角形中的运用
【知识梳理】 解直角三角形常用关系 (1)锐角、直角之间的关系:∠A+∠B=90°; (2)三边之间的关系:a2+b2=c2; (3)边角之间的关系: sinA=,cosA=,tanA=(a,b,c分别是∠A、∠B、∠C的对边) 2、 sin30°=; cos30°=;tan30°=;
sin45°=;cos45°=;tan45°=1; sin60°=;cos60°=; tan60°=; 【一模典型例题】 1.(2023年淮安市涟水县中考数学一模试卷)如图,,,是正方形网格的格点,连接,,则的值是( ) A. B. C. D. 2.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( ) A. B. C.2 D. 3.如图,在边长为1的正方形网格中,以AB为直径的圆过C、D两点,则tan∠BCD的值为( ) B. C. D.2 4.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=( ) A. B. C. D. 5.如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 . 6.如图,在网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B、C三点都在格点上,则sin∠ABC= . 7.(2023年常州市金坛区中考一模)如图,在边长相同的小正方形组成的网格中,点A、B、O都在这些小正方形的顶点上,那么sin∠AOB的值为______. 8.(2023年连云港海宁中学中考一模数学)如图,在网格正方形中,每个小正方形的边长为1,顶点为格点若的顶点均是格点,则的值是________.
【考点三】锐角三角函数的综合运用
【知识梳理】 1、坡度坡角问题 (1)坡度是坡面的垂直高度h和水平宽度l的比,常用i表示。 (2)坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系:i=h/l=tanα. (3)解决坡度问题,一般通过作高构成直角三角形,坡角是锐角,坡度是锐角的正切值,水平宽度或垂直高度是直角边,本质是解直角三角形问题。 2、仰角俯角问题 (1)概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角。 (2)解决此类问题需要了解角之间的关系,找到与条件和所求相关联的直角三角形,当图形中没有直角三角形时,要通过作高构造直角三角形,把实际问题转化为直角三角形中边角关系问题加以解决。 3、方向角问题 (1)辨别方向角:以第一个方向为始边向另一个方向旋转相应度数。 (2)解决方向角问题,要根据题意理清图形中各角的关系,如果所给方向角不在直角三角形中,可以用“两直线平行,内错角相等”“余角”等知识转化为所需要的角。 【一模典型例题】 1.(2023年南通市如东县、通州区中考一模)如图,学校有一旗杆.为了测量旗杆高度,小明采用如下方案:在点C处测得旗杆顶B的仰角为,从与点C相距的E处测得旗杆顶B的仰角为.若,则旗杆AB的高度为_______米.(结果保留小数点后一位,,). 2.(2023年泰州市靖江市中考一模)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点,、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,计算出建筑物的高度约为 __(参考数据:米. 3.(2023年淮安市洪泽区中考一模)如图,高楼顶部有一信号发射塔(),在矩形建筑物的两点测得该塔顶端F的仰角分别为,矩形建筑物高度为22米.求该信号发射塔顶端到地面的距离.(精确到1m)(参考数据: ) 4.(2023年淮安市淮阴区中考一模)如图,小明在热气球上看到正前方横跨河流两岸大桥,并测得,两点的俯角分别为和,已知大桥的长度为,且与地面在同一水平面上.求热气球离地面的高度(结果保留整数,参考数据:,,,). 5. (2023年泰州市姜堰区中考一模)如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84) 6.(2023年南通市海安市海陵中学中考一模)如图1是一个手机支架,图2是其侧面示意图,,可分别绕点,转动,经测量,,.当,转动到,时,求点到的距离.(结果保留小数点后一位) 参考数据:,,,,,,. 7.(2023年淮安市涟水县中考数学一模试卷)某校数学兴趣小组为了测量建筑物的高度,先在斜坡的底部测得建筑物顶点的仰角为31°,再沿斜坡走了到达斜坡顶点处,,然后在点测得建筑物顶点的仰角为53°,已知斜坡的坡度.(参考数据:,) (1)求点到地面的高度; (2)求建筑物的高度. 8.(2023年连云港海宁中学中考一模数学)小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2.已知,,,,.(结果精确到0.1,参考数据:,,,,,) (1)连结,求线段的长. (2)求点A,B之间的距离.
同课章节目录
