2023-2024学年湖南省益阳市部分学校期末联考试题卷九年级上册数学(含解析)
文档属性
| 名称 | 2023-2024学年湖南省益阳市部分学校期末联考试题卷九年级上册数学(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 00:00:00 | ||
图片预览


文档简介
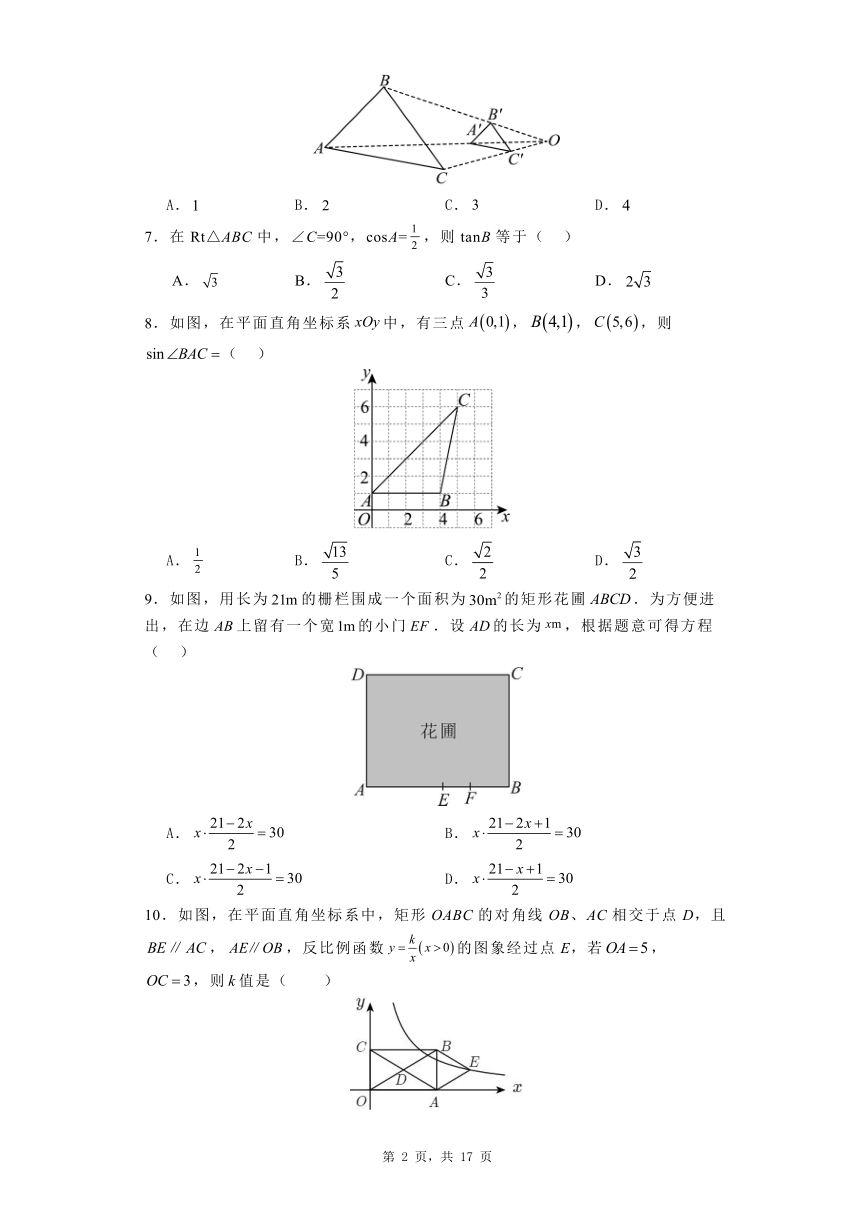
九年级数学(问卷)
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.下列关系式中,是x的反比例函数的是( )
A. B. C. D.
2.如图,在直角坐标系中,一次函数与反比例函数的图象交于A,B两点,下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
3.已知,是一元二次方程的两个根,则的值为( )
A. B. C. D.
4.根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
5.若,则的值为( )
A. B. C. D.
6.如图,与是位似图形,是位似中心,位似比为,若,则的长为( )
A. B. C. D.
7.在Rt△ABC中,∠C=90°,cosA=,则tanB等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,有三点,,,则( )
A. B. C. D.
9.如图,用长为的栅栏围成一个面积为的矩形花圃.为方便进出,在边上留有一个宽的小门.设的长为,根据题意可得方程( )
A. B.
C. D.
10.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且,,反比例函数的图象经过点E,若,,则值是( )
A. B.15 C. D.12
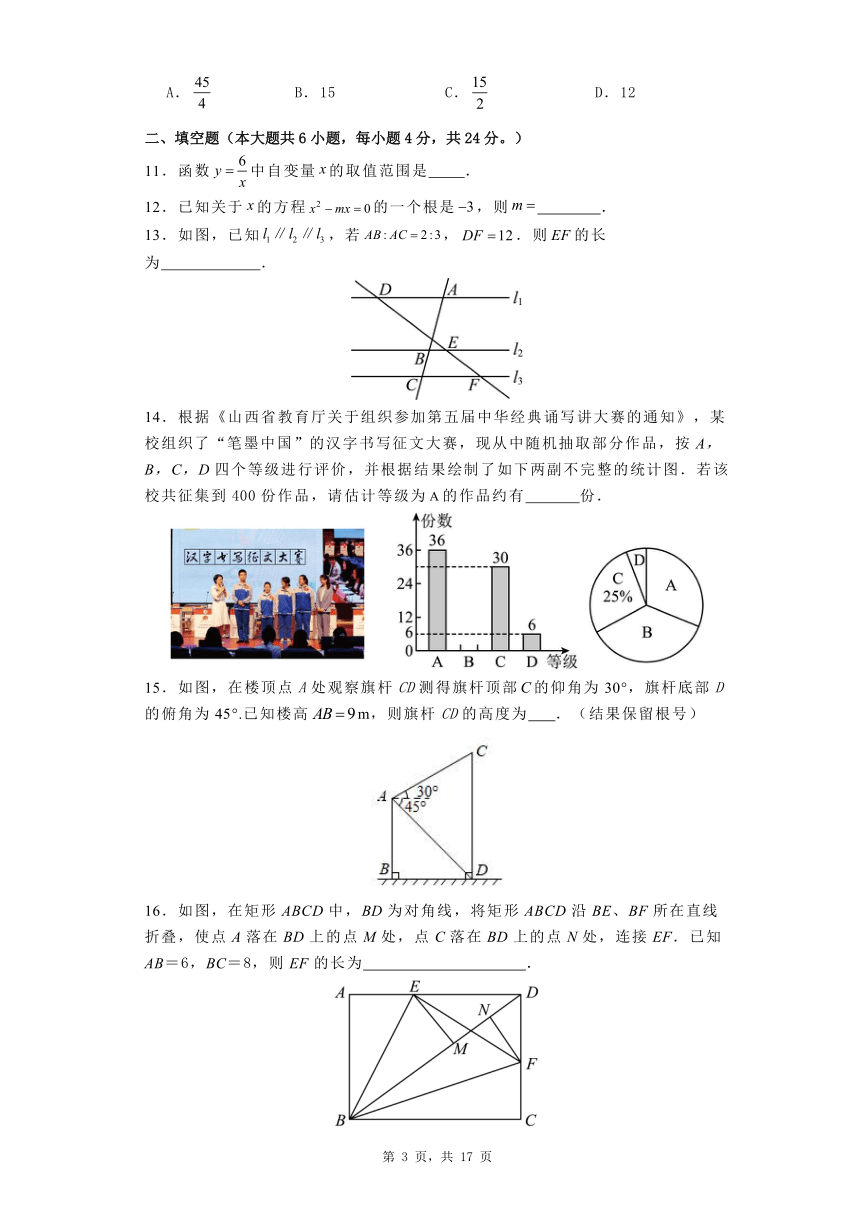
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数中自变量的取值范围是 .
12.已知关于的方程的一个根是,则 .
13.如图,已知,若,.则的长为 .
14.根据《山西省教育厅关于组织参加第五届中华经典诵写讲大赛的通知》,某校组织了“笔墨中国”的汉字书写征文大赛,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两副不完整的统计图.若该校共征集到400份作品,请估计等级为的作品约有 份.
15.如图,在楼顶点A处观察旗杆CD测得旗杆顶部的仰角为30°,旗杆底部D的俯角为45°.已知楼高m,则旗杆CD的高度为 .(结果保留根号)
16.如图,在矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连接EF.已知AB=6,BC=8,则EF的长为 .
三、解答题(本大题共6小题,共56分。)
17.选择适当方法解下列方程:
(1);
(2).
18.某商场将每件进价为160元的某种商品原来按每件200元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降低1元,其销量可增加5件.
(1)求商场经营该商品原来一天可获利润多少元;
(2)若商场经营该商品一天要获利润4320元,则每件商品应降价多少元.
19.为落实“双减”政策.优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟)按照完成时间分成五组:A组.“”,B组.“”,C组.“”,D组.“”,E组“”,将收集的数据整理后,绘制成如图两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)这次调查的总人数是_______人,请补全条形统计图;
(2)在扇形统计图中,B组的圆心角是________度;
(3)若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.
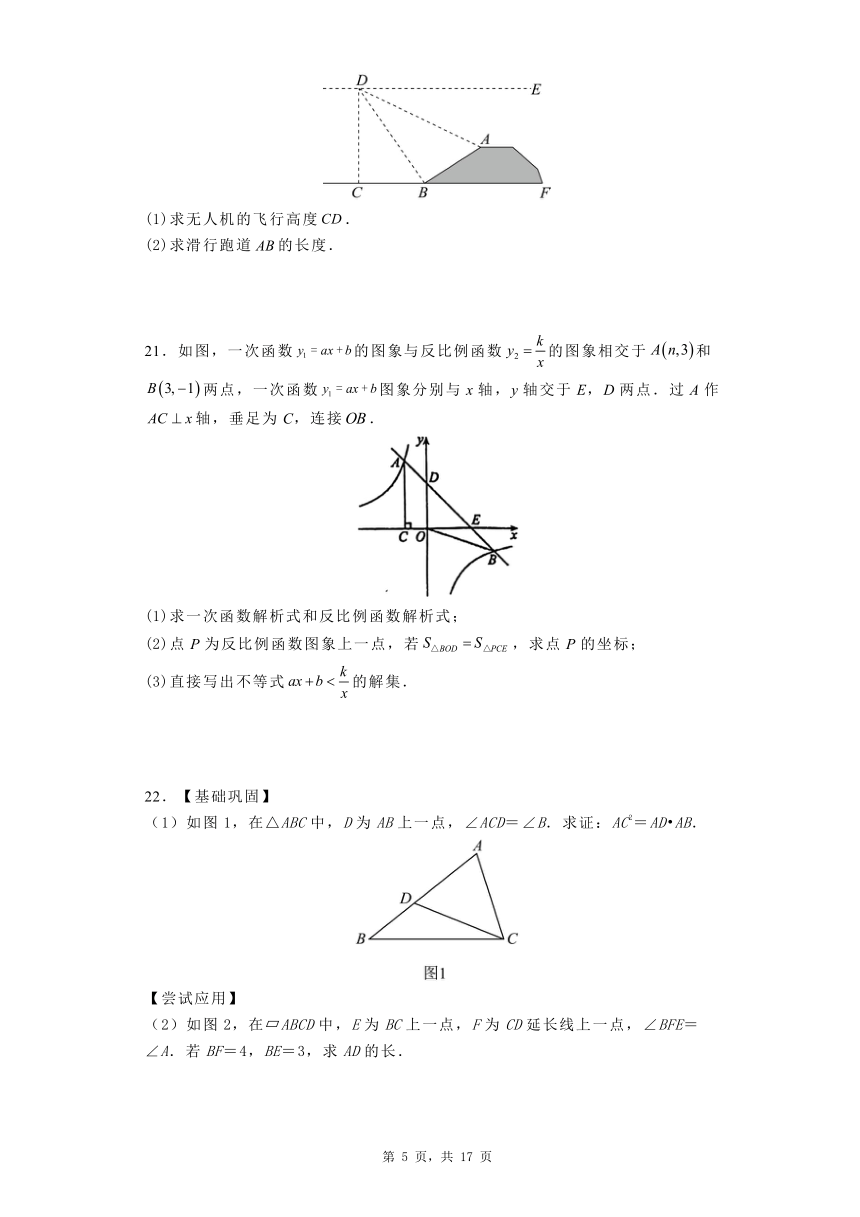
20.新元学校科技社团赵翔同学借助无人机,测量坡角为的滑行跑道斜坡部分的长度.如图所示,水平飞行的无人机在点处测得跑道斜坡的顶端处的俯角,底端点B处的俯角,点C,B,F在同一条水平直线上,米.(所有计算结果精确到1米.参考数据:,,..,,,)
(1)求无人机的飞行高度.
(2)求滑行跑道的长度.
21.如图,一次函数的图象与反比例函数的图象相交于和两点,一次函数图象分别与x轴,y轴交于E,D两点.过A作轴,垂足为C,连接.
(1)求一次函数解析式和反比例函数解析式;
(2)点P为反比例函数图象上一点,若,求点P的坐标;
(3)直接写出不等式的解集.
22.【基础巩固】
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD AB.
【尝试应用】
(2)如图2,在 ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
【拓展提高】
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=∠BAD,AE=2,DF=5,求菱形ABCD的边长.
参考答案
1.【答案】B
【分析】此题考查了反比例函数的定义,形如的函数叫做反比例函数,据此即可求解
【详解】解:由反比例函数的定义可知,B选项符合题意;
故此题答案为B
2.【答案】B
【分析】
结合一次函数与反比例函数的图象,逐项判断即可得.
【详解】解:A、当时,,则此项错误,不符合题意;
B、当时,,则此项正确,符合题意;
C、当时,,则此项错误,不符合题意;
D、当时,,则此项错误,不符合题意;
故此题答案为B.
【关键点拨】此题考查了一次函数与反比例函数的图象,熟练掌握函数图象法是解题关键.
3.【答案】B
【分析】利用根与系数的关系得到,然后利用整体代入的方法计算的值.
【详解】解:根据题意得,
所以.
故选:B.
【关键点拨】本题考查了根与系数的关系:若,是一元二次方程的两根时,.
4.【答案】C
【详解】【分析】根据折线统计图得出两人射击成绩,再计算出两人成绩的方差,据此即可作出判断.
【详解】李飞的成绩为5、8、9、7、8、9、10、8、9、7,
则李飞成绩的平均数为=8,
所以李飞成绩的方差为×[(5﹣8)2+2×(7﹣8)2+3×(8﹣8)2+3×(9﹣8)2+(10﹣8)2]=1.8;
刘亮的成绩为7、8、8、9、7、8、8、9、7、9,
则刘亮成绩的平均数为=8,
∴刘亮成绩的方差为×[3×(7﹣8)2+4×(8﹣8)2+3×(9﹣8)2]=0.6,
∵0.6<1.8,
∴应推荐刘亮,
故选C.
【关键点拨】本题主要考查折线统计图与方差,根据折线统计图得出解题所需数据、熟练应用平均数及方差的计算公式进行求解是解题的关键.
5.【答案】D
【分析】此题主要考查比例的性质,根据比例的性质求解即可.
【详解】解:∵,
∴,
故此题答案为D.
6.【答案】D
【分析】本题考查位似变换.解题的关键是掌握位似图形就是特殊的相似图形,位似比等于相似比,利用相似三角形的性质即可求解.
【详解】解:∵与是位似图形,位似比为,,
∴,
∴,
∴,
∴.
故选:D.
7.【答案】C
【分析】由cosA=,知道∠A=60°,得到∠B的度数即可求得答案.
【详解】解:∵∠C=90°,cosA=,
∴∠A=60°,得∠B=30°,所以tanB=tan30°= .
故选:C.
【关键点拨】考查了特殊角的锐角三角函数值,解题的关键是正确识记30°角的正切值.
8.【答案】C
【分析】
如图,取格点D,连接,,则B在上,由,,,证明,可得.
【详解】解:如图,取格点D,连接,,则B在上,
∵,,,
∴,,,
∴,
∴;
故选C
【关键点拨】本题考查的是坐标与图形,等腰直角三角形的判定与性质,特殊角的三角函数值,作出合适的辅助线构建直角三角形是解本题的关键.
9.【答案】B
【分析】解:设的长为,则,根据面积为列出方程即可.
【详解】解:设的长为,则,根据题意得:
,故B正确.
故此题答案为B.
【关键点拨】此题主要考查了一元二次方程的应用,解题的关键是根据题中等量关系,列出方程.
10.【答案】A
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入(x>0),求出k的值即可.
【详解】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=5,OC=3,
∴DA=AC,DB=OB,AC=OB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=5,OC=3,
∴EF=DF=OA=,AF=AB=,5+=,
∴点E坐标为:(,).
∵反比例函数y=(x>0)的图象经过点E,
∴k=,
故此题答案为:A.
【关键点拨】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
11.【答案】
【分析】
根据反比例函数自变量取值范围计算即可;
【详解】
函数中,自变量x的取值范围是.
故答案为:.
【点睛】
本题主要考查了反比例函数自变量取值范围,准确计算是解题的关键.
12.【答案】
【分析】
将代入,方程,解关于一元一次方程,即可求解,
此题考查了一元二次方程的解,解题的关键是:掌握方程的解的定义.
【详解】解:将,代入,得:,解得:,
故此题答案为:.
13.【答案】
【分析】此题考查的知识点是平行线分线段成比例定理,解题关键是熟练掌握平行线分线段成比例定理.
根据平行线分线段成比例定理得出比例式,带入即可求解.
【详解】解:,,
,
,
,
.
故此题答案为:.
14.【答案】120
【分析】
本题主要考查了扇形统计图和条形统计图中用样本估计总体,先根据等级C的占比和份数求出样本总量,进而求出等级A的占比,再用A的占比估计总体即可.
【详解】解:
,
则等级为的作品约有120份.
故答案为:120.
15.【答案】
【分析】过点A作AE⊥CD于点E,由平行线的性质可知∠ADB=∠EAD=45°,故可得出AB=BD=9m,再根据正方形的判定定理得出四边形ABDE是正方形,故可得出AE=BD,由锐角三角函数的定义求出CE的长,进而可得出结论.
【详解】如图,过点A作AE⊥CD于点E,
∵AE∥BD,
∴∠ADB=∠EAD=45°,
∴AB=BD=9m.
∵AB⊥BD,ED⊥BD,AE⊥CD,AB=BD,
∴四边形ABDE是正方形,
∴AE=BD=AB=DE=9m.
在Rt△ACE中,
∵∠CAE=30°,
∴CE=AE tan30°=9×=3,
∴CD=CE+DE=(3+9)m.
故答案为.
【关键点拨】本题考查的是解直角三角形的应用 仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.
16.【答案】
【分析】根据勾股定理求出BD,根据折叠的性质得到AE=EM,CF=NF,证明△EDM∽△BDA,根据相似三角形的性质求出DE,同理出去DF,根据勾股定理计算,得到答案.
【详解】解:∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠A=∠C=∠EDF=90°,
∴
∵将矩形ABCD沿BE所在直线折叠,使点A落在BD上的点M处,
∴AE=EM,∠A=∠BME=90°,
∴∠EMD=90°,
∵∠EDM=∠ADB,
∴△EDM∽△BDA,
∴,
设DE=x,则AE=EM=8﹣x,
∴
解得,x=5,即DE=5,
同理,△DNF∽△DCB,
∴,
设DF=y,则CF=NF=6﹣y,
∴,
解得,y=,即DF=,
∴,
故答案为:.
【关键点拨】本题主要考查了矩形的性质,折叠的性质,相似三角形的性质与判定,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
17.【答案】(1),;
(2)
【分析】(1)利用公式法解一元二次方程即可;
(2)利用因式分解法解一元二次方程即可.
【详解】(1)解:,
,
∴,
解得,,;
(2)解:,
,
∴,
解得,.
【方法总结】
用因式分解法解一元二次方程的一般步骤:①移项:将方程化为一般形式;②分解:将方程的左边分解为两个一次式的乘积;③转化:令每个一次式分别为0,得到两个一元一次方程;④求解:解这两个一元一次方程,它们的解就是一元二次方程的解.
18.【答案】(1)元;
(2)每件商品应降价4元或16元
【分析】(1)根据总利润=单件利润×销量即可列式计算;
(2)分别表示出销量和单件的利润即可表示出总利润,从而列出方程求解.
【详解】(1)解:原来一天可获利润是元;
(2)解:设每件商品应降价x元,
依题意得,
解得.
∴每件商品应降价4元或16元.
【关键点拨】此题考查了一元二次方程的应用,属于基础题型.解题的关键是能够表示出销量和单件的利润,难度不大.
19.【答案】(1)100,见解析
(2)72
(3)1710人
【分析】(1)根据C组人数及所占比例得出总人数,确定D组的人数即可补全统计图;
(2)用360度乘以B组人数所占的比例即可;
(3)总人数乘以不超过90分钟学生的比例即可得出结果.
【详解】(1)解:人,
∴D组的人数为: ,
补全的条形统计图如下图所示:
(2),
故此题答案为:;
(3) (人),
答:估计该校每天完成书面作业不超过90分钟的学生有1710人.
【关键点拨】题目主要考查扇形统计图与条形统计图,用样本估计总体及求扇形的圆心角等,理解题意,根据扇形统计图与条形统计图获取相关信息是解题关键.
20.【答案】(1)米
(2)30米
【分析】(1)在中根据正切求解即可;
(2)先在中根据余弦求出,然后证明为直角三角形,即可求出AB的值.
【详解】(1)解∶由题意知,,,
则,
在中,,,
∴(米),
答:无人机的飞行高度为米;
(2)解:在中,,,
∴(米),
∵,,
∴,
又∵,,
∴,
∴(米),
滑行跑道的长度30米.
【关键点拨】本题考查解直角三角形、仰角俯角等知识,判断为直角三角形是第(2)问的关键.
21.【答案】(1),
(2)或
(3)或
【分析】此题考查一次函数和反比例函数图象及性质.
(1)将点代入可求出反比例函数解析式,再将代入求出的反比例函数解析式可得,再将和代入可求出一次函数解析式;
(2)令一次函数中分别求出点坐标,再设,再利用三角形面积公式即可求出此题答案;
(3)观察图象即可得到此题答案.
【详解】(1)解:根据题意:将点代入中,得:,,
∴反比例函数解析式:,
再将代入中,得:,
∴,
将和代入中,得:
,解得:,
∴一次函数解析式:;
(2)解:由(1)知:,
∴令,则,令,则,
∴,即,,即:,
∴,
设,
∴,
∴,
∵,
∴,即:,解得:,
∴或.
(3)解:∵,
∴在图象中找出一次函数比反比例函数低的部分,
∴或.
22.【答案】(1)见解析;(2)AD=;(3)5﹣2
【分析】(1)根据题意证明△ADC∽△ACB,即可得到结论;
(2)根据现有条件推出△BFE∽△BCF,再根据相似三角形的性质推断,即可得到答案;
(3)如图,分别延长EF,DC相交于点G,先证明四边形AEGC为平行四边形,再证△EDF∽△EGD,可得,根据EG=AC=2EF,可得DE=EF,再根据,可推出DG=DF=5,即可求出答案.
【详解】解:(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴,
∴AC2=AD AB;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵∠BFE=∠A,
∴∠BFE=∠C,
又∵∠FBE=∠CBF,
∴△BFE∽△BCF,
∴,
∴BF2=BE BC,
∴BC===,
∴AD=;
(3)如图,分别延长EF,DC相交于点G,
∵四边形ABCD是菱形,
∴AB∥DC,∠BAC=∠BAD,
∵AC∥EF,
∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,
∵∠EDF=∠BAD,
∴∠EDF=∠BAC,
∴∠EDF=∠G,
又∵∠DEF=∠GED,
∴△EDF∽△EGD,
∴,
∴DE2=EF EG,
又∵EG=AC=2EF,
∴DE2=2EF2,
∴DE=EF,
又∵,
∴DG=DF=5,
∴DC=DG﹣CG=5﹣2.
【关键点拨】此题考查了相似三角形的性质和判定,菱形的性质,平行四边形的性质和证明,证明三角形相似是解题关键.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.下列关系式中,是x的反比例函数的是( )
A. B. C. D.
2.如图,在直角坐标系中,一次函数与反比例函数的图象交于A,B两点,下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
3.已知,是一元二次方程的两个根,则的值为( )
A. B. C. D.
4.根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A.李飞或刘亮 B.李飞 C.刘亮 D.无法确定
5.若,则的值为( )
A. B. C. D.
6.如图,与是位似图形,是位似中心,位似比为,若,则的长为( )
A. B. C. D.
7.在Rt△ABC中,∠C=90°,cosA=,则tanB等于( )
A. B. C. D.
8.如图,在平面直角坐标系中,有三点,,,则( )
A. B. C. D.
9.如图,用长为的栅栏围成一个面积为的矩形花圃.为方便进出,在边上留有一个宽的小门.设的长为,根据题意可得方程( )
A. B.
C. D.
10.如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且,,反比例函数的图象经过点E,若,,则值是( )
A. B.15 C. D.12
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数中自变量的取值范围是 .
12.已知关于的方程的一个根是,则 .
13.如图,已知,若,.则的长为 .
14.根据《山西省教育厅关于组织参加第五届中华经典诵写讲大赛的通知》,某校组织了“笔墨中国”的汉字书写征文大赛,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两副不完整的统计图.若该校共征集到400份作品,请估计等级为的作品约有 份.
15.如图,在楼顶点A处观察旗杆CD测得旗杆顶部的仰角为30°,旗杆底部D的俯角为45°.已知楼高m,则旗杆CD的高度为 .(结果保留根号)
16.如图,在矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连接EF.已知AB=6,BC=8,则EF的长为 .
三、解答题(本大题共6小题,共56分。)
17.选择适当方法解下列方程:
(1);
(2).
18.某商场将每件进价为160元的某种商品原来按每件200元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降低1元,其销量可增加5件.
(1)求商场经营该商品原来一天可获利润多少元;
(2)若商场经营该商品一天要获利润4320元,则每件商品应降价多少元.
19.为落实“双减”政策.优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟)按照完成时间分成五组:A组.“”,B组.“”,C组.“”,D组.“”,E组“”,将收集的数据整理后,绘制成如图两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)这次调查的总人数是_______人,请补全条形统计图;
(2)在扇形统计图中,B组的圆心角是________度;
(3)若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.
20.新元学校科技社团赵翔同学借助无人机,测量坡角为的滑行跑道斜坡部分的长度.如图所示,水平飞行的无人机在点处测得跑道斜坡的顶端处的俯角,底端点B处的俯角,点C,B,F在同一条水平直线上,米.(所有计算结果精确到1米.参考数据:,,..,,,)
(1)求无人机的飞行高度.
(2)求滑行跑道的长度.
21.如图,一次函数的图象与反比例函数的图象相交于和两点,一次函数图象分别与x轴,y轴交于E,D两点.过A作轴,垂足为C,连接.
(1)求一次函数解析式和反比例函数解析式;
(2)点P为反比例函数图象上一点,若,求点P的坐标;
(3)直接写出不等式的解集.
22.【基础巩固】
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD AB.
【尝试应用】
(2)如图2,在 ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
【拓展提高】
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=∠BAD,AE=2,DF=5,求菱形ABCD的边长.
参考答案
1.【答案】B
【分析】此题考查了反比例函数的定义,形如的函数叫做反比例函数,据此即可求解
【详解】解:由反比例函数的定义可知,B选项符合题意;
故此题答案为B
2.【答案】B
【分析】
结合一次函数与反比例函数的图象,逐项判断即可得.
【详解】解:A、当时,,则此项错误,不符合题意;
B、当时,,则此项正确,符合题意;
C、当时,,则此项错误,不符合题意;
D、当时,,则此项错误,不符合题意;
故此题答案为B.
【关键点拨】此题考查了一次函数与反比例函数的图象,熟练掌握函数图象法是解题关键.
3.【答案】B
【分析】利用根与系数的关系得到,然后利用整体代入的方法计算的值.
【详解】解:根据题意得,
所以.
故选:B.
【关键点拨】本题考查了根与系数的关系:若,是一元二次方程的两根时,.
4.【答案】C
【详解】【分析】根据折线统计图得出两人射击成绩,再计算出两人成绩的方差,据此即可作出判断.
【详解】李飞的成绩为5、8、9、7、8、9、10、8、9、7,
则李飞成绩的平均数为=8,
所以李飞成绩的方差为×[(5﹣8)2+2×(7﹣8)2+3×(8﹣8)2+3×(9﹣8)2+(10﹣8)2]=1.8;
刘亮的成绩为7、8、8、9、7、8、8、9、7、9,
则刘亮成绩的平均数为=8,
∴刘亮成绩的方差为×[3×(7﹣8)2+4×(8﹣8)2+3×(9﹣8)2]=0.6,
∵0.6<1.8,
∴应推荐刘亮,
故选C.
【关键点拨】本题主要考查折线统计图与方差,根据折线统计图得出解题所需数据、熟练应用平均数及方差的计算公式进行求解是解题的关键.
5.【答案】D
【分析】此题主要考查比例的性质,根据比例的性质求解即可.
【详解】解:∵,
∴,
故此题答案为D.
6.【答案】D
【分析】本题考查位似变换.解题的关键是掌握位似图形就是特殊的相似图形,位似比等于相似比,利用相似三角形的性质即可求解.
【详解】解:∵与是位似图形,位似比为,,
∴,
∴,
∴,
∴.
故选:D.
7.【答案】C
【分析】由cosA=,知道∠A=60°,得到∠B的度数即可求得答案.
【详解】解:∵∠C=90°,cosA=,
∴∠A=60°,得∠B=30°,所以tanB=tan30°= .
故选:C.
【关键点拨】考查了特殊角的锐角三角函数值,解题的关键是正确识记30°角的正切值.
8.【答案】C
【分析】
如图,取格点D,连接,,则B在上,由,,,证明,可得.
【详解】解:如图,取格点D,连接,,则B在上,
∵,,,
∴,,,
∴,
∴;
故选C
【关键点拨】本题考查的是坐标与图形,等腰直角三角形的判定与性质,特殊角的三角函数值,作出合适的辅助线构建直角三角形是解本题的关键.
9.【答案】B
【分析】解:设的长为,则,根据面积为列出方程即可.
【详解】解:设的长为,则,根据题意得:
,故B正确.
故此题答案为B.
【关键点拨】此题主要考查了一元二次方程的应用,解题的关键是根据题中等量关系,列出方程.
10.【答案】A
【分析】连接DE,交AB于F,先证明四边形AEBD是平行四边形,再由矩形的性质得出DA=DB,证出四边形AEBD是菱形,由菱形的性质得出AB与DE互相垂直平分,求出EF、AF,得出点E的坐标;把点E坐标代入(x>0),求出k的值即可.
【详解】解:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,OA=5,OC=3,
∴DA=AC,DB=OB,AC=OB,AB=OC=3,
∴DA=DB,
∴四边形AEBD是菱形;
连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=5,OC=3,
∴EF=DF=OA=,AF=AB=,5+=,
∴点E坐标为:(,).
∵反比例函数y=(x>0)的图象经过点E,
∴k=,
故此题答案为:A.
【关键点拨】本题考查了平行四边形的判定、菱形的判定、矩形的性质、坐标与图形特征以及反比例函数解析式的求法;本题综合性强,有一定难度.
11.【答案】
【分析】
根据反比例函数自变量取值范围计算即可;
【详解】
函数中,自变量x的取值范围是.
故答案为:.
【点睛】
本题主要考查了反比例函数自变量取值范围,准确计算是解题的关键.
12.【答案】
【分析】
将代入,方程,解关于一元一次方程,即可求解,
此题考查了一元二次方程的解,解题的关键是:掌握方程的解的定义.
【详解】解:将,代入,得:,解得:,
故此题答案为:.
13.【答案】
【分析】此题考查的知识点是平行线分线段成比例定理,解题关键是熟练掌握平行线分线段成比例定理.
根据平行线分线段成比例定理得出比例式,带入即可求解.
【详解】解:,,
,
,
,
.
故此题答案为:.
14.【答案】120
【分析】
本题主要考查了扇形统计图和条形统计图中用样本估计总体,先根据等级C的占比和份数求出样本总量,进而求出等级A的占比,再用A的占比估计总体即可.
【详解】解:
,
则等级为的作品约有120份.
故答案为:120.
15.【答案】
【分析】过点A作AE⊥CD于点E,由平行线的性质可知∠ADB=∠EAD=45°,故可得出AB=BD=9m,再根据正方形的判定定理得出四边形ABDE是正方形,故可得出AE=BD,由锐角三角函数的定义求出CE的长,进而可得出结论.
【详解】如图,过点A作AE⊥CD于点E,
∵AE∥BD,
∴∠ADB=∠EAD=45°,
∴AB=BD=9m.
∵AB⊥BD,ED⊥BD,AE⊥CD,AB=BD,
∴四边形ABDE是正方形,
∴AE=BD=AB=DE=9m.
在Rt△ACE中,
∵∠CAE=30°,
∴CE=AE tan30°=9×=3,
∴CD=CE+DE=(3+9)m.
故答案为.
【关键点拨】本题考查的是解直角三角形的应用 仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.
16.【答案】
【分析】根据勾股定理求出BD,根据折叠的性质得到AE=EM,CF=NF,证明△EDM∽△BDA,根据相似三角形的性质求出DE,同理出去DF,根据勾股定理计算,得到答案.
【详解】解:∵四边形ABCD是矩形,
∴AB=CD=6,AD=BC=8,∠A=∠C=∠EDF=90°,
∴
∵将矩形ABCD沿BE所在直线折叠,使点A落在BD上的点M处,
∴AE=EM,∠A=∠BME=90°,
∴∠EMD=90°,
∵∠EDM=∠ADB,
∴△EDM∽△BDA,
∴,
设DE=x,则AE=EM=8﹣x,
∴
解得,x=5,即DE=5,
同理,△DNF∽△DCB,
∴,
设DF=y,则CF=NF=6﹣y,
∴,
解得,y=,即DF=,
∴,
故答案为:.
【关键点拨】本题主要考查了矩形的性质,折叠的性质,相似三角形的性质与判定,勾股定理,解题的关键在于能够熟练掌握相关知识进行求解.
17.【答案】(1),;
(2)
【分析】(1)利用公式法解一元二次方程即可;
(2)利用因式分解法解一元二次方程即可.
【详解】(1)解:,
,
∴,
解得,,;
(2)解:,
,
∴,
解得,.
【方法总结】
用因式分解法解一元二次方程的一般步骤:①移项:将方程化为一般形式;②分解:将方程的左边分解为两个一次式的乘积;③转化:令每个一次式分别为0,得到两个一元一次方程;④求解:解这两个一元一次方程,它们的解就是一元二次方程的解.
18.【答案】(1)元;
(2)每件商品应降价4元或16元
【分析】(1)根据总利润=单件利润×销量即可列式计算;
(2)分别表示出销量和单件的利润即可表示出总利润,从而列出方程求解.
【详解】(1)解:原来一天可获利润是元;
(2)解:设每件商品应降价x元,
依题意得,
解得.
∴每件商品应降价4元或16元.
【关键点拨】此题考查了一元二次方程的应用,属于基础题型.解题的关键是能够表示出销量和单件的利润,难度不大.
19.【答案】(1)100,见解析
(2)72
(3)1710人
【分析】(1)根据C组人数及所占比例得出总人数,确定D组的人数即可补全统计图;
(2)用360度乘以B组人数所占的比例即可;
(3)总人数乘以不超过90分钟学生的比例即可得出结果.
【详解】(1)解:人,
∴D组的人数为: ,
补全的条形统计图如下图所示:
(2),
故此题答案为:;
(3) (人),
答:估计该校每天完成书面作业不超过90分钟的学生有1710人.
【关键点拨】题目主要考查扇形统计图与条形统计图,用样本估计总体及求扇形的圆心角等,理解题意,根据扇形统计图与条形统计图获取相关信息是解题关键.
20.【答案】(1)米
(2)30米
【分析】(1)在中根据正切求解即可;
(2)先在中根据余弦求出,然后证明为直角三角形,即可求出AB的值.
【详解】(1)解∶由题意知,,,
则,
在中,,,
∴(米),
答:无人机的飞行高度为米;
(2)解:在中,,,
∴(米),
∵,,
∴,
又∵,,
∴,
∴(米),
滑行跑道的长度30米.
【关键点拨】本题考查解直角三角形、仰角俯角等知识,判断为直角三角形是第(2)问的关键.
21.【答案】(1),
(2)或
(3)或
【分析】此题考查一次函数和反比例函数图象及性质.
(1)将点代入可求出反比例函数解析式,再将代入求出的反比例函数解析式可得,再将和代入可求出一次函数解析式;
(2)令一次函数中分别求出点坐标,再设,再利用三角形面积公式即可求出此题答案;
(3)观察图象即可得到此题答案.
【详解】(1)解:根据题意:将点代入中,得:,,
∴反比例函数解析式:,
再将代入中,得:,
∴,
将和代入中,得:
,解得:,
∴一次函数解析式:;
(2)解:由(1)知:,
∴令,则,令,则,
∴,即,,即:,
∴,
设,
∴,
∴,
∵,
∴,即:,解得:,
∴或.
(3)解:∵,
∴在图象中找出一次函数比反比例函数低的部分,
∴或.
22.【答案】(1)见解析;(2)AD=;(3)5﹣2
【分析】(1)根据题意证明△ADC∽△ACB,即可得到结论;
(2)根据现有条件推出△BFE∽△BCF,再根据相似三角形的性质推断,即可得到答案;
(3)如图,分别延长EF,DC相交于点G,先证明四边形AEGC为平行四边形,再证△EDF∽△EGD,可得,根据EG=AC=2EF,可得DE=EF,再根据,可推出DG=DF=5,即可求出答案.
【详解】解:(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴,
∴AC2=AD AB;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵∠BFE=∠A,
∴∠BFE=∠C,
又∵∠FBE=∠CBF,
∴△BFE∽△BCF,
∴,
∴BF2=BE BC,
∴BC===,
∴AD=;
(3)如图,分别延长EF,DC相交于点G,
∵四边形ABCD是菱形,
∴AB∥DC,∠BAC=∠BAD,
∵AC∥EF,
∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,
∵∠EDF=∠BAD,
∴∠EDF=∠BAC,
∴∠EDF=∠G,
又∵∠DEF=∠GED,
∴△EDF∽△EGD,
∴,
∴DE2=EF EG,
又∵EG=AC=2EF,
∴DE2=2EF2,
∴DE=EF,
又∵,
∴DG=DF=5,
∴DC=DG﹣CG=5﹣2.
【关键点拨】此题考查了相似三角形的性质和判定,菱形的性质,平行四边形的性质和证明,证明三角形相似是解题关键.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
同课章节目录
