2023-2024学年湖南省益阳市部分学校八年级上册数学期末联考试题卷(含解析)
文档属性
| 名称 | 2023-2024学年湖南省益阳市部分学校八年级上册数学期末联考试题卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 814.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-16 13:36:24 | ||
图片预览




文档简介
八年级数学(问卷)
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.2的平方根是( )
A. B.2 C. D.
2.下列分式是最简分式的是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B.
C. D.
4.估算的结果( )
A.在6和7之间 B.在7和8之间 C.在8和9之间 D.在9和10之间
5.若等腰三角形有一个内角为,则这个等腰三角形的底角是( )
A. B. C. D.
6.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃, 那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
7.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
8.有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )
A. B. C. D.
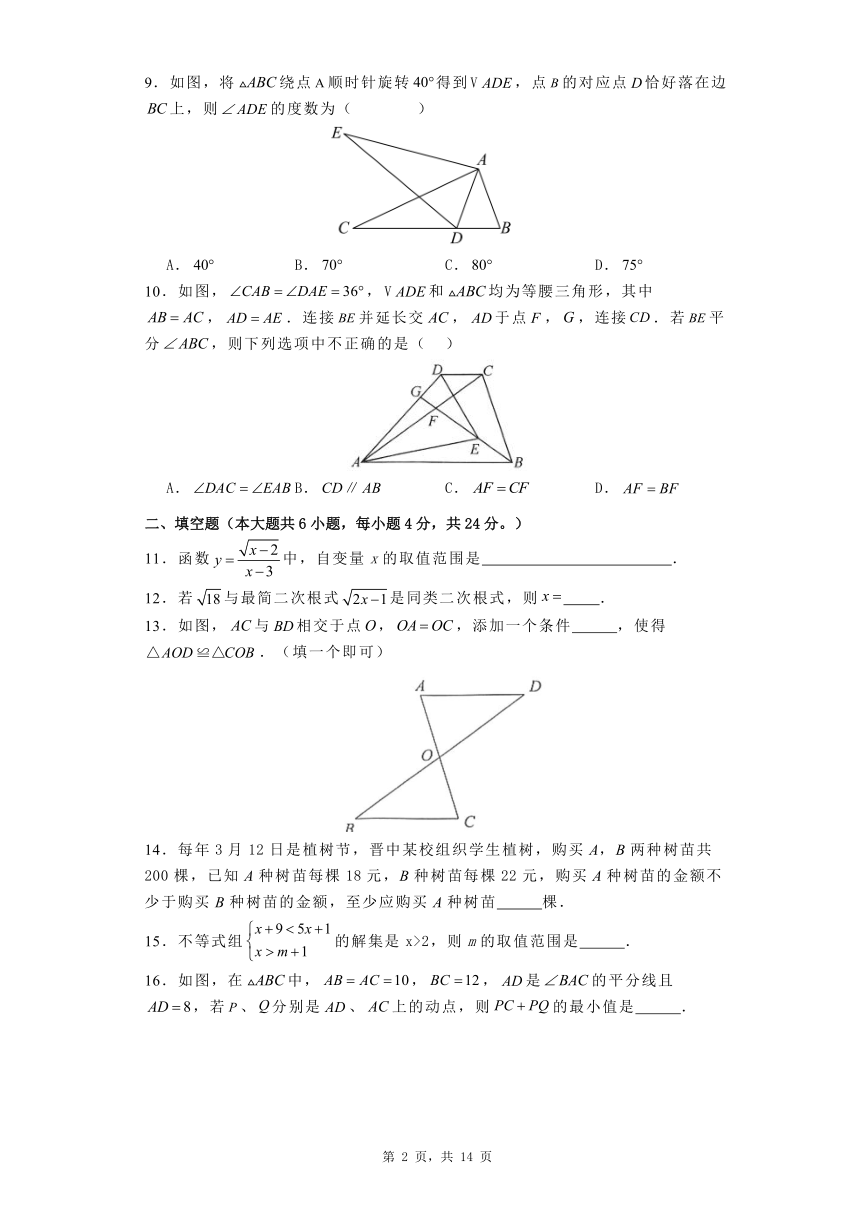
9.如图,将绕点顺时针旋转得到,点的对应点恰好落在边上,则的度数为( )
A. B. C. D.
10.如图,,和均为等腰三角形,其中,.连接并延长交,于点,,连接.若平分,则下列选项中不正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数中,自变量x的取值范围是 .
12.若与最简二次根式是同类二次根式,则 .
13.如图,与相交于点,,添加一个条件 ,使得.(填一个即可)
14.每年3月12日是植树节,晋中某校组织学生植树,购买A,B两种树苗共200棵,已知A种树苗每棵18元,B种树苗每棵22元,购买A种树苗的金额不少于购买B种树苗的金额,至少应购买A种树苗 棵.
15.不等式组的解集是x>2,则m的取值范围是 .
16.如图,在中,,,是的平分线且,若、分别是、上的动点,则的最小值是 .
三、解答题(本大题共6小题,共56分。)
17.先化简,再求值:,其中从,2,3中取一个你认为合适的数代入求值.
18.如图,在和中,,,,点在上.
(1)证明:;
(2)求的度数.
19.为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(1)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?
20.某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)求矩形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?
21.某杨梅采摘园收费信息如下表:
成人票 儿童票 带出杨梅价格
不超过人 超过人 元/人 元/斤
元/人 每增加1人,人均票价下降1元,但不低于儿童票价
(1)某公司员工(均为成人)在该杨梅采摘园组织团建活动,共支付票价元,求这次参加团建的共多少人?
(2)某社团共人去该采摘园进行综合实践活动,购买了张儿童票,其余均为成人票,总费用不超过元,求本次活动他们最多共带出杨梅多少斤?
22.如图,在中,,点是上一动点,点在的延长线上,且,平分交于,连接.
(1)如图1,求证:;
(2)如图2,时,求证:;
(3)如图3,当时,过点A作的垂线,过点作的平行线,两直线l,n相交于,连接.当取得最大值时,请直接写出此时的值.
参考答案
1.【答案】C
【分析】直接利用平方根的定义得出答案.
【详解】解:2的平方根是:.
故选:C.
【关键点拨】此题主要考查了平方根的定义,正确把握定义是解题关键.
2.【答案】A
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
【详解】解:A、的分子分母中不含有公因式,故此选项符合题意;
B、,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项不符合题意;
故此题答案为A.
【关键点拨】此题考查了最简分式,熟练掌握最简分式的定义是解此题的关键.
3.【答案】C
【详解】解:、,该选项错误,不合题意;
、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
故此题答案为.
4.【答案】D
【详解】解:,
∵,
∴;
故此题答案为D.
5.【答案】C
【分析】先判断出的内角是这个等腰三角形的顶角,再根据等腰三角形的定义求解即可得.
【详解】解:等腰三角形有一个内角为,
∴这个等腰三角形的底角是,
故此题答案为C.
【关键点拨】此题考查了等腰三角形的定义,三角形内角和定理,解题的关键是熟练掌握等腰三角形的两个底角相等.
6.【答案】A
【分析】此题考查了全等三角形的判定方法的开放性的题,根据全等三角形的判定方法逐项判断即可,熟练掌握全等三角形的判定方法是解此题的关键.
【详解】解:A、保留了两个角和它们的夹边,能确定三角形的形状和大小,符合要求;
B、不能确定三角形的形状和大小,不符合要求;
C、仅保留了三角形的一个角,不能确定三角形的形状和大小,不符合要求;
D、带①去和带②去,可以确定三角形的形状和大小,但是不是最省事的办法,不符合要求;
故此题答案为A.
7.【答案】D
【分析】根据不等式的性质,求出不等式的解集即可.
【详解】∵
∴x>-1
在数轴上表示D选项是正确的;
故此题答案为:D
【关键点拨】此题主要考查了解不等式并把解集在数轴上表示,熟练的掌握不等式的性质,会求不等式的解集,是解题的关键.注意:“>、<”在数轴上是空心小圆圈,“≥、≤”在数轴上是实心小圆点.
8.【答案】C
【详解】根据关键描述语:“有两块面积相同的试验田”得到等量关系为:第一块的亩数=第二块的亩数,而亩数=总产量÷单产量.设第一块试验田每亩收获蔬菜xkg,则第一块试验田的亩数为: ,第二块试验田的亩数为: .那么所列方程为:=.
故此题答案为C
关键点拨:此题考查了由实际问题抽象出分式方程,抓住关键描述语,找到等量关系是解决问题的关键.此题用到的等量关系为:亩数=总产量÷单产量.
9.【答案】B
【分析】根据旋转的性质得到,,根据等腰三角形的性质得到,求得.
【详解】解:由旋转的性质可知,,,
∴,
∵,
∴,
故此题答案为.
10.【答案】C
【分析】此题根据,得到,即可判断A项,根据题意证明,由等腰三角形性质得到,由角平分线性质得到,推出,即可判断B、D项,根据题意继续推出,即可判断C项.
【详解】解:,
,
即,
A项正确,不符合题意.
,,
,
,
又,
,
平分,
,
,
,,
B、D项正确,不符合题意.
,,
,
,
,
,
C项错误,符合题意.
故此题答案为C.
【关键点拨】此题考查了全等三角形的性质和判定、角平分线的性质、等腰三角形性质、平行的判定定理、熟练掌握相关性质并灵活运用,即可解题.
11.【答案】且
【分析】根据二次根式有意义的条件和分式有意义的条件进行求解即可.
【详解】解:∵要有意义,
∴,
∴且.
【刷有所得】若二次根式有意义,则被开方数是非负数,再结合分式的分母不等于零即可得出答案.
12.【答案】
【分析】
先把化简,再根据同类二次根式的定义列方程从而解方程可得答案.
【详解】
解: 而与最简二次根式是同类二次根式,
故答案为:
【点睛】
本题考查的是同类二次根式与最简二次根式的定义,以及利用定义求解字母系数的值,理解同类二次根式的定义是解题的关键.
13.【答案】或或或(答案不唯一)
【分析】此题考查了添加条件判定三角形全等,首先根据图形,可知,又由已知,可添加或或或,解题的关键是熟练掌握全等三角形的判定方法及其应用.
【详解】解:∵,,
添加,
∴;
添加,
∴;
添加,
∴;
添加,
∴,,同理,
故此题答案为:或或或(答案不唯一).
14.【答案】110
【分析】设购买A种树苗x棵,则购买B种树苗棵,根据题意列出一元一次不等式,解不等式即可作答.
【详解】设购买A种树苗x棵,则购买B种树苗棵,
根据题意有:,
解得,
即至少应购买A种树苗110棵,
故答案为:110.
【点睛】本题主要考查一元一次不等式的应用,明确题意,列出一元一次不等式,是解答本题的关键.
15.【答案】m≤1
【分析】根据不等式的性质求出不等式的解集,根据不等式组的解集得到2≥m+1,求出即可.
【详解】,
由①得:x>2,
由②得:x>m+1,
∵不等式组的解集是 x>2,
∴2≥m+1,
∴m≤1,
故此题答案为m≤1.
16.【答案】
【分析】此题考查轴对称——最短路线问题、等腰三角形的性质、线段垂直平分线的性质以及三角形的面积,由等腰三角形的三线合一可得出垂直平分,过点作于点,交于点,则此时 取最小值,最小值为的长,在中,利用面积法可求出的长度,此题得解,掌握等腰三角形的性质、线段垂直平分线的性质和最短路径问题的解决方法是解题的关键.
【详解】∵,是的平分线,
∴垂直平分,
∴,
过点作于点,交于点,则此时 取最小值,最小值为的长,如图所示,
∵,
∴,
故此题答案为:.
17.【答案】,-4
【分析】先按照分式运算法则进行化简,再选取数轴代入计算即可.
【详解】解:
=
=
=
当取和2时,分式无意义,故此题答案为;
把代入,原式=.
【关键点拨】此题考查了分式的化简求值,解题关键是熟练运用分式运算法则进行准确计算,代入数值后正确求值.
18.【答案】(1)证明见解析
(2)
【分析】此题考查了三角形全等的判定与性质、等腰三角形的性质,熟练掌握三角形全等的判定与性质是解题关键.
(1)先求出,再根据定理即可得证;
(2)先根据全等三角形的性质可得,再根据等腰三角形的性质求解即可得.
【详解】(1)证明:,
,即,
在和中,
,
.
(2)解:由(1)已证:,
,
.
19.【答案】(1)A,B两种学习用品的单价分别为20元和30元
(2)80
【分析】(1)设A种学习用品的单价为元,则B种学习用品的单价为元,由题意得,然后解分式方程解即可;
(2)设最多购买B型学习用品件,则购买A型学习用品件,由题意得,,解不等式即可.
【详解】(1)解:设A种学习用品的单价为元,则B种学习用品的单价为元
由题意得
去分母得,
移项合并得,
系数化为1得,
经检验,是原分式方程的解
∴元
∴A、B两种学习用品的单价分别为20元和30元.
(2)解:设最多购买B型学习用品件,则购买A型学习用品件
由题意得,
解得
∴最多购买B型学习用品80件.
【关键点拨】此题考查了分式方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式与不等式.
20.【答案】(1)米
(2)336元
【分析】(1)根据长方形ABCD的周长列出算式,再利用二次根式的运算法则计算可得;
(2)先用长方形ABCD的面积减去2个花坛的面积,求出通道的面积,再计算花费.
【详解】(1)解:矩形的长为米,宽为米,
∴矩形的周长为(米).
答:矩形的周长为米.
(2)解:通道的面积为(平方米),
则购买地砖需要花费(元).
答:购买地砖需要花费336元.
【点睛】本题考查二次根式混合运算的实际应用,熟练掌握平方差公式、二次根式运算法则是解题的关键.
21.【答案】(1)
(2)
【分析】本题考查了一元二次方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式、不等式.
(1)设这次参加团建的共人,由题意求得,依题意得,,计算求出满足要求的解即可;
(2)由题意求得,当成人人数大于或等于人时,成人票都是元/人, 由(人),,可得该社团购买的成人票为元/人,设本次活动他们最多共带出杨梅斤,依题意得,,计算求解,然后作答即可.
【详解】(1)解:设这次参加团建的共人,
由题意知,(元),(元),
∵,
∴,
依题意得,,整理得,,
,
∴或,
解得,或(舍去)
∴这次参加团建的共人;
(2)解:∵(人),(人),
∴当成人人数大于或等于人时,成人票都是元/人,
∵(人),,
∴该社团购买的成人票为元/人,
设本次活动他们最多共带出杨梅斤,
依题意得,,
解得,,
∴本次活动他们最多共带出杨梅斤.
22.【答案】(1)证明见解析
(2)证明见解析
(3)
【分析】此题考查了三角形全等的判定和性质、等腰三角形的性质等知识,熟练掌握并灵活运用相关知识点是解题的关键.
(1)利用定理证明三角形全等,根据全等的性质和等腰三角形的性质即可证明;
(2)截取线段从而构造出全等三角形,通过线段转化和等边三角形即可证明;
(3)找出点的轨迹,确定何时最大,通过全等即可求出答案.
【详解】(1)证明:平分
(2)如图,在上截取,连接
由(1)得
是等边三角形
是等边三角形
即
(3)如图,,
点是上一动点,
以为圆心,为半径作
点是上一动点,
则点在上运动,当点到达点时,点到达点,当点到达点时,点到达点,故点在上运动
则当三点共线时,最大
则由题意可得,,,
即此时
如图,延长交于点
由(1)得
由(2)得
.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
一、选择题(本大题共10小题,每小题4分,共40分。每小题只有1个选项符合题意。请将符合题意的选项用2B铅笔填涂在答题卡相应位置)
1.2的平方根是( )
A. B.2 C. D.
2.下列分式是最简分式的是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B.
C. D.
4.估算的结果( )
A.在6和7之间 B.在7和8之间 C.在8和9之间 D.在9和10之间
5.若等腰三角形有一个内角为,则这个等腰三角形的底角是( )
A. B. C. D.
6.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃, 那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
7.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
8.有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )
A. B. C. D.
9.如图,将绕点顺时针旋转得到,点的对应点恰好落在边上,则的度数为( )
A. B. C. D.
10.如图,,和均为等腰三角形,其中,.连接并延长交,于点,,连接.若平分,则下列选项中不正确的是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分。)
11.函数中,自变量x的取值范围是 .
12.若与最简二次根式是同类二次根式,则 .
13.如图,与相交于点,,添加一个条件 ,使得.(填一个即可)
14.每年3月12日是植树节,晋中某校组织学生植树,购买A,B两种树苗共200棵,已知A种树苗每棵18元,B种树苗每棵22元,购买A种树苗的金额不少于购买B种树苗的金额,至少应购买A种树苗 棵.
15.不等式组的解集是x>2,则m的取值范围是 .
16.如图,在中,,,是的平分线且,若、分别是、上的动点,则的最小值是 .
三、解答题(本大题共6小题,共56分。)
17.先化简,再求值:,其中从,2,3中取一个你认为合适的数代入求值.
18.如图,在和中,,,,点在上.
(1)证明:;
(2)求的度数.
19.为支援贫困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(1)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共100件,且总费用不超过2800元,则最多购买B型学习用品多少件?
20.某居民小区有块形状为矩形的绿地,长为米,宽为米,现在要矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为米,宽为米.
(1)求矩形的周长.(结果化为最简二次根式)
(2)除去修建花坛的地方,其它地方全修建成通道,通道上要铺上造价为6元/平方米的地砖,要铺完整个通道,则购买地砖需要花费多少元?
21.某杨梅采摘园收费信息如下表:
成人票 儿童票 带出杨梅价格
不超过人 超过人 元/人 元/斤
元/人 每增加1人,人均票价下降1元,但不低于儿童票价
(1)某公司员工(均为成人)在该杨梅采摘园组织团建活动,共支付票价元,求这次参加团建的共多少人?
(2)某社团共人去该采摘园进行综合实践活动,购买了张儿童票,其余均为成人票,总费用不超过元,求本次活动他们最多共带出杨梅多少斤?
22.如图,在中,,点是上一动点,点在的延长线上,且,平分交于,连接.
(1)如图1,求证:;
(2)如图2,时,求证:;
(3)如图3,当时,过点A作的垂线,过点作的平行线,两直线l,n相交于,连接.当取得最大值时,请直接写出此时的值.
参考答案
1.【答案】C
【分析】直接利用平方根的定义得出答案.
【详解】解:2的平方根是:.
故选:C.
【关键点拨】此题主要考查了平方根的定义,正确把握定义是解题关键.
2.【答案】A
【分析】利用最简分式定义:分子分母没有公因式的分式,判断即可.
【详解】解:A、的分子分母中不含有公因式,故此选项符合题意;
B、,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项不符合题意;
故此题答案为A.
【关键点拨】此题考查了最简分式,熟练掌握最简分式的定义是解此题的关键.
3.【答案】C
【详解】解:、,该选项错误,不合题意;
、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
故此题答案为.
4.【答案】D
【详解】解:,
∵,
∴;
故此题答案为D.
5.【答案】C
【分析】先判断出的内角是这个等腰三角形的顶角,再根据等腰三角形的定义求解即可得.
【详解】解:等腰三角形有一个内角为,
∴这个等腰三角形的底角是,
故此题答案为C.
【关键点拨】此题考查了等腰三角形的定义,三角形内角和定理,解题的关键是熟练掌握等腰三角形的两个底角相等.
6.【答案】A
【分析】此题考查了全等三角形的判定方法的开放性的题,根据全等三角形的判定方法逐项判断即可,熟练掌握全等三角形的判定方法是解此题的关键.
【详解】解:A、保留了两个角和它们的夹边,能确定三角形的形状和大小,符合要求;
B、不能确定三角形的形状和大小,不符合要求;
C、仅保留了三角形的一个角,不能确定三角形的形状和大小,不符合要求;
D、带①去和带②去,可以确定三角形的形状和大小,但是不是最省事的办法,不符合要求;
故此题答案为A.
7.【答案】D
【分析】根据不等式的性质,求出不等式的解集即可.
【详解】∵
∴x>-1
在数轴上表示D选项是正确的;
故此题答案为:D
【关键点拨】此题主要考查了解不等式并把解集在数轴上表示,熟练的掌握不等式的性质,会求不等式的解集,是解题的关键.注意:“>、<”在数轴上是空心小圆圈,“≥、≤”在数轴上是实心小圆点.
8.【答案】C
【详解】根据关键描述语:“有两块面积相同的试验田”得到等量关系为:第一块的亩数=第二块的亩数,而亩数=总产量÷单产量.设第一块试验田每亩收获蔬菜xkg,则第一块试验田的亩数为: ,第二块试验田的亩数为: .那么所列方程为:=.
故此题答案为C
关键点拨:此题考查了由实际问题抽象出分式方程,抓住关键描述语,找到等量关系是解决问题的关键.此题用到的等量关系为:亩数=总产量÷单产量.
9.【答案】B
【分析】根据旋转的性质得到,,根据等腰三角形的性质得到,求得.
【详解】解:由旋转的性质可知,,,
∴,
∵,
∴,
故此题答案为.
10.【答案】C
【分析】此题根据,得到,即可判断A项,根据题意证明,由等腰三角形性质得到,由角平分线性质得到,推出,即可判断B、D项,根据题意继续推出,即可判断C项.
【详解】解:,
,
即,
A项正确,不符合题意.
,,
,
,
又,
,
平分,
,
,
,,
B、D项正确,不符合题意.
,,
,
,
,
,
C项错误,符合题意.
故此题答案为C.
【关键点拨】此题考查了全等三角形的性质和判定、角平分线的性质、等腰三角形性质、平行的判定定理、熟练掌握相关性质并灵活运用,即可解题.
11.【答案】且
【分析】根据二次根式有意义的条件和分式有意义的条件进行求解即可.
【详解】解:∵要有意义,
∴,
∴且.
【刷有所得】若二次根式有意义,则被开方数是非负数,再结合分式的分母不等于零即可得出答案.
12.【答案】
【分析】
先把化简,再根据同类二次根式的定义列方程从而解方程可得答案.
【详解】
解: 而与最简二次根式是同类二次根式,
故答案为:
【点睛】
本题考查的是同类二次根式与最简二次根式的定义,以及利用定义求解字母系数的值,理解同类二次根式的定义是解题的关键.
13.【答案】或或或(答案不唯一)
【分析】此题考查了添加条件判定三角形全等,首先根据图形,可知,又由已知,可添加或或或,解题的关键是熟练掌握全等三角形的判定方法及其应用.
【详解】解:∵,,
添加,
∴;
添加,
∴;
添加,
∴;
添加,
∴,,同理,
故此题答案为:或或或(答案不唯一).
14.【答案】110
【分析】设购买A种树苗x棵,则购买B种树苗棵,根据题意列出一元一次不等式,解不等式即可作答.
【详解】设购买A种树苗x棵,则购买B种树苗棵,
根据题意有:,
解得,
即至少应购买A种树苗110棵,
故答案为:110.
【点睛】本题主要考查一元一次不等式的应用,明确题意,列出一元一次不等式,是解答本题的关键.
15.【答案】m≤1
【分析】根据不等式的性质求出不等式的解集,根据不等式组的解集得到2≥m+1,求出即可.
【详解】,
由①得:x>2,
由②得:x>m+1,
∵不等式组的解集是 x>2,
∴2≥m+1,
∴m≤1,
故此题答案为m≤1.
16.【答案】
【分析】此题考查轴对称——最短路线问题、等腰三角形的性质、线段垂直平分线的性质以及三角形的面积,由等腰三角形的三线合一可得出垂直平分,过点作于点,交于点,则此时 取最小值,最小值为的长,在中,利用面积法可求出的长度,此题得解,掌握等腰三角形的性质、线段垂直平分线的性质和最短路径问题的解决方法是解题的关键.
【详解】∵,是的平分线,
∴垂直平分,
∴,
过点作于点,交于点,则此时 取最小值,最小值为的长,如图所示,
∵,
∴,
故此题答案为:.
17.【答案】,-4
【分析】先按照分式运算法则进行化简,再选取数轴代入计算即可.
【详解】解:
=
=
=
当取和2时,分式无意义,故此题答案为;
把代入,原式=.
【关键点拨】此题考查了分式的化简求值,解题关键是熟练运用分式运算法则进行准确计算,代入数值后正确求值.
18.【答案】(1)证明见解析
(2)
【分析】此题考查了三角形全等的判定与性质、等腰三角形的性质,熟练掌握三角形全等的判定与性质是解题关键.
(1)先求出,再根据定理即可得证;
(2)先根据全等三角形的性质可得,再根据等腰三角形的性质求解即可得.
【详解】(1)证明:,
,即,
在和中,
,
.
(2)解:由(1)已证:,
,
.
19.【答案】(1)A,B两种学习用品的单价分别为20元和30元
(2)80
【分析】(1)设A种学习用品的单价为元,则B种学习用品的单价为元,由题意得,然后解分式方程解即可;
(2)设最多购买B型学习用品件,则购买A型学习用品件,由题意得,,解不等式即可.
【详解】(1)解:设A种学习用品的单价为元,则B种学习用品的单价为元
由题意得
去分母得,
移项合并得,
系数化为1得,
经检验,是原分式方程的解
∴元
∴A、B两种学习用品的单价分别为20元和30元.
(2)解:设最多购买B型学习用品件,则购买A型学习用品件
由题意得,
解得
∴最多购买B型学习用品80件.
【关键点拨】此题考查了分式方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式与不等式.
20.【答案】(1)米
(2)336元
【分析】(1)根据长方形ABCD的周长列出算式,再利用二次根式的运算法则计算可得;
(2)先用长方形ABCD的面积减去2个花坛的面积,求出通道的面积,再计算花费.
【详解】(1)解:矩形的长为米,宽为米,
∴矩形的周长为(米).
答:矩形的周长为米.
(2)解:通道的面积为(平方米),
则购买地砖需要花费(元).
答:购买地砖需要花费336元.
【点睛】本题考查二次根式混合运算的实际应用,熟练掌握平方差公式、二次根式运算法则是解题的关键.
21.【答案】(1)
(2)
【分析】本题考查了一元二次方程的应用,一元一次不等式的应用.解题的关键在于根据题意正确的列等式、不等式.
(1)设这次参加团建的共人,由题意求得,依题意得,,计算求出满足要求的解即可;
(2)由题意求得,当成人人数大于或等于人时,成人票都是元/人, 由(人),,可得该社团购买的成人票为元/人,设本次活动他们最多共带出杨梅斤,依题意得,,计算求解,然后作答即可.
【详解】(1)解:设这次参加团建的共人,
由题意知,(元),(元),
∵,
∴,
依题意得,,整理得,,
,
∴或,
解得,或(舍去)
∴这次参加团建的共人;
(2)解:∵(人),(人),
∴当成人人数大于或等于人时,成人票都是元/人,
∵(人),,
∴该社团购买的成人票为元/人,
设本次活动他们最多共带出杨梅斤,
依题意得,,
解得,,
∴本次活动他们最多共带出杨梅斤.
22.【答案】(1)证明见解析
(2)证明见解析
(3)
【分析】此题考查了三角形全等的判定和性质、等腰三角形的性质等知识,熟练掌握并灵活运用相关知识点是解题的关键.
(1)利用定理证明三角形全等,根据全等的性质和等腰三角形的性质即可证明;
(2)截取线段从而构造出全等三角形,通过线段转化和等边三角形即可证明;
(3)找出点的轨迹,确定何时最大,通过全等即可求出答案.
【详解】(1)证明:平分
(2)如图,在上截取,连接
由(1)得
是等边三角形
是等边三角形
即
(3)如图,,
点是上一动点,
以为圆心,为半径作
点是上一动点,
则点在上运动,当点到达点时,点到达点,当点到达点时,点到达点,故点在上运动
则当三点共线时,最大
则由题意可得,,,
即此时
如图,延长交于点
由(1)得
由(2)得
.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
同课章节目录
